基于優化初始聚類中心的Kmeans聚類算法

摘?要：針對傳統的Kmeans算法運行的結果依賴于初始的聚類數目和聚類中心，本文提出了一種基于優化初始聚類中心的Kmeans算法。該算法通過量化樣本間距離和聚類的緊密性來確定聚類數目K值;根據數據集的分布特征來選取相距較遠的數據作為初始聚類中心，避免了傳統Kmeans算法的聚類數目和聚類中心的隨機選取。UCI機器學習數據庫數據集的實驗證明，本文所提出的改進的聚類算法獲得了良好的聚類效果，同時獲得較高的聚類準確率。

關鍵詞：聚類;Kmeans聚類;聚類數目;初始聚類中心

文獻標識碼：A

在模式識別、數據挖掘和機器學習等領域，聚類算法是很有意義的研究內容[1]。物以類聚，聚類是將數據集中的數據對象按照對象間的相似性劃分成若干個類，使同一類的對象間差別小，而不同類的對象間差別大[2]。

Kmeans聚類算法是經典且應用廣泛的劃分方法之一，具有理論可靠、算法簡單、收斂速度快、能有效處理大數據集等優點[3]。但是傳統的Kmeans算法過度依賴于初始條件。初始聚類數目K值的確定影響了最終的聚類效果和整個算法的收斂速度。假設聚類數目K值已經確定，選取不同的初始聚類中心又會導致不同的聚類結果，隨機選取的初始聚類中心點將會增加最終聚類結果的隨機性和不可靠性。由此可見，對于聚類初始條件優化的研究在Kmeans聚類算法改進中有著重要的地位。國內外諸多學者致力于Kmeans算法初始條件的研究，以改善K均值算法的聚類效果[46]。

本文提出一種基于優化初始聚類中心的Kmeans算法，該算法在聚類數目K值的確定上和初始聚類中心的選取上都做了改進，避免了傳統Kmeans算法的聚類數目和聚類中心的隨機選取。UCI機器學習數據庫數據集的實驗測試證明，本文所提出的算法具有良好的聚類效果，聚類準確率高。

1?Kmeans聚類算法

傳統的Kmeans聚類算法用聚類誤差平方和作為衡量聚類效果的準則函數。傳統Kmeans算法會隨機選擇出K個數據作為最初的聚類中心，然后計算出數據集中剩余數據和各聚類中心的距離，根據距離將其余數據分配到各類中，重新確定各個類簇的新中心點，再分配數據集中樣本到新的聚類中心，再計算各個類的新中心點，再次分配數據集樣本。反復迭代到準則函數收斂為止，也就是聚類中心點不再發生變化。

2?基于優化初始聚類中心的Kmeans聚類算法

2.1?聚類數目K值的確定

聚類算法是通過量化樣本間距離和聚類的緊密性來評價聚類效果的好壞。具體表示為：同一個類內數據間的距離越小越好、不同類間的距離越大越好。本文將同一類簇內的差異值和不同類簇間的差異值的比值定義為評價聚類效果優劣的標準。

將數據集所有的類簇內距離和定義為Ein，表示每個類簇中所包含的數據樣本到各個類中心點間的距離之和。類簇內距離和Ein的計算公式表示為：

其中，n是表示數據集中所有的樣本數量，k表示類的個數，Ci表示第i個類簇，x為第i類中的數據樣本，Zi表示第i個類的中心點。類簇內距離和Ein值越小，意味著所有類簇中的數據樣本越緊湊，聚類的緊密型越好。

另外，還需要計算各個類簇中心點相互間的距離作為類簇間距離，類簇間距離定義為Eout，類簇間距離Eout的計算公式為：

其中，k表示類的數目，即類簇數，Ci表示第i個類簇的聚類中心點，C表示各個類簇的聚類中心平均值，類簇間距離Eout的值越大，意味著類和類之間的相似度小。

綜合類簇內距離和Ein與類簇間距離Eout兩個值來評定聚類效果的優劣性，本文將類簇內距離和Ein與類簇間距離Eout的比值作為聚類效果的評價標準，當類簇內距離和Ein與類簇間距離Eout的比值越小時，表示此時的聚類效果越好。用EE表示聚類效果優劣程度的評價標準，則EE表示為：

由上式可以得出，EE值為先逐漸變小然后會慢慢變大，EE值越小，表示聚類的效果越好，當EE達到局部最小值時，聚類效果最佳，由此可以確定聚類數目K值。

2.2?算法描述

本文通過聚類數目K值的確定和優化初始聚類中心來改進傳統Kmeans算法。在確定聚類數目K值時，隨著EE=Ein/Eout的值不斷變小讓K++，當EE值達到局部最小值時來確定K值;優化初始聚類中心時，根據數據集樣本分布的特點，選擇出K個相距較遠的數據樣本作為初始聚類中心。本文基于優化初始聚類中心的Kmeans算法一方面解決了傳統Kmeans算法中聚類數目K值無法確定的問題，另一方面解決了傳統算法中隨機選取初始中心點而造成的局部最優問題。

本文基于優化初始聚類中心的Kmeans算法具體描述如下：

（1）初始化：K=1，運行傳統的Kmeans算法并計算此時的EE值;

（2）讓K++，再次運行傳統的Kmeans算法并記錄EE;

（3）隨著K的逐漸增大運行Kmeans算法，直到EE值出現局部最小值，保留此時的K值，由此確定聚類數目K值;

（4）選擇數據集中任意一個數據對象作為第一個聚類中心點;

（5）重復步驟（4），選取出K個初始的聚類中心點;

（6）計算數據集剩余樣本到離得最近聚類中心的距離，定義該距離為D（X）;

（7）為每個類重新選擇聚類中心點，此時選取概率與D（X）的大小成正比，即離原聚類中心越近的點越有可能被選取為新的聚類中心點;

（8）重復步驟（7）直到K個聚類中心點全部被選出來;

（9）再運行傳統的Kmeans聚類算法。

3?實驗結果與分析

本文實驗環境為：Intel?CPU，8GB內存，500G硬盤，Windows10操作系統和MATLAB應用軟件。

在UCI機器學習數據庫[7]的Iris等6個聚類算法常用的測試數據集上對本文基于優化初始聚類中心的改進Kmeans算法和傳統Kmeans算法進行實驗測試并比較。UCI數據集的描述見表1。

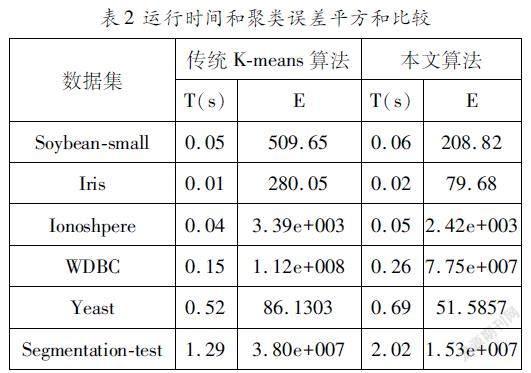
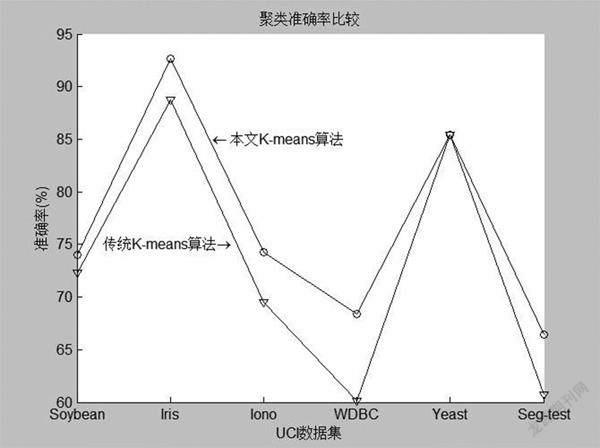
采用聚類誤差平方和、聚類時間和聚類準確率、Rand指數、Jaccard系數[89]，“Adjusted?Rand?index”參數[10]對聚類算法的運行結果進行比較分析。表2是本文基于優化初始聚類中心的Kmeans算法和傳統Kmeans算法的聚類誤差平方和與聚類時間比較的結果。圖1～圖4分別是兩種算法的Rand指數、Jaccard系數、“Adjusted?Rand?index”參數和聚類正確率的比較結果。

從表2可以看出，在各個數據集上，本文基于優化初始聚類中心的Kmeans算法的聚類誤差平方和都小于傳統Kmeans算法，有良好的聚類效果。聚類時間的比較顯示，本文算法的時間性能略差于傳統Kmeans算法，分析原因在于本文算法在確定K值和選取聚類中心點時會消耗一定的時間。

圖4顯示，在所有數據集上本文基于優化初始聚類中心的Kmeans算法的聚類正確率優于傳統Kmeans算法。因此，本文算法獲得良好的聚類效果，獲得較高的聚類準確率。

結語

本文在分析傳統Kmeans聚類算法不足的基礎上，提出一種基于優化初始聚類中心的Kmeans算法。該算法通過量化樣本間距離和聚類的緊密性來確定聚類數據K值，利用數據集樣本的分布特征選取相距較遠的初始聚類中心點，克服了傳統Kmeans算法對初始聚類中心敏感、聚類效果不理想的缺陷。在UCI機器學習數據庫數據集上的實驗表明：本文基于優化初始聚類中心的Kmeans算法有很好的聚類效果，準確率高，聚類性能優于傳統Kmeans算法。

參考文獻：

[1]孫吉貴，劉杰，趙連宇.聚類算法研究[J].軟件學報，2008，19（1）：4861.

[2]Han?J?W，Kamber?M.Data?Mining：Concepts?and?Techniques，2nd?ed.[M].Beijing：Chain?machine?Press，2000：383466.

[3]謝娟英，郭文娟，謝維信，等.基于樣本空間分布密度的初始聚類中心優化K均值算法[J].計算機應用研究，2012，29（3）：888892.

[4]韓凌波，王強，蔣正峰，等.一種改進的kmeans初始聚類中心選取算法[J].計算機工程與應用，2010，46（17）：150152.

[5]黃敏，何中市，邢欣來，等.一種新的kmeans聚類中心選取算法[J].計算機工程與應用，2011，47（35）：132134.

[6]熊忠陽，陳若田，張玉芳.一種有效的Kmeans聚類中心初始化方法[J].計算機應用研究，2011，28（11）：41884190.

[7]Frank?A，Asuncion?A.UCI?machine?learning?repository[EB/OL].Irvine，CA：University?of?California，School?of?Information?and?Computer?Science，2010.http：//archive.ics.uci.edu/ml.

[8]張惟皎，劉春煌，李芳玉.聚類質量的評價方法[J].計算機工程，2005，31（20）：1012.

[9]于劍，程乾生.模糊聚類方法中的最佳聚類數的搜索范圍[J].中國科學（E輯），2002，32（2）：274280.

[10]楊燕，靳蕃，Kamel?M.聚類有效性評價綜述[J].計算機應用研究，2008，41（06）：16311632.

基金項目：甘肅政法大學校級青年項目（GZF2019?XQNLW08），甘肅省青年科技基金項目（21JR7RA572），2019年甘肅省高校引進和使用優質在線開放課程項目

作者簡介：郭文娟（1986—?），女，甘肅武威人，講師，研究方向：智能信息處理。