球軸承變柔度1/2階亞諧共振的滯后特性及其分岔機理

朱宇杰， 張智勇,,， 陳毅恒， 芮筱亭， SATTEL Thomas， 陳予恕， 楊紹普

(1. 南京理工大學 理學院，南京 210094； 2. 南京理工大學 發射動力學研究所，南京 210094；3. 伊爾默瑙工業大學 機械工程學院，伊爾默瑙 98684； 4. 哈爾濱工業大學 航天學院，哈爾濱 150001；5. 石家莊鐵道大學 省部共建交通工程結構力學行為與系統安全國家重點實驗室，石家莊 050043)

制造業是工業經濟最重要的支柱，機械工業在制造業中的占比接近2/3，其中軸承產業直接或間接地影響著我國20萬億人民幣以上規模的經濟量[1]。滾動軸承由于其低阻尼、大過載和小體積等特點，是旋轉機械的主要支承件和傳動部件。軸承滾動體在自轉的同時隨保持架在滾道內繞轉軸公轉，不可避免地會引起軸承支承剛度時變特性，并誘發系統的變柔度(varying compliance，VC)參激振動[2-3]。一般而言，健康軸承對其支承系統振動特性的影響主要體現在彈性支承和VC時變激勵兩個方面[4-5]，在軸承-轉子系統動力學設計過程中應充分考慮滾動軸承的激振特性。

滾動軸承被視為本質非線性機械件[6]，包含滾動體與滾道之間的Hertzian接觸、軸承游隙以及VC參激等多種非線性因素，由此帶來的軸承-轉子系統的滯后突跳振動研究，歷來屬于軸承-轉子動力學領域的基本科學問題[7-9]。我國現役某型軍機航空發動機在高壓轉子前支承球軸承處就曾多次出現超過故障判據的異常突跳振動現象，導致該型軍機發動機多次提前返廠修理。Sunnersj?較早分析了考慮慣性力的線彈性圓柱滾子軸承模型，發現VC振動可以給系統帶來周期運動和不規則的非周期運動。Fukata等針對考慮Hertzian接觸和軸承徑向游隙非線性的經典兩自由度軸承模型，發現系統在一階VC共振頻率區間具有亞諧、準周期和類混沌運動行為。Mevel等[10-11]對該模型進行進一步的理論和試驗，探討了球軸承VC振動通向混沌的道路，發現系統在一階臨界轉速區間存在倍周期分岔失穩進入混沌運動的形式。Sankaravelu等[12]把打靶法與同倫延拓法相結合，發現滾動軸承VC振動幅頻響應曲線具有滯后跳躍行為。之后，Ghafari等[13-15]也分析了滾動軸承VC滯后突跳或其雙穩態現象。從Hertzian接觸共振角度出發，Zhang等[16-17]采用諧波平衡-頻時轉換(harmonic balance and alternating frequency/time domain，HB-AFT)方法，研究發現球軸承在VC參激接觸主共振區間具有軟滯后和交叉滯后共振行為。隨后，Jin等[18]對上述共振特性進行了試驗驗證。另外，Zhang等[19]指出球軸承主共振區間的倍周期分岔行為可由系統不同自由度方向上的VC參激1∶2內共振引起，并給出了一類有效的控制VC運動周期倍化的方法。上述研究主要針對滾動軸承VC主共振區間的響應特性展開。然而，根據非線性振動基本理論，參激系統往往具有豐富的主共振、內共振、超諧、亞諧和組合共振行為，因此相關工作有待深入展開。

學者們對不同類型非線性振動系統的亞諧共振及其失穩特性展開了廣泛研究，在種群系統[20]、湍流演化[21]、分子動力學[22]、微機電系統(micro-electro-mechanical system，MEMS)[23]、電動力學[24-25]、能量采集[26]等領域針對亞諧共振研究取得了系列成果。就軸承轉子系統而言，隨著旋轉機械向高速、重載和自動化方向發展，這對滾動軸承-轉子系統的穩定性、安全性提出了更高的要求，促進了研究者對轉子系統亞諧共振的深入研究。Ehrich[27]基于對系統有限差分方程數值積分，分析了考慮軸承游隙的轉子系統彎曲振動響應特性隨轉速的變化規律，發現在低阻尼和強非線性情形下系統可能發生高階亞諧振動行為。Yoshida等[28]研究了考慮重力和Hertzian非線性的非對稱球軸承-Jeffcott轉子系統在不平衡激勵下的響應特性，文中對于Hertzian接觸1.5次冪非線性支承力項采用包含線性項和三次非線性項恢復力的形式擬合替代，采用多性尺度法研究了系統的共振幅頻特性，并對其穩定性進行了分析。理論和試驗表明，系統在轉速約為水平和垂直方向上自然頻率的兩倍的情況下，在重載和非重載方向分別具有軟、硬滯后1/2階亞諧共振特性。另外，該文發現系統在兩個1/2階亞諧共振區間具有組合共振特性，但未作深入研究。Bai等[29]建立了考慮球軸承Hertzian接觸力、軸承游隙以及轉子彎曲振動在內的六自由度非線性轉子模型，利用軸心軌跡和幅頻響應曲線研究了系統在不平衡激勵下的亞諧共振特性，并且采用Floquet理論分析了系統響應的失穩特性，所得結果與試驗數據吻合。他們指出球軸承亞諧共振是由于系統的Hertzian接觸力和軸承游隙等非線性因素共同作用的結果。Hou等[30]研究了盤旋狀態下非線性剛度、阻尼、偏心距和操縱負荷對飛行器轉子系統共振特性的影響，發現偏心距和操縱負荷越大，觸發的亞諧共振越強。Wu等[31]針對包括多個裝配間隙的轉子-軸承-基座系統，采用Jones-Harris方法獲得了考慮預緊的角接觸高速球軸承的等效非線性支撐剛度，通過建立系統的集總參數模型分析了不平衡激勵和間隙對系統振動響應幅度的影響。發現系統具有亞諧滯后共振響應特性，且隨著裝配間隙的增加，系統的振動響應幅度和共振跳躍行為會更加突出，同時系統的共振位置向低頻移動。目前為止，如上所述國內外主要針對不平衡激勵下轉子系統的亞諧共振特性進行了研究，并未深入分析軸承-轉子系統VC參激下的亞諧共振行為。

HB-AFT方法利用AFT時域離散化技術，能夠快速得到非線性項的頻域信息，進而完成非線性系統的諧波平衡過程，實現對一般非線性系統穩態諧波響應的求解[32]。Kim等[33-34]為了分析多自由度、多頻激勵系統的準周期響應特性，發展了廣義HB-AFT方法。Zhang等將同倫延拓技術嵌入HB-AFT方法，結合Hsu求解Floquet單值矩陣的離散方法，能夠自動追蹤非線性系統周期響應及其分岔特性。最近，Chen等[35]利用系統整體傳遞矩陣階數與系統的自由度數無關的特點，給出了結合模型增量傳遞矩陣的諧波平衡方法，提升了諧波平衡法求解多自由度系統周期響應的效率。

本文針對球軸承VC參激亞諧共振研究甚少的現狀，將以HB-AFT方法和Floquet理論為主要分析手段，深入研究球軸承系統VC參激1/2階亞諧共振響應的觸發機制、滯后跳躍特性及其分岔失穩機理，并擬探究軸承徑向游隙、阻尼等系統主要參數對復雜亞諧共振行為的影響規律。

1 球軸承VC振動描述

本文采用經典的兩自由度深溝球軸承模型，如圖1所示。圖1中的模型包含滾動體與滾道之間的Hertzian接觸、軸承游隙以及VC參激等因素，已有研究表明，該球軸承-剛性Jeffcott轉子模型能夠較好地定性和定量反映系統徑向VC振動的響應特性，特別是在軸承徑向跳動分析中具有重要價值。本文所研究的JIS6306球軸承的具體規格參數，如表1所示。

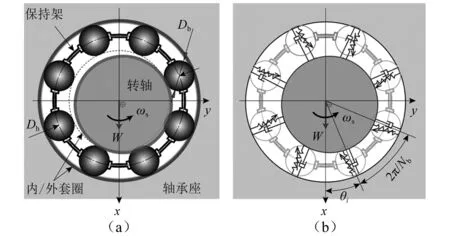
圖1 球軸承系統及其兩自由度彈簧模型Fig.1 The ball bearing system and its two-degree-of-freedom spring model

表1 JIS6306球軸承的規格參數Tab.1 Specifications of JIS6306 ball bearing

見圖1，第i個滾動體的瞬時角位置為

θi=2π(i-1)/Nb+Ωt

(1)

其中，滾動體通過角頻率(即保持架轉速)

Ω=ωs(1-Db/Dh)/2

(2)

則第i個滾動體與軸承套圈的接觸變形表示為

δi=xcosθi+ysinθi-δ0

(3)

式中：ωs為轉軸轉速； 2δ0為軸承的徑向游隙。

假設滾動體和滾道之間滿足Hertzian點接觸受力變形關系，則球軸承恢復力滿足

(4)

式中，G[·]為Heavisde函數。當δi≥0時，G[δi]=1，表示第i個滾動體與滾道接觸；當δi<0時，G[δi]=0，表示第i個滾動體與滾道接觸失去接觸。

根據球軸承恢復力式(4)，球軸承-剛性Jeffcott轉子系統VC運動微分方程可表示為

(5)

滾動軸承滾動體與滾道之間具有Hertzian接觸變形關系使系統可具有硬彈簧特性[36]，靜載Ws作用方向上球軸承系統的近似線性化靜態剛度可表示為

(6)

式中，δWs為Ws作用方向上的總體變形。

顯然，式(6)并不適用于球軸承系統運轉過程中動態剛度的估計。然而，滾動軸承動態剛度特性對于其支承系統的非線性響應特性具有顯著的影響。根據恢復力式(4)，可近似估計系統的徑向線性化動態剛度

(7)

則系統的動態共振頻率(嚴格來說非線性振動系統不存在固有頻率)表示為

(8)

則系統兩自由度方向上等效共振頻率ωx0，ωy0可由式(8)算術平均值來估計。

就球軸承VC參激振動而言，系統的VC參激頻率與滾珠個數相關，可表示為

ΩVC=NbΩ

(9)

一般而言，參激系統可能激起豐富的共振行為[37-39]。對于本文研究對象，系統可能觸發的VC參激主共振、亞諧和超諧共振的頻率條件為

ΩVC≈{nωxx,mωyy, 1/jωxx, 1/kωyy}

(10)

且當n(m)=1時，系統發生VC參激主共振；當n(m)=h時，系統可能在x(y)方向上激起1/h階亞諧共振；當j(k)=1/h時，系統可能在x(y)方向上激起h階超諧共振。另外，系統可能觸發VC參激組合共振的頻率條件包含

ΩVC≈nωxx±mωyy±u/jωxx±v/kωyy

(11)

式中，h，m，n，j，k，u和v均為整數(j，k非零)，且h≠1。

值得注意的是：由于系統非線性動態剛度的滯后特性，使系統可能具有多種共振響應共存的多穩態現象[40]。

2 研究方法

對于周期激勵非線性振動系統，把響應周期是系統激勵周期M倍的周期解稱為系統周期M解。因此，在1/M階亞諧共振區間，系統一定具有周期M解，即包含周期M運動。下面給出本文研究式(5)的VC周期M解求解及其穩定性分析過程。

2.1 HB-AFT方法求解VC周期M響應

為了提高求解精度和效率，首先對式(5)進行時間和位移尺度的無量綱化，令τ=NbΩt/M，X=[X,Y]T=[x/δ0，y/δ0]T，則式(5)可以表示為

X″(τ)=F[X(τ),X′(τ),λ]

(12)

因本文求解系統的幅頻響應曲線，令其中控制參數λ=Ω。此時，原式(5)的VC參激周期M響應，對于無量綱式(12)而言，其無量綱響應周期TVC為2π，則可把式(12)的位移X(τ)和非線性力F(·)表示為

(13)

把式(13)代入式(12)，諧波平衡可得代數關系式

g(P,Q,λ)=0

(14)

式中，X(τ)和F(·)的諧波系數表示為

(15)

式(14)由2K+1個代數方程組成，包含P，Q共計4K+2個未知諧波系數，因此不能直接求解位移響應X(τ)(即求解P)，需要首先把Q由P來表示，此過程由下述AFT技術實現。

采用反有限Fourier變換得到X(τ)的時域離散信息

(16)

由式(12)可得非線性力的時域離散信息

F(n)=F[X(n),X′(n),λ]

(17)

那么，通過有限Fourier變換可得

(18)

上述AFT過程中：Pk=ak+ibk；Qk=ck+idk；N為一個時域周期內的采樣點數，且n=0, …,N-1；當n=0時，φ=1，否則φ=2。

式(18)得到了由P表示Q的關系式。設P為未知變量，接下來可通過求解非線性代數方程式(14)求得系統的X(τ)諧波解。為了避免在轉向點(即折疊分岔點)迭代求解失效，并實現隨控制變量λ的系統周期M解分枝的自動追蹤求解，引入弧長延拓過程，把式(14)轉換為

(19)

式中，s為曲線[P(s),λ(s)]的弧長變量，采用經典的預估校正法即可實現式(19)的求解[41]，這里不再累述。

2.2 VC周期M響應Floquet穩定性分析

2.1節基于HB-AFT方法可求得系統VC周期M解U*(τ)，下面基于Floquet穩定性理論[42]給出該解穩定性分析的基本過程。

設U=[X,X′,Y,Y′]T=[X1,X2,X3,X4]T，根據式(5)，可把無量綱式(12)變換為

(20)

式中，ΩM=NbΩ/M。

由式(20)，用ΔU擾動VC周期M解U*(τ)，即

[U*(τ)+ΔU]′=H[τ,U*(τ)+ΔU]

(21)

進一步可得關于擾動項的下述線性近似關系

ΔU′=?H[τ,U*(τ)]/?U*(τ)·ΔU

(22)

則U*(τ)的局部線性穩定性可由式(22)中ΔU的穩定性來判斷。由于U*(τ)為式(20)的周期M解，則?H[τ,U*(τ)]/?U*(τ)同樣是周期為2π的周期變系數矩陣。因此，可以采用Floquet理論對式(22)來判定系統VC周期M解的穩定特性。

借助HB-AFT方法求得的系統VC周期M解U*(τ)，采用Hsu方法可以方便計算式(20)的Floquet單值矩陣，進而判斷系統的Floquet乘子(即單值矩陣的特征值，記為λm)。根據λm通過復平面單位圓的方式可知系統VC周期M解的三類基本的失穩形式：

(1) 當Floquet主乘子由+1軸越出單位圓時，系統周期響應可能發生折疊分岔、跨臨界分岔和對稱破缺分岔，其中折疊分岔僅在系統周期軌線轉向點位置出現；

(2) 當Floquet主乘子由-1軸穿出單位圓時，系統周期響應發生倍周期分岔；

(3) 當Floquet共軛乘子離開單位圓時，周期響應發生二次Hopf分岔。

3 結果與討論

3.1 VC參激1/2階亞諧共振的觸發機制及其分岔特性(δ0=1.2 μm，c=200 N·s/m)

在軸承徑向間隙δ0=1.2 μm時，以保持架轉速Ω為控制參數，如圖2所示，采用嵌入弧長延拓的HB-AFT方法可追蹤系統的VC周期1和周期2解分枝。利用式(8)預測系統x，y兩自由度方向的等效主共振頻率ωx0，ωy0分別為1 910.1 rad/s，1 331.4 rad/s，則由式(9)可知，系統兩自由度的VC參激主共振頻率分別為ωx0/Nb=238.761 4 rad/s和ωy0/Nb=166.424 4 rad/s。因此，圖2區域a-a和b-b分別是系統x，y方向的VC主共振區間。此時，系統在兩個主共振區間分別表現出軟的滯后共振和交叉共振行為，這與已有的理論和試驗結果一致。同時，系統在兩倍的參激主共振頻率477.522 8 rad/s和332.848 8 rad/s附近再次觸發共振響應，由此可預測c-c和d-d區間的共振峰分別為系統在x，y方向的1/2階VC亞諧共振區間。

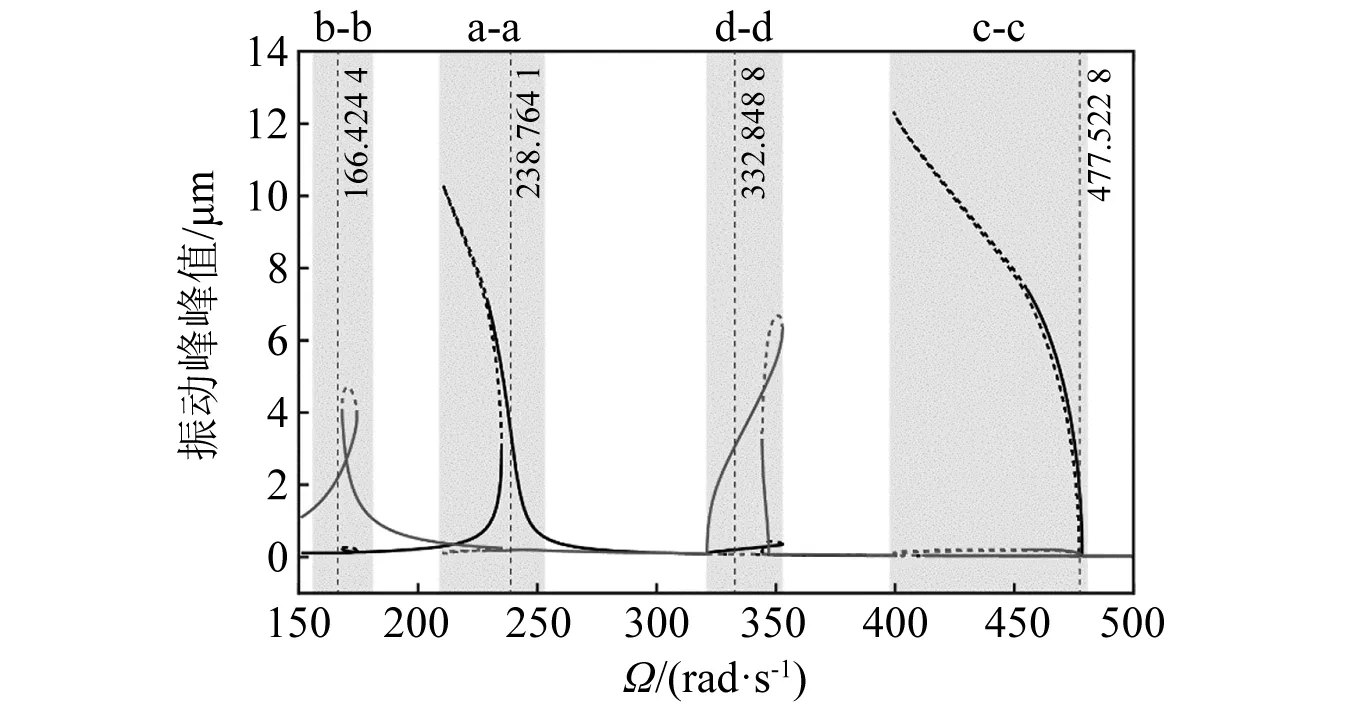
圖2 x(黑線)、y(灰線)方向穩定(實線)和不穩定(虛線)的VC周期解頻響曲線Fig.2 Stable (solid) and unstable (dashed) VC periodic frequency-response curves in x (black line) and y (gray line) direction

就亞諧共振分岔特性而言，系統在y方向1/2階亞諧共振區間依然表現出交叉共振滯后特性，如圖3所示。由Floquet穩定性分析可知：穩定的VC周期1解分枝的主Floquet乘子在點A1，如表2所示，點A2通過-1軸離開單位圓，由超臨界倍周期分岔失穩激起VC周期2解分枝，進而觸發y方向1/2階亞諧共振；穩定的VC周期2解分枝的主Floquet乘子在點A3，如表3所示，點A4穿過+1軸離開單位圓，導致系統由折疊分岔失穩發生滯后跳躍行為。例如，隨著控制參數Ω的增加，穩定的周期2解分枝在折疊分岔點A4突跳至穩定的周期1解分枝點A5的位置。隨著轉速Ω的增大，如圖4和圖5所示，系統VC周期1解分枝分別在點B1和點B2由亞臨界和超臨界倍周期分岔觸發周期2解分枝，進而激起x方向上的1/2階亞諧共振響應，此時的VC周期2運動幅頻響應曲線向左偏，表現出軟的滯后共振特性，這與x方向主共振區間的滯后特性是一致的。另外，在x方向上1/2階亞諧共振區間，穩定的周期2解分枝在點B3由超臨界周期倍化失穩產生周期4解分枝，之后周期4解分枝同樣由超臨界周期倍化在點B4觸發周期8解分枝，而周期8解分枝隨著Ω的減小在點B5由折疊分岔發生了滯后跳躍行為。總之，1/2階亞諧共振響應是由倍周期分岔失穩激起的，且與不同自由度方向上的主共振響應的滯后特性相同。上述結果與采用極值法[43]繪制的數值分岔圖是吻合的，如圖6所示。

圖3 y方向1/2階亞諧共振區間y(τ)的頻響曲線Fig.3 Frequency-response curves of y(τ) in y direction 1/2 order subharmonic resonance

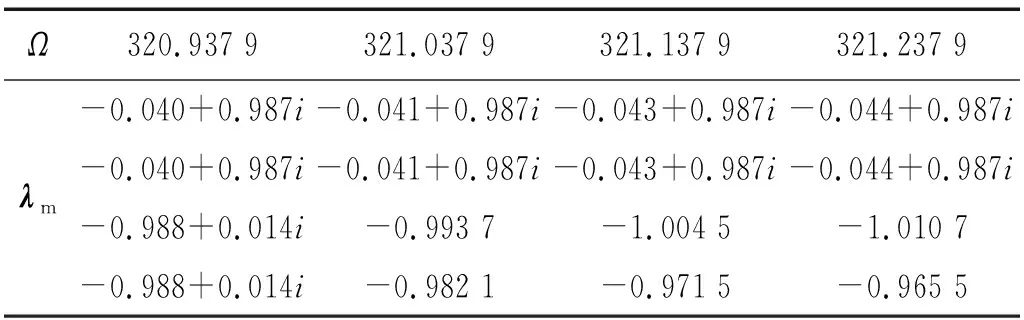
表2 周期1運動分支在點A1附近的 Floquet 乘子λmTab.2 Period-1 motion Floquet multipliers λm around A1

表3 周期2運動分支在點A3附近的 Floquet 乘子λmTab.3 Period-2 motion Floquet multipliers λm around A3

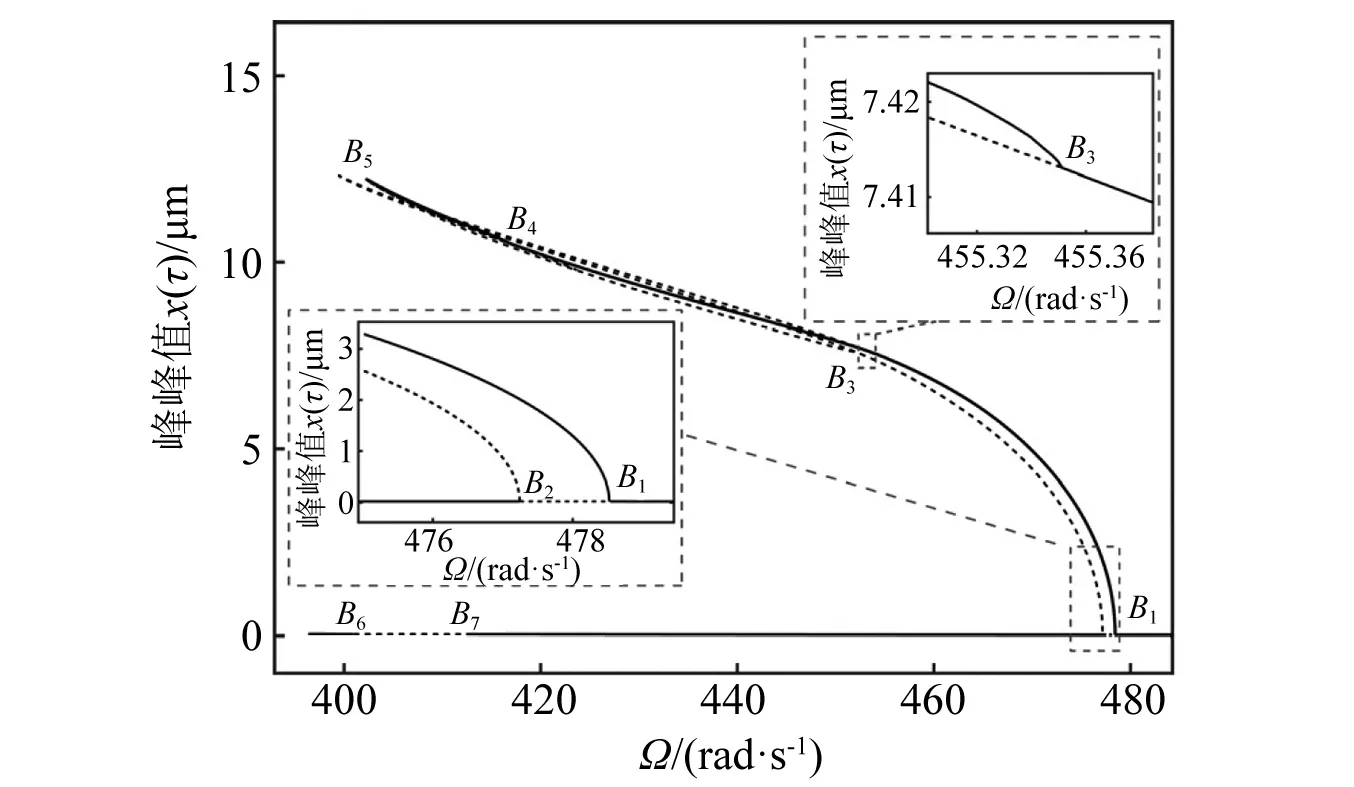
圖4 x方向1/2階亞諧共振區間x(τ)的頻響曲線Fig.4 Frequency-response curves of x(τ) in x direction 1/2 order subharmonic resonance

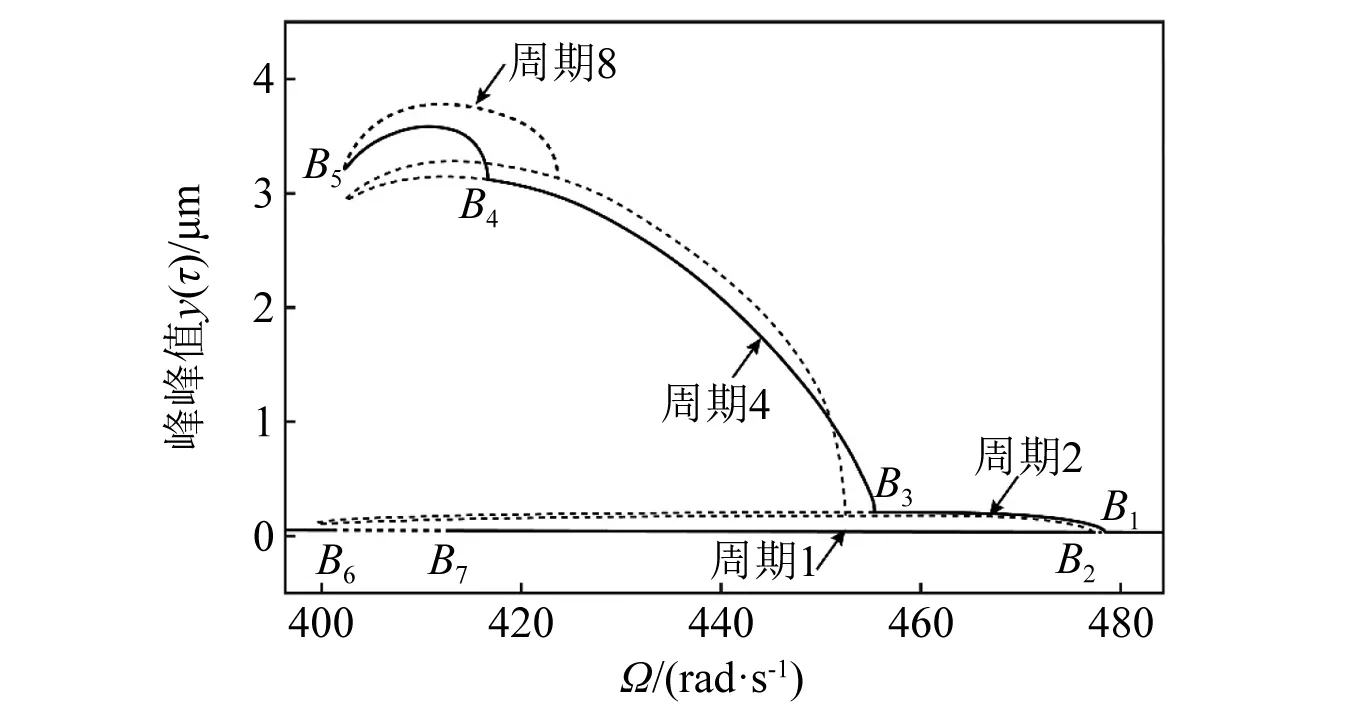
圖5 x方向1/2階亞諧共振區間y(τ)的頻響曲線Fig.5 Frequency-response curves of y(τ) in x direction 1/2 order subharmonic resonance

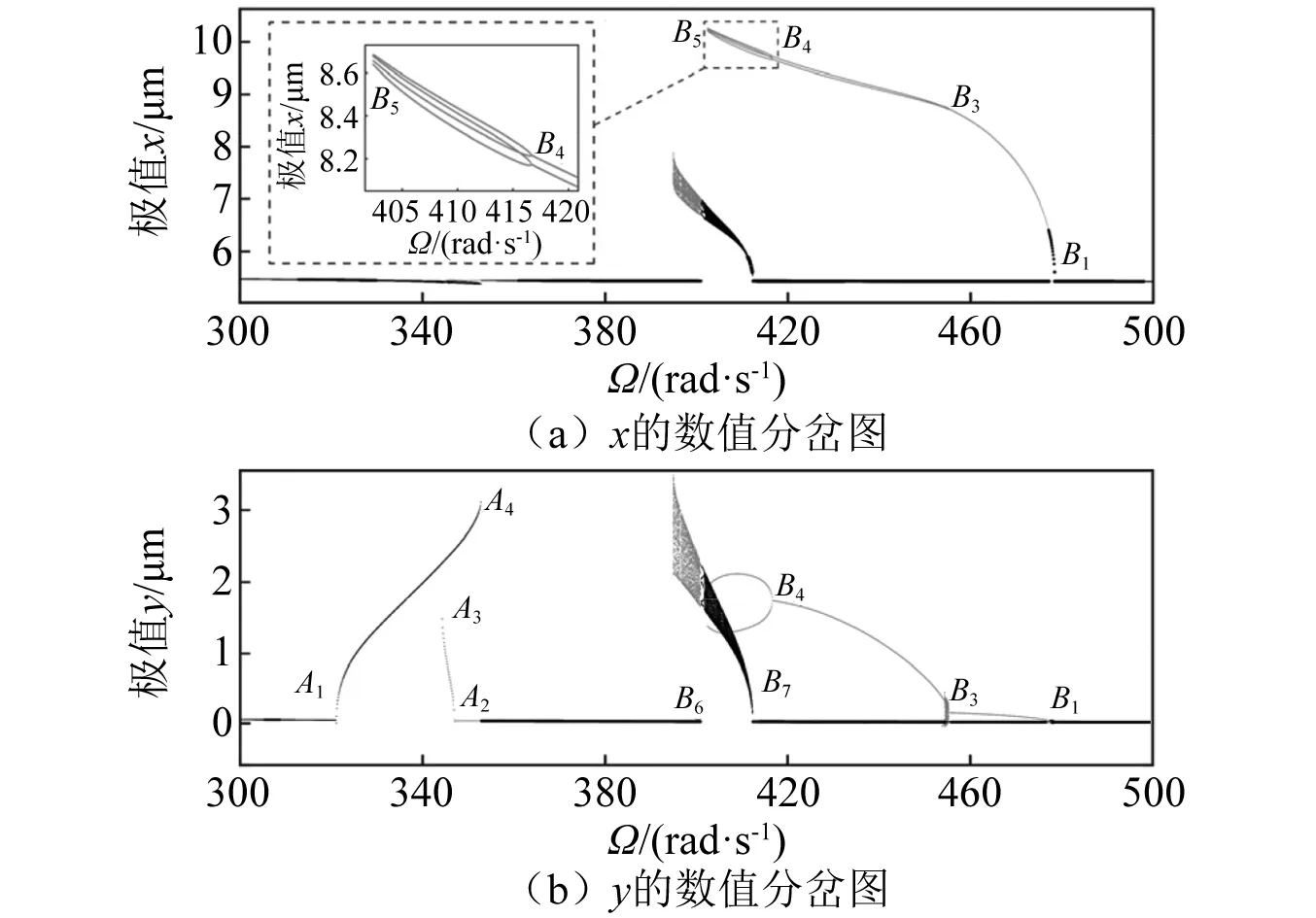
圖6 當δ0= 1.2 μm時，響應的數值分岔圖，其中黑點、灰點分別為Ω向上、向下掃頻的數值積分結果Fig.6 For δ0 =1.2 μm, numerical bifurcation diagrams, Ω sweeping up (black dots) and down (gray dots)

就響應特性而言，在y方向1/2階亞諧共振區間，如圖7所示，當Ω=340 rad/s時，系統時間歷程具有顯著的VC周期2運動特性，y(τ)相對于x(τ)表現出更大的1/2亞諧成分，此時兩自由度方向并未發生強烈的耦合振動(見圖2d-d區間)。在x方向1/2階亞諧共振區間，穩定的B1-B3周期2解分枝在兩自由度方向未發生強烈的耦合振動，故只有x(τ)表現出顯著的VC周期2運動特性(見圖4和圖5)。顯著不同的是：系統兩自由度方向在B3-B4周期4和B4-B5周期8解分枝上發生了強烈的耦合共振，此時y方向振動幅度顯著增加。對于B3-B4分枝，如圖8所示，當Ω=440 rad/s時，系統VC響應在x方向依然表現出周期2運動行為，此時卻在y方向激起強烈的VC周期4運動特性，展現出如Zhang等研究所示的1∶2耦合VC參激內共振響應特征。另外，對于穩定的VC周期8運動B4-B5分枝而言，如圖9所示，當Ω=410 rad/s時，系統VC運動在x方向依然表現出周期2響應行為，但在y方向表現出了顯著的VC周期8運動特性，此時系統發生了較為強烈的1∶4耦合參激內共振行為。

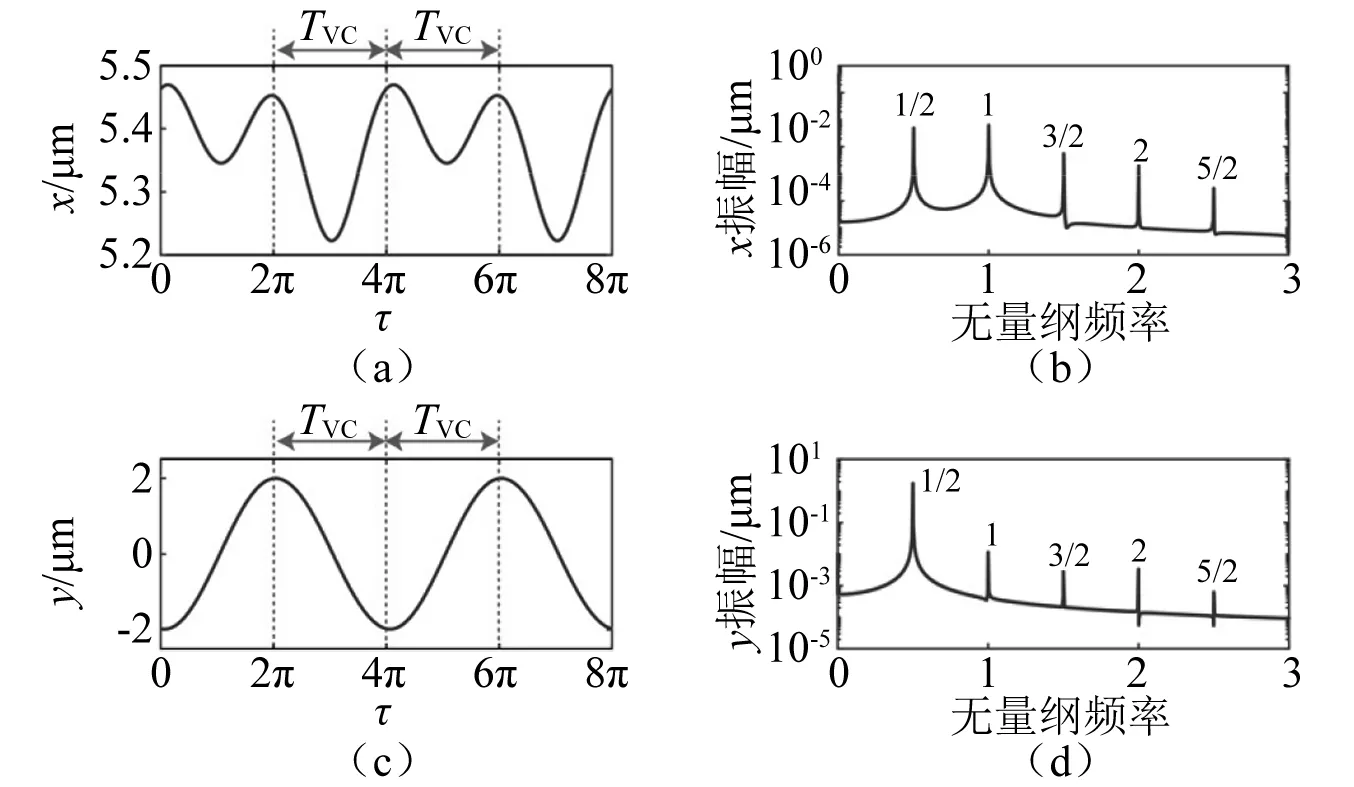
圖7 當Ω=340 rad/s時，x(τ)和y(τ)的時間歷程和頻譜圖Fig.7 For Ω=340 rad/s, time series and frequency spectrum of x(τ) and y(τ), respectively

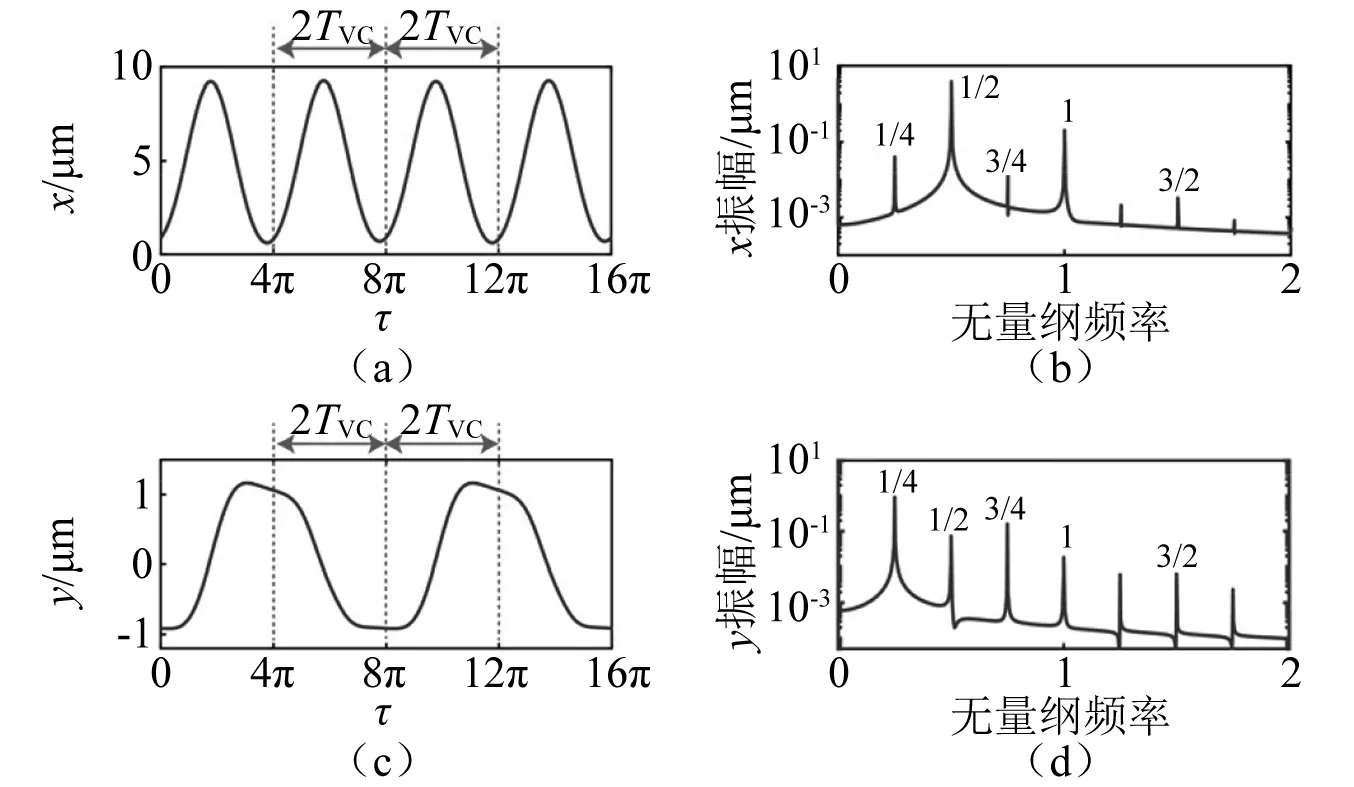
圖8 當B3-B4解分枝Ω=440 rad/s時，響應的時間歷程和頻譜圖Fig.8 For Ω=440 rad/s, time series and frequency spectra on B3-B4 solution branch

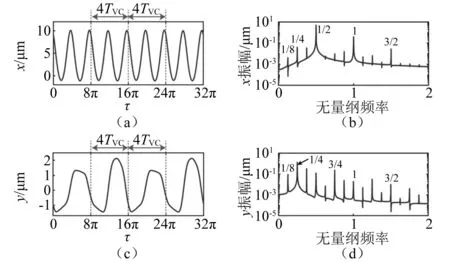
圖9 當B4-B5解分枝Ω=410 rad/s時，響應的時間歷程和頻譜圖Fig.9 For Ω=410 rad/s, time series and frequency spectra on B4-B5 solution branch

就共振類型而言，除了上述1/2階VC參激亞諧共振響應，系統在兩自由度方向上發生耦合，還觸發了顯著的VC參激組合共振行為。穩定的VC周期1解分枝(系統出現共軛Floquet乘子穿出了單位圓情形，如表4所示)在點B6和點B7由亞臨界和超臨界二次Hopf分岔失穩，因此在點B7激起穩定的VC準周期運動分枝(見圖5和圖6)。例如，在失穩的B6-B7周期1解分枝Ω=410 rad/s位置上，如圖10所示，因對應的VC準周期運動包含不可約頻率成分，響應軌跡的Poincare映射為封閉點集。此時，無量綱頻率成分p≈0.586，q≈0.414，因無量綱VC激勵周期為2π(見2.1節)，顯然p+q=1為系統的VC激勵頻率。而在原時間尺度下p，q對應的頻率值分別為Nb·Ω·p≈1 922.08 rad/s，Nb·Ω·q≈1 357.92 rad/s，接近前文所述系統兩自由度方向等效主共振頻率ωx0=1 910.1 rad/s，ωy0=1 331.4 rad/s。因此，可以推斷wx+ωy=ΩVC型組合共振是系統發生VC準周期運動分枝的內在機理，這屬于參激組合共振的一類基本特征[44-45]。

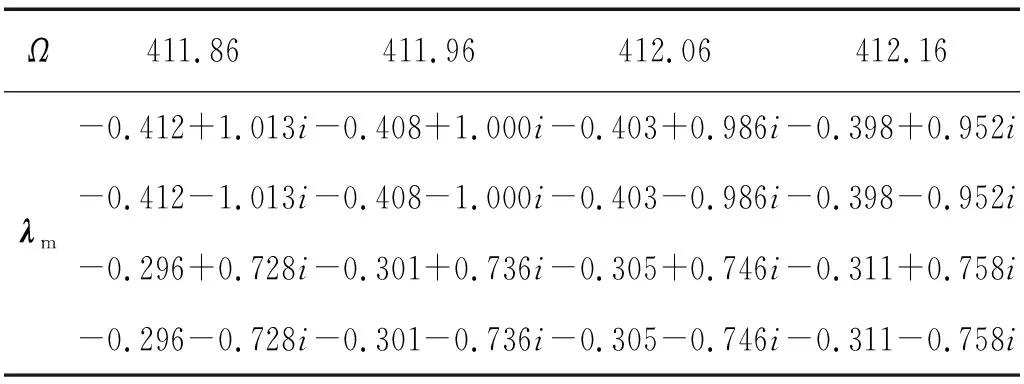
表4 周期1運動分支在點B7附近的Floquet乘子λmTab.4 Period-1 motion Floquet multipliers λm around B7

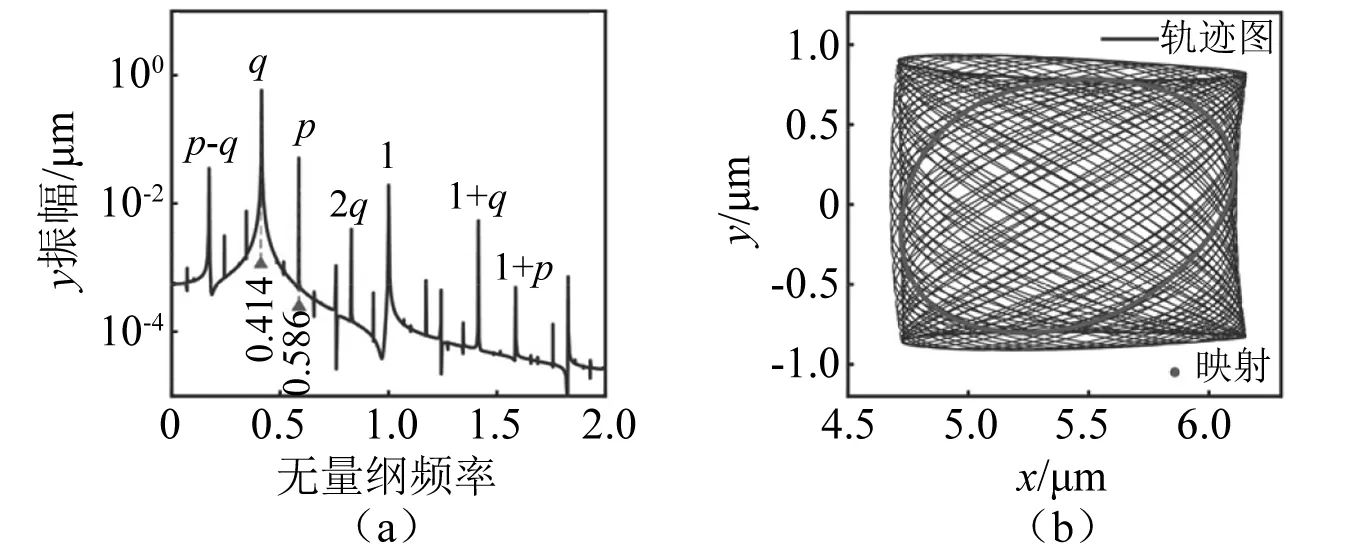
圖10 當B6-B7解分枝Ω=410 rad/s時，響應的頻譜和軌跡圖Fig.10 For Ω=410 rad/s, frequency spectra and orbit on B6-B7 solution branch

3.2 徑向游隙對VC參激1/2階亞諧共振的影響

游隙作為軸承的基本參數，對于滾動軸承的壽命、安裝和熱脹容量等具有重要的影響。由于其對軸承剛度能夠產生調節作用，下面將探討軸承徑向游隙δ0對系統亞諧共振行為的影響。當δ0=10 μm時，如圖11和圖12所示，由于系統y方向主共振位置e-e與x方向兩倍超諧共振位置f-f接近，因此，可能激起的y方向1/2階亞諧共振的頻率區間會與x方向主共振位置疊加，這導致x方向主共振位置穩定的周期1解在點C1和點C2由亞臨界倍周期分岔衍生出大范圍的周期2解分枝；另一方面，系統在x方向主共振區間附近還激起了兩個VC周期2封閉解分枝，其在y方向的振動峰值大于x方向的振動峰，即展現出y方向1/2階亞諧共振的響應特性。此時，系統x方向在點C3和點C4由倍周期分岔激起的具有軟滯后特性的1/2階亞諧共振區間變大，隨著控制參數Ω的減小，穩的1/2亞諧共振響應在點C5由亞臨界倍周期分岔失穩跳躍至封閉的VC周期4共振分枝C8-C9。周期4共振分枝C8-C9在y方向的共振峰幅度顯著，再根據其觸發位置可以認為是y方向1/4階亞諧共振響應的體現，上述分析結果與數值分岔圖13吻合。

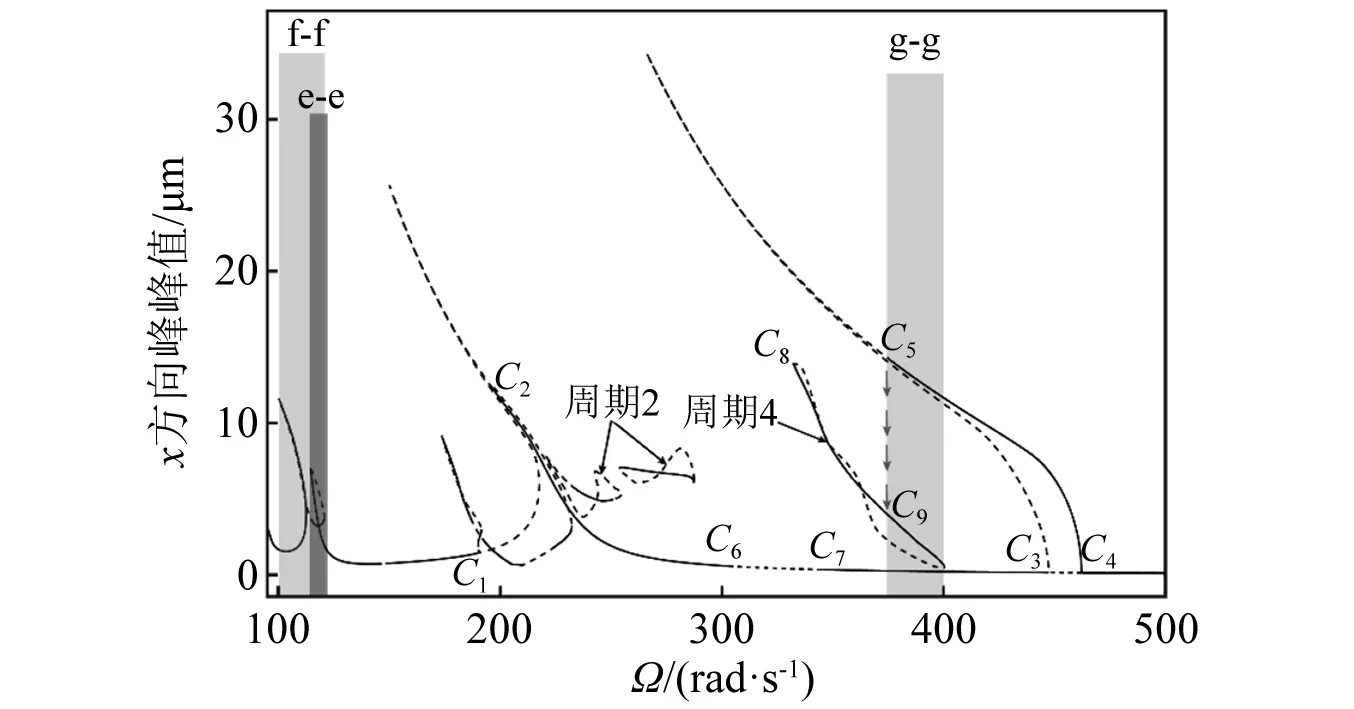
圖11 當δ0=10 μm，c=200 N·s/m時，x(τ)頻響曲線Fig.11 For δ0=10 μm and c=200 N·s/m, frequency-response curves of x(τ)

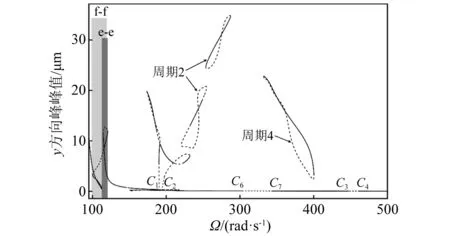
圖12 當δ0=10 μm，c=200 N·s/m時，y(τ)頻響曲線Fig.12 For δ0=10 μm and c=200 N·s/m, frequency-response curves of y(τ)

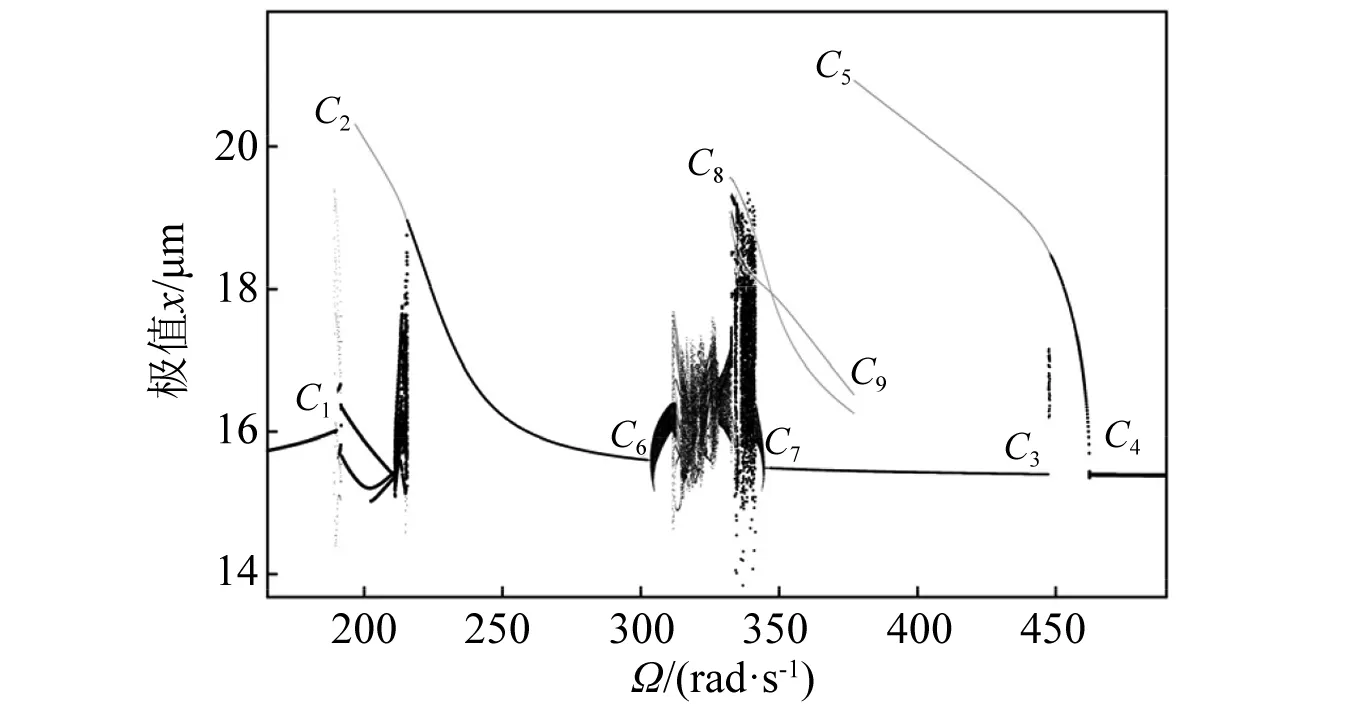
圖13 當δ0=10 μm，c=200 N·s/m時，x的數值分岔圖，其中黑點、灰點分別為Ω向上、向下掃頻的數值積分結果Fig.13 For δ0=10 μm, c=200 N·s/m, numerical bifurcation diagramsof x, Ω sweeping up (black dots) and down (gray dots)

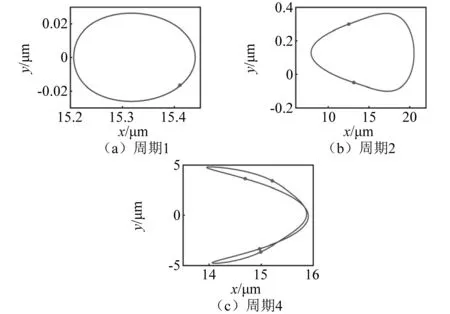
圖14 當δ0=10 μm，c=200 N·s/m，Ω=390 rad/s時，周期1、周期2和周期4多解共存響應特性Fig.14 For δ0=10 μm, c=200 N·s/m, Ω=390 rad/s, coexistence of period-1 motion, period-2 motion and period-4 motion

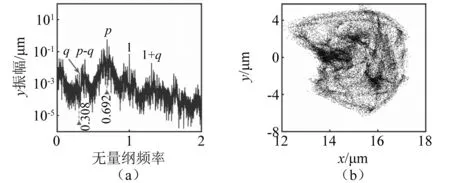
圖15 當δ0=10 μm，c=200 N·s/m，Ω=326 rad/s時，響應的頻譜和軌跡Poincare映射圖Fig.15 For δ0=10 μm, c=200 N·s/m, Ω=326 rad/s, frequency spectra and Poincare mapping of orbit of response

就參數影響規律而言，如圖16所示，對于x方向VC參激1/2階亞諧共振，隨著阻尼的增大亞諧共振失穩區間有減小的趨勢。相比而言，軸承徑向游隙對此類型亞諧共振觸發位置具有顯著的調控作用，如圖17所示，隨著軸承間隙逐漸減小(δ0取20.0 μm，10.0 μm和1.2 μm)，系統x方向1/2階亞諧共振失穩區間向高頻移動，且VC周期1運動上觸發亞諧共振的亞臨界和超臨界倍周期分岔點之間逐漸靠近。因此，可推測當軸承徑向游隙δ0減小到一定閾值時，x方向1/2階亞諧共振可得到抑制。當δ0=1.0 μm時，x方向1/2階亞諧共振并未觸發，如圖18所示，這與數值分岔圖19的結果吻合。此時，系統在分岔點D3和D4之間由亞臨界和超臨界二次Hopf分岔失穩同樣激起了ωx+ωy=ΩVC型組合共振響應。整體而言，對比圖2、圖11和圖18可以發現，隨著軸承間隙的變小，系統的復雜共振響應行為能夠得到很好的抑制。

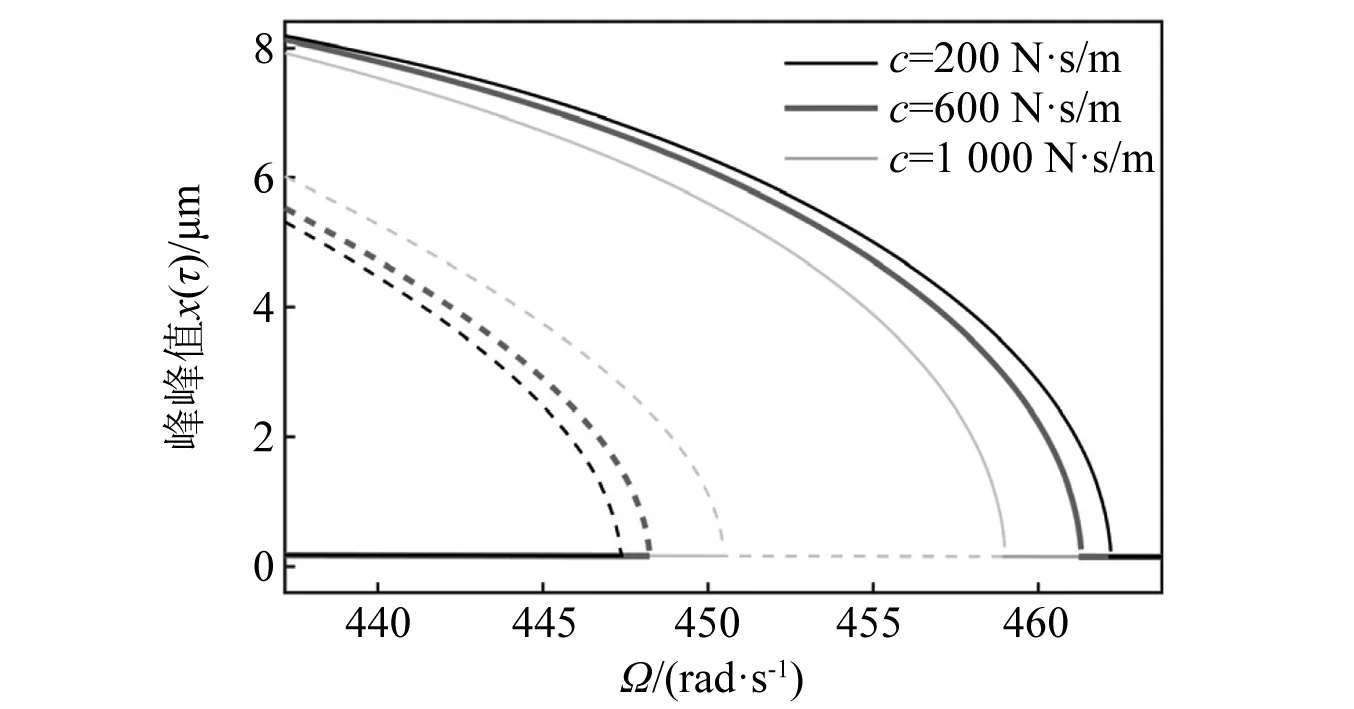
圖16 當δ0=10 μm時，阻尼c對1/2階亞諧共振x(τ)頻響的影響Fig.16 For δ0=10 μm, influence of damping c on x(τ) frequency-response curves of 1/2 order subharmonic resonance

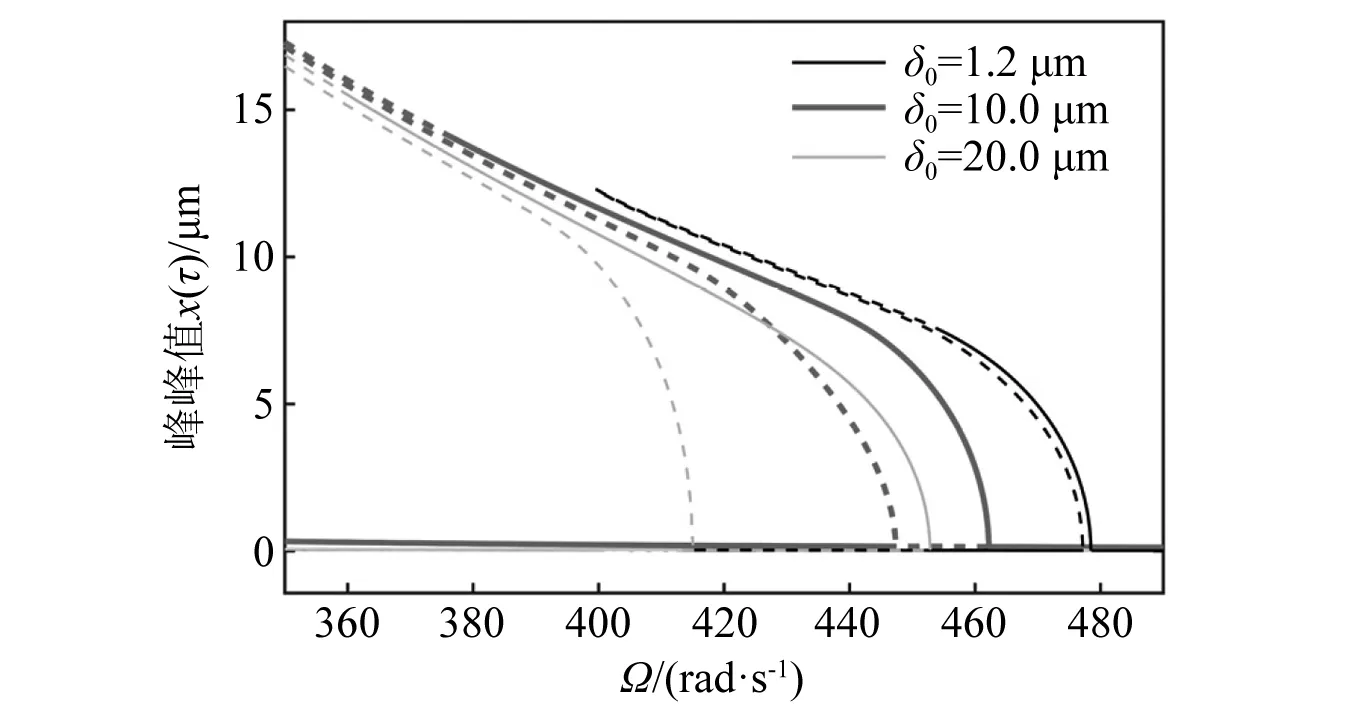
圖17 當c=200 N·s/m時，徑向游隙δ0對1/2階亞諧共振x(τ)頻響的影響Fig.17 For c=200 N·s/m, influence of radial clearance δ0 on x(τ) frequency-response curves of 1/2 order subharmonic resonance

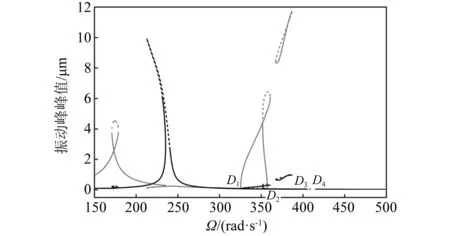
圖18 當δ0=1.0 μm，c=200 N·s/m時，x(黑線)、y(灰線)方向VC周期解頻響值曲線Fig.18 For δ0=1.0 μm, c=200 N·s/m, VC periodic frequency-response curves in x (black line) and y (gray line) direction

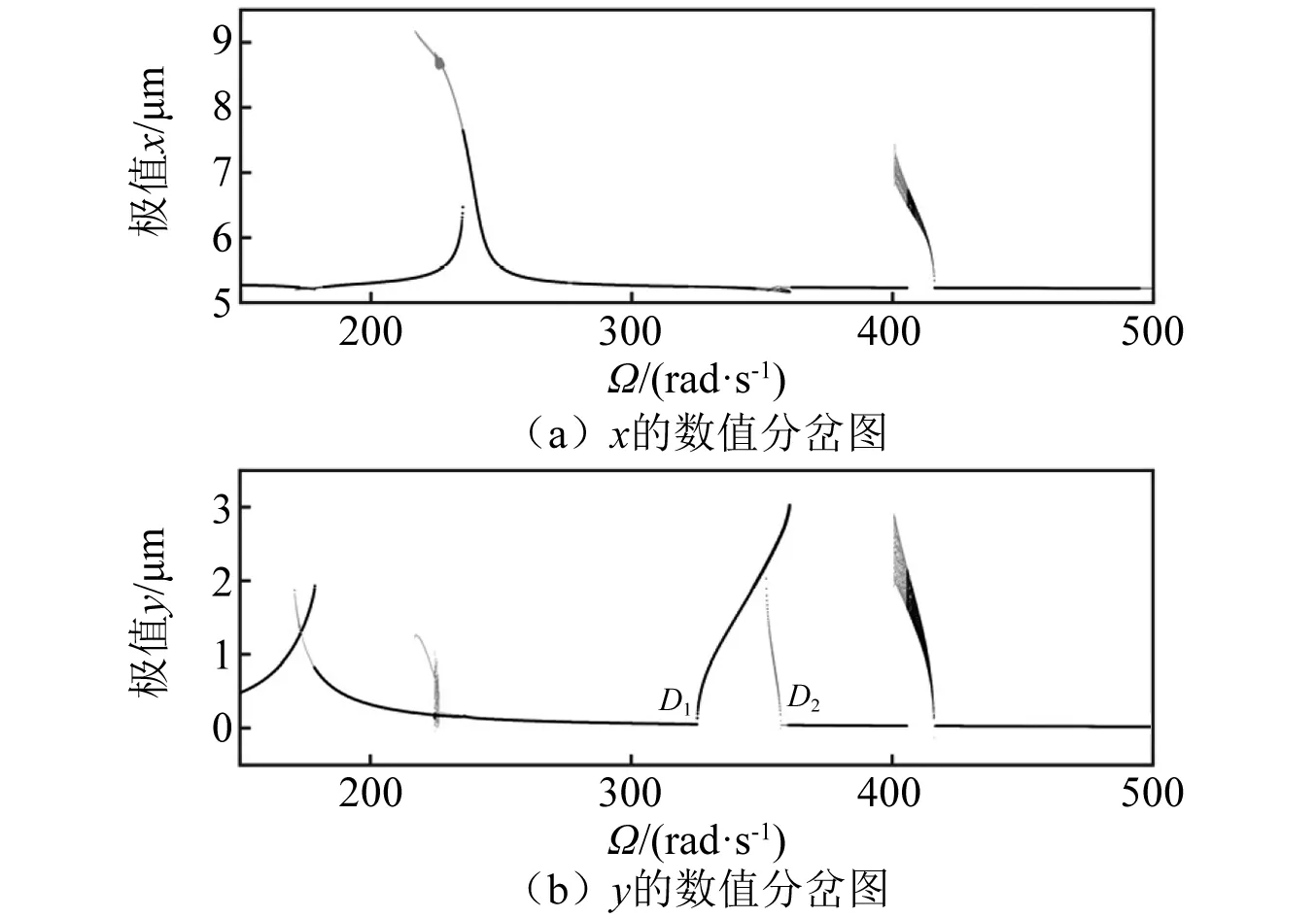
圖19 當δ0=1.0 μm，c=200 N·s/m時，響應的數值分岔圖，其中黑點、灰點分別為Ω向上、向下掃頻的數值積分結果Fig.19 For δ0=1.0 μm, c=200 N·s/m, numerical bifurcation diagrams, Ω sweeping up (black dots) and down (gray dots)

4 結 論

本文針對包括Hertzian接觸、軸承徑向游隙和VC參激非線性的球軸承模型，采用HB-AFT方法結合Floquet穩定性理論，研究了球軸承VC參激1/2階亞諧共振的觸發機制及其滯后響應特性。發現在VC參數激勵下，系統可在兩自由度方向上由亞臨界、超臨界倍周期分岔失穩激起1/2階亞諧共振行為。指出不同自由度方向上觸發的1/2階亞諧共振響應的軟、硬滯后類型與其對應的主共振滯后類型一致。研究表明，由于共振響應的滯后性，系統可能存在不同共振類型共存的響應區間，使系統VC振動可能具有豐富的滯后突跳、多解共存乃至耦合內共振行為，這會對軸承的壽命乃至其支承轉子系統運行的穩定性和安全性帶來潛在的影響。分析指出隨著軸承徑向游隙的減小，系統1/2階亞諧共振失穩區間向高頻移動且逐漸變小。因此，合理地選取軸承游隙能夠有效地調節亞諧共振的觸發位置和共振幅度。整體而言，隨著徑向游隙的變小，系統的復雜共振響應行為能夠得到很好的抑制。此外，研究發現VC參激還可由二次Hopf分岔失穩觸發系統的組合共振行為，由于不同自由度方向上的耦合作用，系統的組合共振響應具有顯著的準周期乃至混沌振動現象。

總之，對于滾動軸承這類型時變剛度參激系統，在其動力學設計過程中應充分考慮系統可能觸發的超諧、亞諧、內共振以及組合共振行為。本文對于滾動軸承復雜非線性振動響應行為的演化機制研究具有一定的參考意義。