高速鐵路三維輪軌瞬態滾動接觸-沖擊模型參數研究

王攀杰,劉建利,李 博,,安博洋

(1.西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031； 2.西南交通大學土木工程學院,成都 610031； 3.西安市軌道交通集團有限公司,西安 710000)

車輪在鋼軌上的滾動接觸是解決許多輪軌相關問題的關鍵，如磨損、塑性變形、滾動接觸疲勞(RCF)、車輛動力學和車輛-軌道相互作用。然而，目前缺乏精確測量滾動接觸問題(如接觸應力和應變狀態)的實驗方法，特別是在動態條件下[1]。因此，重點應放在分析和基于計算機的數值模擬方法上。

輪軌接觸研究始于19世紀，HERTZ[2]是最早用半空間假設提供彈性體之間無摩擦法向接觸解析解的研究者之一；MINDLIN[3]發展了赫茲接觸理論，推導出豎向或水平向荷載作用在半無限彈性體內部時體內任一點的應力與應變的數學解，從而來處理在摩擦極限內切向力引起的接觸體位移；CARTER[4]對輪軌摩擦滾動接觸進行了研究，利用二維分析模型計算了滾動方向上的黏著蠕滑現象；VERMEULEN和JOHNSON[5]通過假設一個橢圓的黏著面積，將CARTER的二維理論擴展到了具有純蠕變和無旋轉的三維理論；KALKER[6]用級數方法討論了具有橢圓形接觸區的三維滾動接觸問題，先后提出的線性理論、精確理論和簡化理論，是目前最廣為接受的計算方法，其相應的數值程序FASTSIM和CONTACT至今廣泛應用于車輛動力學和滾動接觸力學的求解。

近年來，隨著鐵路網運行速度、軸重和交通密度的不斷提高，輪軌滾動接觸的研究越來越受到重視，但經典的接觸力學理論由于本身存在的假設與局限性，已經難以滿足鐵路發展的需要。隨著計算機性能的發展，利用顯式時間積分方法進行瞬態有限元模擬，不僅可以考慮真實接觸幾何，也可考慮材料的非線性行為，使得有限元法更適合解決接觸條件和材料特性復雜度高的輪軌滾動問題。

許多學者利用有限元法解決了輪軌滾動接觸的一系列問題，諸如LI等[7-8]用顯式有限元方法解決了車輛-軌道交互系統中的輪軌滾動接觸問題；趙鑫團隊[9-11]利用此方法對高速輪軌瞬態滾動接觸行為進行了一系列研究；YANG等[12-14]通過顯式有限元分析，系統地探討了動態摩擦滾動接觸建模的核心算法；西南交通大學安博洋[15-16]、劉超[17]及寇峻瑜[18]分別研究了高速車輪擦傷引起的瞬態響應、車輛曲線通過時輪軌瞬態滾動接觸行為和高速車輪多邊形的動態響應，以上研究均取得了令人滿意的成果。上述研究在進行輪軌瞬態動力學模型計算過程中，所采用的大多為半輪對有限元模型，均沒有對不同模型參數所帶來的影響加以探究。顯式有限元方法的計算結果與模型的網格劃分、單元尺寸以及模型結構都有著密不可分的聯系，因此探究不同模型參數對瞬態計算的求解影響，并引入軌面不平順激勵，明確全輪對模型的適用范圍，從而為高速輪軌滾動接觸問題的精細化建模提供參考。

1 三維輪軌瞬態滾動接觸有限元模型

模擬我國某高速線路的車輛-軌道系統，研究不同模型參數條件下的瞬態計算模型在直線軌道上的輪軌滾動接觸行為。所建立的模型將真實的車輪和鋼軌幾何考慮在內，車輪踏面為LMa型，輪徑860 mm，鋼軌廓形為CHN60，模型結構如圖1所示。研究著重于高頻振動，因此，模型中輪軌、軌道板均用線彈性材料模型，以便考慮車軸、車輪和軌道的彈性變形。為便于表述，建立圖1所示的笛卡爾坐標系Oxyz，原點位于輪對初始位置A處軌道表面中心處，z軸和y軸分別沿縱向即滾動方向和垂向。車輛一系懸掛以上的所有部件被簡化為剛體或質點MC并通過一系懸掛(KS、CS)與車輪相連。

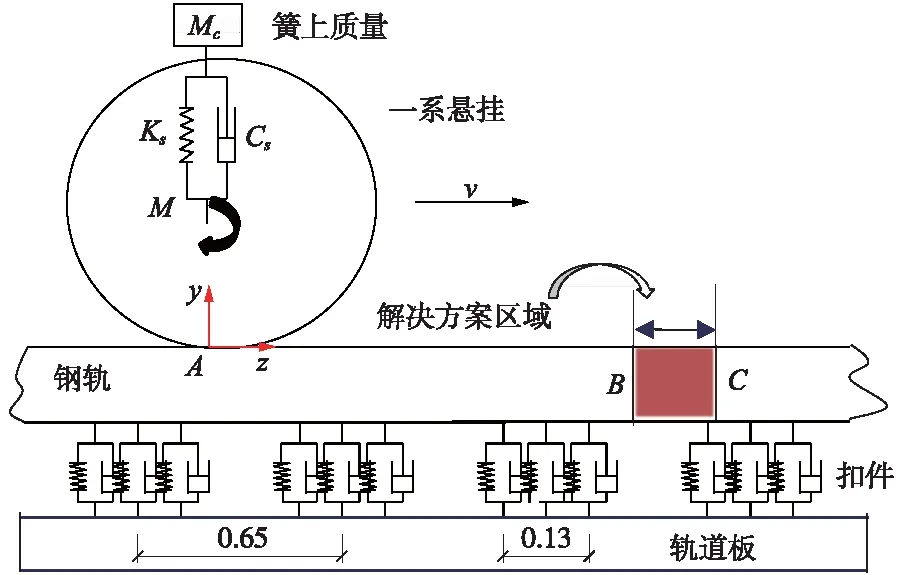
圖1 模型結構示意(單位：m)

除重力荷載外，驅動扭矩是輪軌牽引摩擦接觸模擬中另一個廣泛使用的荷載邊界條件，通常使用梁單元來獲取外部施加的扭矩。如圖2(a)所示，使用4個長度為L的梁單元。每個梁單元由3個節點組成：Ij(j=1，2，3，4)、J和K，其中，K節點定義方向節點。驅動節點J上施加驅動力矩M并垂直于平面S，其方向由右手定則確定，大小按照圖2(b)中施加，大小隨時間線性增加后保持不變。為保證結果可靠，針對輪軌系統的高速動態模擬，通常保證沙漏能量遠小于系統總動能的1%，模型中沙漏系數取為0.001。具體模擬輪軌滾動接觸過程時，通過在輪軸中心施加轉矩M使其保持恒定的速度(“v=300 km/h”)，由圖1所示的初始位置沿著鋼軌向前滾動，經過動態松弛區AB后，系統基本進入穩態滾動狀態，在BC段獲取滾動接觸解。考慮到輪軌瞬態接觸是有關時間的非線性和移動載荷問題，故采用Lagrangian描述進行網格劃分，其中，車輪、鋼軌由8節點六面體單元離散。模型中各材料參數均參照我國某高速線路取值，見表1。

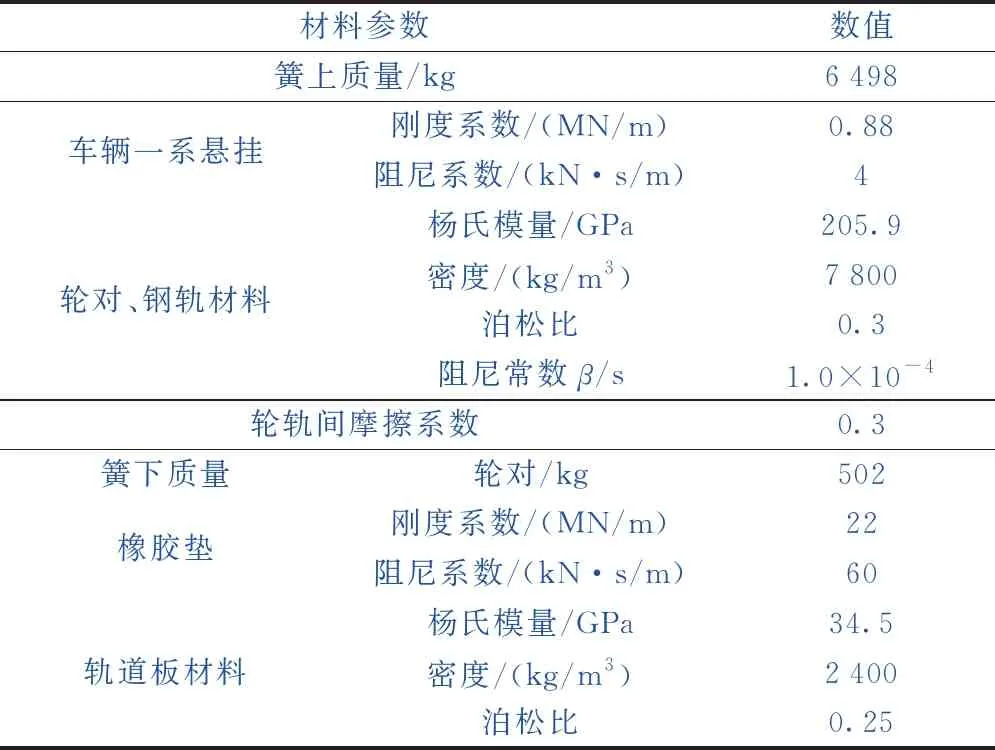
表1 有限元模型材料參數

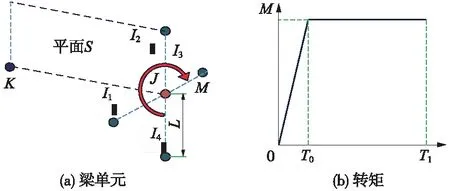
圖2 施加在梁單元上的驅動力矩示意

圖3為不同模型參數條件下的三維輪軌瞬態滾動接觸有限元模型，分別對扣件系統、鋼軌長度、軌道板及全輪對與半輪對的模型結構差異等不同參數進行可控化分析對比，從而探究不同參數條件下對模型瞬態滾動接觸求解的影響。考慮到鋼軌的邊界條件導致數值誤差，圖3(a)中建立的軌道長為15.2 m，鋼軌軌底坡為1∶40。圖3(b)中考慮扣件系統對瞬態接觸計算的影響時，建立含扣件系統鋼軌長度分別為10，15.2，20，50 m的瞬態模型。此外，在考慮軌道板振動特征時，見圖3(c)，其建立全扣件系統軌道長15.2 m，并在扣件下方建立軌道板材料和橡膠墊。圖3(d)在圖3(b)的基礎上建立含扣件系統且軌道長度為15.2 m的全輪對模型，其輪對橫移量為0。

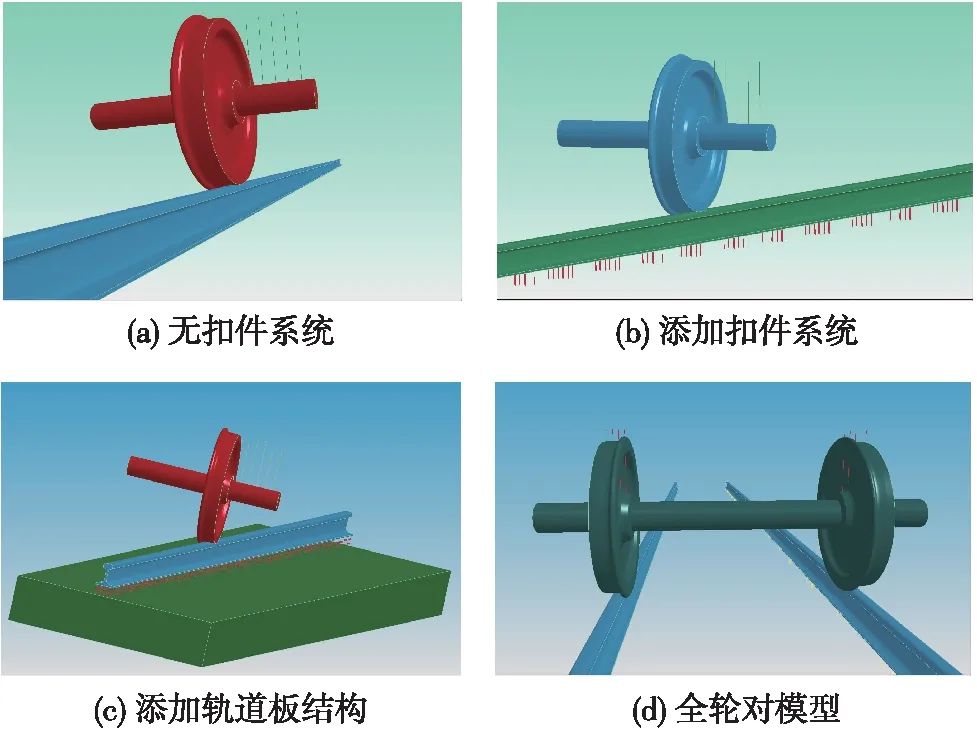
圖3 不同參數條件下的三維輪軌瞬態滾動接觸有限元模型

2 不同參數條件下的輪軌瞬態模型求解分析

圖4給出了不同參數條件下輪軌瞬態滾動接觸模型以300 km/h速度穩態滾過鋼軌時的輪軌垂向力隨時間的變化。

由圖4(a)所示，施加扣件系統的模型，車輪在進入穩態滾動區域時，其動態響應已趨于平穩，輪軌垂向力大小與軸重基本保持一致，大小為68.6 kN，總體呈現周期性波動，對比未施加扣件系統的模型求解結果可知，未添加扣件系統的模型，輪軌力雖然能夠趨于穩定，但是輪軌間的激振作用明顯加大，且在求解瞬態模型計算中，添加扣件系統可使滾動接觸在更短時間內趨于穩定，其實質是扣件系統的阻尼起到了衰減振動的作用，提高了輪軌瞬態滾動接觸的求解效率。由圖4(b)中可知，鋼軌長度并不能影響瞬態模型的計算結果，反而加大鋼軌長度，又造成了數值計算的困難程度，因此，建議模型中鋼軌長度為15 m左右為宜，即24組扣件。

圖4(c)中，施加軌道板結構的模型和未施加軌道板結構的垂向力大小接近。然而存在軌道板結構的時候，其垂向力值更接近于車輪的靜輪載，而且進入穩態計算時，可很好地趨于穩定狀態，垂向力的浮動在5%以內。即存在軌道板結構的時候，輪軌瞬態滾動接觸數值計算會更加精確，可以更好地模擬實際工況。圖4(d)中展示的為半/全輪對的模型結構求解結果對比，全輪對與半輪對在瞬態滾動接觸時，存在橫向約束是否存在的差異，研究對比瞬態接觸垂向力大小可知，右軌的輪軌接觸力明顯大于左軌，這是由于釋放橫向約束后，輪對出現一定橫移量造成的偏差，全輪對模型瞬態解更加能反映出輪軌過渡時的動態響應。

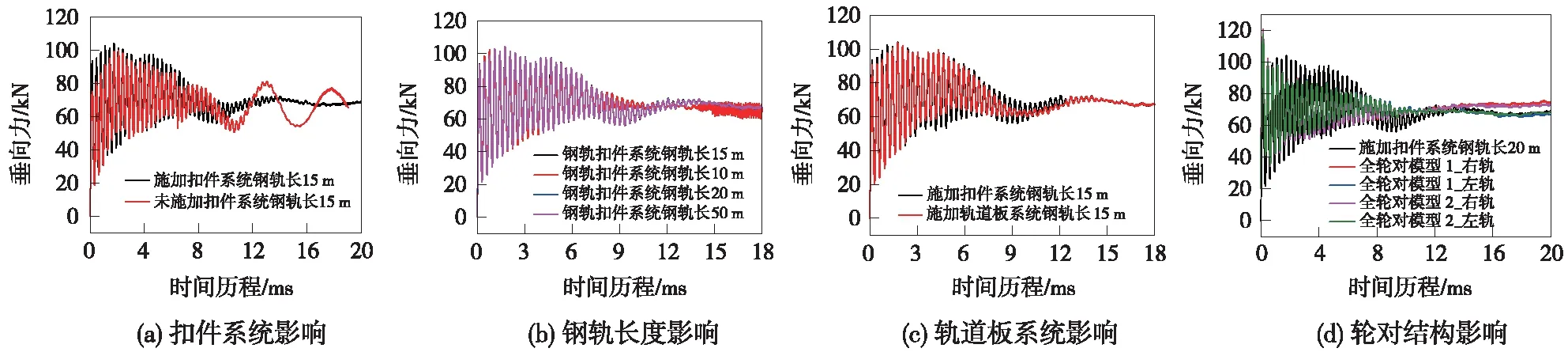
圖4 三維瞬態滾動接觸有限元模型輪軌垂向力

3 三維輪軌瞬態滾動模型沖擊分析

在高速鐵路中，車輪滾動通過時所激發的頻率將導致車輪及鋼軌發生結構上變形，因此，在計算輪軌瞬態滾動接觸之前進行模態分析是必要的。本節選取了實心軸半輪對與全輪對各自的3個典型模態分析結果，分別如圖5和圖6所示。

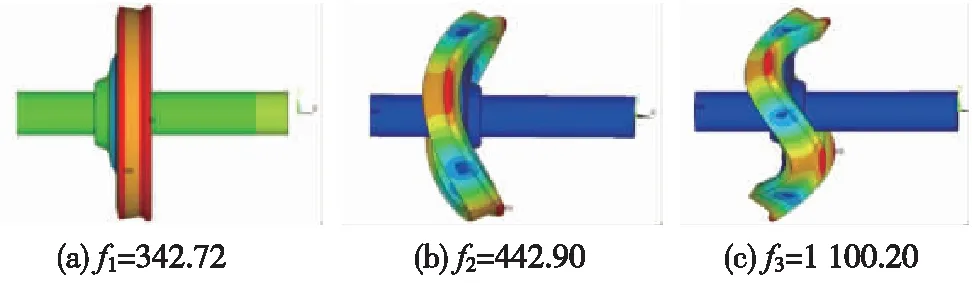
圖5 施加橫向約束的半輪對有限元模態分析(f為激勵頻率，單位:Hz)

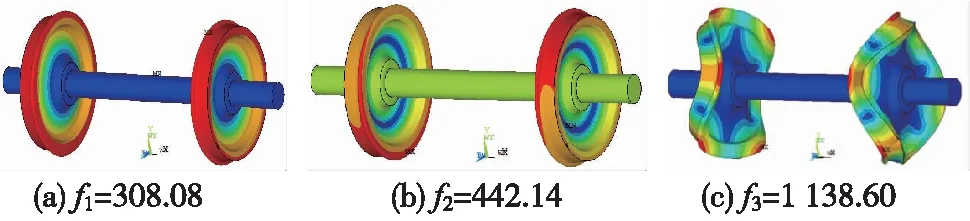
圖6 全輪對有限元模態分析(f為激勵頻率，單位：Hz)

鋼軌軌面不平順是激發高速鐵路輪軌系統高頻振動的激勵源，車輪通過不平順地段時，由于鋼軌表面的不平順，引起輪軌作用力急劇增大，使機車車輛和軌道產生劇烈振動，促使軌道和機車車輛相關部件傷損的產生和發展，從而增加維修費用[20]。基于上述模態分析的結果，對半/全輪對模型鋼軌表面施加凹陷即不平順激勵，使其在輪軌瞬態滾動過程中，能夠激發出對應頻率下的模態變形，見式(1)

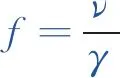
(1)

式中，f為激勵頻率，Hz；v為行車速度，km/h；γ為鋼軌軌面不平順長度，mm。

為方便讀者理解，建立如圖1模型簡圖中的坐標系，OZ為車輪滾動方向，鋼軌表面的不平順施加技術通過自編程序進而修改相應節點坐標值，使得鋼軌缺陷的深度D在縱向和橫向上分別呈余弦和拋物線分布，其對應函數[19]如下

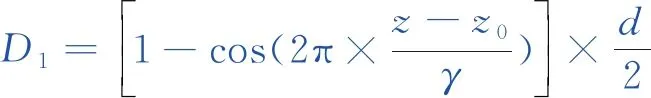
(2)

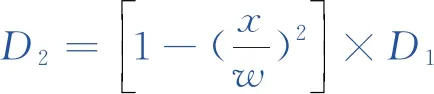
(3)

式中，z0為鋼軌縱向起始位置坐標值；x為鋼軌橫向坐標值；d為鋼軌不平順的最大深度，取0.1 mm；w為鋼軌不平順半寬值30 mm。

圖7為軌面不平順激勵示意。

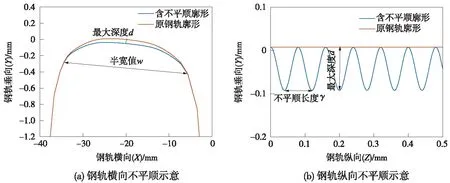
圖7 短波激勵示意

本節模型采用速度300 km/h，不平順參數見表2。結合圖5、圖6對比分析典型半輪對與全輪對模態變形的差異，可以發現，第一組半輪對與全輪對的模態變形一樣，而頻率卻有所差異，半輪對模態為1 100.20 Hz，全輪對模態為1 138.60 Hz；第二組半輪對與全輪對的頻率在442 Hz左右，但其模態變形不一樣；第三組，半輪對模態為342.72 Hz，全輪對模態為308.80 Hz，即半輪對未激發出全輪對相應頻率下的模態，兩者頻率也不同。在實際運營中，鋼軌兩側的不平順狀態幾乎不一致，滾動過程中輪對兩側是相互影響的，于是為分析符合現場的全輪對兩側相互影響下與半輪對建模的瞬態求解差異，將對全輪對一側施加軌面不平順激勵，且半輪對依照全輪對的模態頻率進行施加，以此來分析對比半輪對與全輪對的瞬態求解差異。具體給出了輪軌力大小、最大接觸斑等效應力的結果，如圖8、圖9所示。

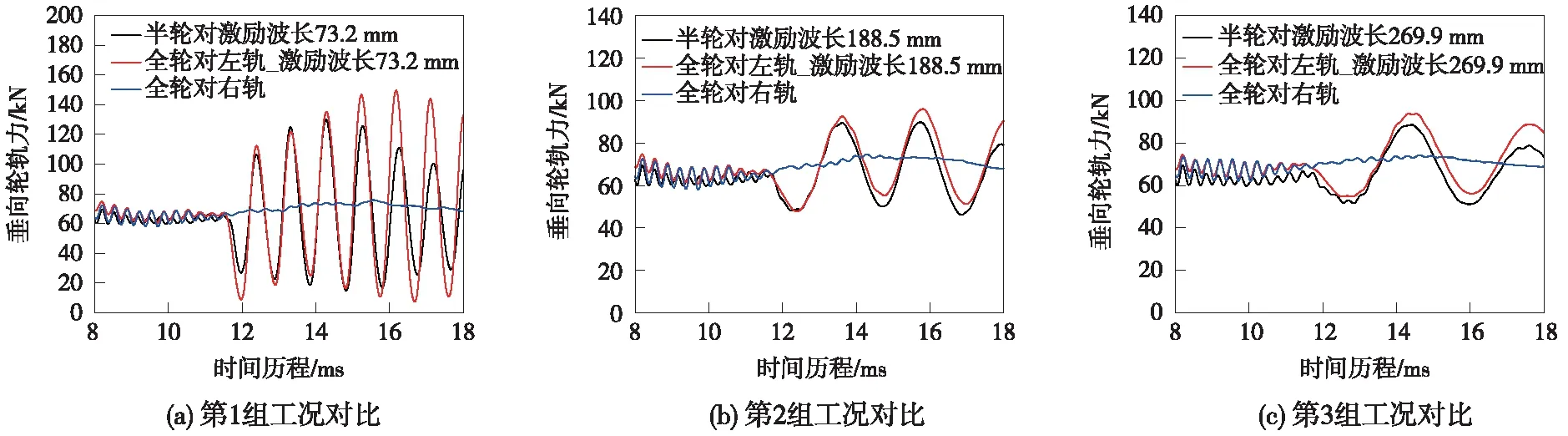
圖8 輪軌滾動接觸垂向力

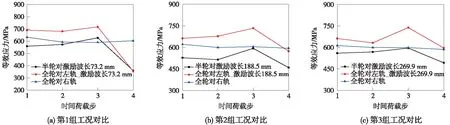
圖9 滾動過程接觸斑內最大等效應力變化趨勢

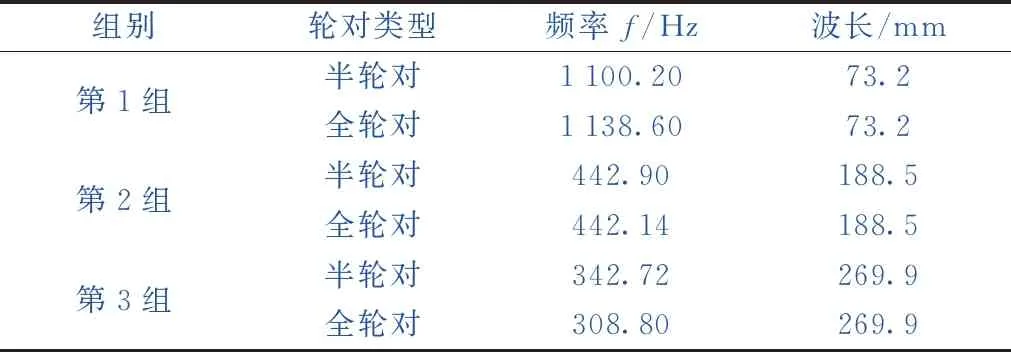
表2 不同模型的鋼軌不平順參數

圖8給出了車輪以300 km/h速度滾動通過鋼軌表面不平順時的輪軌垂向力隨時間的變化，從圖8可以看出，半/全輪對模型在0.011 s時候，開始進入不平順區段，此時輪軌力發生了巨大變化，呈現周期性的正弦形波動，而且峰值也是呈現出先增大后減小的趨勢，相較于穩態計算過程，此時輪軌沖擊作用加劇，原先維持的動態力平衡經過不平順段已經變為更為強烈的振動響應。

通過計算可知，圖8(a)中第1組工況中車輪模態變形一致，而激發的頻率不一致，此時全輪對模型垂向力峰值比半輪對高出15.1%；圖8(b)第2組工況兩者車輪模態變形不一致，頻率保持一致，全輪對左軌垂向力峰值比半輪對高出6.9%；圖8(c)第3組工況半輪對模型未激發出相應的模態變形，而全輪對在此頻率下進行沖擊作用，此時全輪對左軌垂向力比半輪對高出5.8%左右。

上述3組工況中，全輪對模型均發生共振現象，而半輪對未激發出相應的模態，兩者差異明顯，可知半輪對與全輪對之間存在差異，因此在模擬輪軌沖擊的工況下，需建立全輪對模型求解，以保證結果的可靠真實性。值得注意的是，在經過不平順階段，兩種工況的垂向力峰值均呈現出先增大后減小的趨勢，這是因為，此時經過了扣件系統支撐的鋼軌不平順表面，下部結構剛度增大，使得輪軌力出現了些許增加的趨勢，滾過扣件系統時，此時輪軌力會逐漸減小。

圖9給出了車輪滾動通過鋼軌不平順表面的輪軌接觸斑內等效應力大小變化趨勢，可以發現，3種工況中半輪對模型均呈現先平穩過渡然后應力增加再減小的趨勢，而施加有激勵一側的全輪對輪軌間等效應力變化趨勢與之接近，而未施加的則保持平穩過渡。就第1組工況而言，在半輪對車輪經過波峰時應力為628.2 MPa，全輪對車輪經過波峰時應力為717.2 MPa，兩者相差14.2%，半輪對車輪經過波谷時應力為360.8 MPa，全輪對車輪經過波谷時應力為355.7 MPa，兩者相差1.4%，從圖9可知，輪對的沖擊作用更為顯著，另外兩組工況與之規律保持一致。

4 結論與展望

基于三維輪軌瞬態滾動接觸有限元模型，考慮不同模型參數的影響，采用ANSYS/LS-DYNA求解不同條件下車輪通過的瞬態接觸解，詳細對比分析了扣件系統、鋼軌長度、軌道板和建模方式對輪軌瞬態接觸解的影響，并結合模態分析結果，研究半輪對與全輪對的輪軌沖擊效應。結論如下。

(1)扣件系統對輪軌瞬態求解的影響作用顯著，添加扣件系統可使滾動接觸在更短時間內趨于穩定；施加軌道板結構的模型，瞬態數值計算會更加精確，可以更好地模擬實際情況。

(2)結合模態分析結果，對半輪對與全輪對模型施加相同的鋼軌頂面不平順激勵，全輪對模型均發生共振現象，而半輪對未激發出相應的模態，輪軌沖擊過程中兩者差異明顯。因此，在模擬輪軌沖擊工況下，需建立全輪對模型求解，以保證結果的可靠真實性，同時為車輛直線通過行為和模型精細化建立的有效性研究提供了必要的分析手段。

(3)輪軌沖擊響應僅研究了直線段鋼軌不平順所帶來的影響，未考慮到車輪磨耗對輪軌沖擊所帶來的不良隱患。以后的研究工作中，可進一步分析輪對單側及雙側均存在磨耗的情況下，其瞬態輪軌動態響應和輪對間的激勵和傳遞效果。另外，對于車輪次表層裂紋可以同時展開研究，對于實際運營車輛中的車輪璇修問題提供理論支持。