基于DSP的振動(dòng)信號(hào)自適應(yīng)采樣設(shè)計(jì)

吳恩奇 汪國陽 楊振國 段汝良

（浙江中控技術(shù)股份有限公司）

在工業(yè)應(yīng)用中， 旋轉(zhuǎn)機(jī)械設(shè)備必不可少，常見的有汽輪機(jī)、燃?xì)廨啓C(jī)、軸流式壓縮機(jī)、風(fēng)機(jī)及泵等。 由于制造與生產(chǎn)條件所限，這些設(shè)備在旋轉(zhuǎn)工況下會(huì)在各個(gè)方向產(chǎn)生位移，一般轉(zhuǎn)軸徑向位移（也稱其為徑向振動(dòng)）頻率較高［1］。 徑向振動(dòng)的頻率、幅度等參數(shù)可以很好地表征設(shè)備的運(yùn)行狀態(tài)和“健康”狀態(tài)，如通過對振動(dòng)狀態(tài)的分析，可以提前識(shí)別主軸裂紋、轉(zhuǎn)子掉葉等故障，因此在設(shè)備監(jiān)測中起到至關(guān)重要的作用［2］。

工業(yè)領(lǐng)域的大型旋轉(zhuǎn)機(jī)械設(shè)備的振動(dòng)狀態(tài)主要由透平監(jiān)測系統(tǒng)（Turbine Supervisory Instrumentation，TSI）進(jìn)行監(jiān)測、分析與報(bào)警［3］。 TSI系統(tǒng)監(jiān)測的參數(shù)包括振動(dòng)、位移、轉(zhuǎn)速、鍵相及溫度等，其振動(dòng)監(jiān)測功能主要對徑向振動(dòng)波形信號(hào)進(jìn)行時(shí)域分析和頻域分析［4］，其中頻域分析需要進(jìn)行復(fù)雜的快速傅里葉變換 （Fast Fourier Transform，F(xiàn)FT），因此對采樣點(diǎn)數(shù)和采樣頻率有更嚴(yán)格的要求［5］。 為了滿足FFT運(yùn)算要求，常用的方法是延長采樣時(shí)間或?qū)Σ蓸狱c(diǎn)進(jìn)行補(bǔ)零，但這樣處理的結(jié)果也會(huì)使頻域分析很難定位到信號(hào)基頻、2倍頻等，進(jìn)而限制了頻域分析的覆蓋面［6］，會(huì)導(dǎo)致部分故障特性無法識(shí)別。 因此，筆者提出一種具有自適應(yīng)功能的采樣設(shè)計(jì)，基于高速模擬數(shù)字轉(zhuǎn)換器（Analog-to-Digital Converter，ADC）和數(shù)字信號(hào)處理（Digital Signal Processing，DSP）平臺(tái)，運(yùn)用線性插值重采樣方法， 進(jìn)行高采樣頻率的FFT運(yùn)算，實(shí)現(xiàn)設(shè)備的振動(dòng)分析。

1 基本原理概述

1.1 FFT原理

設(shè)復(fù)數(shù)序列x（n）={x（0），x（1），…，x（N-1）}，其離散傅里葉變換（DFT）X（k）為：

由式（1）可知，N點(diǎn)DFT需要做N2次復(fù)數(shù)運(yùn)算。當(dāng)N取值較大時(shí)，DFT需要大量的運(yùn)算次數(shù)，實(shí)際應(yīng)用中對計(jì)算資源和數(shù)據(jù)存儲(chǔ)資源的要求很高［7］。

1.2 重采樣原理

1.2.1 線性插值

線性插值是數(shù)學(xué)和計(jì)算機(jī)領(lǐng)域廣泛使用的一種簡單插值方法［8］。 對于已知點(diǎn)（x0，y0）和（x1，y1），區(qū)間［x0，x1］內(nèi)x對應(yīng)的函數(shù)值為：

考慮到采樣頻率足夠高時(shí)兩個(gè)采樣點(diǎn)間隔較小，線性插值已經(jīng)可以滿足設(shè)計(jì)要求；加之其他復(fù)雜插值方法對內(nèi)存空間與硬件計(jì)算性能要求較高，而線性插值算法具有簡單特性，故采用線性插值方法進(jìn)行重采樣。

1.2.2 重采樣

重采樣的目的是在N′個(gè)實(shí)際采樣點(diǎn)數(shù)中，通過線性插值方法，等時(shí)間間隔抽取N點(diǎn)（本項(xiàng)目以N取2 048為例），以順利進(jìn)行FFT運(yùn)算［9］。 在總采樣時(shí)間不變的前提下， 重采樣后采樣點(diǎn)數(shù)改變，采樣頻率隨之改變，并存在以下線性關(guān)系：

其中，fS為重采樣后的采樣頻率，fS′為原始采樣頻率。

如果總采樣時(shí)間改變， 則fS與fS′將不存在線性關(guān)系，導(dǎo)致fS不能被準(zhǔn)確計(jì)算［9］。所以，重采樣過程存在一個(gè)約束條件，即首尾兩個(gè)數(shù)據(jù)點(diǎn)必須保留，以保證總采樣時(shí)間不變。

數(shù)據(jù)點(diǎn)插值示意圖如圖1所示， 為滿足約束條件，在每兩點(diǎn)間插值2 046個(gè)，則總點(diǎn)數(shù)M=（N′-1）×2046+N′=2047N′-2046。第0點(diǎn)被保留，則剩余2047（N′-1）點(diǎn)，每（N′-1）點(diǎn)取最后1點(diǎn)，加上第0點(diǎn)則剛好抽取2 048點(diǎn)，且首尾兩點(diǎn)均被保留。

圖1 數(shù)據(jù)點(diǎn)插值示意圖

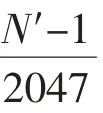
圖2 插值后總點(diǎn)數(shù)示意圖

對于i=0～2047，有下式成立：

得到商ai余bi，那么線性插值點(diǎn)位置是實(shí)際采樣點(diǎn)ai與ai+1之間的第bi點(diǎn)， 根據(jù)線性插值公式，有：

2 自適應(yīng)采樣實(shí)現(xiàn)

2.1 被測對象說明

如圖3所示， 振動(dòng)信號(hào)①由旋轉(zhuǎn)機(jī)械的振動(dòng)傳感器產(chǎn)生［10］，鍵相信號(hào)②由鍵相傳感器產(chǎn)生并經(jīng)電路調(diào)理所得［11］，其一個(gè)脈沖代表機(jī)械轉(zhuǎn)軸轉(zhuǎn)動(dòng)一周，采樣時(shí)由DSP捕獲鍵相信號(hào)②，在其下降沿③對振動(dòng)信號(hào)①進(jìn)行采樣，經(jīng)過相應(yīng)周期后在其下降沿③結(jié)束采樣，其中每兩個(gè)相鄰下降沿之間即1個(gè)整周期④。 鍵相信號(hào)的作用：一是DSP對其進(jìn)行捕獲，計(jì)算轉(zhuǎn)軸轉(zhuǎn)速；二是DSP在鍵相信號(hào)下降沿開始采樣并在相應(yīng)周期后的下降沿結(jié)束采樣，保證振動(dòng)信號(hào)的整周期采樣［12］。

圖3 振動(dòng)信號(hào)采樣示意圖

2.2 數(shù)采硬件拓?fù)?/h3>

筆者設(shè)計(jì)的數(shù)采硬件平臺(tái)主要由高速ADC與DSP構(gòu)成。 為了保證較高的采樣頻率與采樣精度，設(shè)計(jì)選用采樣率達(dá)百kSPS的∑-ΔADC［13］。FFT運(yùn)算要求數(shù)據(jù)點(diǎn)數(shù)為2的整數(shù)次冪， 點(diǎn)數(shù)越多頻譜分析的分辨率越小，精度就越高。 本項(xiàng)目取常見的2 048點(diǎn)（16位），則一組原始數(shù)據(jù)與重采樣后數(shù)據(jù)將占用十幾KB內(nèi)存，考慮到RAM對DSP價(jià)格影響較大 （以TI公司C2000系列為例，RAM增加1倍價(jià)格也大致增加1倍）， 因此選取幾十KB RAM即可。由于ADC采樣頻率較高，則要求后級(jí)DSP有較強(qiáng)的運(yùn)算能力，以避免數(shù)據(jù)處理慢而導(dǎo)致前后級(jí)不匹配的問題，因此選用計(jì)算速率達(dá)到百M(fèi)IPS的DSP［14］。

基于DSP的振動(dòng)信號(hào)自適應(yīng)數(shù)采硬件拓?fù)淙鐖D4所示，振動(dòng)信號(hào)由傳感器產(chǎn)生，經(jīng)卡件調(diào)理電路后由ADC進(jìn)行模數(shù)轉(zhuǎn)化， 最后由DSP根據(jù)鍵相信號(hào)進(jìn)行采樣，并做數(shù)據(jù)處理。

圖4 數(shù)采硬件拓?fù)涫疽鈭D

2.3 采樣方案

DSP內(nèi)部采樣流程如圖5所示。 首先，DSP對鍵相信號(hào)進(jìn)行捕獲，計(jì)算信號(hào)頻率，根據(jù)預(yù)設(shè)分段頻率確定采樣周期數(shù)n。 然后，DSP在鍵相信號(hào)下降沿對振動(dòng)數(shù)字信號(hào)整周期采樣，并對采樣數(shù)據(jù)進(jìn)行線性插值重采樣，將得到的2 048個(gè)數(shù)據(jù)點(diǎn)進(jìn)行FFT運(yùn)算。 最后，計(jì)算得到振動(dòng)信號(hào)0.5倍頻、基頻與2倍頻的幅值，根據(jù)工業(yè)應(yīng)用要求，幅值精度須達(dá)到±1%。

圖5 振動(dòng)信號(hào)采樣流程示意圖

2.3.1 采樣周期數(shù)確定

采樣數(shù)據(jù)經(jīng)FFT運(yùn)算后， 得到相應(yīng)頻率點(diǎn)的幅值，將其描繪成圖（即幅頻譜圖）。 頻域分析精度主要取決于兩個(gè)方面： 一是FFT運(yùn)算后目標(biāo)頻率是否被準(zhǔn)確定位； 二是頻譜分辨率是否足夠高。

設(shè)ADC硬件采樣頻率為fADC、 信號(hào)基頻為fB，則實(shí)際采樣數(shù)據(jù)點(diǎn)N′的計(jì)算式為：

從N′個(gè)實(shí)際采樣點(diǎn)中插值抽取N點(diǎn)， 則真實(shí)信號(hào)采樣頻率fS的計(jì)算式為：

由此可得FFT頻譜分辨率為：

那么，對于頻譜任一點(diǎn)Z（Z≤N，且Z為整數(shù)），其頻率fZ的計(jì)算式為：

因此，頻譜分辨率只與fB和n有關(guān)。 如果n取整數(shù)，那么信號(hào)基頻一定能被準(zhǔn)確定位。 至于分辨率，由于最小需要分析到信號(hào)0.5倍頻，則n≥2即可。所以，為了準(zhǔn)確定位到信號(hào)的0.5倍頻、基頻與2倍頻，取n≥2且n為整數(shù)即可。

由上述分析可知，n取值越大，頻譜分辨率越小，分析結(jié)果越精確，但N′也越多。 由于DSP的內(nèi)存所限，N′不能無限增加。 由于實(shí)際內(nèi)存為幾十KB且抽取點(diǎn)數(shù)為2 048，因此將N′約束在8 192點(diǎn)以內(nèi)即可。ADC最大采樣頻率設(shè)定為62.5 kHz，根據(jù)式（7）可得信號(hào)頻率與采樣周期數(shù)的關(guān)系，詳見表1。

從表1可以看出，當(dāng)信號(hào)頻率不斷減小，為了保證N′在約束條件以內(nèi)，n也不斷減小；但n取最小值2后信號(hào)頻率仍不斷減小，此時(shí)已不能通過減小n的值來控制N′。 為了在低速時(shí)仍然能夠進(jìn)行采樣并準(zhǔn)確分析，只能通過降低硬件采樣頻率fADC來滿足約束條件。 對工業(yè)應(yīng)用的調(diào)研結(jié)果顯示，單事件轉(zhuǎn)速在60 r/min以下一般不需要監(jiān)測振動(dòng)狀態(tài)，故將最小頻率定在1 Hz。 在中高轉(zhuǎn)速下，實(shí)際采樣點(diǎn)數(shù)在4 000～8 000；在低轉(zhuǎn)速下，實(shí)際采樣點(diǎn)數(shù)在3 906～7 812，都能滿足N′的約束條件。

表1 信號(hào)頻率與采樣周期數(shù)對應(yīng)表

DSP捕獲到鍵相信號(hào)并計(jì)算信號(hào)頻率后，與表1數(shù)據(jù)進(jìn)行對比，從而確定采樣周期數(shù)，根據(jù)鍵相信號(hào)，下降沿采樣n個(gè)周期。

2.3.2 采樣頻率分析

根據(jù)香農(nóng)定理， 采樣頻率必須不小于2倍的信號(hào)所包含的最大頻率，才能包含原信號(hào)的所有真實(shí)信息［15］。 若采樣頻率不滿足該約束條件，原始信息不能被完全采集，那么頻域分析結(jié)果將存在較大誤差，因此采樣頻率對本設(shè)計(jì)的精度有重大影響，根據(jù)式（8）將表1數(shù)據(jù)代入可得信號(hào)頻率與采樣頻率對應(yīng)表（表2）。

表2 信號(hào)頻率與采樣頻率對應(yīng)表kHz

本設(shè)計(jì)頻域分析范圍最大到信號(hào)的2倍頻，即分析的最大頻率是信號(hào)頻率的2倍。 根據(jù)香農(nóng)采樣定理和表2可知，采樣頻率遠(yuǎn)大于4倍的信號(hào)頻率，所以采樣后的信號(hào)不會(huì)失真，保證頻域分析得到的結(jié)果包含了所有真實(shí)信息。

3 仿真驗(yàn)證

3.1 采樣方法對比驗(yàn)證

本測試是在DSP內(nèi)部用純算法模擬完成的。DSP生成仿真振動(dòng)信號(hào)， 采用不同方法對仿真振動(dòng)信號(hào)進(jìn)行采樣并進(jìn)行FFT運(yùn)算， 對比其頻域分析的頻率與幅值精度。

采用以下3種不同的采樣方法：

a. 延長采樣時(shí)間——定點(diǎn)采樣8 192點(diǎn)做FFT運(yùn)算；

b. 補(bǔ)零——實(shí)際采樣點(diǎn)數(shù)與本設(shè)計(jì)相同，對采樣點(diǎn)進(jìn)行補(bǔ)零，使采樣點(diǎn)數(shù)達(dá)到2的整數(shù)次冪；

c. 本設(shè)計(jì)方法——多周期采樣，線性插值重采樣。

為了對比信號(hào)的0.5倍頻、基頻與2倍頻，仿真信號(hào)包含3種成比例的頻率。 測試對比3種方法頻域分析后的頻率與幅值精度， 詳見表3， 可以看出，定點(diǎn)數(shù)采樣與補(bǔ)零方法都不能準(zhǔn)確定位到信號(hào)0.5倍頻、基頻與2倍頻，頻域分析得到的頻率與信號(hào)存在一定偏差，且該偏差隨信號(hào)頻率變化而變化，不能控制在一定范圍內(nèi)。 頻率的偏差導(dǎo)致幅值存在較大誤差， 僅3次測試最大相對誤差即高達(dá)-36%（仿真信號(hào)2， 補(bǔ)零方法， 基頻幅值，（0.1591-0.25）/0.25=-36.36%）。 而本設(shè)計(jì)完全可以準(zhǔn)確定位，頻率不存在偏差，幅值的相對誤差均在±0.3%，相較于前兩種方法有明顯改善。

表3 模擬振動(dòng)信號(hào)頻域分析結(jié)果對比

為了使結(jié)果更直觀， 將運(yùn)算數(shù)據(jù)在MATLAB以頻譜圖形式呈現(xiàn)［16］，如圖6所示，其中仿真信號(hào)為y =0.25sin （2π ×150 ×t） +sin （2π ×300 ×t） +0.25sin（2π×600×t）。 從圖6可以看出，定點(diǎn)數(shù)采樣方法和補(bǔ)零方法的頻譜圖存在其他頻率分量的干擾，定點(diǎn)數(shù)采樣頻譜圖的目標(biāo)頻率附近分量有較大幅值，補(bǔ)零頻譜圖則分布著較多起伏的頻率分量； 本設(shè)計(jì)則基本消除了干擾頻率的影響，頻譜圖呈現(xiàn)出目標(biāo)頻率幅值大、干擾頻率幅值極小的理想圖像。

圖6 3種方法運(yùn)算數(shù)據(jù)在MATLAB的頻譜圖

綜上，相比于目前常見的方法，本設(shè)計(jì)有著明顯的優(yōu)勢，極大提升了振動(dòng)信號(hào)頻域分析的精度。

3.2 采樣精度驗(yàn)證

為了驗(yàn)證本設(shè)計(jì)分析結(jié)果的精度，分析仿真振動(dòng)信號(hào)，得到相應(yīng)頻率與幅值的分析結(jié)果（表4），可以看出，本設(shè)計(jì)頻率不存在誤差，0.5倍頻、基頻與2倍頻幅值最大相對誤差分別為全量程的±0.03%、±0.10%與±0.11%，相對誤差在本設(shè)計(jì)±0.3%精度之內(nèi)。

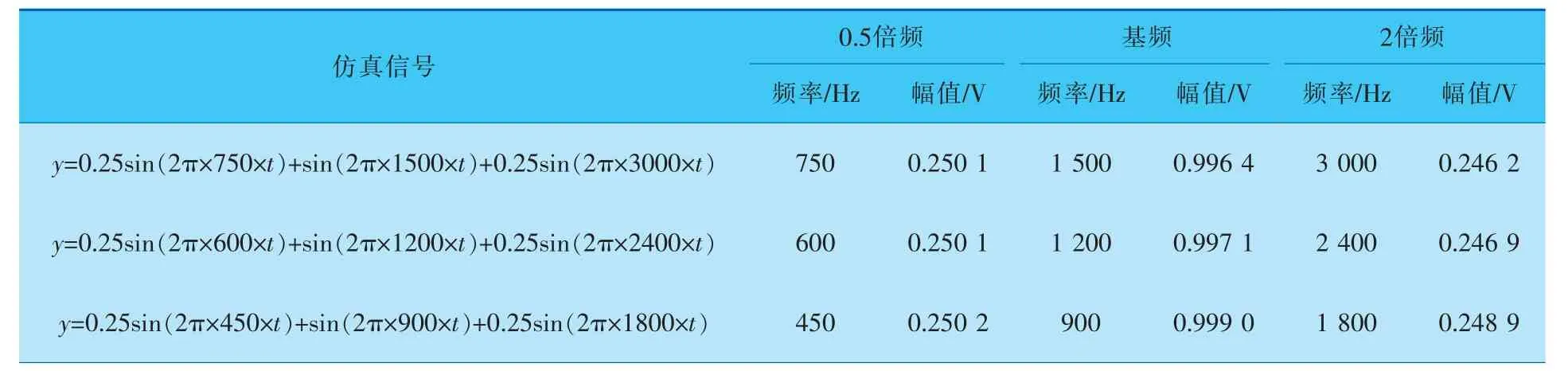
表4 模擬振動(dòng)信號(hào)頻域分析結(jié)果

（續(xù)表4）

綜上，本設(shè)計(jì)得到的頻率與幅值精度均達(dá)到了設(shè)計(jì)目標(biāo)。

4 結(jié)束語

筆者提出的技術(shù)方案主要針對大型旋轉(zhuǎn)機(jī)械設(shè)備振動(dòng)信號(hào)的采樣與分析，在目前常用采樣方法精度不高的背景下，采用基于線性插值重采樣的自適應(yīng)采樣方案，在保持高采樣頻率的前提下，有效控制實(shí)際采樣點(diǎn)數(shù)，無需占用太多硬件內(nèi)存，實(shí)現(xiàn)了基于硬件平臺(tái)的頻域分析。 此外，本設(shè)計(jì)可準(zhǔn)確定位到信號(hào)0.5倍頻、基頻與2倍頻，使FFT運(yùn)算后的結(jié)果誤差最小。 仿真結(jié)果證實(shí)了本設(shè)計(jì)能夠進(jìn)行復(fù)雜信號(hào)的采樣與分析，且精度相對于常見方法有顯著提升， 滿足工業(yè)應(yīng)用需求。本設(shè)計(jì)可應(yīng)用于監(jiān)測旋轉(zhuǎn)設(shè)備的振動(dòng)狀態(tài)，為旋轉(zhuǎn)設(shè)備的高精度振動(dòng)分析提供技術(shù)參考。