基于近似最小一乘準(zhǔn)則的Hammerstein-Wiener模型隨機(jī)梯度辨識(shí)

徐寶昌 榮志超 王雅欣 董秀娟 許立偉

（1.中國(guó)石油大學(xué)（北京）信息科學(xué)與工程學(xué)院；2.國(guó)家管網(wǎng)集團(tuán)北京管道有限公司）

日益復(fù)雜的化工過(guò)程中存在大量的非線性過(guò)程， 線性模型對(duì)工業(yè)過(guò)程的描述能力有限，采用非線性模型描述化工過(guò)程，其高質(zhì)量的建模結(jié)果可直接提升化工生產(chǎn)過(guò)程的控制品質(zhì)［1～5］。典型的非線性Hammerstein-Wiener（H-W）模型較適合表示化工過(guò)程中的大多數(shù)非線性過(guò)程。

H-W模型是一種塊連接模型，這種通過(guò)組合線性動(dòng)態(tài)模塊和非線性靜態(tài)模塊的塊連接結(jié)構(gòu)模型能夠有效地限制模型的靈活性［6～10］。 H-W模型已經(jīng)成功應(yīng)用到一些實(shí)際過(guò)程中，例如太陽(yáng)能電池板［11］、聚合酶反應(yīng)器［12］、地埋管換熱器［13］、燃料電池反應(yīng)控制系統(tǒng)［14］及催化系統(tǒng)［15］等。 針對(duì)HW模型的辨識(shí)，Bai E W提出了兩階段辨識(shí)算法和盲辨識(shí)算法［16，17］；Zhu Y C提出了松弛迭代法［18］；Park H C等提出用4種特殊信號(hào)順序辨識(shí)H-W模型［19］；李妍等提出了一種改進(jìn)偏差補(bǔ)償辨識(shí)算法［20］；Xu K K等基于極限學(xué)習(xí)機(jī)對(duì)H-W模型進(jìn)行了辨識(shí)［21］。 這些算法針對(duì)相應(yīng)的H-W模型都能成功進(jìn)行參數(shù)辨識(shí)，但也都存在一定的問(wèn)題［22～25］，例如：盲辨識(shí)算法沒(méi)有顯式考慮廣泛存在于實(shí)際過(guò)程中的噪聲；兩階段辨識(shí)法和松弛迭代法的計(jì)算量都過(guò)大；特殊信號(hào)法在實(shí)際應(yīng)用中很難使用人為設(shè)計(jì)的信號(hào)；極限學(xué)習(xí)機(jī)很大程度上依賴于初始值。 同時(shí)，目前關(guān)于H-W模型的辨識(shí)算法推導(dǎo)過(guò)程大多基于最小二乘準(zhǔn)則，但是當(dāng)隨機(jī)噪聲不滿足正態(tài)分布（系統(tǒng)存在尖峰噪聲或異常點(diǎn)）時(shí)，由于其目標(biāo)函數(shù)中的平方項(xiàng)，數(shù)據(jù)存在很小的改變都會(huì)引起較大的波動(dòng)，對(duì)辨識(shí)結(jié)果產(chǎn)生很大的影響［26，27］。

針對(duì)上述問(wèn)題， 筆者提出一種形式簡(jiǎn)單、易于計(jì)算并且更近似絕對(duì)值函數(shù)的新型確定性可導(dǎo)函數(shù)，構(gòu)造近似最小一乘準(zhǔn)則目標(biāo)函數(shù)，在此基礎(chǔ)上推導(dǎo)基于近似最小一乘準(zhǔn)則的隨機(jī)梯度辨識(shí)（Stochastic Gradient Algorithm Based on Approximate Least Absolute Deviation Criterion，ALADSG）算法。仿真實(shí)驗(yàn)表明，ALADSG算法可以有效克服尖峰噪聲對(duì)辨識(shí)結(jié)果的影響，其辨識(shí)精度高、收斂速度快并且具有良好的魯棒性。

1 H-W模型描述

H-W模型的結(jié)構(gòu)如圖1所示，其中，g［·］和h［·］分別為系統(tǒng)的輸入和輸出非線性模塊，設(shè)輸出非線性模塊h［·］可逆；G（z）是系統(tǒng)的動(dòng)態(tài)線性模塊；u（k）是系統(tǒng)的輸入信號(hào)；x（k）是輸入非線性模塊的輸出，也是線性模塊的輸入；w（k）是線性模塊的輸出，也是輸出非線性模塊的輸入；r（k）是系統(tǒng)的真實(shí)輸出，與噪聲項(xiàng)v（k）疊加后得到系統(tǒng)的測(cè)量輸出y（k）。

圖1 H-W模型結(jié)構(gòu)框圖

H-W模型輸出可以改寫為：

模型參數(shù)為：

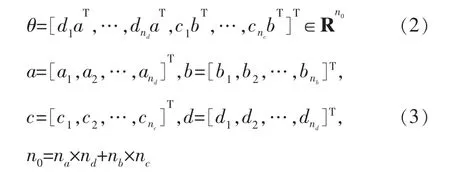
觀測(cè)數(shù)據(jù)矩陣為：

其中，φ（k）是觀測(cè)數(shù)據(jù)矩陣；θ是待辨識(shí)參數(shù)矩陣；a、b、c、d是待辨識(shí)參數(shù)；n是階次；ψ（k）是輸出模塊觀測(cè)矩陣；φ（k）是輸入模塊觀測(cè)矩陣；gs和hl分別代表輸入模塊、輸出模塊的多項(xiàng)式。

可以觀察到在待辨識(shí)參數(shù)矩陣θ中含有組合參數(shù)，為了便于參數(shù)分離，令c1和d1已知，采用平均值法進(jìn)行參數(shù)ci和di的分離［28］。

2 ALADSG算法

文獻(xiàn)［29］提出了如下的對(duì)數(shù)函數(shù)近似絕對(duì)值函數(shù)：

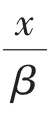
采用另一種絕對(duì)值函數(shù)的光滑近似函數(shù)［30］：

其中，μ是可控參數(shù)，當(dāng)μ比較小時(shí)，可有效地等價(jià)為絕對(duì)值函數(shù)，本研究中取μ=0.01。

將f1（x）和f2（x）同時(shí)減去絕對(duì)值函數(shù)｜x｜，x取不同區(qū)間時(shí)的相對(duì)誤差見表1。

表1 x取不同區(qū)間時(shí)的相對(duì)誤差

由表1可得，函數(shù)f2（x）更接近絕對(duì)值函數(shù)，并且形式簡(jiǎn)單、計(jì)算量更小。 因此，筆者基于函數(shù)f2（x）構(gòu)造近似最小一乘準(zhǔn)則。

取目標(biāo)函數(shù)：

根據(jù)隨機(jī)梯度搜索原理可得：

其中，收斂因子μk>0。

將式（12）代入式（13）可得：

將式（14）代入式（11）可得：

其中，e（k）代表新息。

令：

根據(jù)式（17）、（18）極小化h（μk）可得最優(yōu)解：

將μk代入式（14）可得：

令：

考慮對(duì)過(guò)去數(shù)據(jù)的遺忘性，為了加快收斂速度同時(shí)提高算法精度，引入遺忘因子λ，則有：

式（21）、（23）構(gòu)成帶有遺忘因子的基于近似最小一乘準(zhǔn)則的隨機(jī)梯度辨識(shí)算法， 與選取式（9）作為目標(biāo)函數(shù)得到的算法進(jìn)行運(yùn)算速度的對(duì)比，均進(jìn)行30萬(wàn)次迭代，得到的結(jié)果見表2。

表2 兩種算法的運(yùn)算時(shí)間對(duì)比ms

由表2可得，基于式（10）推導(dǎo)的隨機(jī)梯度算法相較于基于式（9）推導(dǎo)的隨機(jī)梯度算法計(jì)算量更少，速度提升約5.7%。

3 仿真實(shí)驗(yàn)

Park H C等研究的pH中和系統(tǒng)［19］如圖2所示，V代表容積，其中濃度為0.02 mol/L 的醋酸（CH3COOH） 作為輸入流在連續(xù)攪拌釜反應(yīng)器中通過(guò)濃度為0.5 mol/L的氫氧化鈉（NaOH）滴定流進(jìn)行滴定。 滴定流分為vm和v，vm為恒定的，v由計(jì)算機(jī)信號(hào)u調(diào)節(jié)。

圖2 pH中和系統(tǒng)

該pH中和過(guò)程可近似建模為H-W模型，其中x（k）和w（k）分別表示為［19］：

線性模塊傳遞函數(shù)為：

為進(jìn)行參數(shù)分離，令參數(shù)c1和d1已知。

3.1 不同遺忘因子的ALADSG算法

在模型辨識(shí)過(guò)程中加入尖峰噪聲概率為5%、幅值為白噪聲序列5倍的尖峰序列噪聲， 不同遺忘因子的H-W模型的參數(shù)辨識(shí)結(jié)果見表3，相對(duì)誤差曲線如圖3所示。

圖3 不同λ的相對(duì)誤差曲線

表3 不同λ取值的H-W模型參數(shù)辨識(shí)結(jié)果

根據(jù)表3和圖3可以得到如下結(jié)論：當(dāng)λ=1時(shí)，即不引入遺忘因子，算法的辨識(shí)結(jié)果較差，無(wú)法估計(jì)出H-W模型的參數(shù)。當(dāng)0.7<λ＜0.9時(shí)，隨著遺忘因子λ的減小，δ下降的速度更快，同時(shí)辨識(shí)相對(duì)誤差更接近于0，即辨識(shí)的速度更快，精度也更高。 當(dāng)λ≤0.5時(shí)，相對(duì)誤差曲線開始波動(dòng)，最終辨識(shí)結(jié)果的精度也已開始下降。 所以不能一味減小λ來(lái)尋求更快的辨識(shí)速度，而要兼顧精度與穩(wěn)定性。

3.2 ALADSG算法與LSSG算法對(duì)比

由3.1節(jié)可知，當(dāng)λ=0.8時(shí)，辨識(shí)可以在保證穩(wěn)定性的前提下收斂，較為準(zhǔn)確地估計(jì)出H-W模型參數(shù)，故本節(jié)固定遺忘因子λ=0.8。

為驗(yàn)證ALADSG算法的辨識(shí)性能， 分別加入不同概率和幅值的尖峰噪聲，同時(shí)加入基于最小二乘準(zhǔn)則的隨機(jī)梯度算法 （Stochastic Gradient Algorithm Based on Least Square Criterion，LSSG）作為對(duì)比進(jìn)行實(shí)驗(yàn)。 令ε表示尖峰噪聲概率，A表示尖峰噪聲幅值相對(duì)于白噪聲幅值的倍數(shù)。 在不加入尖峰噪聲，加入ε=5%、A=5的尖峰噪聲，加入ε=10%、A=10的尖峰噪聲，3種情況下得到的仿真結(jié)果見表4，對(duì)應(yīng)的相對(duì)誤差曲線如圖4所示。

圖4 加入不同尖峰噪聲時(shí)的相對(duì)誤差曲線

表4 不同尖峰噪聲時(shí)的仿真結(jié)果

從表4和圖4可知，當(dāng)辨識(shí)過(guò)程中僅存在白噪聲時(shí)， 兩種算法都能準(zhǔn)確估計(jì)出模型參數(shù)，但LSSG算法的速度更快，精度更高。因此，當(dāng)干擾噪聲服從正態(tài)分布時(shí)，LSSG算法性能優(yōu)于ALADSG算法，符合以往的研究結(jié)論。 在辨識(shí)過(guò)程中加入尖峰序列后，LSSG算法受尖峰噪聲影響較大，辨識(shí)精度明顯下降，當(dāng)尖峰噪聲概率ε和幅值A(chǔ)較大時(shí)已不能精確辨識(shí)； 而ALADSG算法受尖峰噪聲影響較小，仍然可以保持較高的辨識(shí)精度。 說(shuō)明在存在尖峰噪聲的情況下，ALADSG算法性能優(yōu)于LSSG算法。

4 結(jié)束語(yǔ)

H-W模型能夠有效擬合化工過(guò)程中的大多數(shù)非線性過(guò)程，且能限制模型的靈活性，避免過(guò)擬合的問(wèn)題。 但當(dāng)模型辨識(shí)過(guò)程中存在尖峰噪聲時(shí)，傳統(tǒng)辨識(shí)方法不能進(jìn)行有效辨識(shí)。 筆者針對(duì)該問(wèn)題提出了ALADSG算法。 采用一種確定性可導(dǎo)函數(shù)近似最小一乘準(zhǔn)則，解決了最小一乘準(zhǔn)則函數(shù)不可求導(dǎo)的問(wèn)題，降低了計(jì)算量。 仿真結(jié)果表明， 相較于LSSG算法，ALADSG算法能夠有效克服尖峰噪聲對(duì)H-W模型辨識(shí)結(jié)果的影響，提高了辨識(shí)結(jié)果的精度并具有良好的魯棒性，降低了辨識(shí)算法對(duì)測(cè)量數(shù)據(jù)質(zhì)量的要求。 同時(shí)，選擇合適的遺忘因子可以增加辨識(shí)結(jié)果的精度、加快收斂速度。