含腐蝕缺陷的非粘結柔性管骨架層承載分析*

魯中歧 崔俊國 肖文生 王魁濤 張 俊

(1.中國石油大學(華東)機電工程學院 2.中海油研究總院有限責任公司)

0 引 言

腐蝕缺陷嚴重影響了油氣管道的承載能力，進而影響其運載壽命。目前，國內外學者針對腐蝕缺陷形貌尺寸對傳統剛性管道承載能力影響關系進行了深入研究，其中部分專家借助數值分析軟件建立了管道有限元模型，對矩形和球形等不同形狀的單個腐蝕缺陷進行了模擬，分析了腐蝕形貌對管道失效壓力的影響[1]；不少學者也對腐蝕缺陷的長度、寬度及徑向深度對管道承載能力的影響規律進行了研究，得出了腐蝕缺陷深度對管道失效壓力影響最大、缺陷長度次之、缺陷寬度影響最小的結論[2-4]。還有一些研究人員對存在軸向、環向及交疊等情況的組合腐蝕缺陷對管道等效應力的影響規律進行了探討，得出結論如下：軸向及環向存在多個腐蝕坑時，存在一個臨界距離，大于該臨界距離時，兩腐蝕缺陷不會相互影響；對于交疊分布缺陷，小缺陷對等效應力的影響不可忽略[5-7]。

以上研究都是針對于傳統剛性管，而柔性管道相比剛性管道具有更大的優勢，逐步得到廣泛應用。柔性管最內層骨架層與運輸介質直接接觸，不可避免地會有腐蝕發生，進而影響管道的承壓能力，導致管道失效。然而針對該腐蝕缺陷對于管道承載能力影響規律的研究還比較少。國內外相關專家通過數值分析的方法，探討了材料非線性、初始橢圓度、相鄰節之間的接觸方式及螺旋纏繞角度等因素對均勻荷載或對徑向壓力下的骨架層失效壓力的影響，得出了材料非線性對骨架層的抗壓潰能力影響最大，初始橢圓度及接觸方式影響次之，螺旋纏繞角度影響最小的結論[8-13]。

上述針對柔性管骨架層的研究都在無腐蝕缺陷情況下進行，有關腐蝕缺陷對非粘結柔性管骨架層的承壓能力研究較少。為此，筆者結合已有研究成果，借用ANSYS Workbench軟件建立了柔性管骨架層的有限元模型，研究了腐蝕形貌尺寸及腐蝕形式對骨架層失效壓力的影響規律，并借助分析結果對骨架層的腐蝕狀態進行了劃分。研究結果可為柔性管腐蝕程度評價提供借鑒。

1 理論模型研究

圓環在均勻外壓載荷下的屈曲載荷值[8]可結合鐵木辛柯彈性穩定理論中圓環撓曲線微分方程推導，具體如下：

(1)

(2)

式中：q為圓環均勻外壓下的屈曲載荷，MPa;I為圓環矩形截面慣性矩，m3;b為矩形截面長，m;t為矩形截面寬，m;R為圓環半徑，m;E為材料彈性模量,MPa。

對于傳統均質圓環，截面為長方形，于是單位長度下的平面應力臨界壓潰值qcr為：

(3)

由于非粘結柔性管骨架層截面形狀十分復雜，可依據下式計算等效厚度teq：

(4)

式中：IGmin為骨架層截面的最小主慣性矩，m4;A為截面面積,m2。

本文選取內徑101.6 mm(4 in)非粘結柔性管道為研究對象，骨架層截面尺寸如圖1所示[14]。

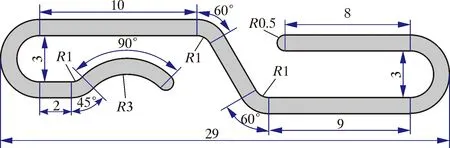
圖1 骨架層截面

該骨架層截面面積A為56.210 7 mm2，最小主慣性矩IGmin為181.172 5 mm4。

將以上參數帶入式(4)可求得骨架層的等效厚度teq為6.219 1 mm。圓環半徑取中徑[9]，即有：

(5)

式中：R1為非粘結柔性管最內層半徑,mm。

帶入式(5)求得R為52.409 5 mm，骨架層材料為316L不銹鋼，彈性模量E為206 GPa。將彈性模量E、等效厚度teq及半徑R帶入式(3)求得單位長度下平面應力臨界壓潰值為79.06 MPa。

2 有限元模型分析

2.1 模型驗證

根據現有文獻，骨架層的螺旋纏繞角度對均勻外壓下臨界壓潰值影響較小，因此在研究中可以忽略不計。對骨架層承載能力影響較大的因素有材料非線性、初始橢圓度以及骨架層相鄰節之間的接觸方式[7]。其中材料非線性指的是材料的彈塑特性，即當應力超過材料的屈服極限時，應力與應變之間呈現一種非線性的增長關系，該因素對骨架層承載能力影響最大；骨架層在制造及安裝過程中，難免會有夾持等情況出現，從而導致其形狀改變，通常會呈現一種橢圓形狀。規定以橢圓的長徑與短徑之差和兩者之和的比值作為衡量其發生橢圓變形的標準，稱之為橢圓度。橢圓度越大，骨架層的承載能力越小。骨架層相鄰節之間的接觸方式對承載能力有所影響，例如綁定接觸或摩擦接觸以及摩擦接觸的摩擦因數等，同樣會影響骨架層的承載能力。本文所研究骨架層材料為316L不銹鋼，在0.2%初始橢圓度、相鄰節之間為摩擦接觸、摩擦因數為0.15的情況下分析其承載能力。

首先建立管道整體模型，如圖2a所示。在不考慮材料非線性、初始橢圓度及節間接觸的情況下，對其進行特征值屈曲分析，查看管道的壓潰形式，同時分析壓潰的臨界載荷值，與理論值進行對比，驗證理論模型的準確性。該分析中，骨架層的各節之間為綁定接觸，在管道軸向兩端限制軸向位移約束，同時打開弱彈簧開關，骨架層外表面施加1 MPa的均勻載荷。骨架層及特征值屈曲分析結果如圖2b所示。

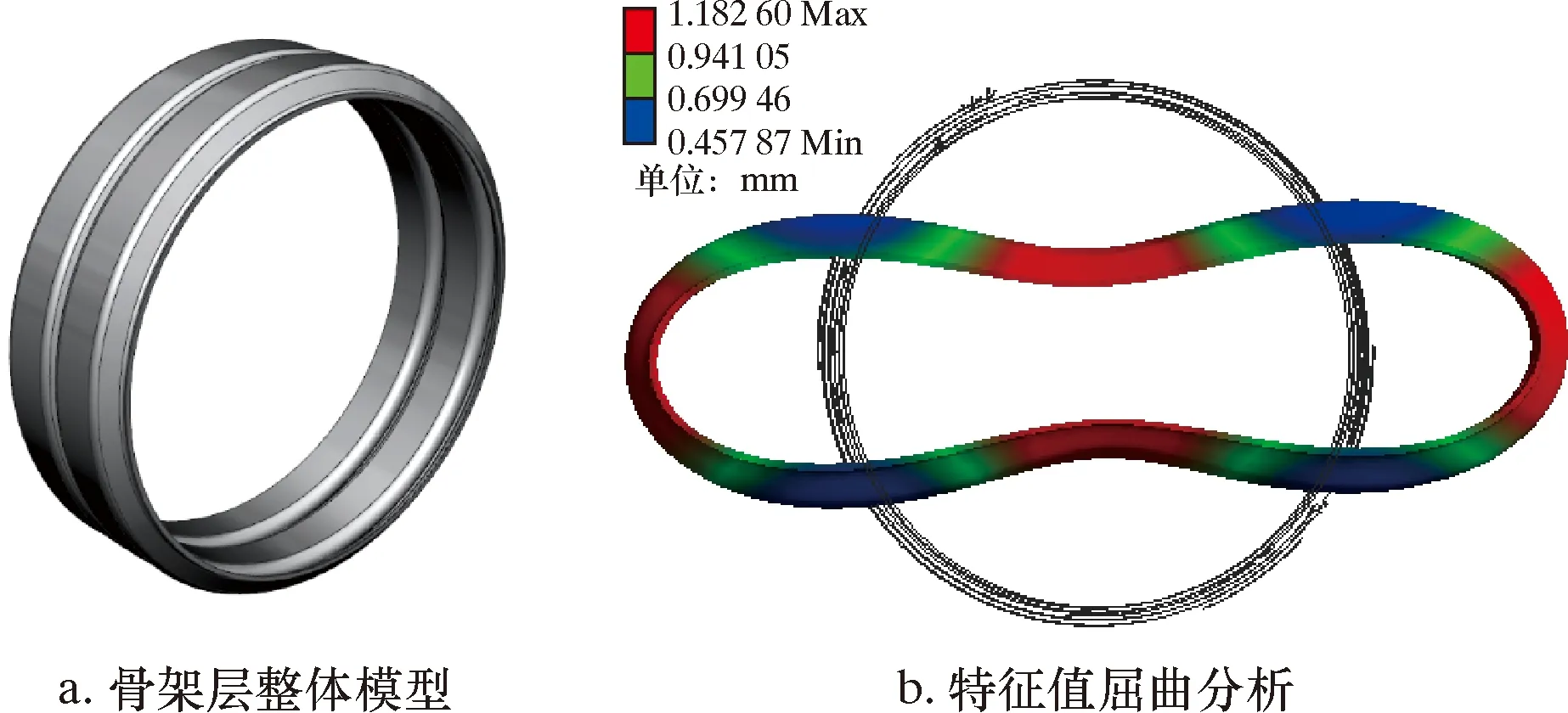
圖2 骨架層整體有限元分析

由圖2b可知，屈曲載荷系數為76.672，屈曲載荷等于屈曲載荷系數乘以施加載荷，由于施加的是單位載荷，所以屈曲載荷為76.672 MPa，即骨架層在該設定條件下的失穩值為76.672 MPa，與理論值對比如表1所示。

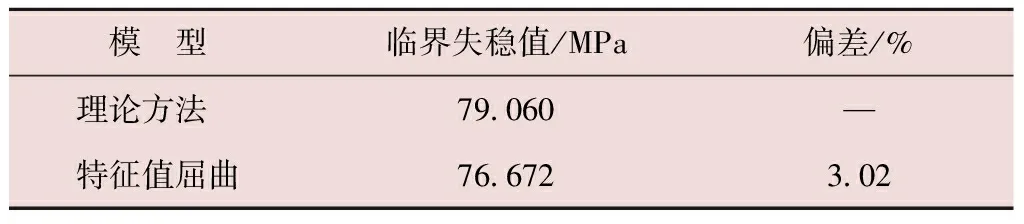
表1 特征值屈曲分析結果對比

由表1可知，骨架層特征值屈曲分析值與理論計算值很接近，驗證了用理論模型來計算無節間摩擦、完美圓狀態下彈性材料管道臨界失穩值的準確性。

2.2 數值模擬分析

在工作實際中，上述理想條件比較少，僅靠理論模型不能滿足要求，可借助數值模擬來進行分析。結合實際及現有理論，材料彈塑性對骨架層的承載能力影響很大，對于塑性材料，當應力超過比例極限后同樣采用上述分析顯然不合理。對于塑性分析有塑性極限載荷和塑性失穩載荷2個參量來衡量含缺陷管道的承載能力。當考慮材料應變硬化特性，載荷增加則變形增加，結構發生無限制塑性變形時的載荷就稱之為塑性失穩載荷；而假設材料為理想彈塑性材料時，管道所能承受的最大載荷稱之為塑性極限載荷，可用ASME規范中的2倍斜率準則來確定。

截止到目前，對于存在腐蝕缺陷的柔性管道承壓能力研究很少。本文研究了不同軸向、周向腐蝕長度及小范圍的徑向腐蝕深度對柔性管道骨架層承壓能力的影響。由于骨架層幾何尺寸及所受載荷的對稱性，為簡化模型，節省分析時間，只建立模型進行后續分析。

骨架層材料為316L不銹鋼，在20 ℃溫度下，屈服強度為210 MPa，抗拉強度為490 MPa，彈性模量E為206 GPa，泊松比為0.3，密度為7.98 g/cm3，伸長率為40%。

在材料參數設置時，選用雙線性隨動強化模型，切線模量可通過下式進行簡化計算。

(6)

式中：Tm為切線模量，MPa；Rm為抗拉強度，MPa；Ys為屈服強度，MPa；l為伸長率，無量綱。將以上參數帶入求得切線模量為700 MPa。

本文采用ANSYS Workbench軟件對非粘結柔性管道的骨架層進行有限元分析，依據所研究的橢圓度要求建立有限元模型。由于骨架層截面的不規則性，采用掃掠的方式進行網格劃分，以骨架層的2個對稱截面分別為源面和目標面，首先對源面進行網格劃分，然后沿圓周向目標面掃掠，完成實體的網格劃分，劃分結果如圖3a所示。模型節與節之間接觸面設置為摩擦接觸，摩擦因數為0.15[15]；在模型上下兩截面施加對稱約束，限制其法向位移，兩側邊界施加軸向的位移約束，限制其軸向位移，外表面施加均勻壓力載荷，如圖3b所示。

圖3 骨架層有限元模型

塑性極限載荷又稱之為垮塌載荷，本文以此為參量來衡量骨架層的承載能力，以無腐蝕缺陷的骨架層分析為例，外表面施加50 MPa均勻荷載，載荷步設置為1，步長為1 000 s，激活自動時間步，時間步類型選擇子步，初始載荷步、最小、最大載荷步分別為500、500和1 000。總載荷隨載荷子步分步施加，在其逐步施加總變形發生突變，取該突變點位移及應力云圖如圖4所示。經估算該點施加載荷約為15.95 MPa，明顯低于特征值屈曲分析時的臨界壓潰值，表明對于塑性材料，材料非線性是分析其承載能力必不可少的考慮因素之一，同時也說明在塑性材料的比例極限之前沒有失穩情況發生。

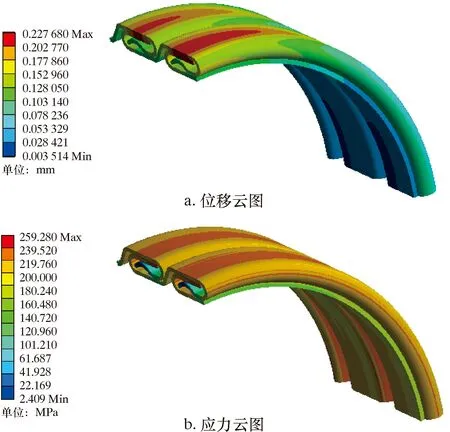
圖4 無腐蝕缺陷的骨架層仿真云圖

通過建立及改變骨架層內表面不同尺寸的矩形凹陷，來模擬實際情況中管道不同的腐蝕缺陷，研究不同缺陷尺寸對管道失效壓力的影響，矩形缺陷形貌如圖5所示。紅色區域為腐蝕坑，XC為軸向長度方向，ZC為周向長度切線方向，YC為徑向深度方向。

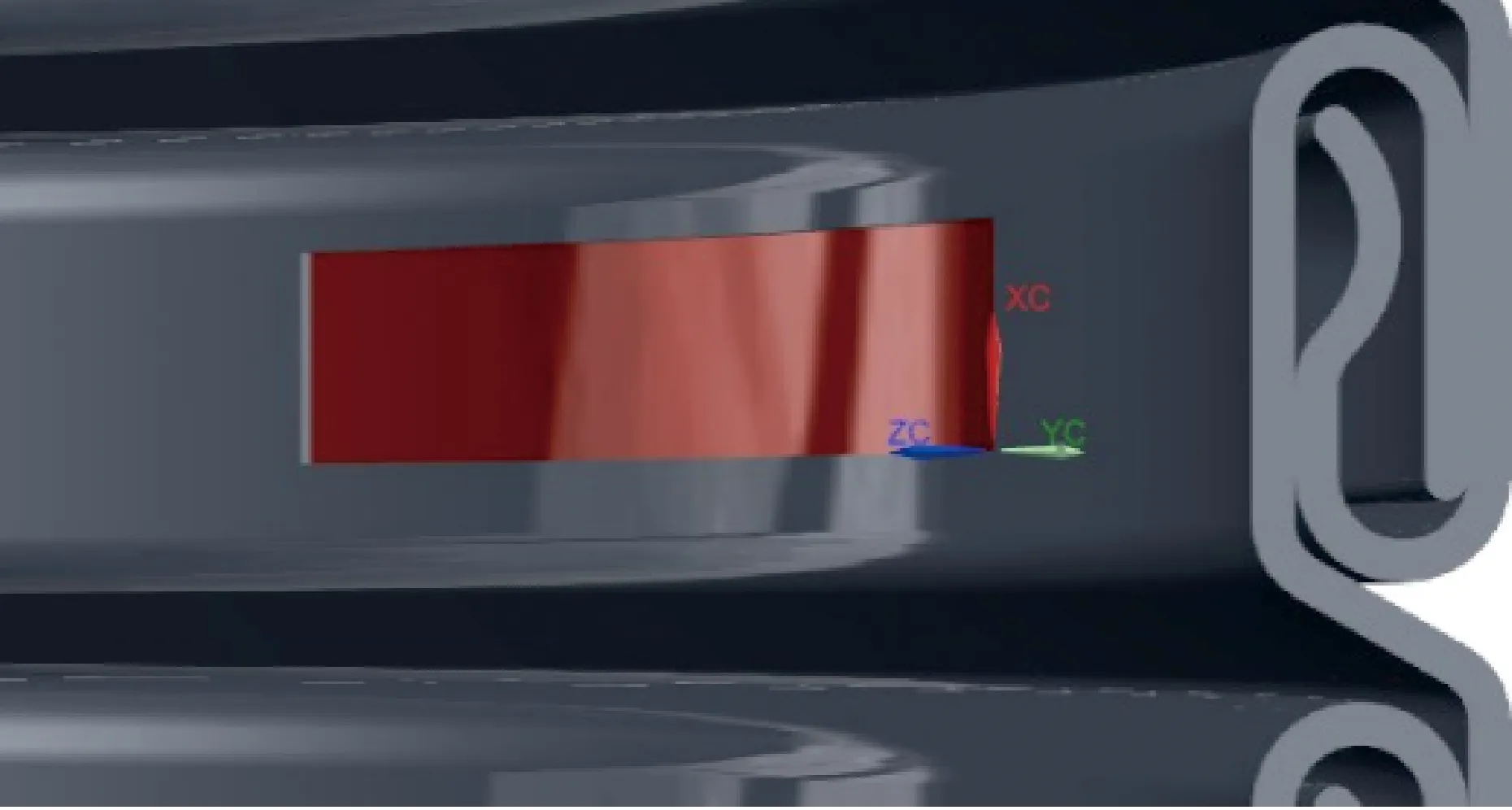
圖5 骨架層局部腐蝕缺陷示意圖

所建立矩形腐蝕缺陷尺寸如下：

當軸向長度為3 mm、徑向深度為0.5 mm時，缺陷周向長度為17.732 5、35.465 1及53.197 6 mm；當周向長度為35.465 1 mm、徑向深度為0.5 mm時，缺陷軸向長度為3、5和7 mm；當周向長度為35.465 1 mm、軸向長度為3 mm時，缺陷徑向深度為0.3、0.5和0.7 mm。

采用與無腐蝕缺陷模型同樣的步驟進行分析，根據分析結果，依據2倍彈性斜率準則[16]來確定骨架層的塑性極限載荷。在載荷-位移曲線中，斜率為彈性部分直線斜率2倍的直線與曲線的交點即為塑性極限載荷。采用該準則進行計算，結果如圖6所示。

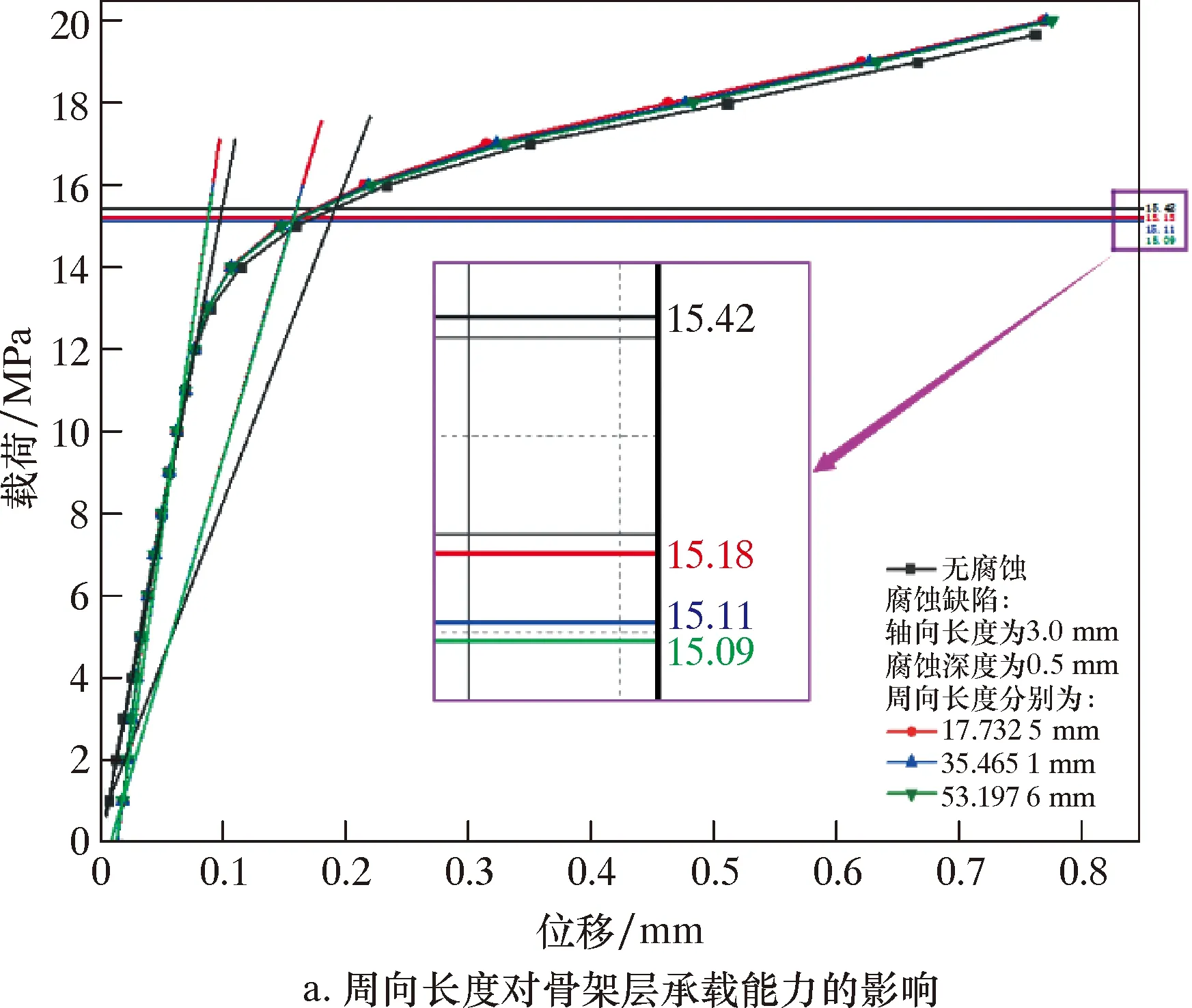
圖6 局部腐蝕塑性極限載荷的確定

將圖6依據2倍彈性斜率準則計算所得數據統計，結果如表2所示。

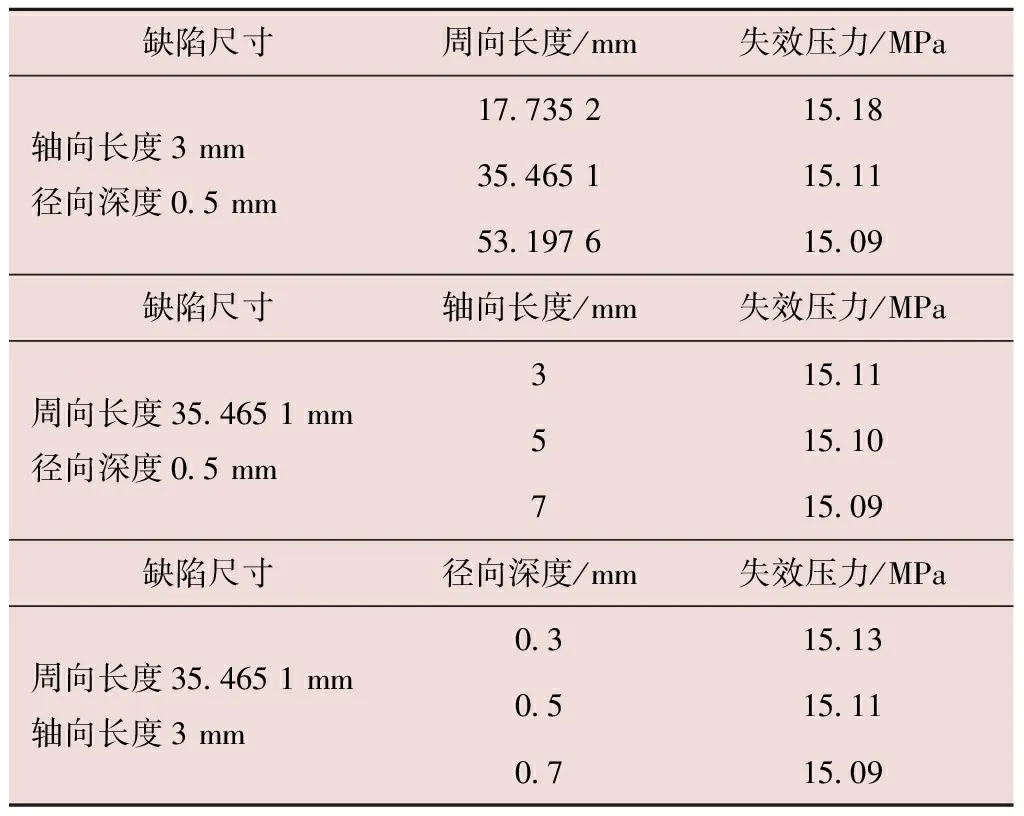
表2 管道失效壓力隨腐蝕缺陷尺寸變化情況

由上述分析可知，不同軸向、周向長度及徑向深度的腐蝕缺陷都能影響管道骨架層的失效壓力，但是影響甚微，可以忽略不計，即小范圍的局部腐蝕對骨架層承載能力的影響不大。由于骨架層與運輸介質直接接觸，考慮其內層緩慢的大面積均勻腐蝕對骨架層失效壓力的影響，因為骨架層內表面與所運輸的油氣水混合介質充分接觸，所假設的均勻腐蝕邊界如圖7所示。

圖7 骨架層均勻腐蝕的腐蝕邊界

分別以均勻腐蝕深度δ為0.1、0.2、……、0.8 mm的管道骨架層進行承載能力分析，同樣運用2倍彈性斜率準則來確定管道的塑性極限載荷，計算結果如圖8所示。

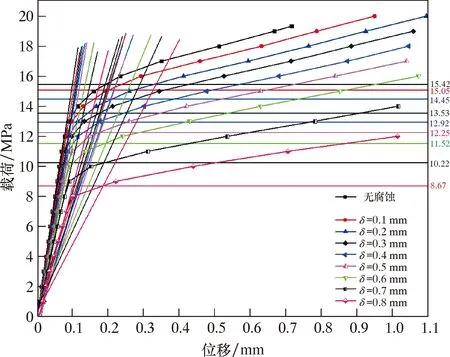
圖8 均勻腐蝕塑性極限載荷的確定

將圖8計算結果整理，結果如表3所示，其中Δp1為相鄰兩均勻腐蝕深度之間所對應的失效壓力差值。

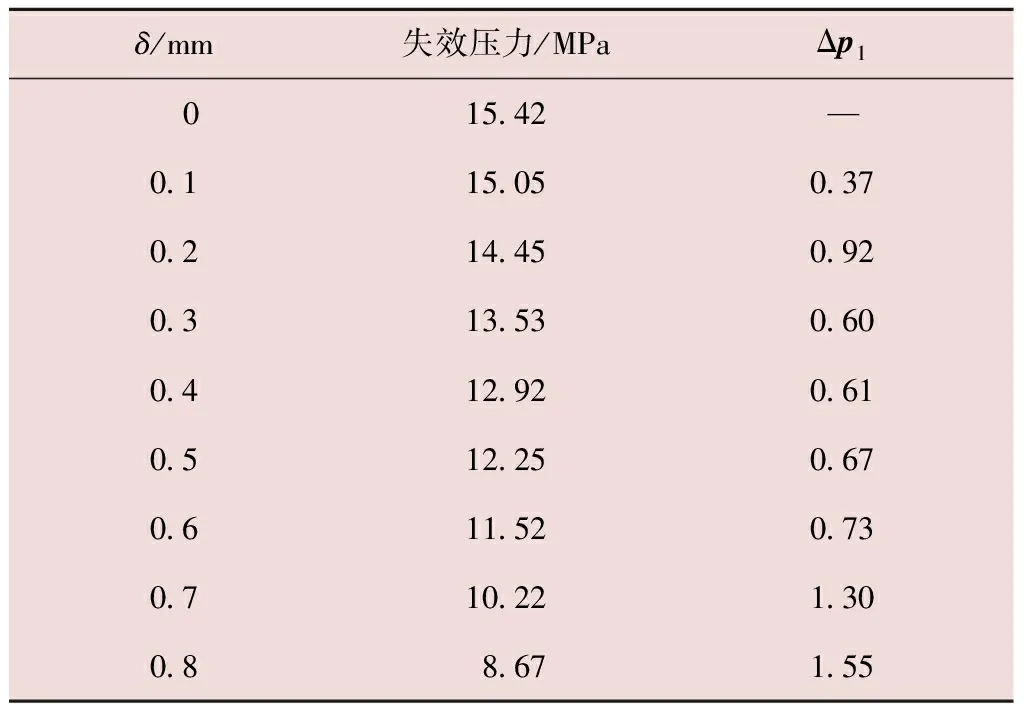
表3 管道失效壓力隨均勻腐蝕深度變化情況

由表3及圖8可知，隨著腐蝕深度的增加，骨架層失效壓力下降速度整體上逐漸增加，呈現為拋物線趨勢，對其進行非線性的擬合，如圖9所示。擬合公式為：

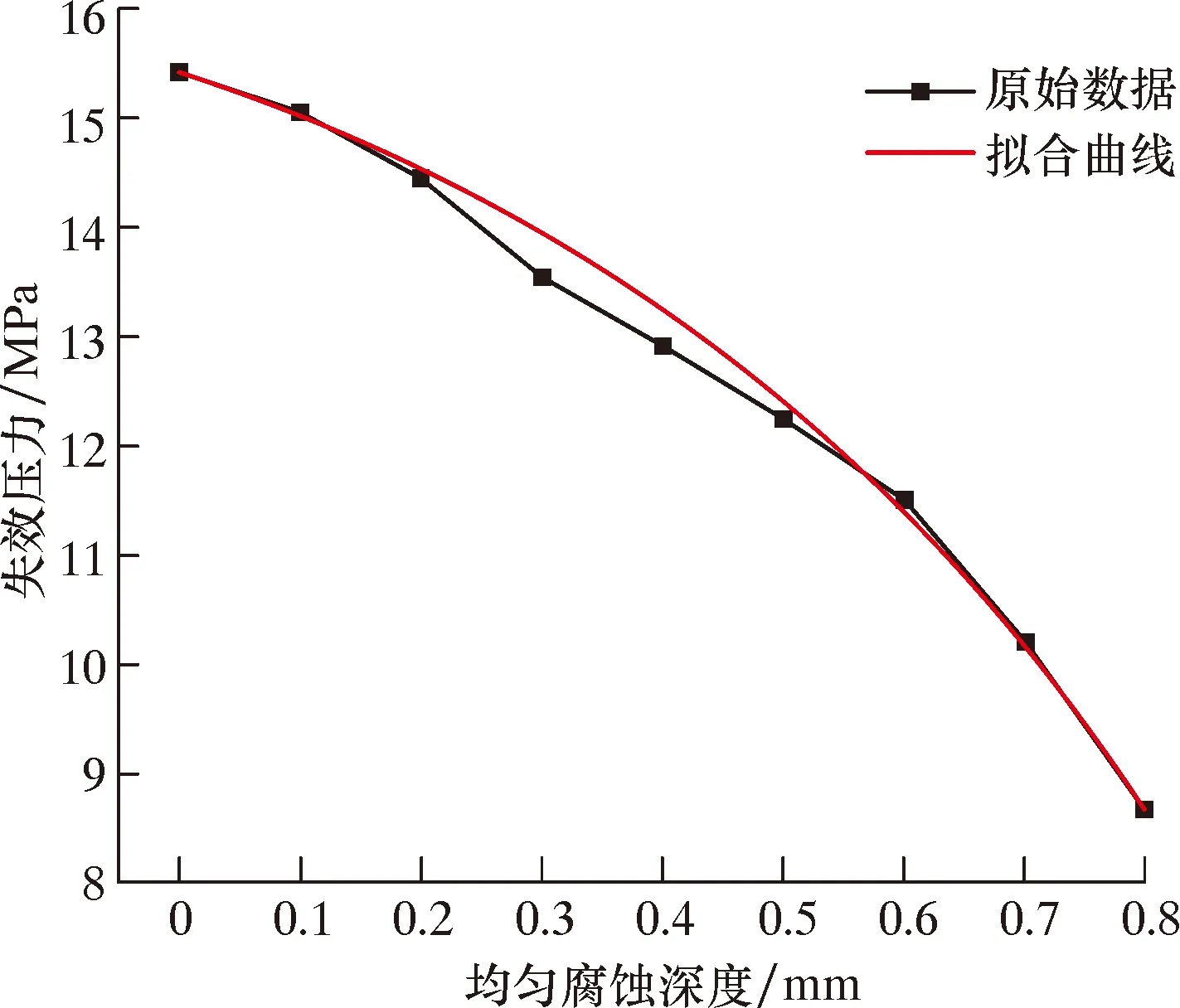
圖9 管道失效壓力隨均勻腐蝕深度變化情況

(7)

式中：y為骨架層失效壓力,x為均勻腐蝕深度。

擬合數據及誤差如表4所示，經檢驗，該模型決定系數為0.98，平均絕對誤差為0.139 8，均方誤差為0.041 4，誤差較小，擬合數據符合良好。

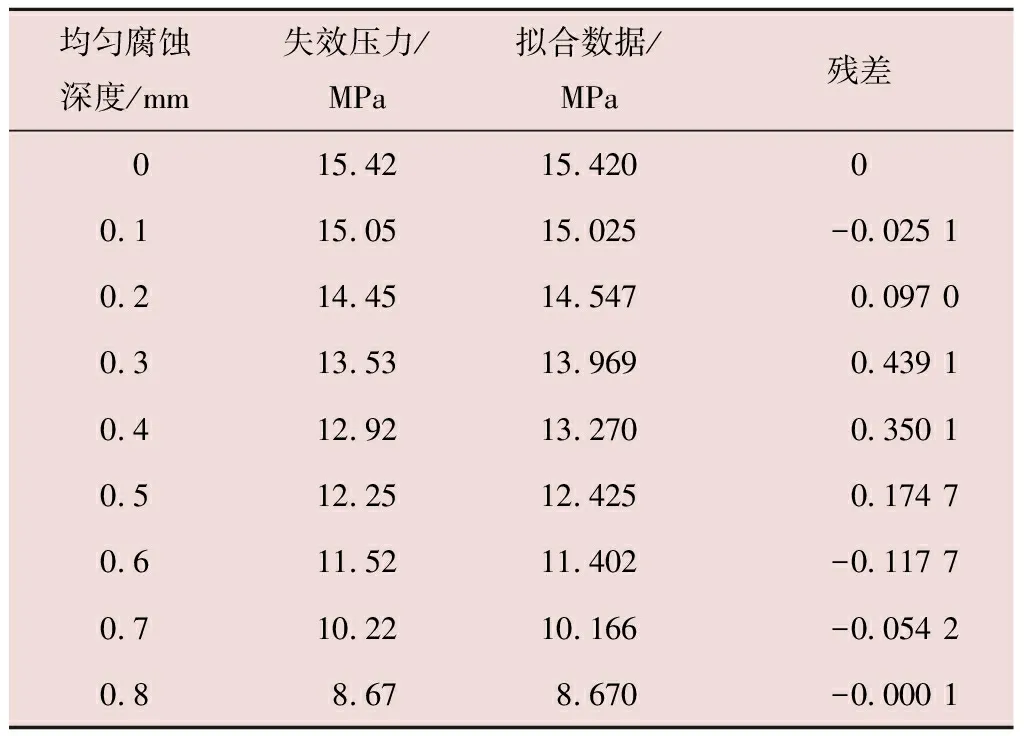
表4 擬合數據誤差檢驗

3 腐蝕預測模型建立

海底管道下一時刻的腐蝕狀態只與當前時刻有關。馬爾可夫性質如下[17-18]：一個隨機過程在給定現在及過去所有狀態情況下，其下一時刻所處狀態的條件概率分布僅取決于當前狀態。這與管道的腐蝕狀態轉移性質相符合，因此可借用離散的馬爾可夫過程，即馬爾可夫鏈模型來對管道的腐蝕狀態進行預測。馬氏鏈表示如下：

(8)

建立馬爾可夫預測模型的關鍵在于構建狀態轉移矩陣：

P=[Pij]n×n

(9)

Pij表示系統在t時刻處于狀態i，下一時刻(t+l)處于狀態j的概率；n為系統所有可能的狀態個數。預測模型的建立流程如圖10所示。

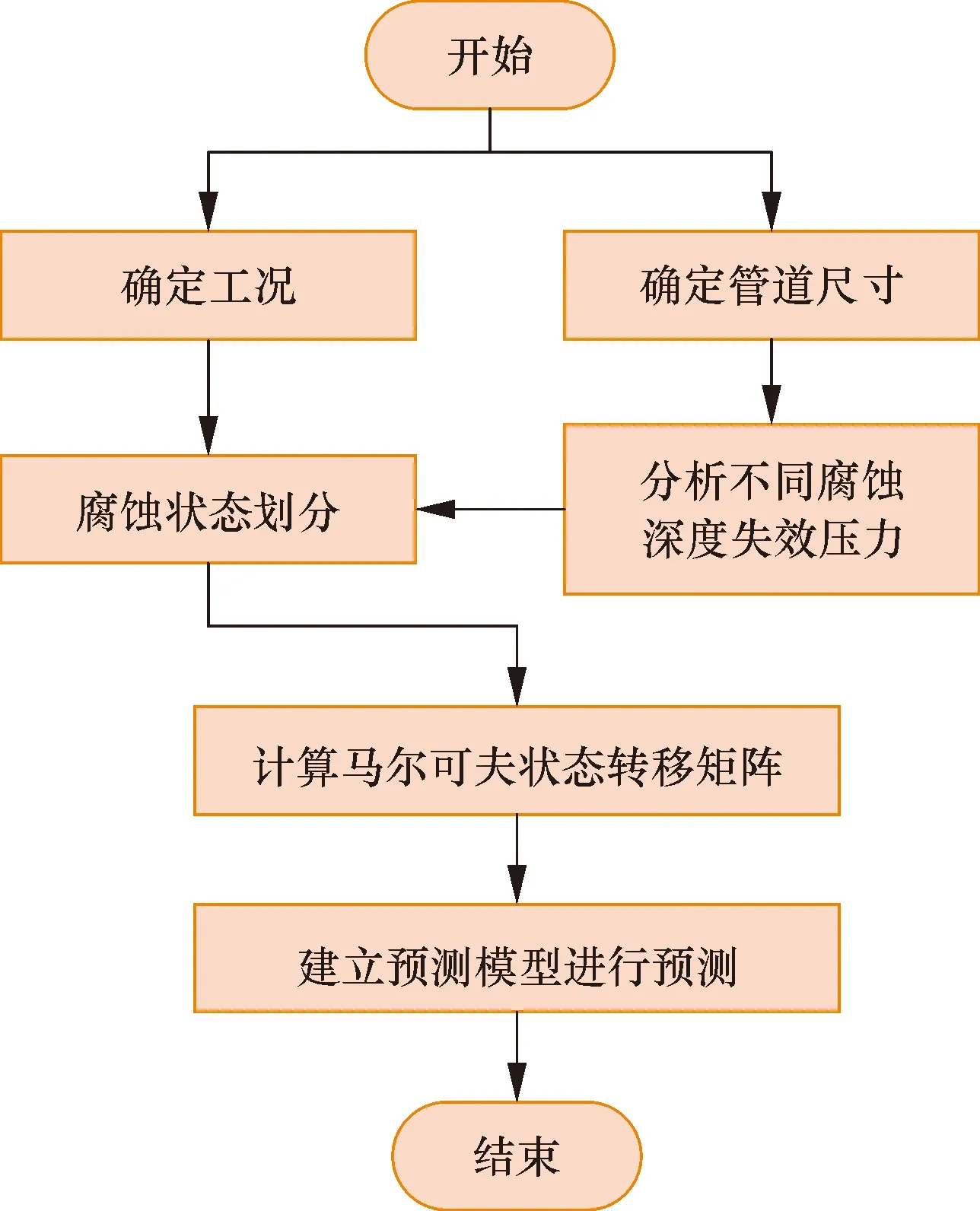
圖10 腐蝕預測模型構建流程圖

對于傳統剛性管道，根據SY/T 6151—2009《鋼制管道管體腐蝕損傷評價方法》，以管道的最大腐蝕深度為指標，將不同腐蝕程度的管道劃分為“輕、中、重、嚴重及穿孔”5個等級[19]，依次對應5種狀態，計算各狀態之間的轉移概率，可構建馬爾可夫狀態轉移矩陣，實現對管道所處腐蝕狀態的預測。而對于非粘結柔性管道骨架層復雜的幾何形狀，上述狀態劃分方式明顯不適用。依據不同腐蝕深度的骨架層承載能力分析，結合管道所處工況，可進行管道腐蝕狀態的劃分。以某管道2020—2021年工況為例，該管道輸送油氣水3項物質，其中輸氣量(標準狀態)為77×104m3/d，輸油量、輸水量都為4.62 m3/d，內壓范圍為3.10～4.27 MPa，外壓范圍為12～15 MPa，出、入口溫度分別為25.0和39.2 ℃。

管道不同管段的骨架層承受不同的內壓與外壓，當某管段內壓最小、外壓最大時，骨架層承受最大的壓力載荷，為11.30 MPa；當某管段內壓最大、外壓最小時，骨架層承受最小的壓力載荷，為7.73 MPa，因此該管道可能承受的壓力載荷范圍為7.73～11.3 MPa。根據式(7)計算可得，該失效壓力區間所對應的骨架層均勻腐蝕深度為0.609～0.854 mm，即當均勻腐蝕深度小于0.5 mm時，管道處于安全狀態，定義腐蝕狀態為輕度腐蝕；當腐蝕深度處于0.5～0.6 mm之間時，雖然管道失效壓力大于工況所施加的載荷，但該階段的失效壓力隨腐蝕深度變化較快，有即將失效的風險，定義腐蝕狀態為中度腐蝕；當均勻腐蝕深度處于0.60～0.85 mm之間時，管道中某些位置骨架層失效壓力小于工況所施加的壓力載荷，故定義腐蝕狀態為重度腐蝕；當繼續腐蝕，腐蝕深度大于0.85 mm時，管道骨架層失效壓力小于工況所施加的最小載荷，管道完全失效，定義該階段腐蝕狀態為失效。即該工況腐蝕狀態劃分如下：①輕度腐蝕，均勻腐蝕深度小于0.5 mm；②中度腐蝕，均勻腐蝕深度在0.5～0.6 mm之間；③重度腐蝕，均勻腐蝕深度在0.60～0.85 mm之間；④失效，均勻腐蝕深度大于0.85 mm。

腐蝕過程中，若不采取措施，劣化狀態會越發嚴重，隨著時間的延長，或停留在當前狀態，或越來越差，因此狀態④，即失效狀態只能停留至該狀態，不能向其他狀態轉移，其值為1。根據上述劃分的4種腐蝕狀態，可得馬爾可夫狀態轉移矩陣如下：

(10)

式(10)中，Pij(i，j=1，2，3，4)為狀態轉移概率，表示當前時刻為i狀態，下一時刻為j狀態的概率。已知初始狀態為T(0)=[a，b，c，d]，其中，a、b、c、d分別為初始時刻管道處于各狀態的概率，則n年后管道所處腐蝕狀態為T(m)=T(0)×P(n)。至此，完成管道所處腐蝕狀態的預測。

4 結 論

基于ANSYS Workbench軟件對非粘結柔性管道骨架層進行了特征值屈曲分析，并與理論值作對比。另外，在不考慮螺旋纏繞角度、初始橢圓度為0.2%、考慮材料彈塑性及節間摩擦接觸條件下，對腐蝕缺陷形貌及尺寸對骨架層承載能力的影響規律進行了分析，并借助分析結果構建了馬爾可夫預測模型，得出如下主要結論：

(1)結合鐵木辛柯彈性穩定理論中的圓環撓曲線微分方程，根據單位長度彎曲剛度相等將骨架層等效成截面為矩形的圓環，計算其臨界失穩值；建立骨架層有限元模型并對其進行特征值屈曲分析，將分析結果與理論計算結果進行對比，誤差為3.02%，驗證了理論模型對于無節間摩擦、完美圓狀態下彈性材料管道的承載能力計算的可行性。

(2)對于塑性材料，采用理論模型或特征值屈曲方式來進行分析顯然不合理，本文以塑性極限載荷為參量來衡量骨架層的承載能力。通過分析矩形腐蝕缺陷的周向、軸向長度及徑向深度對骨架層承載能力的影響，發現小范圍的局部腐蝕缺陷對其影響不是很大，可以忽略，考慮到骨架層內層與運輸介質直接接觸，分析了骨架層內層均勻腐蝕對承載能力的影響，分析結果顯示該種腐蝕影響較大。

(3)分析均勻腐蝕深度對管道失效壓力的影響規律發現，失效壓力曲線呈拋物線形式，對其進行非線性擬合，得到均勻腐蝕深度與骨架層失效壓力的關系式，經檢驗，該關系式計算所得結果與仿真結果吻合較好。

(4)在管道腐蝕狀態預測時，由于現有的腐蝕狀態劃分方式對非粘結柔性管骨架層的不適用性，基于分析結果，建立了針對柔性管的腐蝕狀態劃分新方式，并且建立了馬爾可夫預測模型進行預測。