基于最小二乘法橢圓擬合的改進型快速算法*

朱森榮 劉杰徽

（1.海軍工程大學兵器工程學院 武漢 430033）（2.重慶前衛科技集團有限公司技術中心 重慶 401121）

1 引言

橢圓擬合在圖像識別、特征提取中有著特別重要的意義。而最小二乘法是數據擬合的最常用方法，受隨機噪聲的影響整體最小[1]，是電子羅盤校準算法中應用最常用的算法之一，廣泛應用于航空、航天、航海、水中兵器、石油鉆井等領域[2]。

在實際應用過程中往往通過大量的數據進行擬合，計算量偏大，而單片機的算力每秒只有幾萬次浮點運算能力，而橢圓擬合需要快速而且大量的浮點運算資源，如果需要在單片機上進行曲線擬合的話就會大大影響系統的性能，因而需要進一步研究快速算法，在計算資源嚴重缺乏的單片機上算法的簡化顯得尤為重要[3]。

本文給予最小二乘法進行了一些簡單的改進，引入樣本點分組原理，再對樣本點進行隨機抽取，并且通過Matlab仿真驗證可以一定程度上減少算法的復雜度，提升算法的實時性。

2 最小二乘橢圓擬合方法介紹

橢圓的代數表達式如下：

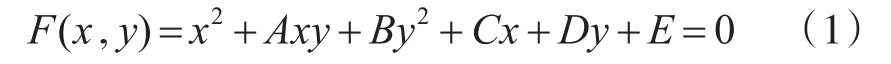
表達式中有5個未知數，分別為A、B、C、D、E。

最小二乘法是由最大似然法推出的一個最優估計技術，它可使測量誤差的平方和最小，也就是所有離散點到曲線的代數誤差之和最小[4]，因此也被視為從一組測量值中求出一組未知量的最可信賴的方法之一[5]。

平面內某點（x0，y0）到方程（fx，y）=0所代表曲線的代數距離就是f(x0，y0)，對離散樣本點進行最小二乘處理，即目標函數如下

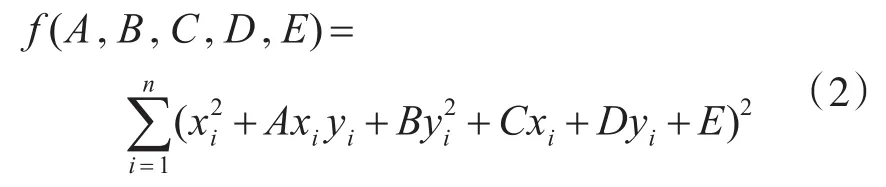
根據橢圓的幾何知識，可以計算出橢圓的五個參數：位置參數（θ，x0，y0）和形狀參數（a，b）。……