時態圖最短路徑查詢方法

張天明 徐一恒 蔡鑫偉 范 菁

1(浙江工業大學計算機科學與技術學院 杭州 310023) 2(浙江大學計算機科學與技術學院 杭州 310013)

圖，作為一種通用的數據結構，用于表示各種對象之間的復雜關聯關系.圖上最短路徑計算作為基礎功能函數，有著廣泛的應用.例如，路徑規劃、城市交通路線優化、社交網絡分析等.現有的最短路徑算法主要聚焦在普通圖，然而，真實場景中，圖中常常附有時態信息，2個頂點之間的邊關聯的事件在某一時間點發生并持續一段時間結束，此種類型的圖稱之為時態圖.

Fig. 1 Illustration of bus timetable圖1 公交時刻圖示例

圖1列舉了時態圖應用在公交時刻圖的例子.圖中頂點表示公交站點，時態邊上附帶有時態區間，表示公交車從一個站點到另一個站點的出發時間和到達時間.例如，一班89路公交車早上7∶00從浙大玉泉校區始發站出發，7∶15到達古蕩站點，停靠站1 min，7∶16出發，經府苑新村，蔣村公交站，最終在8∶15到達三墩終點站.此例中，時態圖最短路徑查詢有助于乘客查詢指定時態區間內的2個站點間的最短路徑，從而為乘客智能推薦公交線路.給定時態圖

G

=(

V

,

E

)，查詢源點

u

，查詢目的點

v

，時態區間

I

，本文研究的時態圖最短路徑旨在圖

G

中查詢

u

到

v

在時態區間

I

內的最短時態路徑距離

.

時態圖

G

中的邊除了關聯時態區間外，還附加有權重值，在交通路網中可以表示距離；在公交

/

地鐵

/

航班時刻圖中可以表示費用；在社交網絡中可以表示用戶之間的親密度

.

與已有的最短路徑查詢問題相比，最短時態路徑更具挑戰性

.

首先，計算最短時態路徑時需要考慮邊與邊的時序流轉特性，否則如果運用現有的普通圖最短路徑計算方法，會產生錯誤的結果.例如，圖1中，假設邊上權值均為1，乘客想要查詢云棲小鎮站到三墩站在時態區間[7∶00,9∶00]的時態最短路徑距離.如果不考慮邊之間的時序流轉特性，則計算得到的結果為3，對應的最短時態路徑為(云棲小鎮，府苑新村，蔣村公交站，三墩)或(云棲小鎮，府苑新村，董家村，三墩).實際這2條路徑均不能到達三墩站.對于第一條路徑，121路云棲小鎮到府苑新村時間為8∶20，其不能趕上7∶32從府苑新村出發經由蔣村公交站最終到達三墩站的89路公交車.對于第二條路徑，121路換乘70路8∶50到董家村，同樣趕不上8∶26到三墩站的12專線.鑒于此，時態最短路徑計算過程中需要考慮時序流轉特性，此例計算得到的結果應為4，對應的最短時態路徑應為(云棲小鎮，翠苑，大關，董家村，三墩).

其次，最短時態路徑并不滿足子路徑最優性質,即頂點

u

到頂點

v

的最短時態路徑的子路徑并不一定是最短時態路徑.上例中，子路徑(云棲小鎮，翠苑，大關，董家村)并不是時態區間[7∶00,9∶00]內的最短時態路徑，云棲小鎮到董家村在時態區間[7∶00,9∶00]內最短時態路徑應為(云棲小鎮，府苑新村，董家村).這導致計算時態最短路徑時更復雜，因為需要考慮所有的路徑.

目前，已有一些工作研究時態圖最短路徑查詢.然而，它們一般假設輸入時態圖為FIFO(first-in-first-out)時間依賴圖，FIFO時間依賴圖是指圖輸入邊上的時間間隔表示為出發時間的函數，這個函數具有FIFO屬性，即若出發時間早，則到達時間也早.這類問題具有一定的特殊性，實際交通工具出行時刻圖或社交接觸網絡不一定是FIFO時間依賴圖.與本文工作最相關的是文獻[6-7]提出的one-pass算法，其將時態圖轉化為普通圖，而后在普通圖上采用廣度優先搜索和Dijkstra算法計算最短時態路徑，但其在較大規模數據集上效率較低.鑒于此，本文研究時態圖最短路徑問題并提出了基于層次索引的計算方法，其主要包含預處理和在線查詢2個階段.預處理階段本文提出了一種無損壓縮方法和層次索引CTG-tree(compressed transformed graph tree).首先將時態圖轉化為普通圖，對普通圖進行壓縮以減小規模，將時態圖上最短路徑計算轉化為在壓縮結果圖上執行.而后在壓縮結果圖上構建CTG-tree，它將G-tree的思想擴展到壓縮有向圖上，首先采用Metis劃分將壓縮圖層次劃分為若干個子圖，得到每個子圖的入邊界點與出邊界點集合.CTG-tree為每個葉子節點對應子圖計算其內部頂點與出邊界點的最短路徑、入邊界點到子圖內頂點的最短路徑和出邊界點到入邊界點的最短路徑；非葉節點計算其對應子圖入邊界點到其所有孩子節點對應子圖的入邊界點之間的最短路徑距離、所有孩子節點對應子圖的出邊界點到當前非葉節點對應子圖的出邊界點之間的最短路徑距離、以及所有孩子節點對應子圖的出邊界點到所有孩子節點對應子圖的入邊界點之間的最短路徑距離作為索引.查詢階段本文基于層次索引CTG-tree設計了高效的最短路徑查詢算法.概括而言，本文的主要貢獻有4個方面:

1) 提出了一種基于層次索引的兩階段(預處理階段和查詢階段)方法以高效地計算時態圖最短路徑;

2) 提出了一種無損壓縮方法和層次索引CTG-tree，將時態圖上最短路徑計算結果轉化為在壓縮結果圖上執行.CTG-tree將G-tree的思想擴展到壓縮有向圖上；無損壓縮在減小圖處理規模的同時還保證了壓縮結果圖上最短路徑計算的準確性；

3) 提出了基于CTG-tree索引的查詢算法以高效地支持時態圖最短路徑查詢;

4) 基于4個真實的時態圖數據集，進行了充分的實驗評估，驗證了本文提出的基于層次索引的最短時態路徑算法的高效性.

1 相關工作

本節分別概述已有的普通圖和時態圖最短路徑查詢算法.

1.1 普通圖最短路徑查詢算法

綜述文獻[1,9]將普通圖最短路徑問題劃分為點到點的最短路徑計算、單源最短路徑計算和所有點對最短路徑計算3類問題.點到點的最短路徑計算指定點對之間的最短路徑；單源最短路徑計算一個點到其他所有點的最短路徑距離；所有點對最短路徑計算圖中所有點對之間的最短路徑距離,其可通過單源最短路徑計算得到.已有的最短路徑查詢算法大多是基于經典的Dijkstra方法，文獻[10]從理論角度分析了單源最短路徑基于堆的優先級隊列算法的時間復雜度是

O

(

m

log

n

)；采用斐波那契堆的時間復雜度是

O

(

m

+

n

log

n

).文獻[11]提出了基于Dijkstra的變體方法Sky-Dijk.為了縮小搜索空間，雙向搜索算法被提出.由于Dijkstra方法及其變體算法在大圖上運行時間較長，因此研究人員提出了一系列基于索引的最短路徑算法以提高查詢效率.例如，文獻[14]提出了基于標志點(landmark)的算法，其預先選擇一些頂點作為標志點；并且預先計算圖中每個頂點與標志點之間的最短路徑距離.圖中任意一對頂點之間的最短路徑距離上下界可以運用預先計算好的距離計算得到；文獻[15]提出了基于剪枝的標志點標簽，通過剪枝的廣度優先搜索預計算所有頂點的距離標簽，通過距離標簽計算任意點對的最短路徑距離.文獻[16]提出了收縮層級結構；將圖中的頂點或者邊按照重要度排序，再根據排序的結果迭代，最終生成層級嵌套索引.文獻[8]提出了G-tree索引，其首先將路網層次劃分為若干個子圖，再計算每個子圖內的頂點與邊界點之間的距離，子圖間的邊界點與邊界點之間的距離作為索引，基于G-tree索引提高查詢效率.基于索引的最短路徑算法關鍵在于平衡查詢時間、索引時間、索引空間；為了減小索引空間，文獻[17-18]還提出了索引壓縮方法.針對動態圖，文獻[19]提出了DCHvcs,其擴展收縮層級結構以支持動態圖.文獻[20]在收縮層級最短路徑索引的基礎上，構建輔助的圖結構以及權重傳播機制來處理流式和批量的路網權重更新.文獻[21]提出了CRP方法以支持最短路徑索引的動態更新.針對大規模輸入圖，文獻[22]基于分布式流處理系統Yahoo S4，提出了2種異步通信算法以支持動態最短路徑；文獻[23]探索了邊受限的最短路徑查詢問題.此外，一些研究人員還致力于近似最短路徑計算方法研究.文獻[24]提出了距離Oracle數據結構，對于(2

k

-1)-近似能在

O

(

k

)的時間內給出任意節點對之間的近似最短路徑.文獻[25]將大圖近似為一個規模相對小的spanner稀疏子圖，而后在子圖上做近似最短路徑計算.概括而言，上述算法均針對普通圖，并沒有考慮邊上附帶的時態信息，因此不能直接有效地應用在時態圖上.

1.2 時態圖最短路徑查詢算法

綜述文獻[1]總結了時間依賴圖的最短路徑查詢算法.時間依賴圖中邊延遲函數計算一條邊中源點到目的點所需時間，時間函數可分為離散或連續的.

文獻[2,6-7,26]針對離散時間下的最短路徑進行了研究.文獻[2]提出了TD-G-tree索引以支持時間依賴路網上最短路徑查詢，但是其與本文研究問題不同，并沒有考慮路徑內邊之間的時序關系.文獻[26]提出了時間表標簽(time table labelling, TTL)索引；文獻[6-7,27]提出將時態圖轉化為普通圖，基于此，文獻[27]研究了時間依賴的可達性查詢，其提出了TopChain標簽索引方法以解決時態圖上的可達性查詢、最早到達時間查詢、最小間隔時間查詢.與其研究的問題不同，本文旨在解決時態圖上的最短路徑查詢.文獻[6-7]在轉化的普通圖上采用廣度優先搜索和Dijkstra算法計算2點之間給定時間段內的最短路徑.本文基于上述工作，將時態圖轉化為普通圖后，利用壓縮以及層次索引技術高效支持最短時態路徑查詢.

文獻[3-5]針對連續時間下的最短路徑進行了研究.文獻[4]提出了基于Dijkstra算法返回耗時最少旅行時間的最優出發時間；文獻[3]首先定位給定時態區間段內子圖，而后在子圖中采用Dijkstra計算最短路徑.文獻[5]在文獻[4]的基礎上，研究的時態圖中邊除了邊延遲函數外，還添加了權重代價函數，利用這2種函數的結構屬性設計最短路徑算法.這類工作通常假設輸入時態圖為FIFO時間依賴圖，輸入邊上時間間隔表示為出發時間的函數，出發時間早，則到達時間也早，這類問題具有一定的特殊性.而在我們的問題中，輸入邊有出發時間和到達時間，輸入圖(例如交通工具出行時刻圖或者社交接觸網絡)不一定是FIFO時間依賴圖，這導致計算時態最短路徑時更復雜，最短路徑計算不滿足最優子結構特征，因為需要考慮邊與邊的時序流轉特性，計算難度更高.

2 問題定義

本節主要介紹時態圖、時態路徑相關概念，最后給出問題定義.

定義1.

時態圖

.

本文定義的時態圖是復雜有向圖，表示為

G

=(

V

,

E

)，其中

V

表示頂點集合；

E

?

V

×

V

是有向邊的集合，具體地，連接頂點

u

∈

V

到

v

∈

V

/

{

u

}的有向邊

e

∈

E

表示為一個五元組(

u

,

v

,

w

,

s

,

a

)，表示

u

與

v

之間的事件發生起始時間是

s

，終止時間是

a

.

時間間隔是

I

=(

s

,

a

)，持續時間為|

I

|=

a

-

s

，

w

表示每條時態邊

e

的非負權重值，表示耗費時間或者路程等

.

不同于簡單圖，時態圖中2個頂點之間可能有多條時態邊

.

與普通圖路徑定義不同，時態圖中時態路徑的定義如下：

給定時態圖

G

，源點

s

，目的點

s

′，時間間隔

I

=[

t

,

t

]，定義函數

TPSet

(

s

,

s

′,

I

=[

t

,

t

])為從頂點

s

到頂點

s

′的所有滿足

S

≥

t

,

E

≤

t

的

G

中的時態路徑

p

構成的集合

.

基于此給出定義3

.

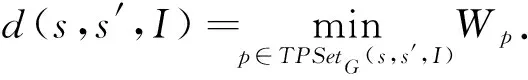
3 CTG-Tree構建

本文提出了基于層次索引的計算方法，主要包含預處理和在線查詢2個階段.本節詳細闡述預處理階段提出的無損壓縮方法和層次索引CTG-tree.

3.1 基于轉化圖的無損壓縮

在時態圖上計算最短時態路徑的直接方法是進行廣度優先搜索或者深度優先搜索，但是由于時態最短路徑不滿足子路徑最優性質，因此在搜索過程中需要保存計算遍歷到的所有路徑，此種方法效率較低.因此本文的主要思想是先將時態圖轉化為普通圖，而后進行壓縮，再利用索引加速查詢.具體地，本文利用文獻[6]提出的方法將時態圖

G

=(

V

,

E

)轉化為普通圖

G

=(

V

,

E

)，其中轉化圖

G

已被證明為有向無環圖，具體的轉化過程如下

.

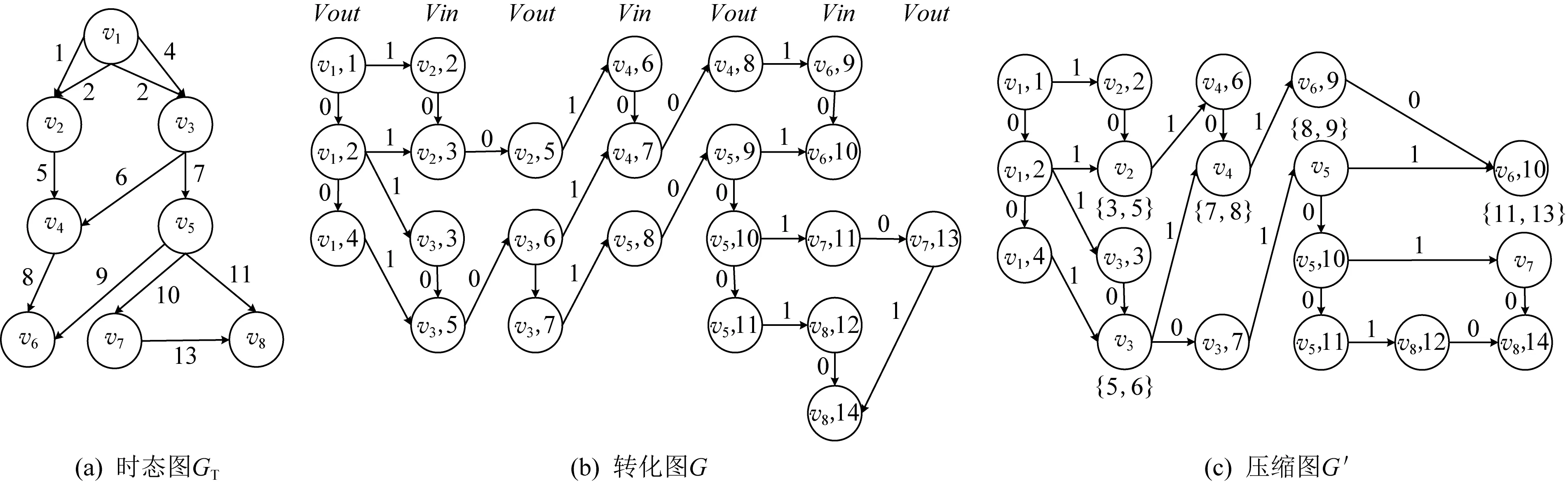
Fig. 2 Illustrations of temporal graph,transformed graph, and compressed graph圖2 時態圖、轉化圖和壓縮圖示例

算法1.

基于轉化圖的無損壓縮算法

.

輸入：基于時態圖

G

=(

V

,

E

)的轉化圖

G

=(

V

,

E

)；輸出：無損壓縮圖

G

′=(

V

′,

E

′)

.

/

*根據規則進行壓縮*

/

④ end if

⑤ end for

⑥ 輸出無損壓縮圖

G

′=(

V

′,

E

′)

.

3.2 CTG-tree索引

基于上述無損壓縮圖，構建層次索引CTG-tree.分為2個步驟：

1)
圖層次劃分.由于Metis劃分保證每次劃分的子圖頂點數目相近，交叉邊數目較少，因此本文采用Metis層次劃分，首先將無損壓縮圖

G

′劃分為若干子圖

G

，

G

，…，

G

(

l

≥2)，而后在每個子圖

G

(1≤

i

≤

l

)上進行迭代劃分直至劃分的子圖頂點數目不超過指定的閾值

θ

；最終形成平衡樹CTG-tree

.G

′為CTG-tree的根節點，第

i

次迭代劃分的子圖為CTG-tree第

i

層節點，葉子節點對應子圖的頂點數目不超過閾值

θ.

Metis劃分屬于邊劃分方法，每次迭代劃分的子圖之間沒有交集(例

G

∪

G

∪…∪

G

=

G

′,

G

∩

G

∩…∩

G

=?)，但是會產生跨子圖的交叉邊

e

(

u

,

v

),

u

∈

G

,

v

∈

G

.

基于此，本文將子圖內頂點分為3類：入邊界點、出邊界點和內部頂點

.

令

G

.B

,

G

.B

,

G

.V

分別表示子圖

G

=(

V

,

E

)的入邊界點、出邊界點和內部頂點的集合，則①

V

=

G

.B

∪

G

.B

∪

G

.V

；② ?

u

∈

G

.B

，至少存在一條跨分區的交叉邊

e

=(

u

,

m

),

u

與

m

隸屬不同子圖，即

m

?

G

；③ ?

v

∈

G

.B

，至少存在一條跨分區的交叉邊

e

=(

s

,

v

),

s

與

v

隸屬不同子圖，即

s

?

G

；④ ?

v

′∈

G

.V

，

v

′的所有入度鄰居

.

出度鄰居都隸屬子圖

G

，即

N

(

v

′)?

V

,

N

(

v

′)?

V

；在圖劃分步驟中，每個子圖記錄相應的入邊界點，出邊界點

.

2) 最短路徑距離矩陣計算

.

對于CTG-tree中的葉子節點對應的子圖

G

，需要計算3個最短路徑距離矩陣，即游出距離矩陣

G

.

、游入距離矩陣

G

.

和邊界點距離矩陣

G

.

.

G

.

保存

G

中所有頂點到每個出邊界點的最短路徑距離；

G

.

保存

G

中每個入邊界點到所有頂點的最短路徑距離；

G

.

保存

G

中所有出邊界點到入邊界點的最短路徑距離

.

對于CTG-tree中的非葉子節點對應的子圖

G

，需要計算出邊界點游入距離矩陣

G

.

、入邊界點游入距離矩陣

G

.

和邊界點游出距離矩陣

G

.

；

G

.

保存

G

所有孩子節點對應子圖的出邊界點到

G

所有孩子節點對應子圖的入邊界點之間的最短路徑距離；

G

.

保存

G

入邊界點到

G

所有孩子節點對應子圖的入邊界點之間的最短路徑距離；

G

.

保存

G

所有孩子節點對應子圖的出邊界點到

G

出邊界點之間的最短路徑距離

.

具體的CTG-tree索引構建算法偽碼如算法2所示

.

算法2.

CTG-tree索引構建算法

.

輸入：無損壓縮圖

G

′=(

V

′,

E

′)，Metis每層劃分的子圖數

l

，葉子子圖頂點數閾值

θ

；

輸出：CTG-tree索引.

① CTG-tree←

Metis

(

G

′,

l

,

θ

)；

② for each layer(自底向上) of CTG-tree

③ if leaf node←

/

*葉子節點層計算*

/

④

G

.

,

G

.

,

G

.

←

Dijkstra

(

G

′)；⑤ else

/

*非葉子節點層計算*

/

⑥

G

.

←

Dijkstra

(

G

′);

G

.

←

Dijkstra

(

G

′);

G

.

←

Dijkstra

(

G

′)；

⑦ end if

⑧ end for

⑨ 輸出CTG-tree索引.

算法2首先在給定的無損壓縮圖

G

′上進行Metis層次劃分，得到CTG-tree(行①)，需要說明的是，無損壓縮圖中，邊權重為0會影響Metis劃分過程，因此需要適當增權處理.接著，對CTG-tree自底向上遍歷計算索引矩陣(行②).對于葉子節點，利用Dijkstra算法在圖

G

′上計算葉子節點對應子圖

G

的游出距離矩陣

G

.

、游入距離矩陣

G

.

和邊界點距離矩陣

G

.

(行③～④)

.

對于非葉節點，利用Dijkstra算法在圖

G

′上計算對應子圖

G

的出邊界點游入距離矩陣

G

.

、邊界點游出距離矩陣

G

.

和入邊界點游入距離矩陣

G

.

，值得注意的是，此過程可以利用頂點拓撲序加速計算過程，由于轉化圖是有向無環圖，壓縮圖即為有向無環圖，因此在運用Dijkstra算法前，可先計算頂點拓撲序，若在計算頂點

u

到

v

的最短路徑時，

u

的拓撲序大于

v

的拓撲序，則頂點

u

到

v

的最短路徑一定為∞

.

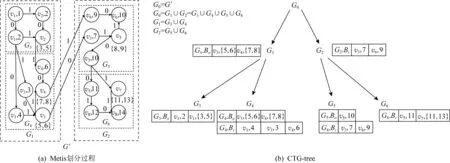
Fig. 3 Metis Partitioning and CTG-tree Construction圖3 Metis劃分以及CTG-tree構建過程

隨后，計算CTG-tree中的葉子節點對應子圖

G

，

G

，

G

和

G

的游出距離矩陣

G

.

、游入距離矩陣

G

.

和邊界點距離矩陣

G

.

.

而后，自底向上計算非葉節點對應子圖

G

，

G

和

G

的出邊界點游入距離矩陣

G

.

、入邊界點游入距離矩陣

G

.

和邊界點游出距離矩陣

G

.

.

Fig.4 Distance Matrix Index in CTG-tree圖4 CTG-tree中的距離矩陣索引

CTG-tree索引保存3部分信息：CTG-tree節點、邊界點以及距離矩陣.CTG-tree葉子節點對應子圖的頂點數目不超過閾值

θ

,每層節點數為

l

，所以CTG-tree高度為log(|

V

|

/θ

)+1，CTG-tree節點總數為

l

|

V

|

/

(

l

-1)

θ.

CTG-tree邊界點總數為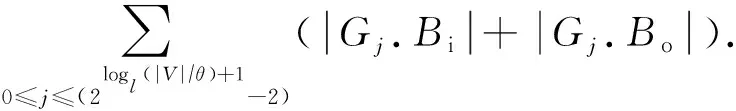

CTG-tree距離矩陣大小為

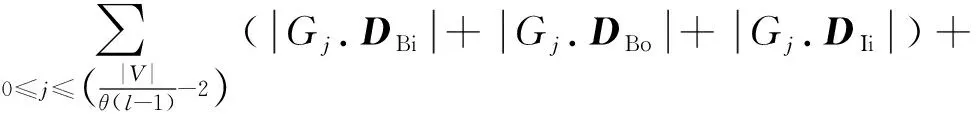
所以CTG-tree索引空間復雜度為

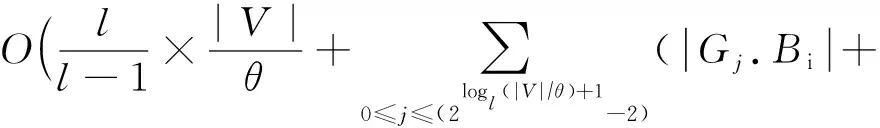
4 基于CTG-tree索引的最短路徑計算方法

本節詳細闡述在線查詢階段提出的基于層次索引CTG-tree的最短路徑計算方法.

具體的基于

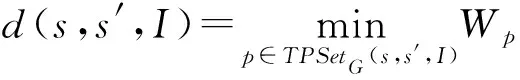
G

′構建的CTG-tree索引的最短路徑查詢算法偽碼如算法3所示

.

算法3.

最短路徑查詢算法

CTGQ

(

T

,

s

,

s

′,

I

=[

t

,

t

])

.

輸入：基于

G

′構建的CTG-tree索引

T

，查詢源點

s

，目的點

s

′，時間間隔

I

=[

t

,

t

]；輸出：

s

在時間間隔

I

內到達

s

′的最短時態路徑距離

.

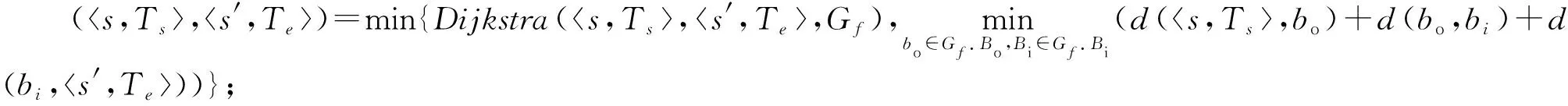
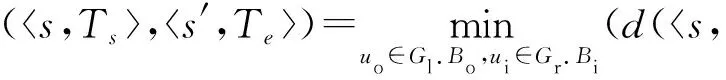
⑦ end if

，

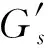
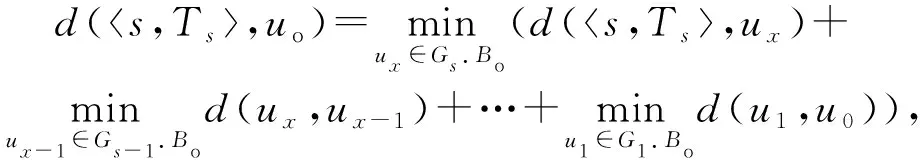
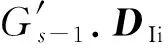
其中

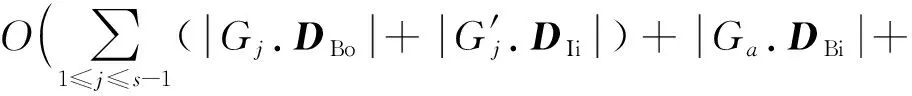
5 實驗分析

本節在真實的數據集上對所提出的CTGQ方法進行實驗測試，并與2種流行方法1-pass和TDFS進行對比，以驗證CTGQ的效率.

5.1 實驗設置

本文使用4個真實數據集進行實驗測試，分別是GTFS數據集Transit，以及SNAP公開的數據集Bitcoin，Mathoverflow，Askubuntu.Transit數據集記錄了美國科羅拉多州丹佛縣班車數據，包括班車號、班車出發時間、到達時間，停靠站點等信息.Bitcoin數據集是一個who-trust-whom網絡，網絡中的頂點表示在一個名為比特幣OTC交易平臺上使用比特幣進行交易的用戶；由于比特幣用戶是匿名的，為防止欺詐和風險用戶交易，用戶之間會進行聲譽評分，因此網絡中的邊記錄一個用戶給另一個用戶的聲譽評分以及評分時間.Mathoverflow和Askubuntu數據集均為Stack Exchange下的互動時態網絡，頂點表示用戶，從用戶

u

到用戶

v

的邊包含3種類型的互動關系:用戶

u

在時間

t

回答了

v

的問題；用戶

u

在時間

t

評論了

v

的問題；用戶

u

在時間

t

評論了

v

的回答

.

表1給出了實驗測試中用到數據集的統計信息

.

其中|

V

|,|

E

|,|

T

(

G

)|分別表示時態圖的頂點數、邊數和時態區間數

.

對于每個數據集，隨機選取500組查詢，查詢時間間隔默認為

I

=[0,+∞],報道每個算法的平均查詢時間

.

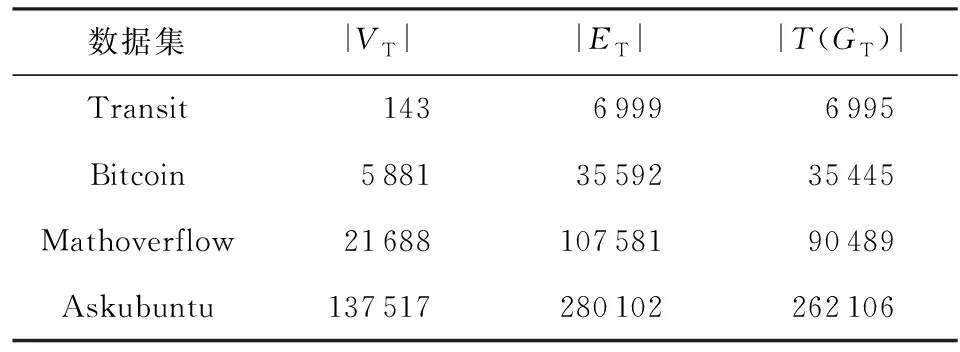
Table 1 Statistics of the Datasets表1 數據集統計信息

本文將CTGQ與1-pass和TDFS進行對比.1-pass算法和和TDFS均無需構建索引，1-pass算法在轉化圖上運用Dijkstra算法計算最短時態路徑；TDFS算法在原始時態圖上進行深度優先遍歷計算最短時態路徑；實驗測試過程中，為取得較好的索引性能和查詢性能，4個數據集Transit，Bitcoin，Mathoverflow，Askubuntu默認參數

l

=16;

θ

分別設置為128，64，256，128.本文所有實驗程序均使用C++語言編寫，實驗測試環境為一臺配置為英特爾至強CPU處理器E5-2650 v4，128 GB內存，1 TB硬盤的服務器.

5.2 實驗結果與分析

表2給出了原始數據集采用3.1節提出的規則進行轉化和壓縮后得到的轉化圖和壓縮圖的大小.與表1數據進行對比，可以看出轉化圖的頂點數是原始圖頂點數的4～97倍，轉化圖的邊數是原始圖邊數的2～4倍.相較于轉化圖，壓縮圖頂點數是轉化圖頂點的3～50倍，壓縮圖邊數是轉化圖邊數的2～3倍，說明了本文提出壓縮規則的有效性.

Table 2 Statistics of the Transformed Graph and the Compressed Graph

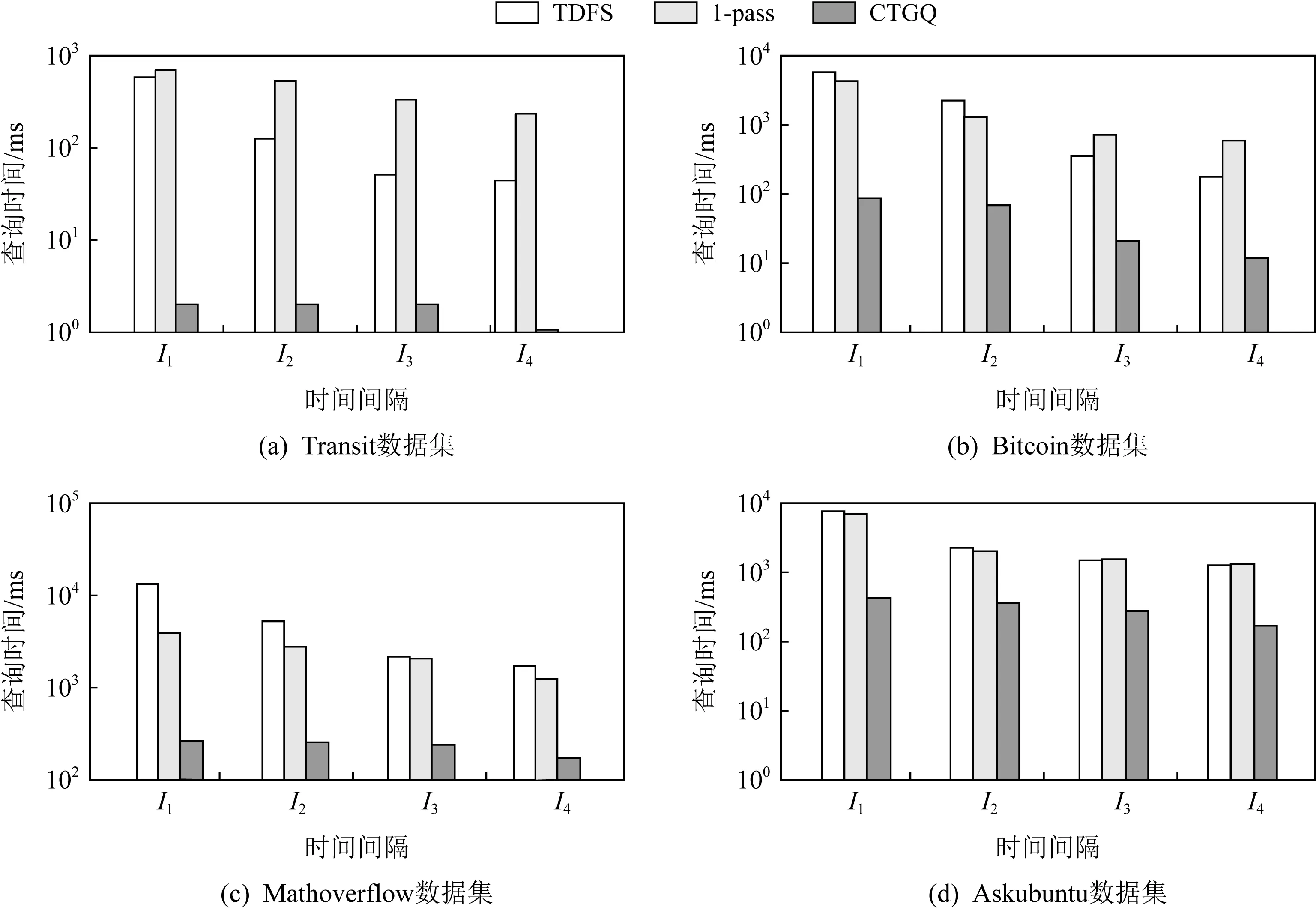
Fig. 5 Effect of Time Interval圖5 時間區間的影響

表3給出了CTG-tree索引構建時間和空間代價.可以看出，Transit數據集上構建CTG-Tree索引需要時間不足1 s；Askubuntu數據集上構建CTG-tree索引需要時間接近8 min.在4個真實數據集上，CTG-tree索引大小在20 MB到8.2 GB之間.

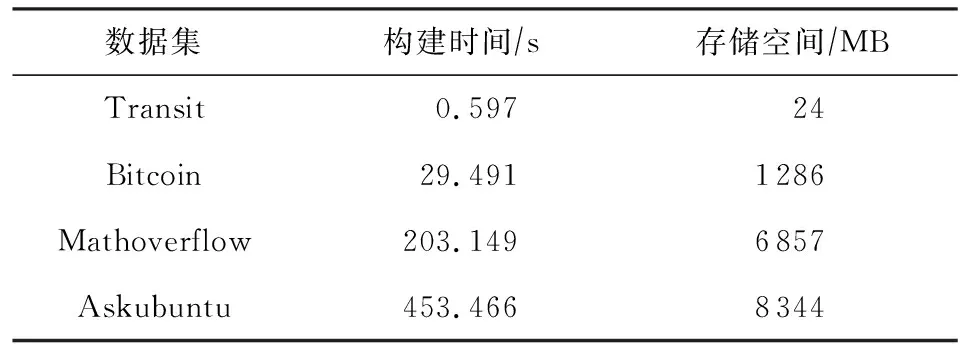
Table 3 CTG-tree Construction Cost and Space Overhead表3 CTG-tree索引構建時間和空間代價

表4給出了CTGQ,1-pass和TDFS算法在4個數據集上的平均查詢時間.由表4可以觀察出，CTGQ查詢時間比1-pass平均快1個數量級，比TDFS平均快2個數量級.這是因為1-pass算法與TDFS算法均需要在線遍歷搜索，1-pass算法需要在轉化圖上運用Dijkstra算法計算2點之間的最短時態路徑;TDFS算法在計算最短時態路徑時，由于最短時態路徑的子路徑不滿足最優子結構性質，所以TDFS需要遍歷的時態路徑是指數級的，耗時更長；而CTGQ利用了CTG-tree索引進行查詢，查詢過程中無需再遍歷壓縮圖，只需要根據CTG-tree索引矩陣即可得到結果，因此效率更高.

Table 4 Query Time表4 查詢時間 ms

本文實驗驗證了4個不同的時間間隔

I

(1≤

i

≤4)對最短時態路徑查詢時間的影響

.I

是數據集的最大時間間隔，

I

+1(1≤

i

≤3)是將

I

劃分為2個相等子區間后的第一個子區間.圖5給出了CTGQ,1-pass和TDFS算法在Transit，Bitcoin，Mathoverflow，Askubuntu數據集上的實驗結果.

從圖5可以看到，CTGQ，1-pass和TDFS的查詢時間隨著時態區間的縮減而降低，TDFS下降趨勢最為顯著.這是因為時態區間縮減時，TDFS所需遍歷的時態路徑數目大幅度減少；而1-pass和CTGQ算法在壓縮圖上計算，時態區間減小時，1-pass算法遍歷的路徑長度減小，CTGQ算法遍歷的CTG-tree矩陣索引計算量減少.

另外，從圖5還可以觀察到不同查詢時態區間下，CTGQ算法的性能始終遠遠優于1-pass和TDFS算法的性能，這與前述實驗分析結論一致.

本文考察了葉子子圖頂點數目閾值

θ

、迭代劃分子圖數目

l

對CTG-tree構建和CTGQ算法運行性能的影響.表5給出了4個數據集Transit，Bitcoin，Mathoverflow，Askubuntu在

θ

值分別設置為2，4，8，16，

l

值分別設置為32，64，128，256，512情況下的CTG-tree索引構建時間和CTGQ算法運行時間結果.

Table 5 Effects of θ and l表5 θ和l的影響 ms

首先由表5可以看到，當

l

取固定值時，CTG-tree索引構建時間隨著

θ

值增加呈減少趨勢

.

這是因為

θ

值增加，CTG-tree葉子節點對應子圖的頂點數目增多，迭代劃分產生的總子圖數目減少，相應的入邊界點、出邊界點總數減少，索引矩陣計算量減少，因此CTG-tree索引構建時間降低.其次，由表5可以看出，當

θ

取固定值時，CTG-tree索引構建時間隨著

l

值增大基本呈先降低再升高的趨勢

.

這是因為隨著

l

值的增大，CTG-tree每層節點數目增多，入邊界點、出邊界點總數先減少再增多，導致索引矩陣計算量先減小后增加.此外，當

θ

取固定值時，CTGQ算法運行時間隨著

l

值增大基本呈降低趨勢

.

這是因為，

l

值增大，CTG-tree高度降低，CTGQ算法自底向上，自頂向下遍歷層數減少.鑒于上述觀察，為取得較好的索引性能和查詢性能，4個數據集默認參數

l

=16;

θ

在數據集Transit，Bitcoin，Mathoverflow，Askubuntu上的值分別設置為128，64，256，128.

6 總 結

本文研究了時態圖最短路徑問題并提出了基于CTG-tree索引的計算方法，其主要包含預處理階段和在線查詢階段.在預處理階段，本文提出了一種無損壓縮方法和層次索引CTG-tree.其首先將時態圖轉化為普通圖，對普通圖進行無損壓縮以減小圖處理規模，將時態圖上最短路徑計算轉化為在壓縮圖上執行；而后對壓縮圖采用Metis劃分將壓縮圖層次劃分為若干個子圖，得到每個子圖的入邊界點與出邊界點集合，并基于此構建CTG-tree.CTG-tree為每個葉子節點對應子圖計算游入距離矩陣、游出距離矩陣和邊界點距離矩陣；為每個非葉節點對應子圖計算出邊界點游入距離矩陣，入邊界點游入距離矩陣和邊界點游出距離矩陣.查詢階段本文基于CTG-tree索引設計了高效的最短路徑查詢算法.最后，在真實的時態圖數據集上進行了全面的實驗，實驗結果驗證了本文所提出的基于CTG-tree索引的算法的效率.此外，設計高效的分布式時態圖最短路徑方法與增量計算算法也是一個重要且值得研究的問題，后續工作計劃對其進行深入地探索.

作者貢獻聲明

：張天明負責問題定義、方法設計、數據分析與論文撰寫修改工作；徐一恒負責數據收集與整理、實驗結果可視化工作；蔡鑫偉負責部分實驗測試和整理工作；范菁負責指導論文寫作并提出修改建議.