基于改進灰狼算法的數控車間AGV路徑規劃研究

李泓坤

（西安工業大學，陜西西安，710021）

0 引言

自動導引小車 (Automated Guided Vehicle，AGV)屬于輪式移動機器人，其以自動導引裝置為核心構件，可以按照既定的導航路線平穩行駛[1]。在數控車間等領域內，AGV主要被用作配送物料，整體表現出了操作門檻低、構造簡單的特點。但是其在實踐應用中也面臨著一些挑戰，最為棘手的就是AGV路徑規劃問題。

AGV路徑規劃直接關系到AGV的行進效率。路徑尋優算法是路徑規劃的核心，依據理論的不同，AGV路徑規劃技術可分為基于采樣的圖搜索算法、基于節點的搜索算法、基于模型的方法、基于生物啟發式算法等方法。粒子群算法、模擬退火算法、遺傳算法等都是典型的啟發式算法。生物啟發式算法相較于傳統路徑規劃算法，減少了對數學模型的依賴，全局尋優能力強，在AGV規劃研究中已經得到大量的實際應用。

灰狼優化 (grey wolf optimization， GWO)[2]算法作為一種生物啟發算法，具有結構簡單、需要設置的參數少和在實驗編碼中易實現等優點。然而，過去普遍采用GWO算法應對AGV的路徑規劃問題，此算法與生俱來的一些缺陷難以保證機器人的運動效率，會造成碰撞的可能，這些缺陷主要是易陷入局部極值、全局勘探與局部開發失調、初始種群過于單一等。

本課題結合GWO算法的上述缺陷，提出了一種改進灰狼優化算法（IGWO），在求解AGV全局路徑規劃問題時，通過改良，使得灰狼優化算法能夠更好地適應數控車間環境，并基于此給出穩定的路徑尋優結果，這樣就能確保AGV始終選擇最佳路徑行駛，從而保證導航的準確性，并避免碰撞。

1 灰狼算法

GWO算法屬于新型群體智能優化算法，其基本原理是對灰狼群體在自然界內生存時所存在的捕獵行為和社會等級機制進行模擬，對于此算法而言，灰狼種群內任意灰狼都是一個可能的候選解，群體中包含的的最優解、次最優解、第三最優解分別用α，β，δ表示，其他候選的解都用ω表示。然后我們用D 表示灰狼種群的大小，用D 表示搜索空間，那么就代表第D維空間內第i只灰狼的位置。灰狼群體通過式（1）逐漸接近并包圍獵物：

2 改進灰狼算法

2.1 基于混沌的種群初始化方法

skew tent映射是一種由簡單的確定性系統產生的隨機性序列，混沌映射被用于生成混沌序列。在優化領域，混沌映射可以用于替代偽隨機數生成器，生成0到1之間的混沌數。經過實驗證明，利用混沌序列進行種群初始化、選擇、交叉和變異等操作會影響算法的整個過程，而且常常能取得比偽隨機數更好的效果。

本文先初始化處理了目標種群，具體是基于skew tent映射得到混沌序列實現的，這樣就可以確保解空間的信息被初始群眾個體充分利用，同時確保最終解的完整性，其函數式如下所示[3]：

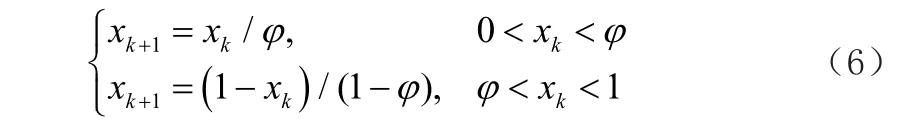
當φ∈(0,1)且x∈[0,1]時，系統處于混沌狀態。

2.2 IGWO算法步驟

結合如上分析，得出下表1所示的高效灰狼優化算法（簡稱IGWO）的詳細步驟。

算法 1 IGWO 算法begin算法參數設置：N-種群大小；t -距離控制參數a的初始值；a max -最大迭代次數；ainitial-距離控制參數a的終止值。基于skew tent混沌初始化得到final灰狼種群對群體內所有個體的適應度進行求解，{X i N i , 1,2, ,= …}{f X i N( )i , 1,2,,= …}，然后對最

優個體、次最優個體、第三最優個體α、β、δ進行記錄，用X β表示其對應位置。)d o f o r i=1 t o N d o f o r j=1 t o D d o對距離控制參數a的值進行求解。代入公式（2）和（3）對參數A和C的值進行求解。代入公式（6）完成個體位置的更新。e n d f o r e n d f o r對群體內所有個體的適應度進行求解，w h i l e(t＜t m a x{f X i N( )i , 1,2, ,= …}然后對最優個體、次最優個體、第三最優個體α、β、δ進行記錄，用X β表示其對應位置t=t+1;e n d w h i l e e n d

2.3 路徑尋優約束條件與適應度函數

選擇最優路徑的期間，假設機器人的某條行駛路線便是任意灰狼捕獵期間位置更新時對應的坐標集，IGWO算法按照優化策略，在路徑集合當中選出一條與約束條件高度匹配的路徑，約束條件如下。

(1)路徑連續性條件

移動路徑不能有迂回狀況，即節點的縱向坐標或是橫向坐標，相對于下一個節點兩者只能有一個是在單調遞增，假設機器人由當前節點(x1, y1)移動到下一節點(x2, y2)應至少滿足(x2＞x1)或(y2＞y1)。

(2)環境邊界與障礙物約束條件

移動路徑必須限定在固定圖幅邊界的柵格區域內，且移動路徑節點及節點間的連線禁止穿過障礙物柵格。

(3)目標路徑最短條件

在滿足約束條件(1)、(2)下的諸多柵格位置中，第j( j = 1 ,2,...Ny)行柵格應選橫坐標最小值i( 1 ＜ i＜Nx)作為最終路徑節點(xi, yi)，以達到路徑最短條件，即IGWO算法規劃結果中適應度函數須取最小值。

數控車間環境在路徑尋優過程中，以對角線距離作為適應度函數。

3 AGV運行環境建模

本文采用柵格地圖表示法[5]表示數控車間環境，將數控車間中 AGV 運行環境視為由多柵格組成的矩形，且每個柵格大小相同。考慮到數控車間下機床對AGV運行路徑的影響，對機床柵格進行膨脹處理。后續驗證采用八方向搜索節點方法，即AGV可到達相鄰位置的8個節點。

通過以上研究，基于數字仿真軟件測試平臺構建了一個37×23數控車間柵格地圖。其中黑色為機床位置，紅色為AGV充電位置，綠色為車間倉庫位置。

4 仿真實驗結果與分析

本文以計算機作為仿真實驗平臺，其CPU型號為Intel(R) Core(TM) i5-10200H，內存為 16GB，處理器主頻為 2.4 GHz，操作系統為 Windows 10，采用 MATLAB R2021b 軟件進行仿真操作。

下表1列出了本次實驗的算法參數，以應用路徑規劃時對比算法所需搜索空間和對比算法所在原文獻為依據對種群大小、最大迭代次數進行設置，以保證所得結果的準確性與客觀性。

表1 仿真實驗中的算法參數設置

4.1 路徑規劃仿真

為了驗證本文提出的IGWO算法有效性，通過對柵格地圖設置不同的AGV初始位置，物料轉送位置和最終停車位置，從尋優效率、路徑長度等優化性能方面橫向對比的GWO算法和IGWO算法的仿真試驗結果，實驗次數為30。

PSO算法沒無法在全局內搜索最優路徑，而且路徑尋優收斂效率較低，期間還出現了搜索停滯的現象（陷入局部極值導致）。在迭代前期，GA算法有著十分可觀的收斂速度，但與其他啟發式算法相比，其也出現了局部收斂的問題，而且比較頻繁；SA算法也有著理想的收斂速度，全局路徑規劃表現較好，但仍存在多次實驗所得最優路徑值不穩定等問題；GWO算法不但在初始階段擁有理想的收斂速度之外，中后期搜索還協調了局部開發。由此可見，本文提出的IGWO算法有效彌補了傳統GWO算法優化方面的缺陷，具有十分理想的搜索能力和收斂能力。

從表2得出：相較于傳統GWO算法，本文提出的IGWO算法平均路徑長度更短且得到穩定性更強的結果，算法同時具有理想的收斂速度，因此尋優耗時也變相縮短了。

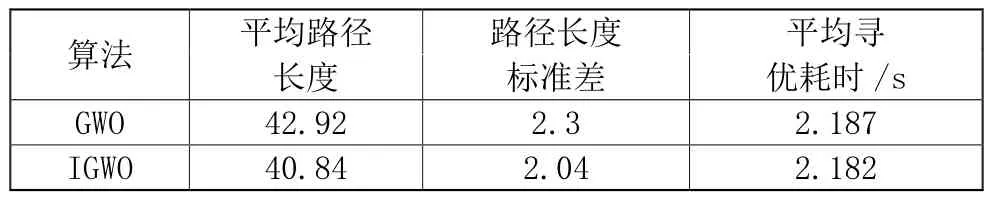
表2 環境1中30次實驗的算法性能對比

5 結論

本文對灰狼算法進行改進，以求解數控車間AGV全局路徑規劃問題，基于路徑規劃仿真實驗結果，得到幾點結論，具體如下：

（1）本文提出的IGWO算法通過引入Tent混沌映射來保證灰狼種群初始化的均勻性，這樣就能很好地克服傳統GWO算法初始群眾分布不均的問題，同時還能使得算法在路徑尋優初期的收斂速度得以提升，在路徑尋優期間，此算法在綜合勘探和避障方面的表現十分出色，一定程度上彌補了傳統GWO算法全局算法與局部開發不協調的缺陷，使得算法在路徑尋優最后階段能較為準確地鎖定全局最優解。

（2）全局路徑規劃仿真實驗表明，在數控車間場景下，IGWO算法計算所得的路徑有效、合理。相對比于傳統GWO算法、GA算法、SA算法、PSO算法，本文IGWO算法在路徑尋優能力、收斂效率、尋優結果穩定性等方面具有一定的優越性。

（3）本文提出的IGWO算法相較于傳統啟發式算法具有結構簡單、計算復雜度較小、全局搜索能力較強等優勢。本文所提的各項改進策略可為其他啟發式群智能算法的優化改進以求解全局路徑規劃問題提供參考。