粗糙表面接觸剛度模型的研究進展

艾延廷，解松霖,劉玉，田晶，趙丹，劉俊男

（1.沈陽航空航天大學航空發動機學院，2.遼寧省航空推進系統先進測試技術重點實驗室：沈陽 100136；3.中國航發四川燃氣渦輪研究院，成都 610550）

0 引言

相互接觸的零件之間的結合部分被稱為“機械結合面”，航空發動機機匣安裝邊螺栓連接結構便是裝配形成的機械結合面。機械結合面之間的接觸并非光滑的面與面之間的接觸，而是由許多微凸體之間的相互接觸構成的[1]，導致2個粗糙表面接觸時的實際接觸面積總是小于名義接觸面積[2-3]。在航空發動機中這種結合面分布廣泛，結合面間的接觸剛度對航空發動機整機結構的穩定性、可靠性有著至關重要的影響[4-5]，準確計算結合面間的接觸剛度在航空發動機設計中尤為關鍵[6-7]。為了準確計算粗糙表面間的接觸剛度，需要對粗糙表面間的微凸體接觸進行建模。粗糙面接觸模型主要分為解析模型和有限元模型。目前大部分粗糙表面接觸模型都屬于解析模型，表征粗糙面形貌的解析方法主要分為統計描述和分形描述。大部分接觸剛度模型主要根據統計學理論接觸模型[8-9]及分形理論的接觸模型[10-11]建立。

關于粗糙表面間接觸建模已有許多研究成果[12-13]。Bhushan[14]于1996年將粗糙表面上的單個微凸體間相互接觸的問題分為彈性解析模型和彈塑性有限元模型來分類敘述；賀林等[15]于同年對粗糙面接觸分形模型進行了概述；Bhushan[16]于1998年將之前建立的粗糙表面接觸模型按照微凸體的輪廓形狀和分布高度分為2類進行了討論；Adams等[17]在2000年將微凸體間的接觸分為單個微凸體的接觸和多個微凸體的接觸，特別介紹了接觸面之間作用力（即粘著力）的產生；魏龍等[18]于2009年對粗糙表面接觸模型的發展進行了總結，分別介紹了Hertz接觸模型、統計學接觸模型和分形接觸模型的優劣性；Ghaednia等[19]于2017年分別按照微凸體的幾何形狀和加載方式對單個微凸體接觸模型進行了評述。

隨著航空發動機技術的發展，發動機結構設計變得尤為關鍵。機匣做為發動機主要承力部件，需要具有足夠的剛度來保證發動機穩定運行。由螺栓連接所構成的機匣安裝邊作為機匣中最重要的一環，可有效地提升其接觸剛度，對整個發動機結構穩定性有著至關重要的影響。接觸模型的發展目前已較為完善，但是關于接觸剛度模型的綜述性文章仍然非常匱乏。

本文對國內外不同的粗糙面接觸剛度模型的發展歷史和研究現狀進行了總結，重點對接觸剛度的計算進行了詳細闡述。分析了現有結合面接觸剛度模型的不足，展望了接觸剛度模型的發展趨勢。

1 粗糙表面的描述和表征

1.1 單個微凸體接觸

要建立完整的粗糙表面接觸模型，首先要清楚粗糙表面上的單個微凸體受載荷的變形規律，該問題被稱為赫茲接觸[20-22]，是微觀接觸力學中的一個重要問題，被眾多學者所關注和研究。研究發現，粗糙表面上的單個微凸體在變形過程中共經歷3個階段：相互接觸的微凸體首先進入彈性變形階段，隨著載荷的增加逐漸進入彈塑性變形階段，當載荷達到一定值時進入塑性變形階段。

當微凸體處于彈性變形階段時，由赫茲接觸理論可知，接觸面積ae、接觸載荷fe、最大接觸壓力pem、平均接觸壓力pea分別為

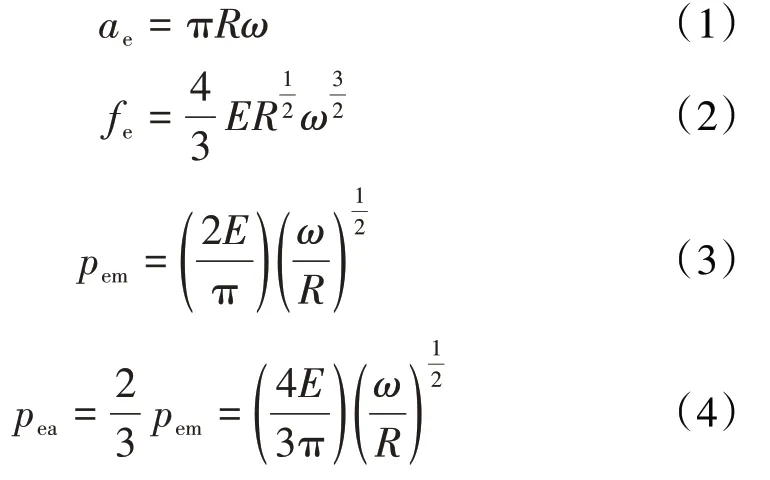
式中：R為相對曲率（R=1/R1+1/R2）；R1、R2分別為2個微凸體的半徑；E為等效彈性模量，1/E=（1-υ12）/E1+（1-υ2

2）/E2，E1、E2和υ1、υ2分別為2個微凸體的彈性模量和泊松比；ω為微凸體的變形量。

當微凸體所受載荷大于屈服極限時，塑性變形開始在微凸體內部產生，此時微凸體處于彈性變形和塑性變形共存的階段，即彈塑性階段[23-25]。大多數彈塑性接觸模型都是采用有限元方法建立簡化的球體與光滑的平板的接觸模型進行分析[26-28]。眾多學者將彈塑性變形分為3類，即壓平模型、壓入模型和綜合模型[29-31]。目前還沒有從彈塑性變形基本理論推導出閉合解[32-33]。

當載荷達到一定值后，塑性變形由原來的只存在于某一區域迅速擴展至整個微凸體，這種狀態被稱為完全塑性變形階段[34-35]。通常采用Tabor[36]、Abbott等[37]的試驗結果來計算微凸體處于完全塑性變形階段時的接觸面積ap、平均接觸壓力ppa和接觸載荷fp

式中：H=2.84σy為材料的硬度，σy為材料屈服強度。

1.2 粗糙面表面接觸

為了準確地分析粗糙表面間接觸行為和接觸特性，需要建立與真實物體表面形貌相近的接觸模型，表面形貌即粗糙表面微凸體的數量、分布高度、曲率半徑、輪廓形狀和位置等參數[38]。接觸模型主要分為解析模型和有限元模型，其中解析模型是眾多學者主要研究的方向，解析模型又具體劃分為統計描述模型和分形描述模型。

1.2.1 解析模型

（1）統計學描述。應用統計方法描述粗糙表面最大的特點是可以體現其各微凸體高度的隨機性[12]，描述方法可分為隨機過程描述和微凸體高度分布描述。隨機過程描述是指微凸體的分布高度到基體的距離是隨機的，這一距離可用某一特定的分布函數和自相關函數來描述，由此表征粗糙表面的形貌特征；微凸體高度分布描述則是假設粗糙表面上所有微凸體的高度和曲率滿足某種統計學規律，通過特定的統計分布函數來確定形貌特征。由此可見，微凸體高度分布描述是對隨機過程描述的一種簡化，將包含多尺度信息的粗糙表面簡化為單一尺度的粗糙表面。應用統計描述表征粗糙表面的過程較為簡單，極大程度縮短了求解過程，有利于進行粗糙表面間的接觸建模，但其不能完全表征粗糙表面所有的形貌特征，無法表征一個確定的粗糙表面。

（2）分形描述。隨著對粗糙表面研究的不斷深入，發現實際物體的粗糙表面的形成是一個非平穩的隨機過程[39]，粗糙表面上的微凸體的高度分布與采樣設備的分辨率相關，將粗糙表面放大后，可以看到在任意尺度下粗糙表面的形貌特征基本不會發生變化，這就是粗糙表面形貌的自相似性及尺度不變性。因此，可采用分形參數（分形維數和特征尺度系數）來描述粗糙表面的形貌特征。分形理論所描述的物體形貌特征不受空間的束縛，更加接近客觀物體的真實屬性與狀態，更加符合客觀物體的多樣性與復雜性。應用分形描述的方法來建立粗糙表面形貌特征是分形接觸模型的基礎，先通過儀器提取物體粗糙表面真實形貌數據，再基于分形理論計算得到與物體粗糙表面形貌相近的分形參數，由分形參數確定粗糙表面的形貌特征，進而建立粗糙表面接觸模型。

1.2.2 有限元模型

隨著計算機水平的不斷進步，有限元仿真方法逐漸被用于微觀粗糙面建模中[40-42]。有限元模型可以更直觀地觀察接觸面的微凸體分布、應力分布，其結果更加真實。有限元模型雖然彌補了解析模型的一些不足，但是想要完整地描述粗糙面形貌特征，就必須進行非常細致的網格劃分，這樣會大幅增加計算時間和計算難度。目前有限元方法通常僅適用于微小的接觸模型，對于跨尺度的模型仍存在一些挑戰。

2 基于統計描述的粗糙面接觸剛度模型

2.1 GW模型

關于粗糙表面接觸，Greenwood和Williamson[43]在1966年基于赫茲接觸理論提出的GW模型是統計接觸模型的典型代表，為其后學者研究粗糙表面間的接觸問題奠定了理論基礎，至今仍被廣大學者廣泛使用[44]。

GW模型用1個粗糙面和1個光滑剛性平面等效替代2個相互接觸的粗糙表面，其表面上所有微凸體間互不影響，并將所有微凸體等效成具有相同的曲率半徑的球形微凸體，微凸體頂點高度分布滿足高斯分布，GW模型只針對彈性變形進行了分析，并提出了塑形指數作為彈性、塑形接觸狀態的區分條件。微凸體與光滑平面的接觸如圖1所示。圖中z為某個微凸體與微凸體平均高度之間的距離，d為微凸體平均高度與光滑平面之間的距離，h為粗糙表面輪廓線平均高度與光滑平面之間的距離，微凸體的變形量ω=zd。φ（z）dz為滿足高斯分布的微凸體高度分布函數。

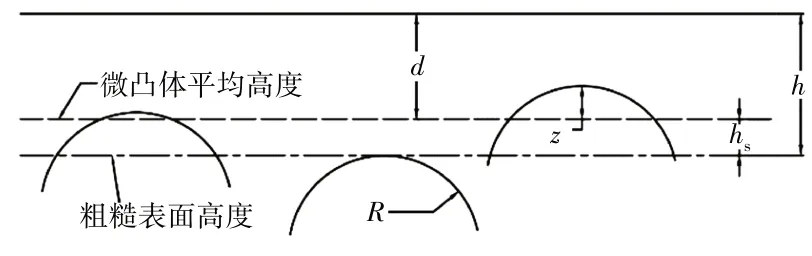
圖1 微凸體與光滑平面的接觸

根據赫茲接觸理論，微凸體總數量為

式中：η為微凸體接觸面積密度函數；An為名義接觸面積。

當微凸體變形量ω＞0，即z＞d時，微凸體將與剛性平面發生接觸，接觸的微凸體總數為

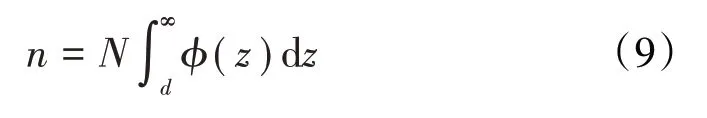
根據赫茲接觸理論，總的接觸面積A、接觸載荷F和接觸剛度K分別為

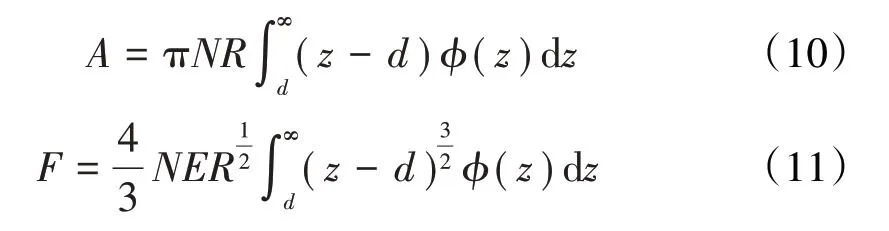
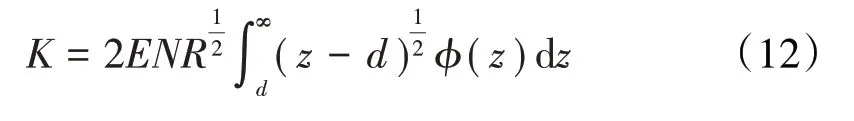
雖然GW模型為其后眾多學者廣泛借鑒，但仍有許多不足之處：（1）只考慮了微凸體間的彈性作用，忽略了微凸體間的彈塑性及塑性作用；（2）忽略了微凸體間的相互作用，認為各微凸體相互獨立、互不影響；（3）將所有微凸體的曲率半徑簡化為某一恒定的值，這是不符合實際情況的。隨著研究的進一步深入，不斷有學者對其進行改進和補充。

2.2 考慮彈性及塑性的統計學接觸剛度模型

1987年，Chang等[45]在GW模型的基礎上建立了CEB模型，將微凸體的變形劃分為彈性變形階段和塑性變形階段2個階段，給出了微凸體彈性變形與塑性變形的臨界接觸變形量ωc，彌補了GW模型只考慮微凸體彈性變形的不足。同時根據單個微凸體在塑性變形過程中體積恒定，給出了單個微凸體處于塑性變形階段時的接觸面積ap、接觸載荷fp，計算得到接觸剛度kp

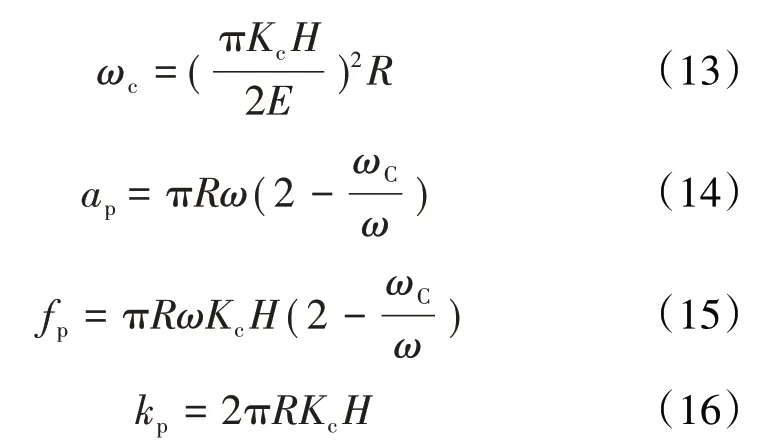
式中：Kc=0.454+0.41μ，為最大接觸壓力因子，μ為較軟材料的泊松比。

隨后根據發生接觸的微凸體總量，給出了總的接觸面積A、總載荷F，計算得到總接觸剛度K

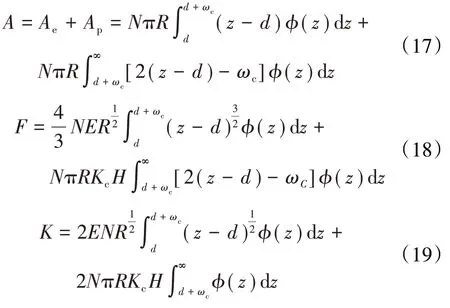
式中：Ae、AP分別為彈性接觸面積、塑性接觸面積。

CEB模型只考慮了彈性變形及塑性變形，忽略了由彈性過渡到塑性時的彈塑性變形，導致臨界點處不連續，接觸壓力直接從2KH/3突然跳躍至KH。使得接觸剛度在由彈性變形向完全塑性變形轉化時是不連續的。

2.3 考慮彈性、彈塑性及塑性的統計學接觸剛度模型

為彌補CEB模型的不足，2000年，Zhao等[46]基于CEB模型建立了ZMC模型，將微凸體變形劃分為彈性階段、彈塑性階段、塑性階段3個階段。基于4階多項式和對數函數推導出微凸體處于彈塑性變形階段時的接觸面積、平均接觸壓力。該方法實現了平均接觸壓力在彈性屈服點和臨界塑性點的連續性，但仍然不具備光滑性，因此該模型建立的接觸剛度模型在臨界點處是不連續的。

2002年，Kogut和Estion[47]在ZMC模型的基礎上采用有限元方法計算了單個球體與剛性平面的接觸，并應用冪函數擬合了有限元近似解。基于有限元數據，將微凸體變形分為彈性階段、第1彈塑性階段、第2彈塑性階段、塑性階段4個階段。4個階段臨界處對應的微凸體臨界變形量分別為ωc、6ωc、110ωc。即當0＜ω＜ωc時，微凸體處于彈性變形階段；當ωc＜ω＜6ωc時，微凸體處于第1彈塑性變形階段；當6ωc＜ω＜110ωc時，微凸體處于第2彈塑性變形階段;當110ωc＜ω時，微凸體處于完全塑性階段。處于彈塑性階段所對應的接觸載荷、接觸剛度分別為

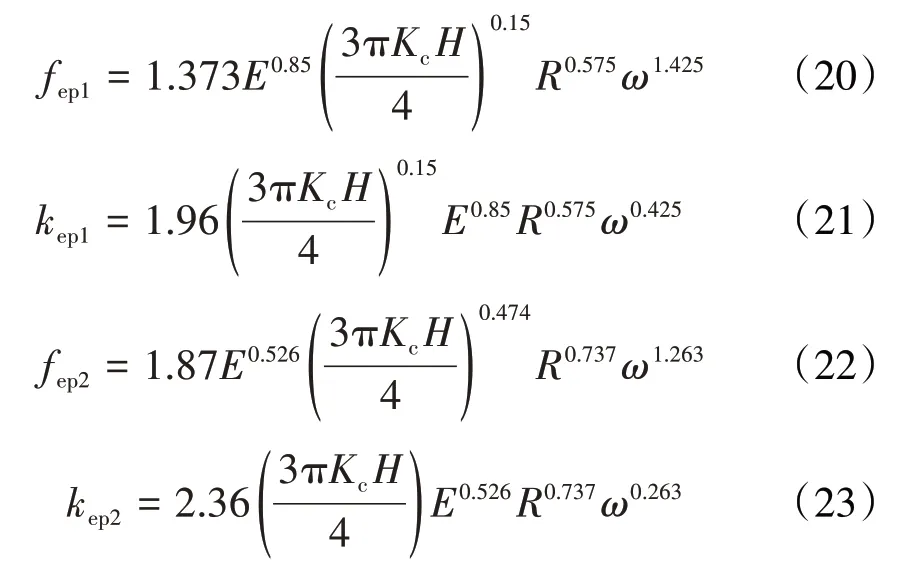
式中：fep1、kep1和fep2、kep2分別為微凸體處于第1、2彈塑性階段時的接觸載荷、接觸剛度。

根據GW模型中給出的總的接觸載荷、接觸剛度思路，可以計算出KE模型總的接觸載荷、接觸剛度

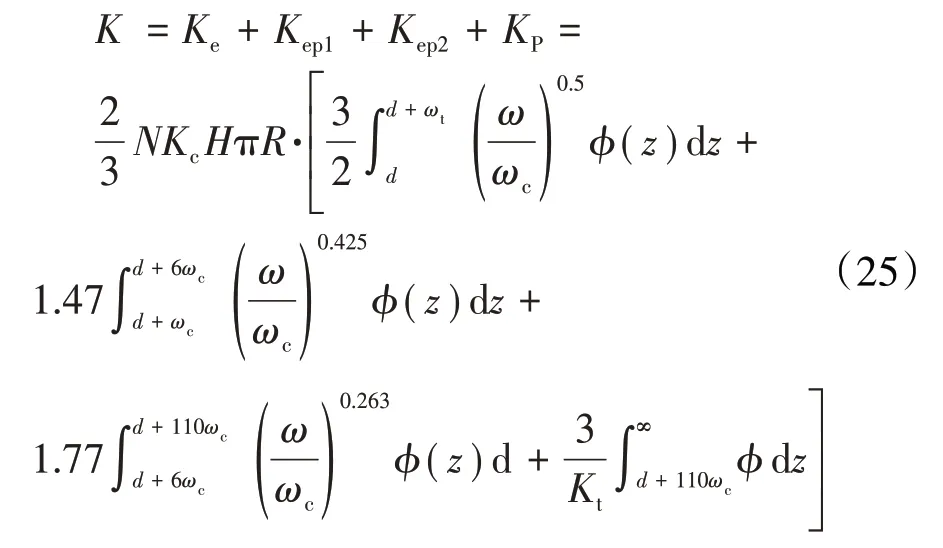
2017年，田小龍等[48]考慮了微凸體間的相互作用，應用勒夫方程和圣維南原理推導出的接觸面各參數（接觸載荷、局部變形、表面壓強）和材料屬性之間的函數關系，將其代入微凸體變形量表達式中，得到了更接近真實情況的變形量表達式，將其帶入ZMC和KE模型中，得到了考慮微凸體之間相互影響的粗糙面接觸剛度模型，ω在彈性階段的表達式為

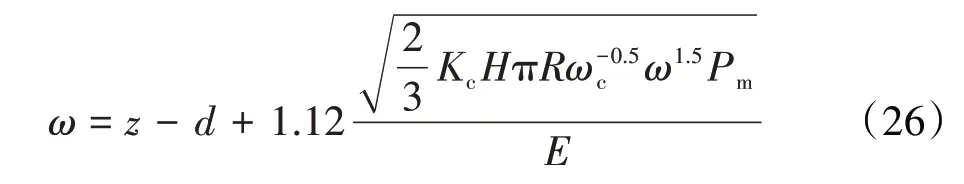
在第1彈塑性階段的表達式為

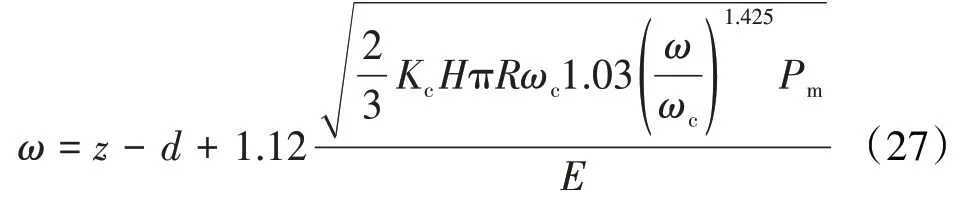
在第2彈塑性階段的表達式為

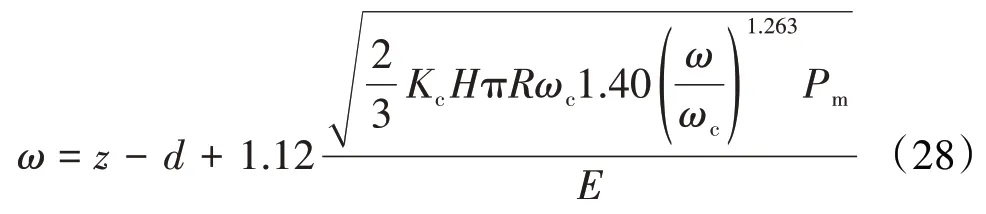
在塑性階段的表達式為

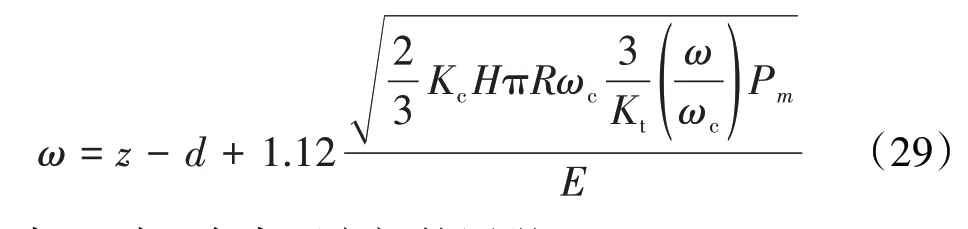
式中：pm為2個表面之間的壓強。

Jackson等[23]采用較KE模型有著更精密網格的有限元模型，建立了新的單個微凸體與剛性光滑平面接觸的有限元模型，即JG模型，該模型考慮了微凸體變形過程中微凸體硬度變化、幾何尺寸變化及材料屬性的影響。該模型發現微凸體的彈性變形可在[0，1.9ωc]內發生，在微凸體變形量比較小時，接觸載荷、接觸面積、接觸剛度變化規律與Hertz接觸理論基本一致。但JG模型并沒有考慮微凸體開始發生塑性變形時的臨界接觸點。

2.4 具有連續光滑特性的統計學接觸剛度模型

2012年，Brake[49]提出了一種微凸體接觸載荷為光滑連續的粗糙面模型，應用了Hermit多項式插值函數，但由于Hermit多項式階次過高，導致彈塑性變形階段的微凸體接觸載荷與變形量的關系出現震蕩，從而導致接觸剛度數值也出現波動，甚至出現剛度小于0的情況，這是不符合實際情況的。

2021年，李玲等[50]應用Hermit插值方法，使接觸載荷在彈性轉變為彈塑性臨界點及彈塑性轉變為塑性臨界點處光滑且連續，將接觸載荷轉換到對數坐標系，減小插值區間，進而降低了由Hermit插值多項式階次過高帶來的震蕩。建立了單一微凸體連續光滑的接觸剛度模型，然后基于統計學方法進行無量綱處理，得到了結合面接觸剛度模型。其單個微凸體彈塑性變形區接觸剛度為

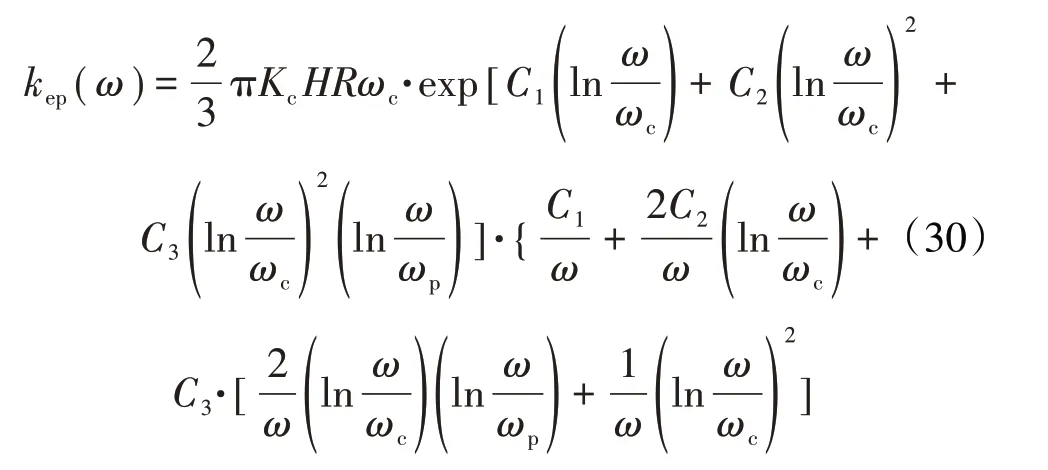
式中：C1、C2、C3為Hermit多項式系數；ωp=110ωc。

基于統計描述所建立的接觸模型，有利于描述不同粗糙表面的形貌特征，但由于粗糙表面的不確定性，無法準確地分析粗糙表面的接觸特性。在一定測量條件下得到的統計學參數具有局限性，不能表征完整的粗糙表面，這是由于粗糙表面具有多尺度特性所造成的。

為了考慮粗糙表面的多尺度特性，大多數學者采用分形理論來建立接觸模型，相較于統計描述更能夠反映出粗糙表面的多尺度特性。

3 基于分形描述的粗糙面接觸剛度模型

3.1 MB模型

1990年，Majumdar與Bhushan[51]共同提出了基于分形幾何理論構建的粗糙表面接觸模型，即MB模型，這種模型將實際2個粗糙表面之間的接觸簡化為1個光滑的剛性理想平面與1個粗糙平面的接觸，并且忽略了材料硬度隨微凸體深度的變化且假設各微凸體相互獨立，不過這一粗糙表面具有分形特性。

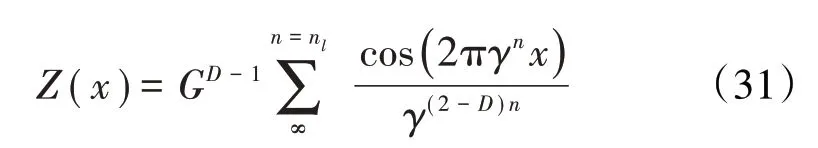
式中：D為分形維數；G為特征尺度系數；x為表面輪廓位置坐標；Z為表面輪廓高度坐標；γn為粗糙表面頻率參數。

該模型以W-M分形函數（W-M函數描述的粗糙表面與光滑平面接觸如圖2所示）及海洋島嶼面積分布規律為基礎，研究了單個微凸體變形處于彈性階段和塑性階段的變形機制，獲得了較為真實的微凸體接觸面積與接觸載荷之間的關系。給出了微凸體接觸面積分布函數n（a）及粗糙表面與剛性平面總的截面積公式，為今后學者的研究奠定了理論基礎。

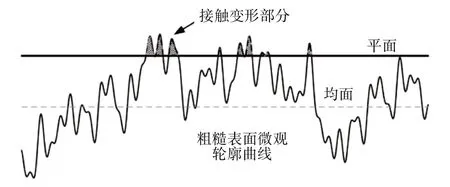
圖2 W-M函數描述的粗糙表面與光滑平面接觸

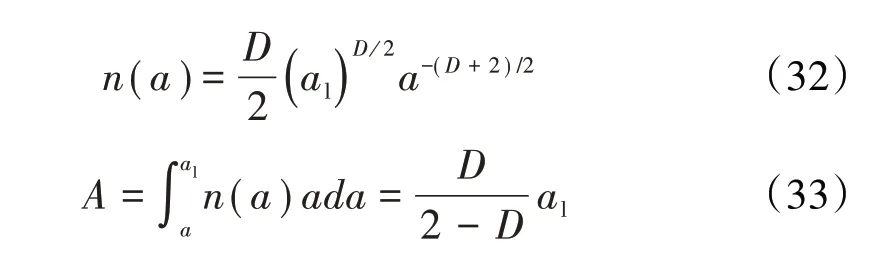
式中：a為粗焅表面單個微凸體接觸面積，al為粗糙表面單個微凸體最大接觸面積。

Wang等[52]基于MB模型，考慮了溫度對微凸體面積分布密度函數的影響，修正了微凸體面積分布密度函數，但忽略了單個微凸體緩慢滑動狀態。根據單個微凸體接觸面積隨溫度的變化關系及接觸面上的最高溫度，修正了MB接觸模型，得到了新的彈性、塑性接觸模型。

3.2 考慮彈性、塑性的分形接觸剛度模型

2000年，張學良等[53-54]基于MB分形模型，假設粗糙表面各向同性，各微凸體間相互獨立，考慮了微凸體塑性變形階段對接觸剛度的影響，給出了微凸體由塑性變形變為彈性變形時的臨界接觸面積ac，

由分形理論可知，當a＜ac時微凸體發生塑性形變；當a＞ac時微凸體發生彈性形變。這顯然與統計學模型相互矛盾。

Morag等[55]針對這一現象給出了解釋，當微凸體接觸面積非常小時，微凸體會受到1個較大的接觸壓力。因此，接觸面積小于臨界值的微凸體受到的壓力較大，更容易發生塑性變形；而接觸面積大于臨界值的微凸體受到的壓力較小，不會發生塑性變形。目前為止，這種非常規的接觸行為依然被許多研究者所采用。

根據上述理論，單個微凸體與剛性光滑平面接觸的法向接觸剛度kn、切向接觸剛度kt分別為

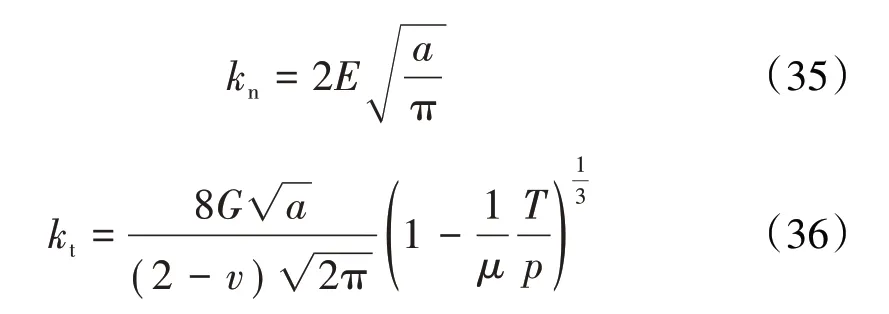
式中：G為接觸面2種材料的等效剪切模量；υ為接觸面2種材料的泊松比；μ為摩擦系數；P為微凸體所受的法向載荷；T為微凸體所受的切向載荷。

根據微凸體面積分布函數得到總的接觸剛度為

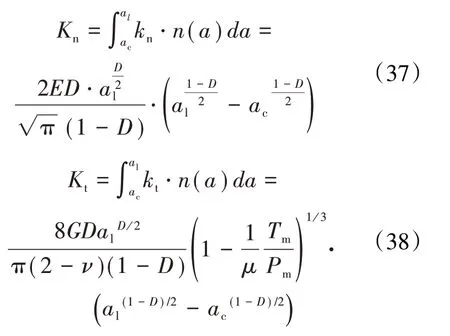
2009年，溫淑花等[56-57]基于分形理論引入以微凸體變形位置截面積a'為變量的接觸面積分布函數n（a'），建立了考慮區域擴展因子的結合面接觸剛度分形模型

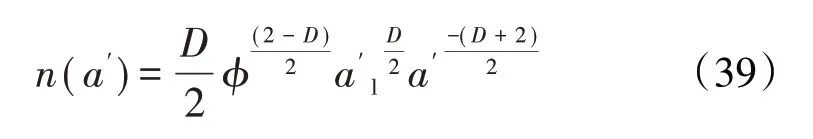
式中：φ為區域擴展因子；a'為微凸體接觸截面積，其與真實接觸面積之間的關系為a'=2a。

整個結合面的法向接觸剛度、切向接觸剛度分別為

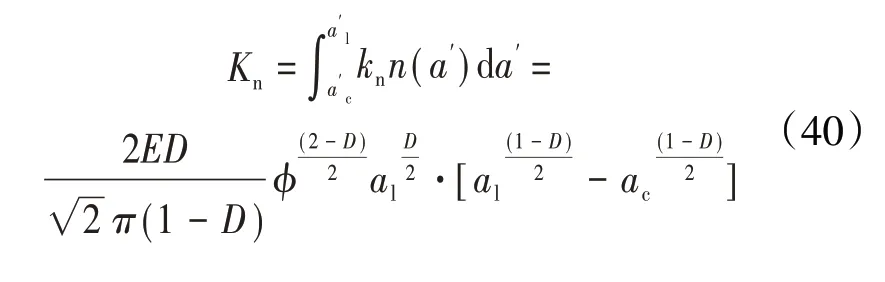
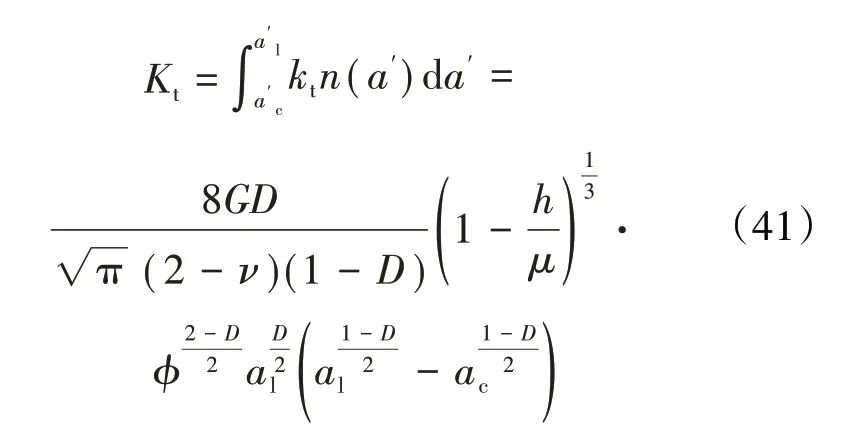
3.3 考慮彈性、彈塑性及塑性的分形接觸剛度模型

2015年，張學良等[58]基于分形理論、MB模型及KE模型，分別計算了微凸體變形處于4個階段（彈性變形階段、第1彈塑性變形階段、第2彈塑性變形階段、塑性變形階段）時的接觸剛度，建立了更符合實際情況的結合面法向接觸剛度分形模型。單個微凸體不同階段的法向剛度分別為

彈性階段的法向剛度

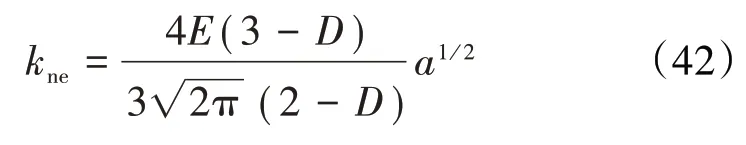
第1彈塑性階段的法向剛度

第2彈塑性階段的法向剛度

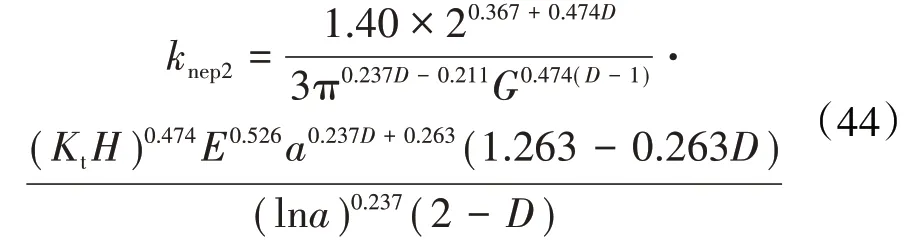
處于完全塑性的微凸體不具有法向剛度，則結合面總的法向接觸剛度為

式中：ac為微凸體變形量為ωc時的接觸面積。

2018年，陳建江等[59]基于分形理論建立了一種粗糙表面加卸載力學解析模型。推導出了單個微凸體變形處于不同階段（彈性變形階段、彈塑性變形階段和塑性變形階段）的條件。引入了頻率指數，并總結了不同頻率指數所對應的微凸體面積密度分布函數。王顏輝等[60]基于上述理論得到了微凸體處于各變形臨界階段時頻率指數的大小，建立了頻率指數大小不同時的結合面接觸剛度模型。

4 有限元接觸剛度模型

隨著有限元技術的發展，越來越多的學者開始采用有限元方法建立接觸模型，彌補解析模型的不足。

2012年，楊國慶等[41]通過3D粗糙表面數字化表征方法，獲得了具有不同統計特征的高斯或非高斯粗糙表面，并分析了其接觸特性。

2017年，孫偉等[61]基于有限元方法提出了一種結合面法向接觸剛度多尺度計算方法。該方法在儀器測量的形貌數據基礎上，采用小波分析技術獲取了更加真實的形貌，并基于有限元微觀接觸分析建立了局部壓強與基礎剛度的關系。基于有限元宏觀分析得到壓強分布，進而得到結合面接觸剛度。實現了接觸剛度從微觀到宏觀的跨越。

2018年，吳少雷等[62]基于Matlab與Ansys構建出3維隨機表面，簡化了粗糙表面建模過程，完成了粗糙表面參數化建模。

2021年，伍偉敏等[63]基于車削運動原理，采用Abaqus建立了3維車削粗糙表面接觸模型，得到了法向接觸剛度有限元結果。為計算車削表面法向接觸剛度提供了一種新方法。

5 未來研究方向

隨著航空發動機技術的逐漸進步，發動機整機的穩定性愈發重要，如何提高發動機穩定性將成為制約發動機技術進步的關鍵因素。本文從接觸剛度的角度出發，提出以下3個研究方向，為今后航空發動機技術發展提供借鑒。

（1）納米級粗糙表面接觸剛度模型。隨著機械零件加工技術的不斷進步，零件的尺寸已經達到納米量級，零件的尺寸與微凸體的尺寸將同處于這一量級，材料的剛度性能將呈現出微尺度效應，在今后的建模過程中，如何考慮這種尺度效應，是接觸剛度建模的重要研究方向。

（2）考慮基體變形的粗糙表面接觸剛度模型。不管是統計描述接觸剛度模型還是分形描述接觸剛度模型，都忽略了材料基體變形對微凸體變形的影響。而在真實的接觸過程中，粗糙表面的基體和其上的微凸體都會產生形變，基體的變形對微凸體的接觸剛度計算有不可忽視的影響。只有將二者結合起來分析，才能得到更加準確的接觸剛度。在今后的研究中，如何將微凸體變形反映在接觸剛度模型中是一個重要的研究方向。

（3）考慮微觀接觸的宏觀接觸有限元模型。由于結合面接觸剛度解析計算存在大量的簡化過程，其計算結果與實際接觸狀態有很大差異，因此建立完整的粗糙結合面實體模型具有重要意義。隨著計算機技術水平的不斷提高，應用有限元方法建立的微觀粗糙表面接觸模型已經成為一種趨勢。但受計算能力的限制，很難將整個粗糙面的接觸狀態表征到宏觀模型上。如何將微觀接觸力學性能反映到宏觀接觸有限元模型中，也是將來的主要研究方向。

6 結束語

接觸剛度一直是影響航空發動機結構穩定性與可靠性的重要參數之一。基于統計學描述的接觸剛度計算模型雖日漸成熟與完善，但仍有許多不足之處。學者提出的分形模型可通過分形參數定量地表達總的接觸剛度與粗糙度的關系，但并非所有的粗糙表面都具有分形特征。基于納米級粗糙表面接觸剛度模型、考慮基體變形的粗糙表面接觸剛度模型、考慮微觀接觸的宏觀接觸有限元模型可彌補解析模型的不足，將是接觸剛度計算模型的未來發展方向。