彈性機翼剛度的靜氣彈敏感性研究

陳愷，劉曉燕，程攀，毛昆

上海飛機設計研究院，上海 201210

0 引 言

現代大型民用客機為追求經濟性和燃油效率，提高市場競爭力，多遵循高馬赫巡航、低結構重量[1]的設計理念，機翼結構多采用復合材料，不可避免地導致了機翼柔度增大[2]、彎曲和扭轉變形加劇、機翼載荷分布改變。飛機氣動性能降低甚至操縱面出現反效及靜氣動彈性（簡稱“靜氣彈”）效應已經成為影響飛機飛行性能、安全性等指標的重要原因[3-4]。

經過風洞試驗驗證的在設計巡航點具有最佳氣動性能的外形為巡航設計外形；在機翼設計過程中消除機翼靜氣彈變形影響后形成的用于生產制造的地面外形即為型架外形[5]；型架外形在實際高空飛行時承受氣動載荷、慣性載荷等作用后成為彈性外形[6]。

進行靜氣彈評估時，機翼結構剛度是確定機翼結構變形對飛機氣動特性影響的重要因素[7]。國內外學者針對大展弦比機翼的剛度設計與靜氣彈評估開展了研究。Bisplinghof等[8]將機翼簡化為沿機翼剛軸方向的懸臂梁，并引入剛度影響系數進行剛度設計；Schuster[9]采用多項式函數模擬剛度曲線，可在已知機翼載荷和扭轉分布的情況下反推機翼剛度；劉東岳等[10]提出基于梁架模型氣動彈性優化方法和三維優化模型折算方法來進行機翼總體剛度設計；張建剛等[11]耦合工程梁理論和升力面理論來評估機翼彈性對氣動載荷的影響。傳統方法多采用簡化的氣動和結構工程模型，靜氣彈評估精度有所降低。如何耦合高效率、高精度的氣動彈性分析方法是評估彈性機翼剛度靜氣彈影響的一個核心問題。

本文以某大展弦比后掠翼為研究對象，耦合基于 RANS（Reynolds Averaged Navier–Stokes）方程的 CFD（Computation Fluid Dynamics）求解器和結構靜力學求解器，發展型架外形設計方法，圍繞彈性機翼的剛度開展靜氣彈敏感性研究，包括分析機翼型架設計的魯棒性、建立機翼剛度與全機氣動導數預測模型以及分析機翼剛度優化敏度。

1 理論方法

1.1 流固耦合方法及型架外形設計方法

本文通過耦合定常Navier–Stokes方程[12]求解器和有限元分析方法，建立流固耦合分析方法，提出基于巡航外形的型架外形設計方法，并基于型架外形開展流固耦合靜氣彈分析。流體計算采用貼體結構網格，如圖1所示。以k–ωSST湍流模型實現流體方程的封閉[13]，對流項離散采用二階迎風格式，并采用多重網格技術加速流場壓力分布的收斂。

圖1 流體網格Fig.1 Fluid grid

結構分析基于反映結構變形和載荷關系的結構靜平衡方程。由于其他部件（包括機身、尾翼、發動機及吊掛）均為剛體部件，雖然發動機、吊掛會隨機翼彈性變形產生位移，但與機翼的相對位置始終保持不變，因此本文僅考慮機翼部件的彈性變形。采用如圖2所示的魚骨模型建立結構模型。

圖2 結構模型Fig.2 Structural model

結構網格點的位移及氣動網格點的氣動力數據傳遞采用無限平板插值方法[14]。為了避免大量網格點移動導致交叉點和網格負體積增多，采用基于非結構背景網格的彈簧網絡動網格技術[15]實現流場網格的變形。本文的型架外形修正方法既能反映三維流場的真實流動，也能反映因結構彈性變形導致的機翼展向典型翼型剖面的扭轉角分布。型架設計流程如圖3所示。

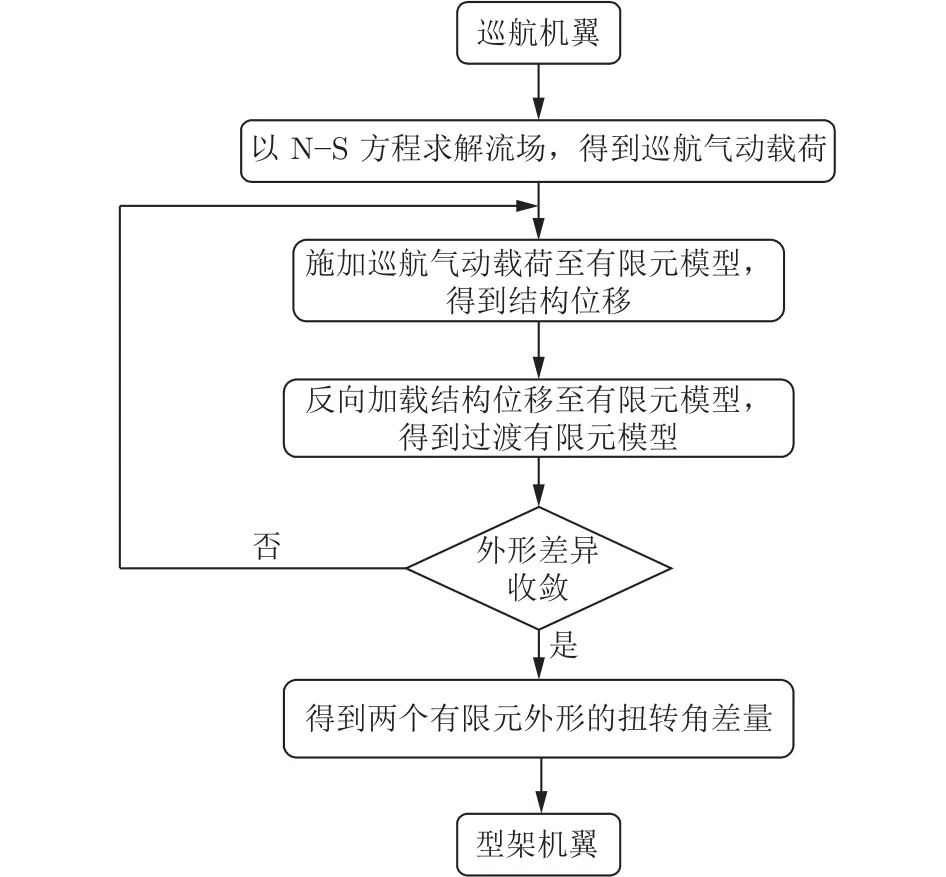
圖3 型架外形設計流程Fig.3 Jig shape design process

本文將 CRM（Common Research Model）模型作為驗證模型。耦合計算得到的升力系數（CL）、俯仰力矩系數（Cm）與風洞試驗結果[16]的對比分別如圖4、5所示，圖中橫坐標為迎角α，升力系數曲線、俯仰力矩系數曲線均與試驗結果保持“平行”，驗證了本文CFD/CSD方法的精度。

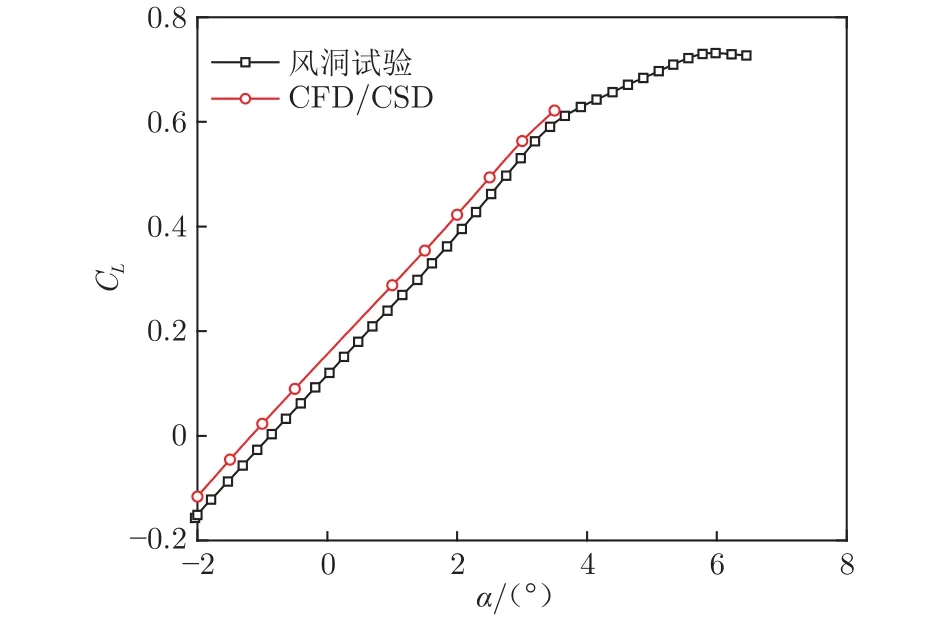
圖4 升力系數曲線Fig.4 Lift coefficient curve

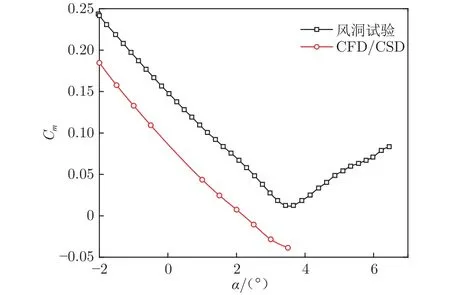
圖5 俯仰力矩系數曲線Fig.5 Pitch moment coefficient curve

1.2 設計敏度分析方法

在進行優化設計時，獲取設計敏度信息可以提高優化效率，減小設計變量定義的不同對優化結果的影響[17-18]。約束函數相對于某設計變量的敏度越大，該設計變量的變化對函數的影響越大，則該設計變量的重要程度越高。同一函數相對于不同設計變量的重要程度是不同的；對于不同的函數，同一設計變量的重要程度也是不一樣的。設計敏度的重要性評估公式[19]為：

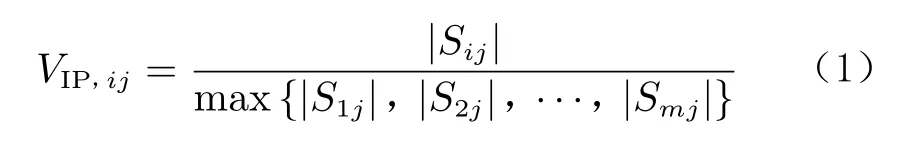
式中，VIP，ij為第i個設計變量相對于第j個函數的重要性， Sij為第j個函數相對于第i個設計變量的設計敏度，m為設計變量的個數。單個設計變量的敏度系數在整體敏度中所占的百分比貢獻計算公式為：

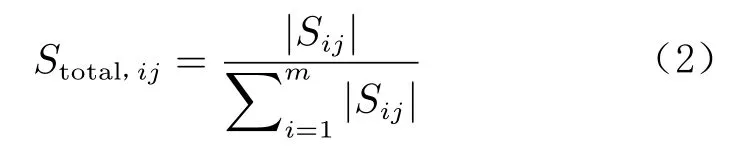
一組同類型的設計變量敏度系數在整體敏度中所占的百分比貢獻計算公式為：

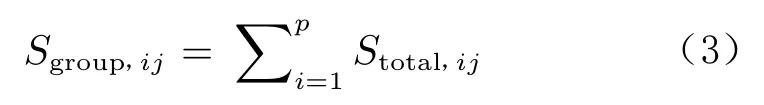
式中，p為同類型設計變量個數。

本文選取機翼肋站位的剛心點的梁特性作為設計變量，包括垂直彎曲剛度、面內彎曲剛度和扭轉剛度，約束選取翼尖扭轉角及升力效率，利用Nastran軟件開展靜氣彈約束的設計變量敏度分析。

2 剛度對機翼型架外形設計的敏感性分析

在飛機詳細設計階段的中后期，巡航設計機翼外形凍結，但機翼的剛度特性仍然處于多輪迭代中。為了縮短研制周期，凍結型架外形具有重要的實際工程意義。

以大展弦比跨聲速后掠翼為研究對象，改變機翼剛度，剛度比分別為 0.8、0.9、1.0、1.1、1.2。將剛度比為1.0時的設計型架外形定義為凍結型架外形，在其他剛度比下根據新剛度特性更新有限元模型。比較分別從新設計型架外形、凍結型架外形出發，經過流固耦合計算變形得到彈性外形的扭轉角差量，搜索凍結型架外形的臨界剛度比。

巡航馬赫數為0.84，采用定升力計算以保持飛機始終處于相同飛行狀態下，巡航升力系數為0.49。圖6為不同剛度比下是否進行型架外形設計的彈性機翼扭轉角差量（ Δθ）展向分布對比，其中 Δθ的表達式為：

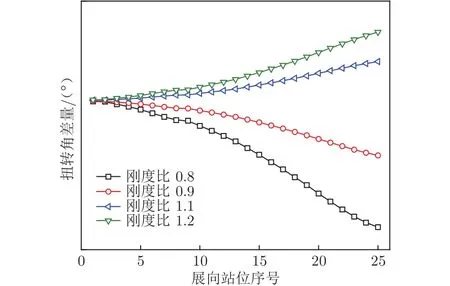
圖6 彈性機翼的扭轉角差量Fig.6 Delta twist angle of elastic wing along wing span

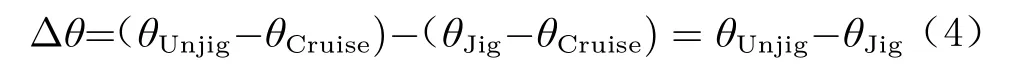
式中，θUnjig為從凍結型架外形出發得到的彈性機翼扭轉角，θJig為從新設計型架外形出發得到的彈性機翼扭轉角，θCruise為巡航設計外形的扭轉角。

圖7為彈性機翼的翼尖扭轉角差量與剛度比的關系。 Δθ與剛度比并非線性關系，剛度的增大和減小對扭轉角的影響并不對稱，減小剛度對扭轉角的影響更為顯著。機翼剛度變化越大，|Δθ|越大，且機翼剛度減小比剛度增大導致的扭轉角變化更為明顯，更新型架外形尤為必要。當剛度增大且剛度比不高于1.1時，扭轉角誤差低于風洞試驗測量的角度誤差，這意味著精度在工程設計可接受范圍內。

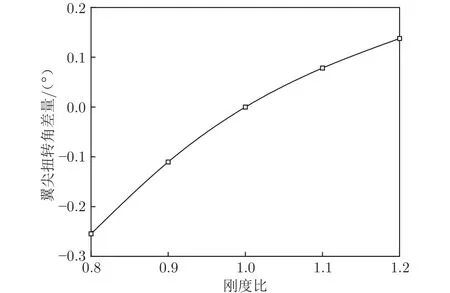
圖7 彈性機翼的翼尖扭轉角差量與剛度比的關系Fig.7 Relationship between delta wing-tip twist angle and stiffness ratio

圖8為不同剛度比（1.1、1.2）下，3種機翼構型在展向85%站位處的壓力分布對比。圖中，Cruise為巡航設計外形，Unjig為從凍結型架外形出發變形得到的彈性外形，Jig為從新設計型架外形出發變形得到的彈性外形，縱坐標為壓力系數Cp，橫坐標為弦向相對位置x/c。圖中剛度比為1.1時，3條曲線重合度較高，壓力分布差異不大，但剛度比增大到1.2時，Unjig在壓力面靠近前緣處與另外兩條曲線有一定差異，且Unjig的激波弦向位置更接近后緣，Jig的壓力分布更接近Cruise。

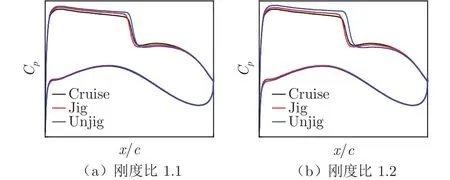
圖8 壓力分布對比Fig.8 Comparison of pressure distribution

剛度比不同時，是否進行型架修正，巡航點處全機氣動力系數差異有所不同。剛度比為1.1時，同升力時巡航迎角差量≤0.1°，阻力差量≤0.000 1，翼根彎矩差量≤1%；但剛度比為1.2時，全機氣動特性對型架外形較為敏感，巡航迎角、阻力特性及載荷特性差異明顯增大。

綜合考慮扭轉角分布、壓力分布及全機氣動特性，在飛機工程設計的后期，當機翼結構剛度變化≤10%時，為了節省資源、縮短研制周期，可從工程設計角度出發凍結型架外形，評估剛度變化引起的彈性影響。

3 基于機翼剛度的全機彈性氣動特性模型

根據第2節的結論，在剛度變化≤10%時，為簡化設計流程，節約資源成本，采用凍結外形。剛度變化＞10%時，利用更新剛度的有限元模型重新進行型架外形設計，并通過流固耦合方法得到彈性外形，建立機翼剛度比（1.04、1.08、1.10、1.20）與全機氣動特性的函數關系，并采用剛度比為1.06的算例檢驗預測模型的準確度。

將剛度比為1.00的氣動導數作為基準值，建立全機升力系數曲線斜率、全機俯仰力矩系數曲線斜率的差量百分比與剛度比之間的關系，分別如圖9、10所示。由圖可見，升力系數曲線斜率及全機俯仰力矩系數曲線斜率與剛度比均呈現良好的線性關系。

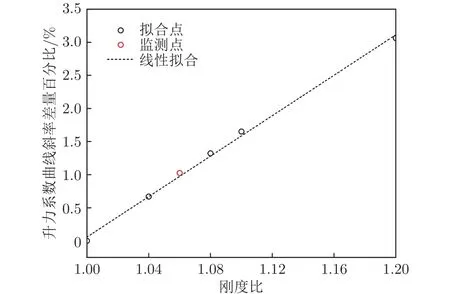
圖9 升力系數曲線斜率與剛度比的關系Fig.9 Relationship between slope of lift curve and stiffness

升力系數曲線斜率差量百分比與剛度比的函數模型如式（5）所示：

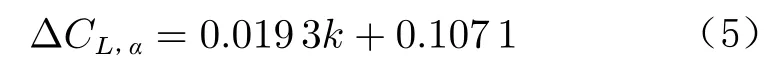
式中，CL，α為升力系數曲線斜率，k為剛度比。俯仰力矩系數曲線斜率差量百分比與剛度比的函數模型如式（6）所示：

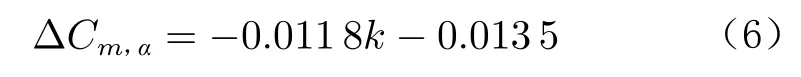
式中，Cm，α為俯仰力矩系數曲線斜率。

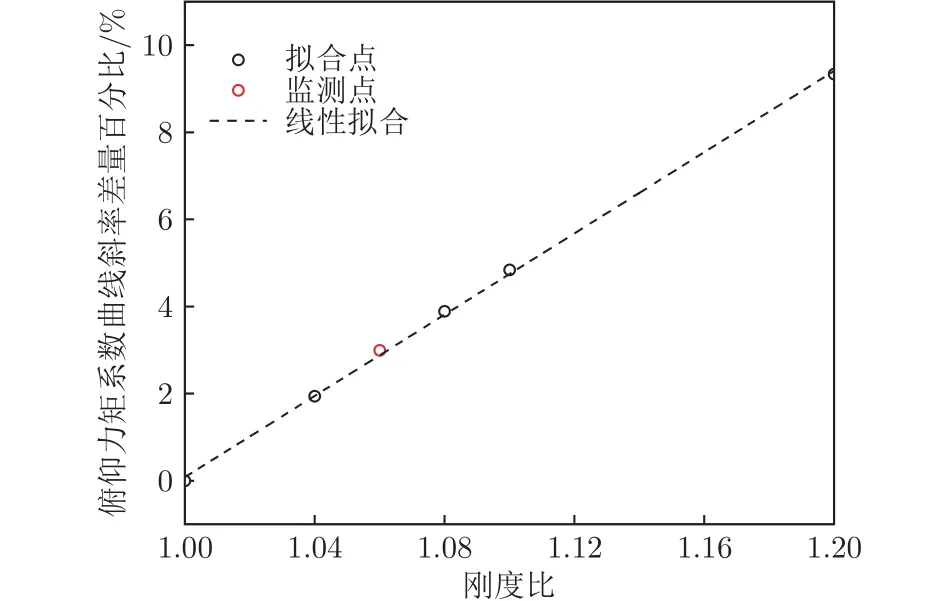
圖10 俯仰力矩系數曲線斜率與剛度比的關系Fig.10 Relationship between slope of pitching moment curve and stiffness

當剛度比為1.06時，流固耦合方法所得的彈性氣動導數與函數模型預測的結果吻合較好。當機翼剛度頻繁迭代時，可以基于此線性工程模型，快速評估彈性氣動導數與剛度比之間的關系，無需重新建立耦合模型進行仿真模擬。

4 機翼剛度敏度分析

垂直彎曲剛度、面內彎曲剛度及扭轉剛度在扭轉角、升力效率約束中的分布分別如圖11、12所示。升力效率為彈性升力系數曲線斜率與剛性升力系數曲線斜率的比值。由圖可見，垂直彎曲剛度、扭轉剛度是影響此兩種約束的主要設計變量。

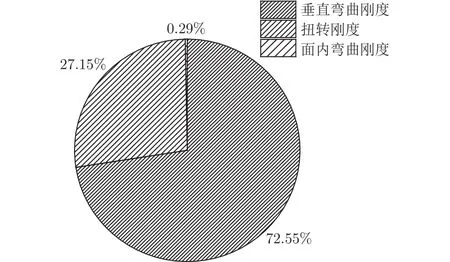
圖11 剛度特性在扭轉角約束中的分布Fig.11 Distribution of stiffness characteristics under the constraint of twist angle

垂直彎曲剛度對扭轉角、升力效率的設計敏度重要性分別如圖13、14所示，橫坐標表示垂直彎曲剛度設計變量，編號排序從小到大表示從翼根到翼尖的梁展向站位，翼尖站位的垂直彎曲剛度對扭轉角影響較為顯著，翼根站位的垂直彎曲剛度對升力效率影響較大。扭轉剛度對扭轉角、升力效率的設計敏度重要性如圖15、16所示，扭轉剛度對扭轉角的影響明顯集中在翼尖站位，而翼根站位的扭轉剛度對升力效率影響顯著。

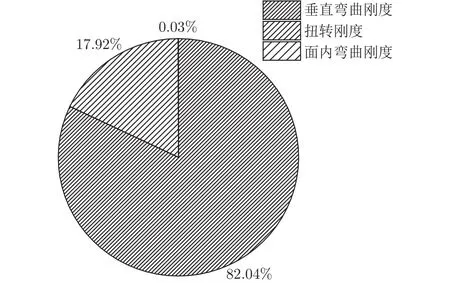
圖12 剛度特性在升力效率約束中的分布Fig.12 Distribution of stiffness characteristics under the constraint of lift efficiency

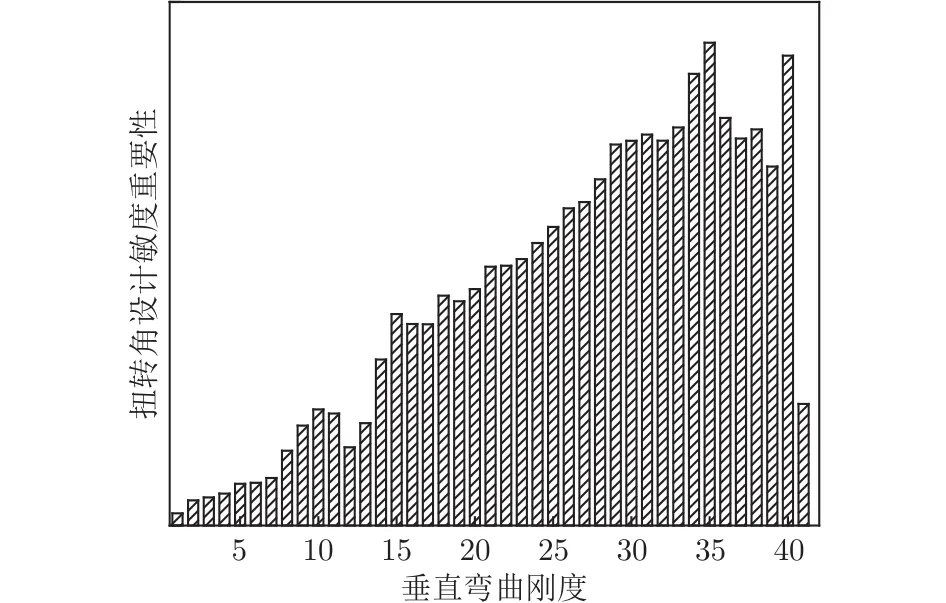
圖13 垂直彎曲剛度對扭轉角的設計敏度重要性Fig.13 Design sensitivity importance of vertical bending stiffness to twist angle

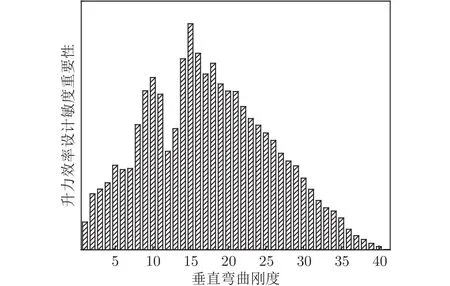
圖14 垂直彎曲剛度對升力效率的設計敏度重要性Fig.14 Design sensitivity importance of vertical bending stiffness to lift efficiency

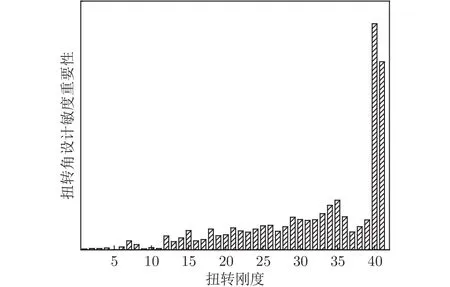
圖15 扭轉剛度對扭轉角的設計敏度重要性Fig.15 Design sensitivity importance of torsional stiffness to twist angle

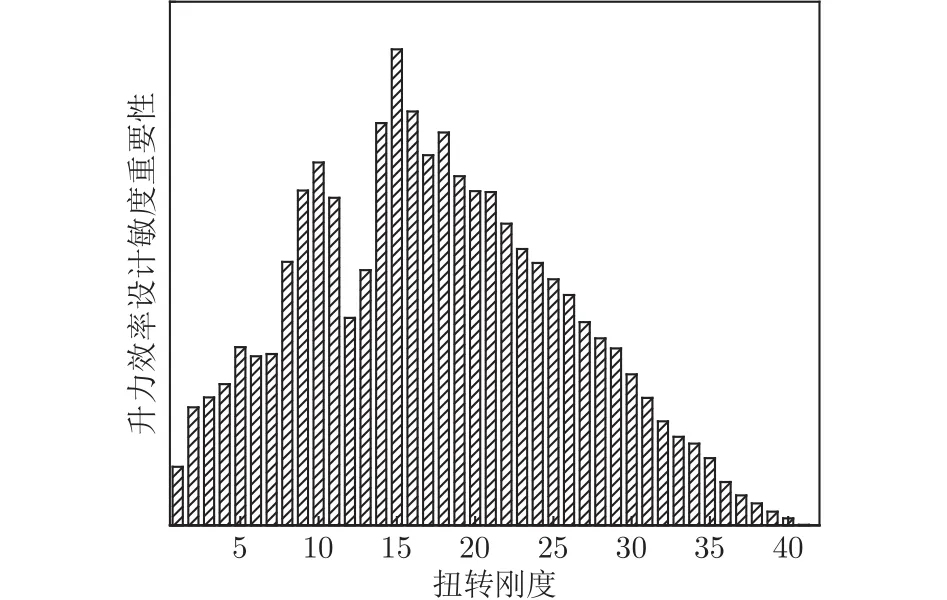
圖16 扭轉剛度對升力效率的設計敏度重要性Fig.16 Design sensitivity importance of torsional stiffness to lift efficiency

通過敏度分析，可以搜索展向各站位分區的剛度特性對機翼靜氣彈效應的影響程度，為機翼剛度設計縮小優化范圍，提供局部優化方向，以控制氣動升力面的靜態彈性變形，提高優化設計效率。

5 結 論

本文發展了流固耦合分析及型架外形設計方法，針對某大型客機彈性機翼開展剛度靜氣彈敏感性研究，可為型號設計中的靜氣彈快速評估提供工程支持，主要結論如下：

1）綜合考慮扭角分布、壓力分布及全機氣動特性，當機翼結構剛度變化≤10%時，可凍結型架外形，縮短研制周期。

2）全機升力系數曲線斜率、全機俯仰力矩系數曲線斜率與剛度比呈線性關系，基于此規律建立工程快速預測模型，當僅更新剛度值時，可快速評估彈性氣動導數。

3）垂直彎曲剛度、扭轉剛度是影響扭轉角及升力效率的主要設計變量，翼尖站位的垂直彎曲剛度及扭轉剛度對扭轉角的影響明顯，翼根站位的垂直彎曲剛度及扭轉剛度對升力效率影響明顯。