重建思維過程，發展數學能力
——“正余弦定理”教學中滲透數學方法

◎曾春燕 （廣東茂名幼兒師范專科學校理學院，廣東 茂名 525200）

一、挖掘蘊含的數學思想方法

高中數學課程標準指出：“在教學中，教師應結合相應的教學內容，落實‘四基’，培養‘四能’，促進學生數學核心素養的形成與發展．”這里面強調的“四基”就包括數學的基本思想方法．數學思想方法是數學學科的精髓，是數學素養的重要內容之一．學生只有領悟了數學思想方法，才能有效地應用知識，形成能力，養成思考問題的習慣．

數學發展的過程就是從實踐中發現問題，探究解決問題的思想方法，從而提煉、概括、抽象出數學概念、定理、法則等．高中數學課本呈現的是以概念、定理、法則、公式等為元素的嚴謹的邏輯體系．教師在教學過程中不應只重視知識的講解與傳授，還應有重建思想方法的過程，展示數學知識的發生發展過程，讓學生能體驗到數學思想方法的意義和作用．

我們本著這樣的理念來重新設計“正余弦定理”的教學，深入挖掘這節課蘊含的數學思想方法，從而發現這節課包含了特殊到一般、數形結合以及化歸的思想方法．具體設計思路如圖1：

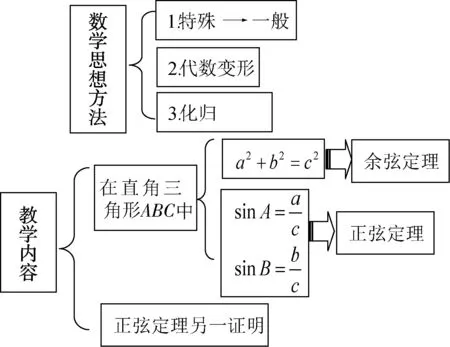
圖1

二、重建數學思想的教學過程

（一）知識到方法，提供思想方法模型

數學的新知識產生的方式有兩種．一種是以實際為起點．另一種是以已有的數學為起點，即由已有的數學理論推理出新的數學理論．前者運用的是歸納法，后者運用的是邏輯推理．

1．數學的產生

教師提問：數學的新知識怎么來？

隨后教師給學生介紹數學新知識的來源：

（1）產生于實際，即以實際例子為起點，通過歸納得出相關的數學知識；

（2）產生于已有的數學知識，即通過用已有的數學知識推理出新的數學知識．

第二種方式是高中生要掌握的主要方式．

2．推理的方法

用已有的數學知識推理出新的數學知識，推理的方法主要有：

（1）特殊與一般；

（2）代數變形；

（3）化歸思想．

（設計意圖：一般地，當人們明確了學習某一知識的目的性和必要性以后，學習這一知識的熱情必將得到極大的提高．然而，如何探究一般三角形中邊角關系？ 學生大多缺乏明確的思想認識和有效的思維方法．教師向學生介紹數學思維的方法，有利于激發學生的興趣和學習的欲望．）

（二）公式到問題，指引新知產生路徑

三角形的邊角關系是三角形中最重要的關系之一，而余弦定理和正弦定理是刻畫三角形邊角關系最為重要的兩個定理，它們為解三角形提供了基本而重要的工具．為了更好地體現向量的價值，教科書用向量方法推導了余弦定理和正弦定理，但是這樣容易掩蓋數學知識產生的過程性．為了讓學生更好地體驗數學知識產生的過程與數學思想方法的聯系，教師可以利用已經學生學習過的勾股定理引導學生進行思考．具體設計如下：

1．回憶勾股定理

引導學生回憶勾股定理：在直角三角形ABC中，有a2＋b2＝c2．教師要引導學生明確這個公式成立的前提是在直角三角形中．

2．指引可思考的方向

教師提問：對這個結論，你有什么想法？

教師引導學生思考，概括出幾個思考的方向：

（1）這個公式是對直角三角形來說的，那么對于一般的三角形，三邊有什么關系？

（2）平方變成立方，有什么成立？

（3）滿足a2＋b2＝c2的數有哪些？

（4）能否推廣a2＋b2＋c2＝d2？ 甚至推廣到：四個以上數的平方和是一個完全平方數？

（設計意圖：通過學生熟悉的勾股定理，引導學生對已有的數學知識進行更加深層次的思考，從而拓展學生的思維，豐富學生的認識，同時為新的數學知識的產生做鋪墊．）

（二）特殊到一般，發現余弦定理的部分內容

上面思考的四個方向中的（1）是從特殊到一般的方法．學生在理解勾股定理反映的是直角三角形三邊的關系后，提出一般三角形的三邊具有的關系．

1．分類討論

問題1：在銳角三角形ABC（如圖2）中，三邊有什么樣的關系？

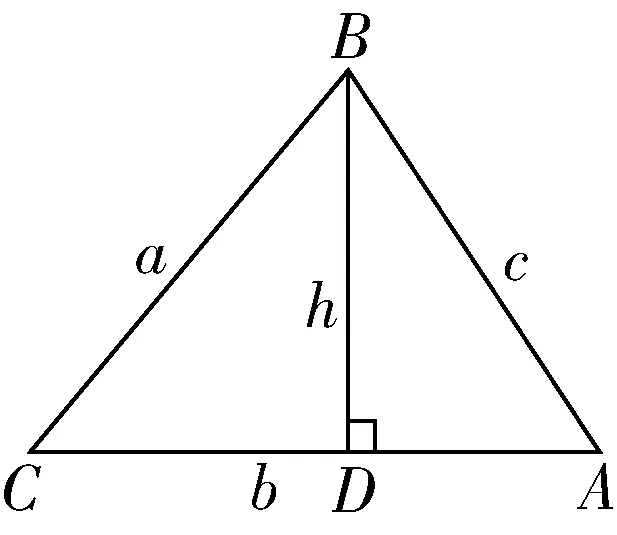
圖2

分析：可以考慮將其化歸為直角三角形．因此可作高BD．

解過頂點B作邊AC上的高BD交于AC于D．于是有：

c2＝h2＋AD2

＝h2＋（b-CD）2

＝h2＋b2-2b·CD＋CD2

＝（h2＋CD2）＋b2-2b·CD

＝a2＋b2-2b·CD

＝a2＋b2-2ab·cosC

問題2：在鈍角三角形ABC中，三邊有什么樣的關系？

（證明與問題1 相同，故省略．）

2．余弦定理

結合上面的證明，我們得到余弦定理：在三角形ABC中，c2＝a2＋b2-2ab·cosC．由此可知，余弦定理是勾股定理的推廣，勾股定理是余弦定理的特例．

3．拓展思考

教師提問：在三棱錐里，棱長之間有什么關系？ （課外完成）

（設計意圖：使用“斜三角形轉化成兩個直角三角形”這種從一般向特殊、由未知向已知轉化的數學思想解決問題，有助于培養學生的思維能力．）

（三）舉一到反三，完善余弦定理的全部公式

代數變形是利用代數知識實施形變而質不變的一種變形，即將一個問題等價地變換為另一個問題，由一種形式轉換為實質等價的另一種形式．余弦定理是由若干條公式組成的．通過上面的環節，我們得到了“在三角形ABC中，c2＝a2＋b2-2ab·cosC”，那么如何得到其他的公式呢？ 此時我們可以使用類比和代數變形來實現．具體如下：

1．類比寫式子

教師提問：類似c2＝a2＋b2-2ab·cosC的式子可以寫多少個？ 請通過結合圖形觀察c2＝a2＋b2-2ab·cosC的規律，嘗試寫出．

總結：

在三角形ABC中：（1）c2＝a2＋b2-2ab·cosC；

（2）a2＝b2＋c2-2bc·cosA；

（3）b2＝a2＋c2-2ac·cosB．

上面這個式子體現了余弦定理中的邊a，b，c可以進行輪換，即可以從余弦定理的一個式子得到其余的兩個式子．因為余弦定理中的邊具有可輪換的特點，所以余弦定理可以用概括性的文字語言統一敘述，即教科書中給出的文字敘述．教學中教師可以引導學生自行用文字語言敘述余弦定理，以此培養學生的數學表達能力．

2．代數變形

余弦定理的推論指出了三角形的三條邊與其中的一個角之間的關系，并且每一個等式中都含有四個不同的量，即三角形的三條邊和一個角．不難看出，若已知其中的三個量，我們就可以求出第四個量．用三角形的三條邊表示角的余弦，即可獲得余弦定理的推論，有時也說成是余弦定理的第二種形式：

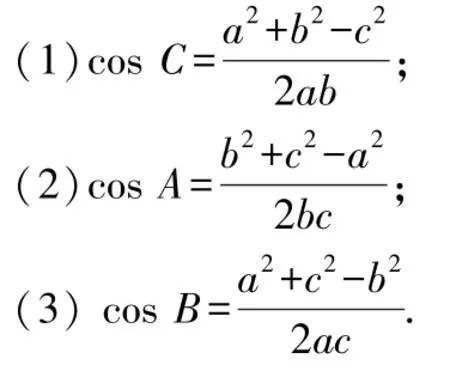
教師提問：已知三角形的三邊，能否算出三個內角的度數？ 這時我們應該思考的是在某種情況下三角形哪些要素能算，哪些要素不能算．

（設計意圖：引導學生通過類比猜想得出余弦定理的另外兩條公式，培養學生的合情推理能力．對余弦定理運用代數變形，有助于加深學生對余弦定理的理解．）

（四）特殊到一般，發現特殊情況下的正弦定理

教師提問：既然有余弦定理，會不會也有正弦定理？

直角三角形ABC中，有：

回顧：

剛才我們得出余弦定理時用到了的思想方法：（1）從特殊到一般的方法；（2）代數變形．

思考：①式對一般的三角形成立嗎？

（設計意圖：通過對學生熟悉的正弦函數的定義進行代數變形，“從特殊到一般”提出正弦定理的普遍性，有利于訓練學生從特殊情況提出一般性結論的思維能力．）

（五）化歸與推理，探究一般情況下的正弦定理

分析：可以考慮將其化歸為直角三角形．因此可作高BD（如圖3）．

圖3

解過頂點B作邊AC上的高BD交于AC于D．于是有：

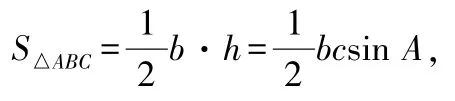
教師提問：我們要得到的是①式，此時你們有什么想法？ （代數變形）

教師提問：如果我們說，對于一般的三角形，有②式成立，對不對？ 你們對此有什么想法？

（設計意圖：再次使用“斜三角形轉化成兩個直角三角形”這種從一般向特殊、由未知向已知轉化的數學思想來解決問題，有助于培養學生的思維能力．通過引導學生思考為什么要把②式倒過來變成①式，讓學生體驗到數學公式的嚴謹性和美觀性．）

（六）探幽與入微，深化理解正弦定理

分析：

由②式想到：（1）比值不變；（2）已知A與a，比值就定下來了．

①角A定，邊a變，但比值不變．

此時，a邊的長度不變，但是a邊的位置是可以無法確定的（如圖4），觀察a邊的軌跡是不規則的．

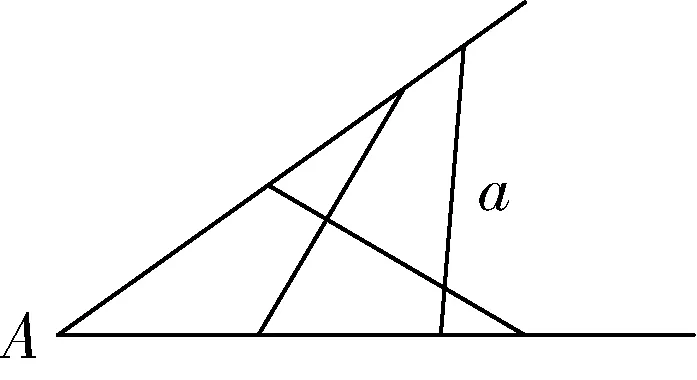
圖4

②邊a定，角A變，但比值不變．

a邊所對的角A大小是不變的，但是位置可變，根據圖形的分析，我們可以由同弧所對的圓周角相等想到角A的軌跡是a邊為弦的圓．

找一種特殊的情況，角A的一邊過圓心（如圖5、圖6）．

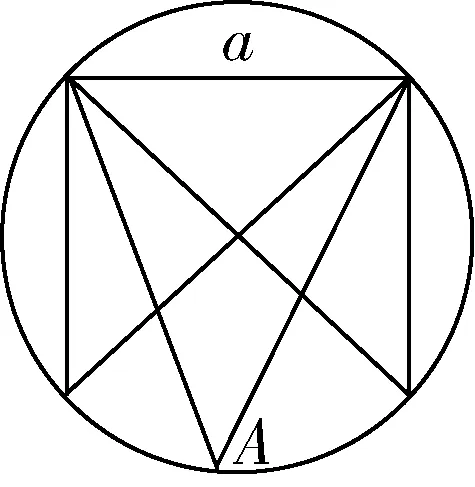
圖5

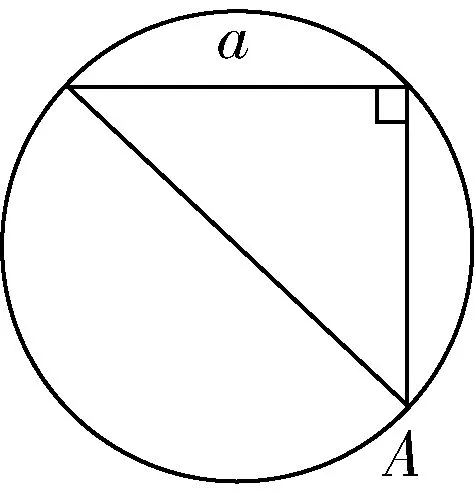
圖6

因此，要將②式倒過來寫：

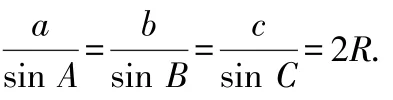
這道題我們用到了：代數變形和數形結合的方法．

正弦定理，常用可寫成：

a＝2RsinA；

b＝2RsinB；

c＝2RsinC．

教師提問：從中你能發現什么？

推論：在△ABC中，A＞B?a＞b．

簡證：A＞B?sinA＞sinB?2RsinA＞2RsinB?a＞b．

（設計意圖：通過分析角A與邊a的幾何關系得出正弦定理中的定值的幾何意義，學生體會到代數與幾何的密切聯系．學生在分析討論中再次體會到代數變形和數形結合的方法的重要性．）

（七）構造與創新，用向量的方法推導正弦定理

教師提問：你還有其他方法推導正弦定理嗎？ （向量法）

解作AB的法向量i（如圖7），

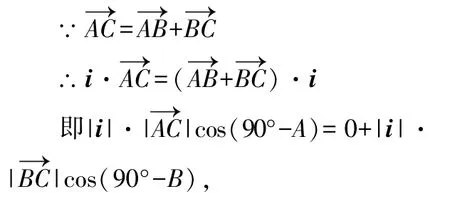
圖7

因此有bsinA＝asinB，即

（設計意圖：用向量的方法推導正弦定理，讓學生認識到數學知識是相互聯系的．）

（八）應用與轉化，用正余弦定理解決實際問題

實際問題：某林場為了及時發現火情，設立了兩個觀測點A和B．某日兩個觀測點的林場人員都觀測到C處出現火情．在A處觀測到的火情發生在北偏西40°方向，而在B處觀測到火情在北偏西60°方向．已知B在A的正東方向10 km處，要確定火場C分別距A及B多遠．

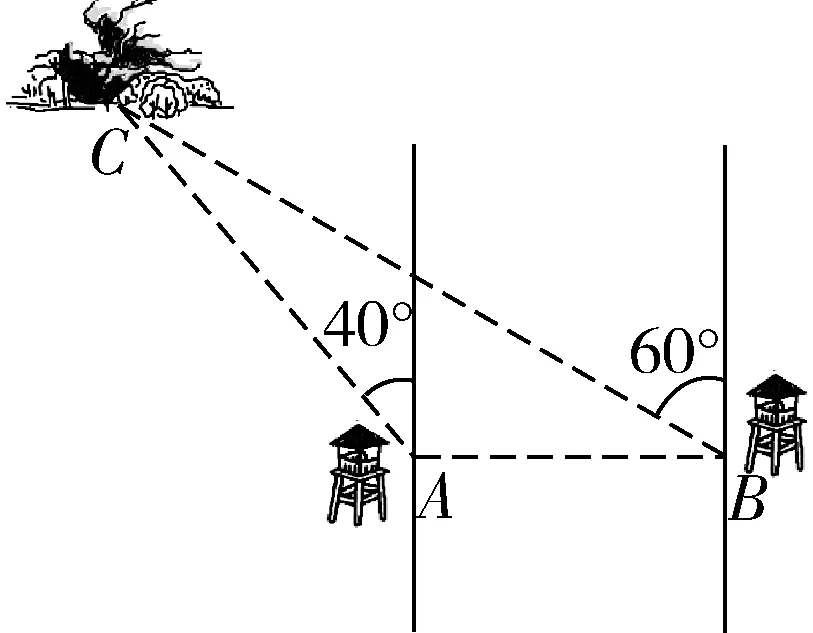
圖8

數學問題：如圖，在△ABC中，已知 ∠CAB＝ 130°，∠CBA＝30°，AB＝10 km．求AC與BC的長．（結果精確到0．1 km）

（設計意圖：從實際情境出發，引導學生將實際問題轉化為數學問題，培養學生數學建模素養．利用正弦定理解決課前的引例，體現了正弦定理在實際生活中的應用，進一步反映了學習正弦定理的必要性．）

三、總結

挖掘教學內容中所蘊含的數學思想，有助于發展學生的數學能力．符合學生認知特點的過程性教學，將引導學生由“雙基”走向“四基”，由“兩能”走向“四能”，彰顯數學的特質和意味，促進學生數學素養的發展．