核心素養下數學猜想在數學教學中的應用

◎商鈺瑩 （張家港市合興初級中學，江蘇 張家港 215600）

教育是培養人的事業，教師是教育的主力軍，教學具有教育性，數學課堂教學不僅僅是計算和證明，還可以進行核心素養的滲透、思維能力的培養、解題方法的總結．隨著我國新課改的不斷推進，教學對學生核心素養的要求也越來越高．核心素養理念是培養學生思維能力的重要手段，數學教學改革要求數學教師站在核心素養的高度，將學生數學猜想能力的培養貫穿于數學教學中，由此引導學生數學核心素養的逐步養成和數學思維的增強．數學猜想是數學發展的重要路徑，在教育快速發展的今天，每一個數學理論和分支的產生和發展都烙上了數學猜想的烙印．數學猜想對一些數學理論的證明有著重要的意義．

一、數學猜想的定義及其特征

數學猜想以數學知識和數學事實為基礎．數學猜想如果被驗證真實存在，就會轉化為數學定理，成為數學理論體系的重要組成部分，數學猜想不僅有利于數學理論的發展，還有利于數學方法論的研究．

邏輯和非邏輯兩部分構成數學猜想，所以教學猜想是科學的，人們通過推理和論證過程，確定猜想的正確性．推理和論證過程則是一種創造性的思維活動，有利于發展學生的思維能力．

二、核心素養下數學猜想的指導作用

核心素養背景下，教師應引導學生學會構建數學知識體系，為學生設計符合他們認知水平的學習過程．教師要懂猜想、會猜想，才能培養出具有猜想能力的學生，教師應在教學過程中注重學生數學思維、解題方法的培養．

要使學生掌握解題方法，教師就必須引導學生“再創造”．數學家已經對知識進行了論證和研究，學生要想發現規律，需要教師的指點和幫助．一般來說，猜想是新舊知識的融合，學生通過歸納、類比、觀察、聯想，得到最終的論證結果．

三、數學教學中的數學猜想

（一）歸納猜想

歸納猜想是解決數學問題的重要思維方法，歸納猜想就是按照一類事物的部分對象具備的某種性質，通過對問題的觀察、分析和討論，發現其內部具有的某種共性或規律，從而推出這類事物的一切對象都具有這種性質的一種推理．歸納猜想是從特殊到一般的過程．

例如，52＋122＝132，72＋242＝252，92＋402＝412，求第n個式子．

5、7、9 是連續的奇數，則猜想第n個式子中的第一位是2n＋1．12、13，24、25，40、41 是連續的兩個自然數，則設第二、三個數是分別k，k＋1．根據（2n＋1）2＋k2＝（k＋1）2，可得k＝2n2＋2n，所以第n個式子是（2n＋1）2＋（2n2＋2n）2＝（2n2＋2n＋1）2．

又如，算式2（3＋1）×（32＋1）×（34＋1）× …×（316＋1）＋1，求其個位數字．

此題主要考查了利用平方差公式探究規律．根據題中式子的特點，我們可以將2 寫成3-1，進行式子的簡化計算，得到：原式＝332，再根據3 的冪的特點，找出個位數字的規律，即可求值．原式＝（3-1）（3＋1）×（32＋1）×（34＋1）×…×（316＋1）＋1＝（32-1）×（32＋1）×（34＋1）×…×（316＋1）＋1＝（34-1）×（34＋1）×…×（316＋1）＋1＝332-1＋1＝332．

由31＝3，32＝9，33＝27，34＝81，35＝243，…，得到個位數是3、9、7、1 的循環，32÷4＝8，所以332的個位數是1．

近年來，越來越多的創新探究題出現在中考壓軸題中，通常涉及對圖形變化的歸納，對幾何圖形中數量關系的猜測探究，對位置關系及幾何形狀的猜測，這些都需要我們用心探索，掌握技巧．

如圖1，在△ABC中，∠A＝x°，A1是∠ABC與∠ACD的角平分線交點，A2是∠A1BC與∠A1CD的角平分線交點，A2022是∠A2021BC與∠A2021CD的角平分線交點，求∠A2022．

圖1

找出∠A1和∠A之間的規律是解題的關鍵．找出規律即可求出∠A2022．

因為BA1平分∠ABC，A1C平分∠ACD，所以∠A1CD＝

（二）類比猜想

類比是一種主觀的、不充分的、似是而非的推理，所以，為了證實猜想的有效性，我們要經過嚴密的邏輯論證．

學生在學習立體幾何時，可以類比平面幾何中的結論．如圖2，長方形與長方體類比，類比關系如下：

圖2

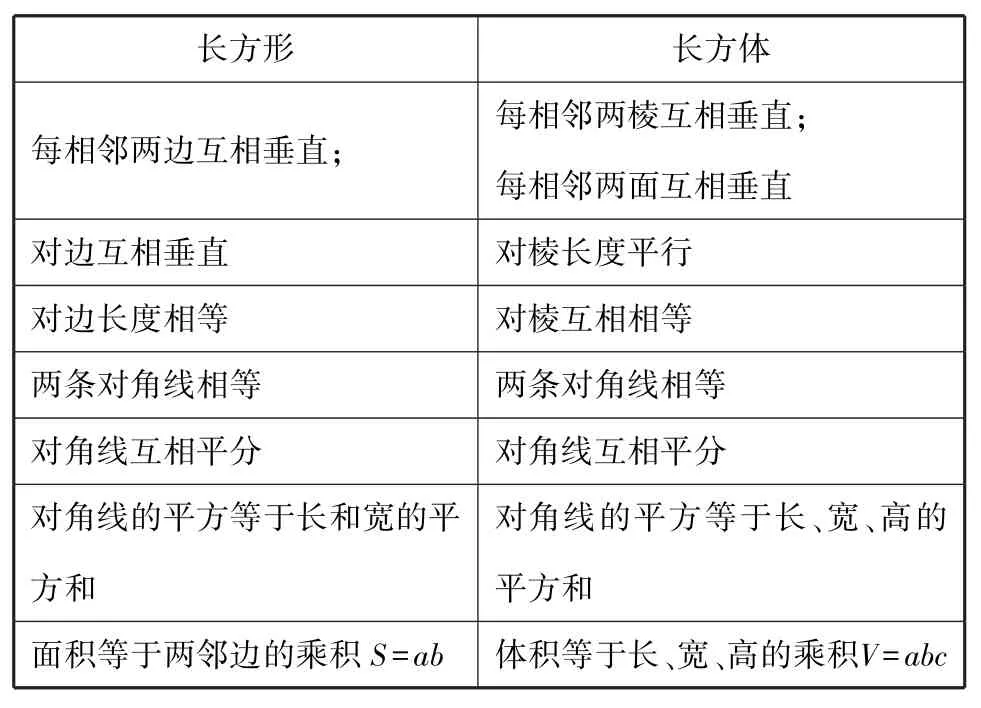
長方形長方體每相鄰兩邊互相垂直；每相鄰兩棱互相垂直；每相鄰兩面互相垂直對邊互相垂直對棱長度平行對邊長度相等對棱互相相等兩條對角線相等兩條對角線相等對角線互相平分對角線互相平分對角線的平方等于長和寬的平方和對角線的平方等于長、寬、高的平方和面積等于兩鄰邊的乘積S＝ab體積等于長、寬、高的乘積V＝abc

在學習相似三角形的性質時，可以類比全等三角形（如圖3）．類比關系如下表：

圖3

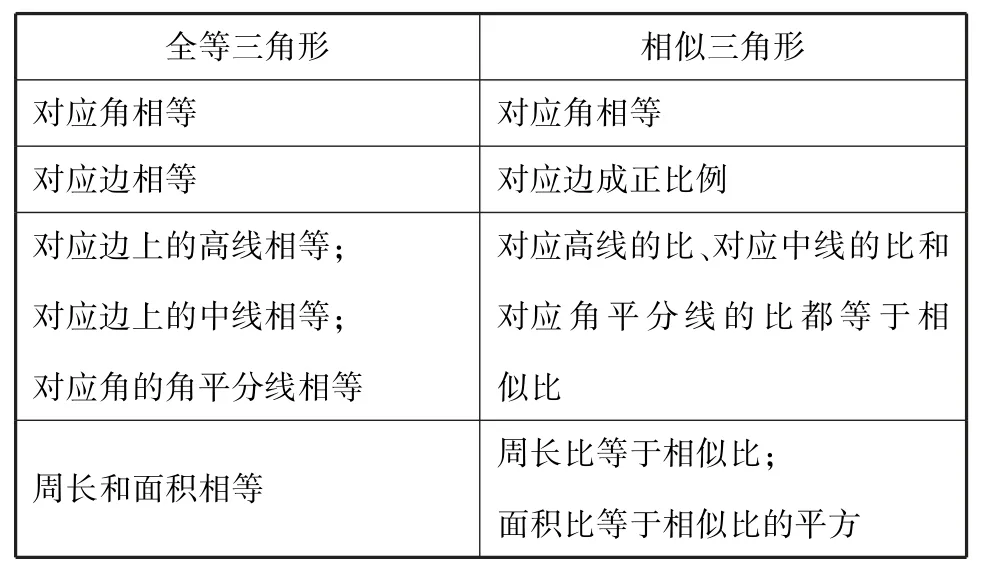
全等三角形相似三角形對應角相等對應角相等對應邊相等對應邊成正比例對應邊上的高線相等；對應邊上的中線相等；對應角的角平分線相等對應高線的比、對應中線的比和對應角平分線的比都等于相似比周長和面積相等周長比等于相似比；面積比等于相似比的平方

在求一元n次方程的根與系數之間的關系時，設ax2＋bx＋c＝0 的兩個根分別是x1，x2，則有ax2＋bx＋c＝a（x-x1）·（x-x2），整理得類比此方法，我們可以求出一元n次方程根與系數的關系．

設n次多項式f（x）＝anxn＋an-1xn-1＋…＋a1x＋a0的n個根為x1，x2，…，xn，則有anxn＋an-1xn-1＋…＋a1x＋a0＝an（xx1）·（x-x2）…（x-xn），整理得：

（三）觀察猜想

觀察猜想就是指導學生觀察和分析數學命題的結構、解題的過程，從而提出新的結論或論點．觀察猜想是發現問題和解決問題的重要途徑．中學生的抽象思維較弱，在幾何圖形教學過程中，學生可以通過觀察圖形的變換、轉化、運動、應用等過程，提升空間幾何感．

例如，41＝4，42＝16，43＝64，44＝256，45＝1024，46＝4096，…觀察等式，寫出4101的末位數字．

我們觀察以上等式，可以發現等式右邊數的末位數是4、6 這2 個數字的循環，由于101÷4＝25…1，所以4101的末位數字是4．

此題考查用代數式表示數量．我們仔細觀察分子和分母，易發現分子是從1 開始的奇數，分母是從3 開始的奇數．因此，第n個數應為形如2n-1 或2n＋1（n為正整數）的式子表示奇數．一般地，對于一個有規律排列的數列，當你探索出其中的規律并用含n的式子表示出第n個數之后，可以列舉數值代入表達式來證明猜想正確．

再如，若“！”是一種數學運算符號，并且：1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…求的值．

新定義題型是近年來的熱點問題，學生要讀懂題目，觀察其規律．因為100！＝100×99×98×97×…×1，98！＝98×97×…× 1，所以＝ 100 ×99＝9900．

在學習用配方法解一元二次方程時，觀察下列各式中常數與一次項系數之間的關系．

（1）x2＋6x＋32＝（x＋3）2；

（2）x2＋8x＋42＝（x＋4）2；

（3）x2-4x＋22＝（x-2）2；

（4）x2＋px＋（ ）2＝（x＋）2．

我們觀察等式的左邊，可以發現所填的常數是一次項系數一半的平方，通過觀察猜想，總結出一般規律x2＋px＋進而歸納出配方法的步驟．

（四）聯想猜想

聯想是類比的發展．教學過程中，我們通過聯想，可以將新舊知識串聯起來，有利于知識的發展與遷移，提高數學思維的靈敏性，從而完善學生的知識結構．

例如，學生學習了平行四邊形的性質后，可以通過聯想得到長方形、菱形和正方形的性質．在求不規則石塊的體積時，根據曹沖稱象的故事，我們可以利用規則的容器，求出水的體積，得出所求石塊的體積．

又如，已知tanα＝2，求sin2α-sinαcosα＋2 的值．

若根據tanα＝2 直接求正、余弦的值，則會出現取正負值的問題．我們應利用tanα＝2，求出的解，在式子中構造tanα．在解題時學生應注意式子中的分母問題，聯想到具有特殊性的式子sin2α＋cos2α＝1，即sin2α-

四、核心素養下數學猜想在數學教學中的意義

課堂是教學的主陣地，課堂教學是落實對學生核心素養培養的關鍵途徑．在中學數學教學中，教師需要為學生營造良好的課堂氛圍和學習環境，根據班級學生情況，因人施教，把學生放在課堂的主體位置，關注學生在課堂中的每一個眼神、每一個動作、每一次發言，以培養學生的數學核心素養為目標，結合現代教育理論，積極聯系學生的生活經驗和認知水平，探索并實踐培養學生猜想能力的有效途徑，幫助學生形成良好的數學學習思維，從而提升數學課堂的學習效率，促進學生的全面發展．

猜想對數學理論的建立和發展有著重要的作用．猜想是學生對知識信息進行構建的一種數學思維活動，具有一定的科學性和預測性．猜想過程不再是枯燥的填鴨式教學，通過讓學生先猜結果，再驗證是否正確，激發學生學習數學的興趣．長期進行猜想訓練，有利于提高學生的學習效率，從而促進學生核心素養的發展．在教學過程中，教師要注重培養學生的數學猜想能力，通過教師的引導，讓課堂教學更加符合學生的認知規律，從而落實對學生核心素養的培養目標．