爆破振動對高層框架-剪力墻結構的影響

李 猛，范延靜，李 彬，潘建榮，王 湛

(華南理工大學土木與交通學院，廣州 510641)

隨著爆破技術的廣泛應用，爆破施工帶來的危害也越來越受到關注[1]，特別是爆破地震波產生的爆破振動，它會對附近正在建或者已建成的建筑物產生損傷破壞[2-5]。因此，研究爆破地震波對建筑物的影響具有重要意義。

目前，關于爆破地震波的研究主要包括爆破振動傳播規律以及臨近建筑物的動力響應。對于爆破振動傳播規律的研究，前蘇聯學者M.A.薩道夫斯基通過對大量爆破數據進行分析，并結合相似原理，提出了薩道夫斯基公式，該公式在我國被廣泛應用于爆破振動分析[6]。然而，經典薩道夫斯基公式未考慮高程對振動速度的影響，使其應用范圍存在局限性。針對薩道夫斯基公式的不足，Marrara等[7],崔未偉等[8]對高程影響峰值速度進行研究，并指出峰值振動速度隨高差增加而增大。譚文輝[9]、郭得福等[10]通過量綱分析的方法，得到了考慮高程差的振速預測公式。隨著對爆破振動研究的深入，爆破地震波作用下建筑物的動態響應成為研究熱點之一。

雷振等[11]對爆破地震波作用下不同建筑高程振動規律進行探究，研究表明在測點同一樓層時，水平距離不變，隨著距地高差的增加，振動速度也越來越大。P.K.Singh等[12]研究不同起爆方式、爆破孔徑等相關爆破參數對結構的影響。羅藝等[13]，王松青等[14]，曹孝君[15]考慮了爆破地震波主頻對結構物的影響，研究表明振動速度的放大作用不僅與高程有關，還與爆破地震波主頻、振動傳播歷程等因素有關。但目前的研究集中于結構整體振動頻率與爆破地震波頻率的關系，而對于結構建筑內部構件振動速度局部放大效應研究存在不足。

本文結合廣東以色列理工學院二期校區山體爆破工程，采用爆破振動記錄儀對建筑周邊基礎和建筑結構內部進行監測。通過對振動數據進行線性回歸分析，確定結構內部振動頻率對結構局部振動放大效應的影響，從而探究爆破沖擊波的傳播規律以及爆破作用下高層建筑內部結構構件振動規律。通過研究建筑物振速與地基振速放大倍數的比值關系，可估計框架-剪力墻結構不同構件處振速，提出建筑結構中易破壞位置選取原則，對類似爆破工程安全施工起指導作用。

1 工程實例

1.1 工程概況

廣東以色列理工學院二期校區位于廣東省汕頭市金平區，校區南側山體存在大量土石方需要爆破。校區內教師宿舍BC棟臨近爆破山體，且施工工期與山體爆破時間相重合，為確保結構構件及施工安全，需要對結構關鍵構件采用施工監測。BC棟建筑為框架-剪力墻結構，高37.05 m，共12層。山體主要為燕山期花崗巖，采用延時起爆方式，相鄰藥包起爆時間間隔為75 ms。爆源單排布置，一排6個鉆孔，孔徑90 mm，孔深約8 m，孔距3 m，最大單段裝藥量144 kg，單孔藥量約24 kg。

1.2 測點布置

為研究爆破沖擊波振動傳播規律，采用JM-3874三向加速度傳感器對距離爆破點不同位置處地表振速進行監測。在此基礎上，為探究爆破對建筑結構內部構件的影響，根據建筑構件距爆破點距離的不同以及迎爆面的位置，采用JM-3874三向加速度傳感器對C棟建筑關鍵構件振速進行監測。

在距爆破點140、150、200、240、290 m處設置A～E共5個地表監測點(見圖1)，采用全站儀測量其x、y、z坐標。

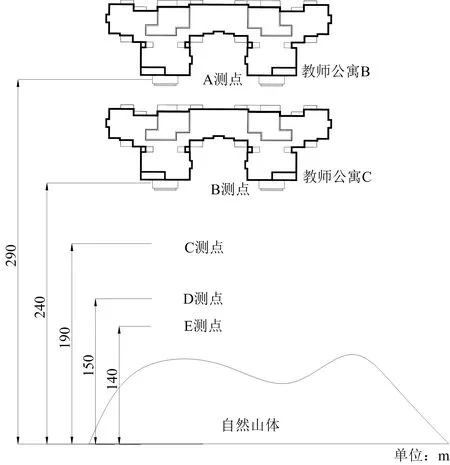
圖1 地表測點布置Fig.1 Layout of surface measuring points

C棟中測點布置如圖2所示，此時爆破點距C棟建筑水平距離為340 m。測點編號按照測點方位：W(西側)、E(東側)、C(中部)，結合測點前后順序，所在樓層數混合編號。具體測點編號分布如圖2所示。

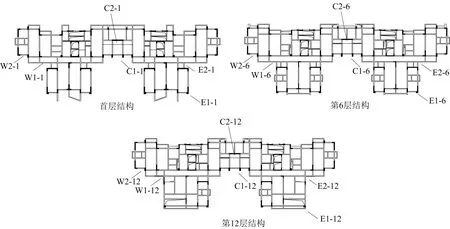
注：E1-1-柱子；E2-1-工具間；W1-1-窗臺；W2-1-窗臺；C1-1-窗臺；C2-1-樓板；E1-6-陽臺；E2-6-陽臺；W1-6-陽臺；W2-6-柱子；C1-6-窗臺；C2-6-樓板；E1-12-陽臺；E2-12-衛生間；W1-12-窗臺；W2-12-柱子；C1-12-窗臺；C2-12-樓板。

2 爆破振動監測結果與分析

2.1 振速隨爆心距變化規律分析

地表測點測得的x、y、z方向峰值振動速度如表1所示。

表1 地表測點振動數據

根據表1得到地表測點爆破振動速度隨距爆破點水平距離的變化趨勢如圖3所示。

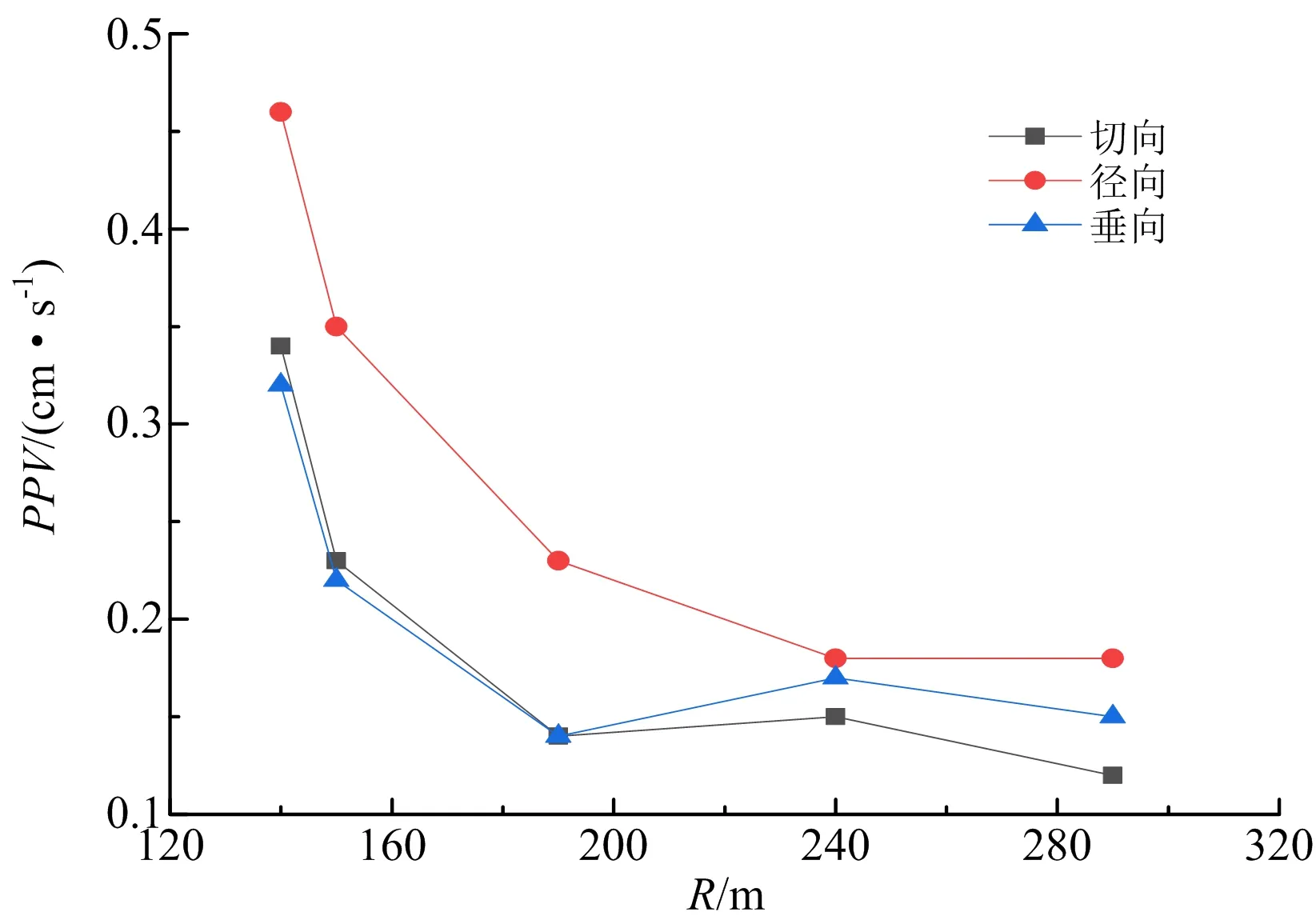
圖3 地表測點振速隨爆心距變化Fig.3 Change of vibration velocity of ground measuring points with the distance between blasting centers

由圖3可知，隨著距爆破點水平距離的增加，切向、徑向和垂向振速逐漸減小且衰減趨勢相同：距爆破點距離近時，振速衰減較快；距爆破點距離遠時，振速基本無衰減。同時，地表測點徑向振速大于切向和垂向速度。

為判斷地表測點振速是否合理以及分析爆破地震波傳播規律，對爆破振動質點速度采用薩道夫斯基公式進行回歸分析。由于監測測點位于地表平面與爆破作業爆源點的高程差相對較小，所以不考慮高程差的影響。本文參考文獻[6]所采用的薩道夫斯基模對振速進行擬合，其表達式如下：

(1)

式中：v為測點x、y、z方向最大振動速度，cm/s；Q為最大段藥量，kg；R為爆源至測點的水平距離，m；K、α為與地質特征相關的系數。

按照最小二乘法原理，對振動數據進行回歸分析，得擬合結果如圖4所示。其線性回歸系數r2為0.879，大于0.85，表明本文擬合結果較好，能真實反映測點振動速度數據。通過擬合公式計算得K=26.05,α=1.28，由此可得該區域爆破地震波峰值振速衰減公式，如式(2)所示。

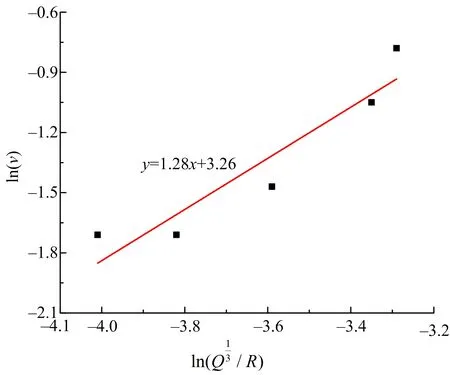
圖4 地表測點振速回歸分析Fig.4 Regression analysis of vibration velocity of ground measuring points

(2)

2.2 結構振動速度規律分析

地表測點峰值速度對應主振頻率如表2所示。

表2 地表測點主振頻率

為了研究結構構件振速與地基頻率的關系，參考文獻[16]可得爆破振動主頻預測公式為

(3)

式中：f為爆破振動主頻預測值，Hz；Kf、γ為與地質特征相關的系數。

按照最小二乘法原理，對振動數據進行回歸分析。線性回歸系數r2為0.954，表明爆破振動主頻預測公式擬合較好，測點主頻數據較為可靠，Kf=18.65,r=—1.697 1，由此可得該區域爆破地震波主頻預測公式：

(4)

由式4可得，當監測點布置在C棟內部時，C棟地基頻率為f=8.6 Hz。建筑內部測點振動峰值速度及主振頻率如表3所示。

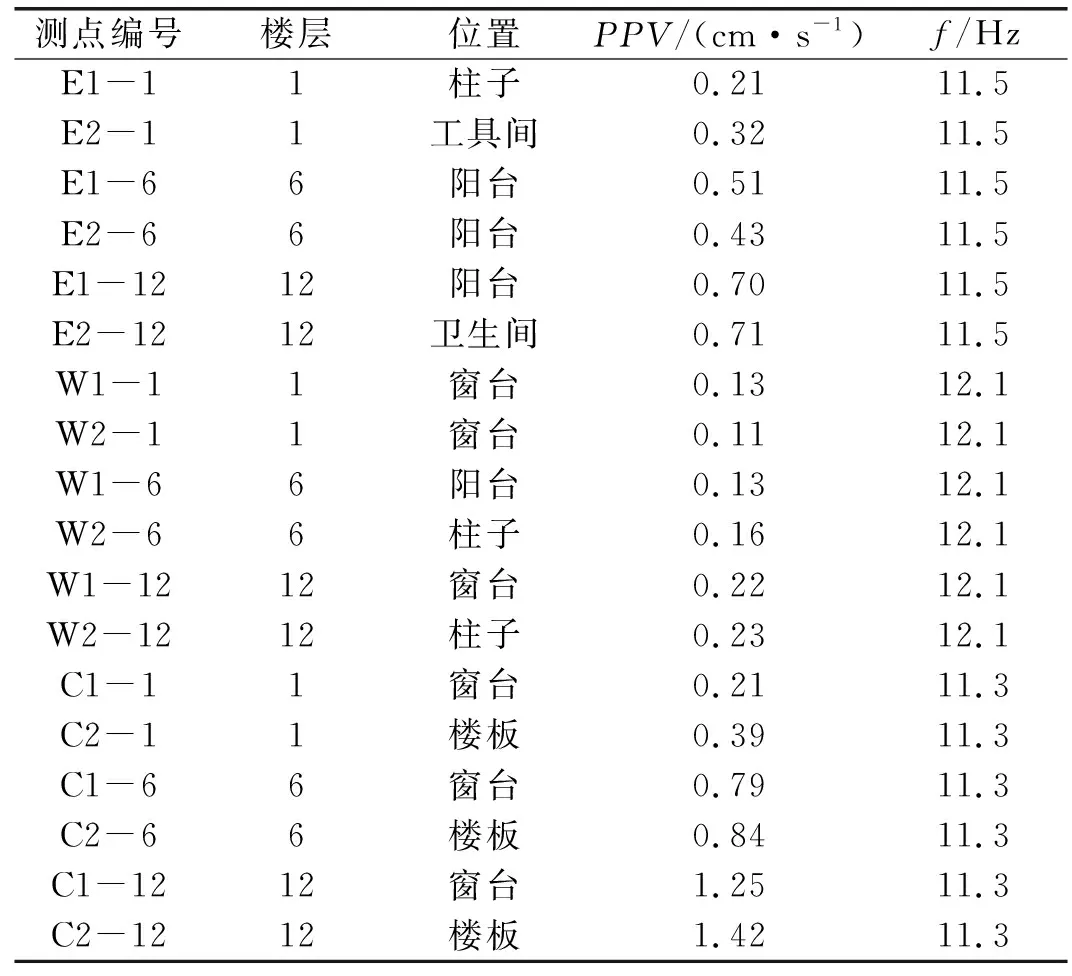
表3 結構內部測點峰值振速及頻率

由于爆破荷載為非周期荷載，可采用主振頻率表示為結構構件自振頻率，其僅與自身的質量和剛度有關。故在實際監測中，C棟建筑的東側、西側和中間結構質量和剛度的差異使得結構自振頻率不同，在監測的建筑主體和各局部構件引發的振動各不相同。為探究結構自身振動響應與頻率的關系。定義λ為頻比系數，即局部結構監測的主振頻率和地基主振頻率的比值：

(5)

式中：fw為地基礎主頻，Hz；fc為局部結構振動主頻，Hz。

對同一樓層、相同頻率結構局部振速取合速度，得到結構局部振速相比于地基速度的放大倍數和不同高程、頻比系數的關系如表4所示。振速放大倍數隨距地高程變化如圖5所示。

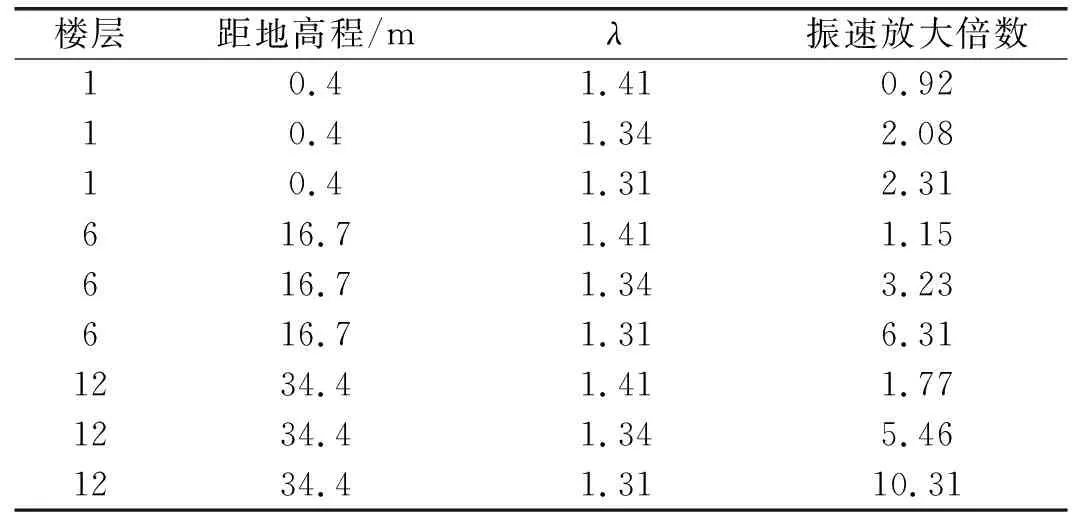
表4 結構局部峰值振速與高程、頻比系數的關系

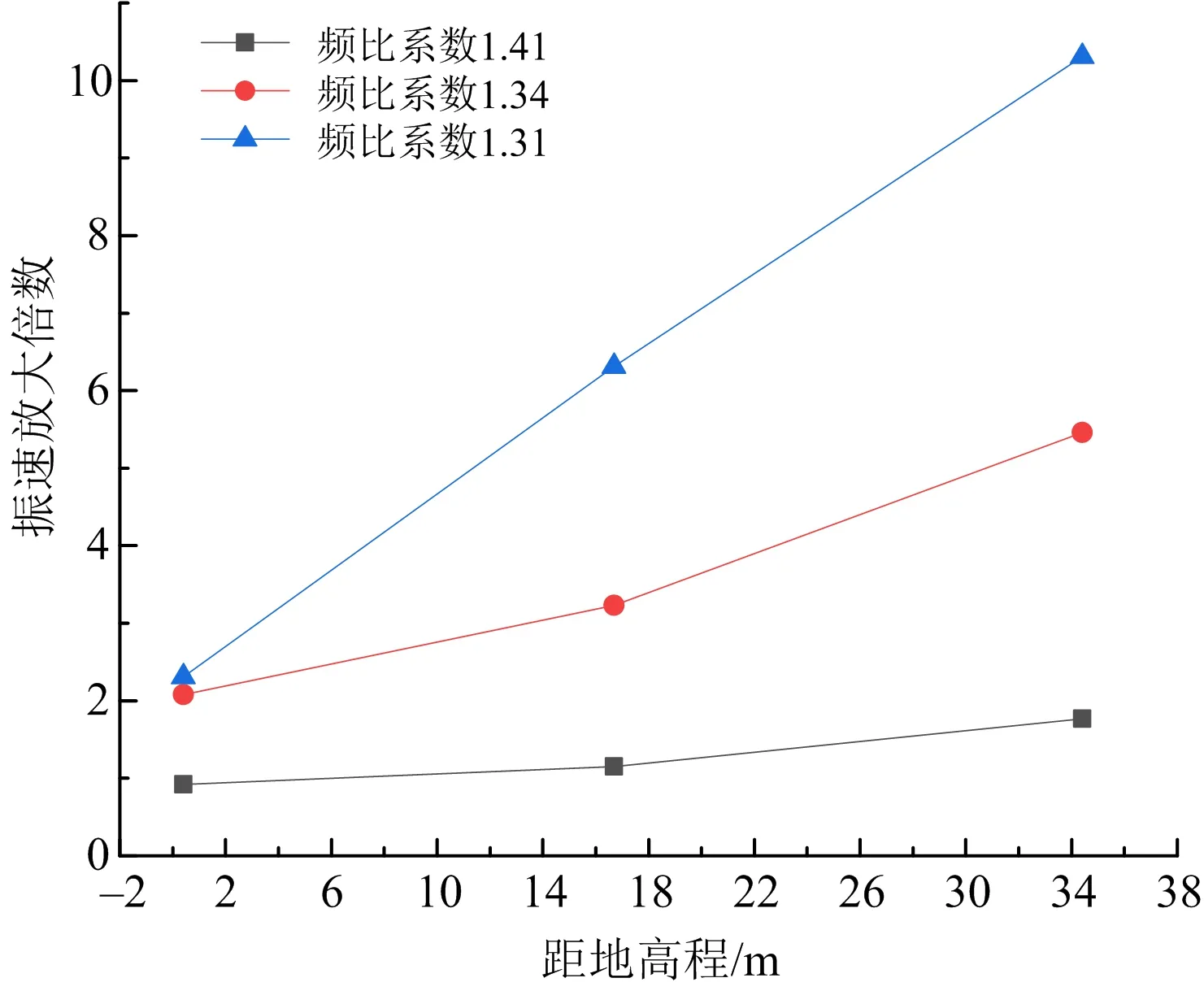
圖5 振速放大倍數隨距地高程變化Fig.5 Magnification of vibration velocity varies with the elevation above ground

由圖5可知，在頻比系數相同的情況下，隨著距地高程的增加，振速放大倍數逐漸增大；在距地高程相同的情況下，隨著頻比系數的減小，振速放大倍數明顯增大。在本次框架-剪力墻結構監測結果表明：在同一頻比系數下，框架-剪力墻結構隨著距地高差的增加，振速放大倍數呈線性增長。而隨著頻比系數的減小，線性系數值也增大，在頻比系數為1.41時，建筑高度增加16 m，振速放大倍數平均增大35%；在頻比系數為1.34時，建筑高度增加16 m，振速放大倍數平均增大150%；在頻比系數為1.31時，建筑高度增加16 m，振速放大倍數平均增大400%。在頻比系數增加量相同的情況下，隨距地高程的增加，振速放大倍數增加量逐漸增大。頻比系數增大0.01，在距地高程0.4、16.4、34.4 m時，振速放大倍數增大0.1、1.0、1.8倍。

3 結論

1)爆破振動作用下地表質點各向峰值振速隨爆心距的增大而減小，各點徑向振動速度大于垂向和切向速度。

2)隨著距爆破點水平距離的增加，地表質點x、y、z方向的振速逐漸減小，其速度衰減趨勢相同：距離爆源較近的區域，地表質點振速衰減較快，距離爆源較遠的區域，地表質點振速衰減較慢。

3)結構內部振速存在局部放大效應。在同一頻比系數下，隨著距地高程的增加，振速放大倍數呈線性增長，隨著頻比系數的減小，線性增長系數值也增大，建筑高度增加16 m，在頻比系數為1.41、1.34、1.31時，振速放大倍數平均增大0.35、1.5、4倍。

4) 多層框架-剪力墻結構在爆破地震波作用下，在頻比系數增加量相同的情況下，隨距地高程的增加，振速放大倍數增加量逐漸增大。頻比系數每增大0.01，在距地高程0.4、16.4、34.4 m時，其振速放大倍速增大0.1、1.0、1.8倍。中部頂層樓板結構在距地34.4 m、頻比系數為1.31時，振速放大倍數約為10倍，應對此處進行重點監測，必要時可采取減少爆破炸藥量、建筑物周圍開挖減振溝等方式實現減振效果。