基于核密度估計和Copula函數的風、光出力場景生成

宋 宇 李 涵

基于核密度估計和Copula函數的風、光出力場景生成

宋 宇 李 涵

（國網江蘇省電力有限公司檢修分公司，南京 211102）

新能源的隨機性、波動性及間歇性為電力系統規劃帶來困擾，對風、光出力的變化規律進行合理刻畫，生成典型出力場景是新能源規劃的常用方法。針對具有相關性的風、光出力典型場景難以生成的問題，本文首先應用非參數核密度估計法對大量樣本數據進行擬合，并進行擬合優度及精度檢驗，得到風、光的核密度估計表達式，然后建立多種基于Copula函數的風、光電場出力聯合分布模型，判斷各個模型的擬合優度，結合各個模型的Kendall與Spearman相關系數，選取最優Copula函數作為風電、光伏聯合概率分布，最后采用最優Copula聯合概率分布生成風、光年出力場景。算例分析表明，所得的風、光年出力場景符合其相關性，在反映某地區風光實際出力時有更高的準確性，可為電力系統可靠性分析和電網規劃提供參考。

核密度估計；Copula函數；場景生成；互補特性；差異系數

0 引言

以風電、光伏為代表的新能源發電存在顯著差異性，如果不采取措施就直接接入電網，會對電網的可靠性和穩定運行造成很大影響。風電、光伏等間歇性能源的建模成為新能源消納問題的基礎研究課題。同一地區的風電場和光伏電站具有較強的統計學規律及相關性，而電力系統的中、長期規劃均需基于風、光自身的出力特性，以大量場景基礎進行分析計算，來評估規劃方案的可行性和合理性。因此，考慮其相關特性，建立合適的風、光聯合出力模型，生成典型場景，對電力系統規劃有重要 意義。

當下很多研究人員嘗試使用Copula理論研究風、光出力相關性的問題[1-3]。文獻[4]首先提出一種基于Copula的計算風光出力聯合概率分布的方法，然后利用聚類算法進行模型誤差分析，該模型考慮了不同環境下二者的影響與變化關系，使風、光出力的預測準確性大大提高。文獻[5]分析了傳統Copula方法的不足之處，提出一種新的動態式的Copula函數模型，該模型計算了8組不同實例的動態相關性，驗證了所提模型的準確性與合理性。文獻[6]用阿基米德族Copula函數對多風電場聯合出力進行建模，并用正態Copula函數進行比較，證明了阿基米德族Copula函數解決此類問題的優越性。

然而，現有僅建立單個Copula模型的方法無法可靠地驗證所選取的Copula函數是否為模型中的最優函數，造成生成的典型出力場景與實際情況出入較大。因此，仍需對Copula函數進行研究與改進，選取最優Copula函數。

本文采用非參數核密度估計法對實際數據進行擬合，經擬合優度及精度檢驗后，得到風、光出力的核密度表達式。然后建立多種基于Copula函數的風、光電場出力聯合分布模型，結合各模型的Kendall與Spearman相關系數，將各Copula分布函數與經驗Copula函數比較，并判斷與經驗Copula函數的歐氏距離，選取最優Copula函數作為風電、光伏聯合概率分布，從而生成風、光出力典型場景。算例分析表明，本文所提方法生成的風、光年出力場景符合其相關性，在反映地區風光實際出力時有較高的準確性。

1 核密度估計及模型檢驗方法

研究風速大小與光照強度概率分布模型時，通常采用兩種方法，即理論分布模型與核密度估計法，前者基于參數，而后者基于非參數。基于參數估計的方法需要事先規定其符合的特定分布，一定程度上忽略了風速曲線與光照強度曲線本身具有的特征，導致參數分布模型擬合得到的結果很大程度地偏離數據實際分布[7]。非參數方法不需要提前知曉樣本的模型，以已有樣本為基礎即可挖掘出數據的分布特征[8]。

1.1 核密度估計法

式中：為樣本數量；為窗寬；(·)為核函數。

核密度估計法不需要事先假設樣本數據所符合的分布，可以直接對風電功率與光伏功率的數據進行非參數估計，從而得到各自的概率密度函數。

除了核函數會影響核密度估計的結果，窗寬也是一個需要優化的參數。其估計值與實際值的積分方均誤差為

式中，為權值矩陣。將式（2）最小化得出的o代入式（1）取出可得到總體的核估計值。

1.2 模型檢驗方法

1）擬合優度檢驗

在完成概率密度的擬合之后，需要對擬合的效果進行檢驗。通過對擬合效果的檢驗，可以衡量出各個擬合方法對原始數據的擬合優劣程度，從而選取出最佳擬合函數。常用的檢驗方法有兩種[9]，分別為Pearson2與K-S（Kolmogorov-Smirnov）。

（1）Pearson2

式中：v為第個區間內的樣本數量；p為其落在第個區間內的理論值。

式中，(·)表示事件發生的概率。

（2）Kolmogorov-Smirnov

Pearson2需要將樣本空間劃分成個子空間，導致檢驗結果隨區間選取的變化而變化，而Kolmogorov-Smirnov檢驗具有良好的適用性。

基于原始樣本，求得經驗累積分布函數F()為

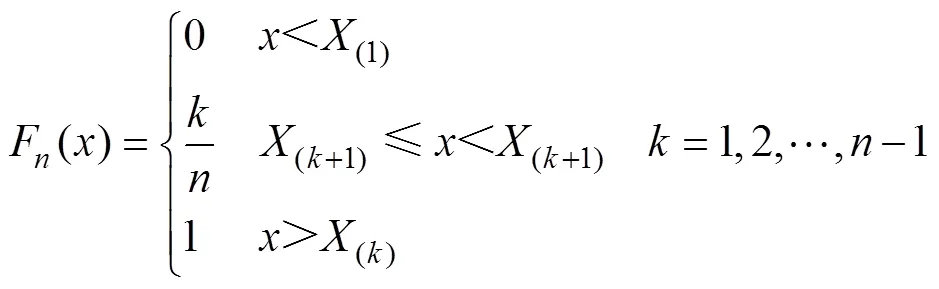
基于理論累積分布0()和經驗累積分布F()之間的最大垂直差距定義為檢驗統計量D，有

式中，為第個抽樣區間。

理論分布模型的參數可由實際歷史數據得到，在此情況下，當一個理論分布在檢驗中被拒絕時，則K-S檢驗產生的誤差相對較小。

2）擬合精度檢驗

擬合精度檢驗是從定量的角度去衡量風光出力概率模型與實際出力的頻度分布曲線之間的不同。采用平均百分比誤差（mean absolute percentage error, MAPE）與方均根誤差（root mean square error, RMSE）兩個指標衡量模型的擬合精度。

式中：為區間個數；oi、gi分別為風電和光伏標準化輸出功率正交級數密度分布和直方圖在第個區間的概率。

2 基于Copula理論的風光出力相關性建模及出力場景生成

2.1 Copula相關理論

1）Copula函數與相關系數

Copula的表達式為

常見的Copula有兩個族，分別為阿基米德Copula與橢圓Copula。阿基米德Copula函數最常見的三種為Gumbel Copula、Clayton Copula和Frank Copula，橢圓Copula函數主要包括正態Copula和t-Copula兩種。

相關系數用以反映變量之間的線性相關程度。常用的相關系數包括Kendall與Spearman秩相關系數[9]。

2）Copula函數的最優選擇

由于Copula函數的類型眾多，無法直接選取最優Copula，因此需對其進行擬合優度判別，從而選取最優函數。常用的方法包括函數圖像判別法、相關系數判別法及歐氏距離判別法。

（1）函數圖像判別法是將各Copula函數概率密度函數圖像與樣本數據的概率密度函數進行比較，圖像最為接近的即為最優Copula函數。

（2）相關系數判別法是通過Kendall秩相關系數、Spearman秩相關系數判別其擬合優度。將各類Copula函數的秩相關系數與樣本數據的秩相關系數相比較，數據越接近，其擬合優度越好，相應的Copula函數即為最優。

設具有相關性的風電場和光伏電站的出力分別為和。（1,1）和（2,2）是其出力（,）的任意兩個出力樣本觀測值，兩個值相互獨立。如果(1,1)·(2,2)＞0，則稱（1,1）和（2,2）具有一致性；如果(1,1)·(2,2)＜0，則稱（1,1）和（2,2）具有不一致性。

（3）歐式距離判別法是用各Copula函數與樣本數據的經驗Copula函數的歐式距離比較，歐式距離越小，則Copula函數的擬合優度越好。

利用平方歐式距離選取最優Copula函數。平方歐式距離的定義為

2.2 風光場景生成與互補特性

1）基于蒙特卡洛的風光出力靜態場景生成

選取了最佳Copula函數之后，應對Copula函數進行采樣，從而生成大量樣本，其主要步驟如 下[11-14]：

（1）在[0, 1]區間內隨機產生數字1,2,…,a。

（2）令第一個隨機變量邊緣分布函數值1=1，根據2.1節中選定好的Copula函數來求得第二個隨機變量邊緣分布函數值2，即求式（14）的解。

（3）對于第個隨機變量的邊緣分布函數值u，即求式（15）的解。

（4）重復上述步驟（1）、（2）、（3）次，則可以得到組個隨機變量的邊緣分布函數值。

在對風電與光伏出力進行分析計算時，在步驟（5）的反函數運算中，首先基于Copula聯合概率密度分別求出二者的邊緣分布函數，然后再分別進行反函數的運算。通過這種計算方式，使所生成的場景充分考慮了風光出力的相關性。場景生成步驟如圖1所示。

圖1 風電出力與光伏出力的場景生成步驟

利用場景生成得到的數據量龐大，且各個場景之間相似度高。為實現相近場景的有效合并，采用后向縮減法[15]（backward reduction, BR）進行場景縮減。基于后向縮減法的場景縮減流程如圖2所示。

圖2 基于后向縮減法的場景縮減流程

2）風光互補特性指標

采用差異系數（coefficient of variation, CV）來表征風光出力的互補特性，CV的定義為[16]

從式（16）可以看出，CV越小，風電與光伏所共同輸出的功率越平穩，風光互補特性就越好。

3 算例分析

以某地區2020年全年的風速、光強為例，風速與光強的數據采樣間隔為1h。采用正態分布、威布爾分布及核密度估計分別對風速數據進行擬合，正態分布、威布爾分布的參數采用極大似然估計來確定，風速參數擬合結果見表1，擬合效果如圖3所示。

表1 風速參數擬合結果

這三種方法的擬合優度及擬合精度的檢驗結果見表2。

表2 不同擬合方法的擬合優度與擬合精度檢驗結果

其中，Pearson2的臨界值為21.598，K-S的臨界值為0.006 5。

威布爾分布與正態分布擬合相當，MAPE與RMSE的值接近，且均能通過Pearson2的檢驗，相對來說，正態分布的效果更優一些，但均未能通過K-S檢驗。而非參數核密度估計各項檢驗標準的值均遠遠小于參數估計的值，其擬合的效果更優。

對光照數據采用同樣的方法進行處理，對比Beta分布與非參數核密度分布的擬合情況，參數擬合結果見表3，擬合效果如圖4所示。由于Beta分布是定義在[0, 1]區間內的連續概率分布，因此此處將光照強度進行歸一化處理。

表3 光照強度參數擬合結果

從圖4中可以看出，核密度估計的擬合效果要遠遠優于Beta分布的擬合效果。

綜上所述，核密度估計在擬合風光數據方面具有較好的適用性，對該地風電出力、光伏出力直接進行擬合，可避免擬合后數據轉換造成的誤差。該地光伏電站的額定功率為100MW，風電機組的額定功率為80MW。計算窗寬：風電數據總數1=8 760，標準差1=0.176，窗寬1=0.030 3；光伏數據總數2= 8 760，標準差2=0.291，窗寬2=0.050 2。

然后進行非參數核密度估計，并對擬合結果進行擬合優度與精度檢驗，結果見表4。其中，Pearson2的臨界值為18.694，K-S的臨界值為0.036 5。從表4可以看出，在對風電出力與光伏出力的數據進行擬合時，利用核密度估計法進行概率密度擬合，可滿足擬合優度檢驗及擬合精度檢驗，風光的核密度估計具體表達式為

表4 基于核密度估計的風光出力擬合檢驗結果

式中，X為風光實際樣本值。

基于五種Copula函數，分別建立風電場與光伏電站有功功率出力的預測誤差聯合分布函數，如圖5、圖6所示。

圖5 橢圓族Copula的密度函數與分布函數

計算經驗Copula累積分布函數，如圖7所示。

圖7 經驗Copula分布函數

從圖5～圖7可以看出，Frank-Copula的分布函數與經驗Copula的分布函數最為接近。

然后，依次計算各個Copula函數的Kendall秩相關系數、Spearman秩相關系數及每一種Copula與經驗Copula函數的平方歐式距離，結果見表5。

表5 各Copula函數的相關系數與平方歐氏距離

從表5可以看出，使用Frank-Copula法計算得到的各相關系數與樣本數據的相關系數較為接近，而且Frank-Copula與經驗Copula的歐式距離在所有結果中是最小的。除此以外，Frank-Copula函數可以同時考慮變量的非負與負相關的關系，恰好風電出力與光伏出力互補、具有負相關的關系。雖然表5中t-Copula的相關系數也比較良好，但由于其與經驗Copula的歐式距離過大，說明該類型Copula函數擬合效果不佳，因此不太適合將t-Copula作為最優擬合函數。綜上所述，本文選取Frank- Copula進行數據擬合，從而保證了擬合的精度。

采用Frank-Copula函數進行擬合，利用極大似然估計法進行參數的估計，得=0.285。聯合分布函數的表達式為

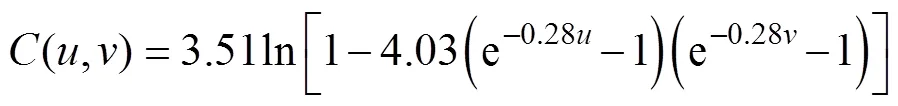
對24個時段風電出力數據與光伏出力數據分別進行Frank-Copula函數擬合，然后利用蒙特卡洛采樣生成場景。

基于2.2節的場景生成方法，生成500個風光互補場景，然后利用后向縮減法分別對生成的大量風電與光伏場景進行縮減，并求出每個場景的概率，如圖8、圖9所示，圖中的出力均為標幺值。縮減后各個場景的概率見表6。

圖8 風電出力縮減場景

圖9 光伏出力縮減場景

采用差異系數CV衡量所生成風電出力與光伏出力的互補特性，按照上述計算過程進行年度場景生成5次，得到5組年度數據，差異系數比較見表7。

表6 縮減后各場景的概率

表7 差異系數比較

4 結論

本文基于非參數核密度估計法，利用多種Copula函數建立風光聯合時序出力模型，通過比較各秩相關系數與平方歐氏距離，選取最優Copula函數對各個時刻的風電出力數據與光伏出力數據進行擬合，得到每個時刻的考慮風光出力相關性的概率密度函數，利用Copula函數的蒙特卡洛采樣方法生成年度場景。以江蘇某地區年度風光實際出力數據為例，驗證所提方法及模型，分析結果表明：

1）非參數核密度估計法較參數估計法能更好地擬合樣本數據，所得模型更接近真實值。

2）所提基于最優Copula函數的蒙特卡洛采樣方法能夠生成具備互補特性的風、光年出力場景，可應用在電力系統規劃模型中，能夠為電力系統可靠性分析提供數據基礎。

[1] HOICKA C E, ROWLANDS I H. Solar and wind resource complementarity: advancing options for renewable electricity integration in Ontario, Canada[J]. Renewable Energy, 2011, 36(1): 97-107.

[2] 喬延輝, 韓爽, 許彥平, 等. 基于天氣分型的風光出力互補性分析方法[J]. 電力系統自動化, 2021, 45(2): 82-88.

[3] 白樺, 王正用, 李晨, 等. 面向電網側、新能源側及用戶側的儲能容量配置方法研究[J]. 電氣技術, 2021, 22(1): 8-13.

[4] 鐘嘉慶, 李茂林, 江靜, 等. 基于Copula理論的風/光出力預測誤差分析方法的研究[J]. 電工電能新技術, 2017, 36(6): 39-46.

[5] 偲默, 苗世洪, 霍雪松, 等. 基于動態Copula的風光聯合出力建模及動態相關性分析[J]. 電力系統保護與控制, 2019, 47(5): 35-42.

[6] HAGHI H V, BINA M T, GOLKAR M A, et al. Using copulas for analysis of large datasets in renewable distributed generation: PV and wind power integration in Iran[J]. Renewable Energy, 2010, 35(9): 1991-2000.

[7] 周澤人, 舒印彪, 董存, 等. 基于混合威布爾分布的風能資源分布統計分析研究[J]. 數理統計與管理, 2020, 39(4): 584-594.

[8] 賴昌偉, 黎靜華, 陳博, 等. 光伏發電出力預測技術研究綜述[J]. 電工技術學報, 2019, 34(6): 1201-1217.

[9] 李鵬. 電力需求響應機制下含電池儲能系統的風光互補發電系統經濟調度研究[J]. 電氣技術, 2015, 16(3): 57-60.

[10] 白順明, 陳磊, 姜飛, 等. 考慮風電最大化消納的電力系統多目標優化[J]. 電氣技術, 2020, 21(1): 7-11.

[11] 吳治均, 李明昆. 基于饋線路徑集合法的并網型微電網可靠性評估[J]. 電氣技術, 2016, 17(10): 17-22.

[12] 黎靜華, 文勁宇, 程時杰, 等. 考慮多風電場出力Copula相關關系的場景生成方法[J]. 中國電機工程學報, 2013, 33(16): 30-36, 21.

[13] 楊楠, 黃禹, 葉迪, 等. 基于自適應多變量非參數核密度估計的多風電場出力相關性建模[J]. 中國電機工程學報, 2018, 38(13): 3805-3812.

[14] ARIK I, KANTAR Y M, USTA I. The new odd-Burr Rayleigh distribution for wind speed characterization[J]. Wind & Structures, 2019, 28(6): 369-380.

[15] 車兵, 李軒, 鄭建勇, 等. 基于LHS與BR的風電出力場景分析研究[J]. 電力工程技術, 2020, 39(6): 213-219.

[16] 周博, 艾小猛, 方家琨, 等. 計及超分辨率風電出力不確定性的連續時間魯棒機組組合[J]. 電工技術學報, 2021, 36(7): 1456-1467.

Typical scene generation of wind and photovoltaic power output based on kernel density estimation and Copula function

SONG Yu LI Han

(State Grid Jiangsu Electric Power Co., Ltd Maintenance Branch Company, Nanjing 211102)

The randomness, volatility and intermittent nature of new energy resources bring troubles to power system planning. A reasonable description of how wind power and photovoltaic output behave and generating typical output scene is a common method for new energy planning. A method for generating typical scene of relevant wind power and photovoltaic output is proposed. This paper firstly fits a large number of sample data based on kernel density estimation, and performs fitting and pre-test to obtain a kernel density estimation expression of wind and photovoltaic power output. This paper builds a variety of combined distribution models of wind and photovoltaic power based on Copula functions, and then judges the fitness of each model. The Kendall and Spearman correlation coefficients of each model are considered to select the optimal Copula function as wind power, photovoltaic joint probability distribution. Finally, the annual power output of wind and photovoltaic power is generated based on the optimal Copula joint probability distribution. Case analysis shows that the simulation results of annual output of wind and photovoltaic power meets their relevance, and has higher accuracy in wind and photovoltaic power output in the reaction. There must be a certain reference value for the reliability analysis of power system and grid planning.

kernel density estimation; Copula function; scene generation; complementary characteri- stics; difference coefficient

2021-08-30

2021-10-08

宋 宇（1989—），男，江蘇省南通市人，碩士，工程師，主要從事繼電保護及自動化相關工作。