基于深度學習的軟鋼力學特性

王正桓，張超鋒，陸菁，李偉力

基于深度學習的軟鋼力學特性

王正桓1a，張超鋒1b，陸菁1c，李偉力2

（1.江南大學 a.信息化建設與管理中心 b.機械工程學院 c.設計學院，江蘇 無錫 214122； 2.無錫開放大學，江蘇 無錫 214011）

針對機械工程中軟鋼材料在大塑性拉伸載荷下力學特性分析的問題，提出一種基于深度學習的分析方法來預測其力學特性。首先對軟鋼材料不同臺階角度展開拉伸實驗，并將采集到的實驗數據利用智能技術進行預測分析。實驗模型設計為雙層結構，第1層結構采用共享全連接層特征輸入，第2層使用極端隨機樹和長短時記憶網絡做聯合深度訓練，并對訓練結果經過激活函數計算后統一輸出。采用聯合訓練模型在實驗測試集上能較好地反映出應變與應力的變化趨勢、速度和數值關系。實驗結果顯示，利用聯合訓練模型比單一ET和LSTM預測技術在擬合效果上分別提高了28.3%和63.5%。利用新模型取得較好的預測效果，這為分析金屬阻尼器大塑性拉伸載荷下軟鋼材料力學特性的分析提供了重要的參考。

機械設計；力學特性；機器學習；極端隨機樹；長短時記憶網絡

金屬阻尼器是以提供運動阻力，耗減運動能量的裝置，作為一種十分重要的耗能構件，在機械工程應用和設計，以及抗震工程中應用十分廣泛[1]。機械工程中的耗能結構在設計中充分利用金屬材料的塑性變形能力，從而優化提高金屬阻尼器的耗能。在實際使用中有剪切[2]、張力[3]、彎曲和組合[4]等多種類型的阻尼器，采用不同的金屬耗能機制，在不同工況下采用不同的變形方式耗散能量。

機械工程中軟鋼材料在張力[5—6]、彎曲[7]、剪 切[8—9]等不同載荷下表現出不同的特性。同時，軟鋼材料在不同的圓角高度[10]、圓角長度[11]和肩部圓角等形狀系數也會表現出不同的性能[12]。目前，關于塑性形變下軟鋼材料應力集中及其對阻尼器變形性能影響的研究還較少。通過人工智能方法進行科學預測與分析，可以提高系統評估的科學性和可靠性，對實際應用有著積極的指導意義。

金屬材料的力學性能研究是機械設計中研究的熱點問題之一。可以采用多種技術來分析金屬材料力學性能，如有限元模型[13]、模態結構[14]等。隨著人工智能技術的廣泛應用，將人工智能技術方法用于金屬材料力學性能研究已成為一種重要的技術手段。如將神經網絡[15]、支持向量機[16]等技術應用于該領域，以及在包裝機械設備的故障識別[17]、包裝缺陷檢測[18]中都有著重要的應用。

在人工智能技術中，時間序列預測作為一種重要的預測手段，在各個領域都有重要應用。在機械工程阻尼器的形變中，隨著拉伸載荷的應變變化應力發生相應變化，每一時刻的不同形變和上一時刻有關聯，因此可以利用長短期記憶網絡（Long Short-Term Memory，LSTM）[19]分析不同時刻的應變與應力的連貫變化，以對金屬阻尼器的材料力學特性進行分析預測。LSTM是一種時間循環神經網絡，是為了解決一般循環神經網絡存在的長期依賴問題而設計，在時序和類時序問題中有良好的表現。

極端隨機樹[20]（Extremely randomized trees，ET）在使用中表現非常穩定，即使數據集中出現了一個新的數據點，整個算法也不會受到過多影響，只會影響一棵決策樹，很難對所有決策樹產生影響。同時，極端隨機樹不采用隨機采樣，即每個決策樹采用原始訓練集。通過該方法可較好提高分析軟鋼材料性能的可靠性。

文中采用深度學習中的LSTM方法，同時利用共享嵌入層結合極端隨機樹技術進行聯合訓練。首先對帶有臺階的軟鋼性能展開研究，然后采用LSTM和ET進行聯合訓練的方法，同時提高預測的擬合度，從而合理地評估和預測軟鋼材料的力學性能，為機械工程中阻尼器的設計提供依據。

1 研究計劃

為研究分析金屬阻尼器軟鋼結構材料在不同塑性變形下的應力應變情況，設置了3種不同截面高度的突變處（稱為“臺階”）角度來展開研究，具體研究計劃見表1。

為了能更準確反映該種鋼材料應變應力的變化狀態情況，采用聯合訓練的方法來提高學習分析的效果，進一步減少偏差。總體思路流程見圖1。

首先采用2種基礎算法對軟鋼T30的實驗結果進行分析。然后建立共享嵌入層將輸入特征作為ET和LSTM等2種算法的共同輸入。利用共享層對輸入特征同時進行ET算法學習和LSTM算法學習，利用ET模型學習特征的變化關系，分析其在不斷應變過程中的對應應力情況；對于LSTM模型，嵌入層將實驗數據按序列順序輸入模型，使其學習在拉伸載荷作用下的應力隨應變變化的序列特點，將LSTM的輸出和ET模型的輸出經過激活函數后再輸出。最后，利用T45和T60實驗結果，通過殘差分析來驗證該優化融合模型的合理性、準確性和可靠性。

1.1 阻尼器軟鋼試樣

軟鋼阻尼器的臺階在塑性變形下的損傷比較復雜。在往復循環載荷下，臺階的損傷特性研究仍不充分。在實際工況中，T形臺階的角度不再是一個定值，而是隨著剪切振幅的變化而變化，因此，在T形臺階中設計了3個角度（=30°，45°，60°），結合智能技術研究力學性能的變化，分析及預測其在3種不同角度下的應變應力變化情況。軟鋼試樣見圖2。

1.2 算法研究

1.2.1 LSTM算法

長短記憶神經網絡（LSTM）是一種特殊的循環神經網絡，能夠學習長期依賴關系，在各種時序問題上表現良好，現已被廣泛使用。一個典型的 LSTM 網絡由不同的單元或記憶塊組成，LSTM單元一般會輸出2種狀態到下一個單元，即單元狀態和隱藏狀態。記憶塊則負責記憶各個隱藏狀態或前面時間步的事件。典型單元結構見圖3。

圖2 軟鋼試樣

圖3 LSTM單元結構

在每個時間點n，都會有一個對應的狀態C，C記錄了之前的信息。在每個時間點，都可以通過調節權重的輸入、遺忘等方式去修正t的狀態。通過使用sigmoid門來控制每個輸入因素對于C的影響值，一般使用遺忘門、輸入門、輸出門等3個門的控制來實現對長短時記憶的分析。LSTM由3個主要組成部分構成，即遺忘門、輸入門、輸出門。通過遺忘門、輸入門、輸出門對狀態的影響，最終決定每個時間點的輸出狀態，最后把這個狀態一直傳遞下去，從而達到控制長短時記憶的目的。LSTM主要構成部件見表2。

表2 LSTM主要構成部件

LSTM在時刻輸入x，首先取上個階段的輸出h?1，通過sigmoid函數來控制時刻的狀態。然后創建1個備選的，用tanh函數控制部分，再把這2個部分相乘。同時，再加上遺忘門的輸出，構成當前時刻的C，即：

(1)

式中：f為遺忘門的輸出。

(2)

式中：W表示遺忘門輸出時在h-1和輸入下所對應的權重值。在得到C的狀態輸出后，由輸出門控制可以看到，通過sigmoid函數處理信號的輸出，輸出門控制C的哪部分被輸出，即：

(3)

式中：o表示輸出門輸出時在h-1和輸入下所對應的權重值。由輸出門的結構可以看出，C輸出經過tanh函數激活，再與O相乘，得到最后的輸 出，即：

(4)

得到時刻的最后輸出h，完成了LSTM序列處理。可以看到，LSTM通過遺忘門、輸入門、輸出門對于狀態的影響，最終決定每個時間點的狀態并傳遞下去，從而達到長短時記憶控制的作用。

1.2.2 極端隨機樹算法

極端隨機樹算法是一種多棵決策樹集成的分類器，與隨機森林類似。主要區別在于隨機森林采用的是隨機采樣bootstrap方式來選擇采樣集作為每個決策樹的訓練集，而極端隨機樹算法一般不采用隨機采樣，每個決策樹采用原始訓練集。隨機森林應用Bagging模型，極端隨機樹使用的所有樣本，只有特征是隨機選取。極端隨機樹算法見圖4。

1.2.3 聯合訓練模型

金屬阻尼器由于在拉伸載荷的不斷作用下，應力會隨著應變的增加而同時增加，但當應變到一定程度后，應力會隨著應變的增加而減小，直至為零，即此時金屬材料發生了斷裂。如果只按照序列順序進行機器學習，不能充分學習到該問題的數據特點，為充分學習數據特點，利用共享嵌入層采用ET模型和LSTM模型同時學習的方法，以達到充分學習特征變化的目的，還可以兼顧應力應變序列變化過程中的數據變化情況。聯合訓練結構見圖5。

2 結果與分析

2.1 實驗結果

經過對不同T型臺階角度的拉伸載荷，隨著不斷地施加載荷直至發生斷裂破壞，得到的實驗結果見圖6。

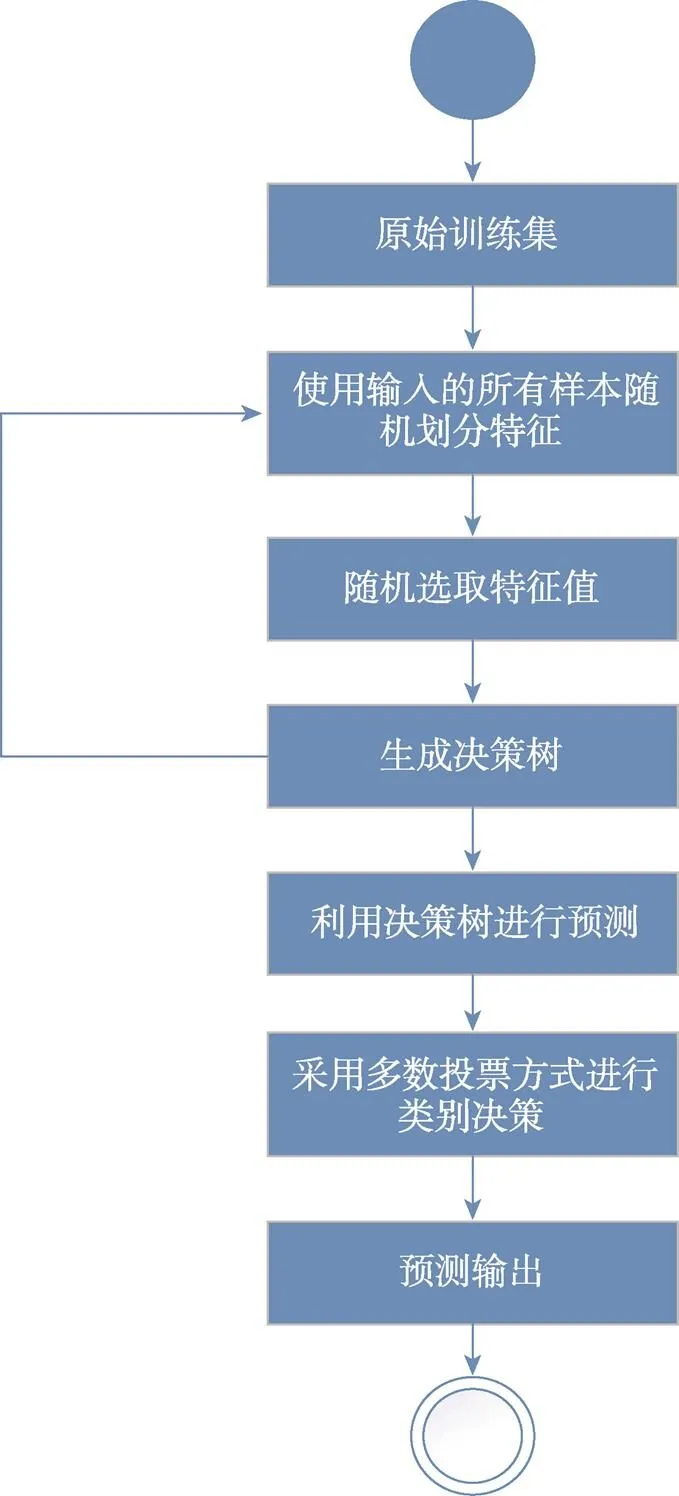
圖4 極端隨機樹算法

從實驗結果可以看出，塑性變形主要集中在中間區域。在拉伸載荷作用下，當臺階高度一定，不同臺階角度都具有較好的強化效果。

2.2 聯合訓練算法

聯合訓練算法首先對T30進行拉伸實驗，通過對T30實驗劃分不同的訓練集，及其訓練結果來確定訓練集的劃分比例。實驗按90%，80%，70%，60%來劃定拉伸載荷數據集中的訓練集比例，分別考察在不同比例情況下模型的融合預測分析效果，見表3。

表3分析了不同訓練集劃分（90%，80%，70%，60%共4種比例）下3種算法對應的預測效果，實驗采用經典的均方誤差（Mean Squared Error,MSE）指標來衡量。由表3可知，當訓練集比例為90%時，3種算法模型對應的MSE指標數值優于其他比例的對應值，ET模型MSE指標為0.2547，LSTM模型MSE指標為0.4955，融合模型效果的MSE指標為0.1833。通過縱向和橫向比較，實驗按照90%來劃定訓練集比例預測效果最好。在確定好數據比例劃分后，針對聯合訓練算法模型（圖5），采用算法實現流程（見圖7），進行基于LSTM和ET的聯合訓練。

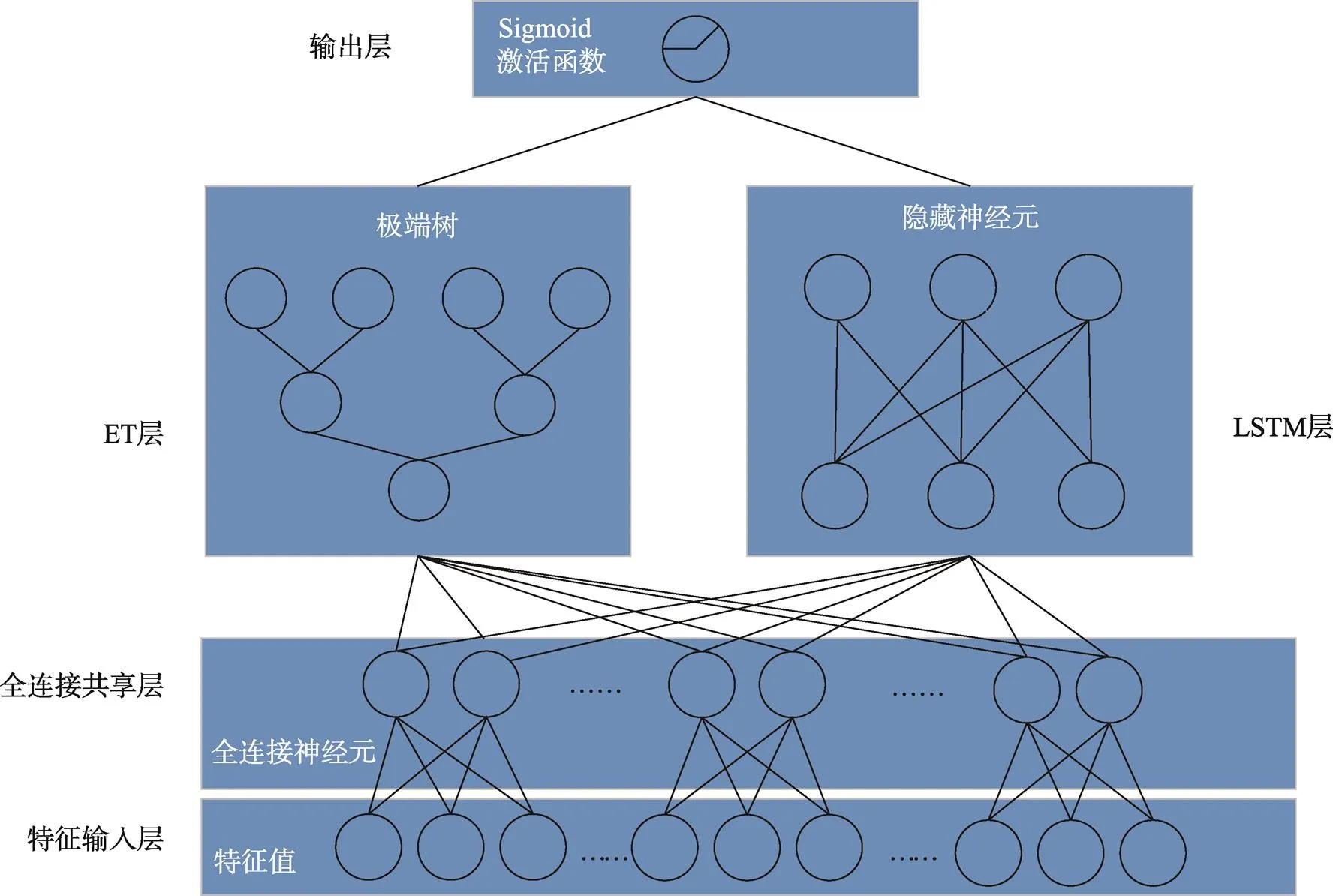
圖5 聯合訓練結構

圖6 拉伸載荷實驗結果

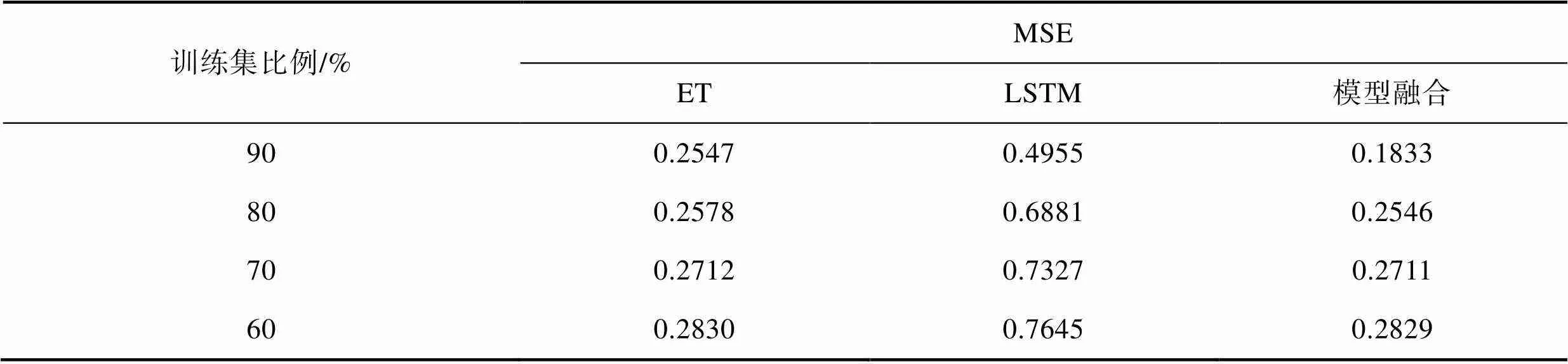
表3 不同訓練集比例劃分對比

圖7 聯合訓練算法流程

實驗對T45和T60分別進行測試，將T45和T60的應力應變測試和預測值進行分析對比，為了有效地評估應力應變變化，將整個形變過程按應力變化分為上升和下降2個過程，每個過程又分為兩端作細致考察，并對3種模型的應變應力預測進行比較分析。對ET，LSTM和聯合訓練等3種模型分別用預測1、預測2和預測3表示，預測變化曲線結果見圖8。

由圖8可知，隨著拉伸應力增長，該種阻尼器軟鋼材料的應變也呈正比例變化。在前半段應變過程中，應力預測變化隨著拉伸載荷的增加也逐步增加，變化趨于平穩，基本與實際應力值變化接近。在拉伸載荷的上升段，當應力達到峰值時開始進入下降段，預測應力變化值和真實變化值有一段變化較快。在這一段的快速變化中，預測值和真實值的變化趨勢和速度保持一致，但數值上有一定的偏差，這主要是由于此時拉伸載荷較大，形變突然加速，機器學習此時在這種情況下學習有一定的困難，使此段存在一定的差別。在實際應變過程中，此段一直處于加速狀態，應力變化激烈而快速。造成此段應力在短時間內迅速降為0，即此時該種軟鋼材料發生了斷裂。綜上所述，聯合訓練模型較好地反映了應變應力的變化情況，能較為準確地反映變化趨勢和數量。為檢驗模型的有效性與殘差，可做進一步分析。

2.3 模型檢驗分析

為了檢驗融合模型的有效性，通過殘差做進一步分析。通過方檢驗來分析，見表4。

表4中表示擬合優度，是用來衡量估計模型對觀測值的擬合程度。值接近1，說明該模型擬合性越好。由表4可知，調整后的方為0.989，擬合較好，且在3個模型中擬合效果都較好。誤差估算結果顯示，聯合模型比ET和LSTM算法分別提高了73.2%和80.9%。

為了能更好地判別模型分析的有效性，采用Anova進行分析判斷，見表5。

由表5可知，方差分析的結果是對整個回歸方程的總體檢驗。根據該分析所對應的顯著性來判斷整個回歸方程的使用價值，當顯著性小于0.05，表明該模型的分析有效。通過比較表5模型的殘差平方和大小來判斷擬合效果，殘差平方和越小，擬合效果越好。擬合結果顯示，融合模型比ET和LSTM算法分別提高了28.3%和63.5%。

通過分析殘差統計，可進一步判斷模型的預測有效性，殘差統計見表6。

圖8 拉伸載荷應力應變

表4 R方檢驗

注：a表示自由度調整

表5 Anova分析

注：b表示顯著性標識

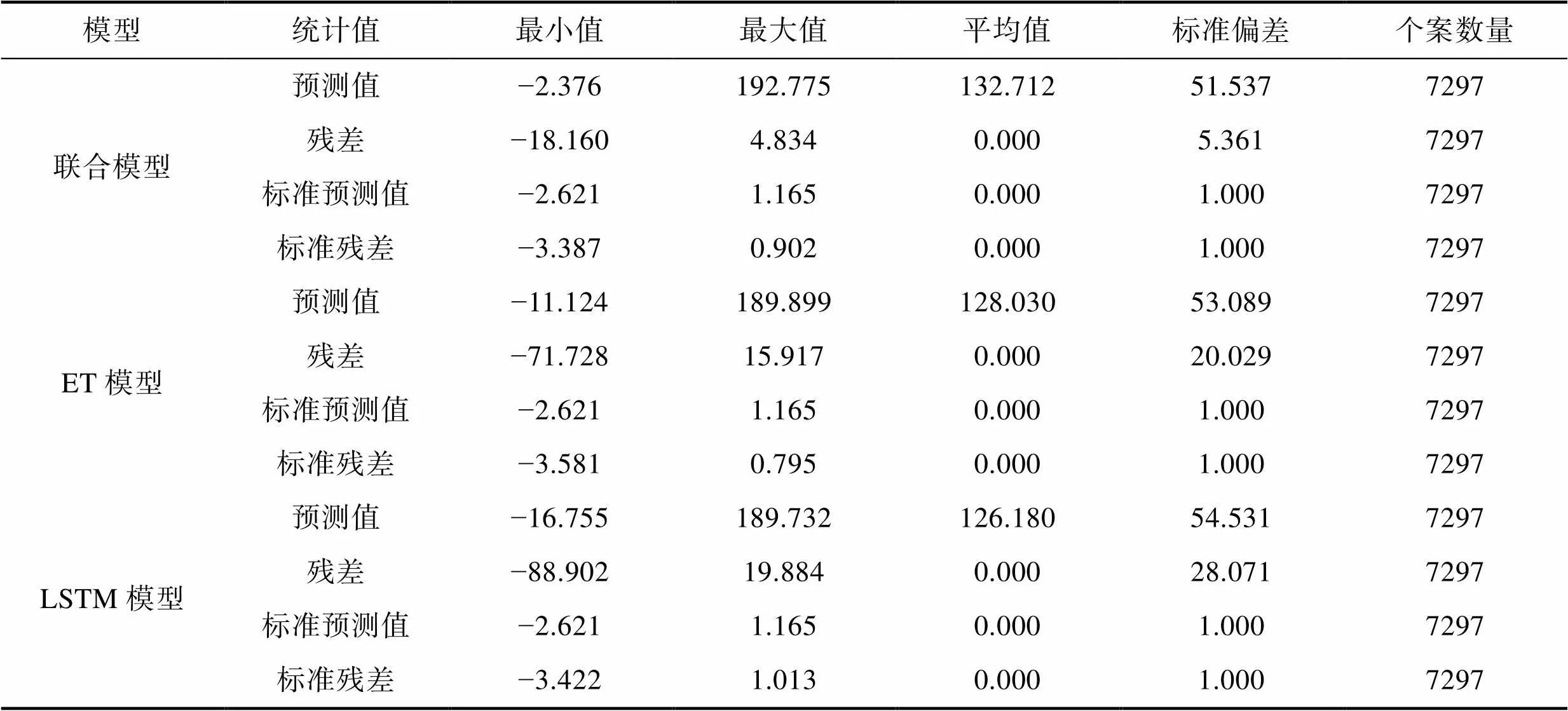
表6 殘差統計

由表6可知，3個模型的標準化殘差均值為0，偏差為1，說明該模型預測值的標準化殘差接近標準正態分布，實驗所采用的模型預測無偏估計。聯合訓練模型的標準偏差最小，聯合訓練模型預測穩定性優于ET和LSTM。

綜上所述，聯合訓練預測模型是無偏有效的預測，能較好地預測和反映軟鋼力學的特性。聯合訓練模型的預測效果優于單個模型的預測能力，并且能充分發揮各個模型的優勢，在實際應用中具有積極的參考意義。

3 結語

針對機械工程中軟鋼材料在大塑性拉伸載荷下力學特性分析的問題，采用融合模型對其進行分析和研究。該模型利用共享嵌入層的方式將ET和LSTM算法進行聯合訓練，通過不同角度的拉伸載荷，對軟鋼材料相應的應變應力情況進行了實驗分析。實驗結果顯示，模型預測值和真實值之間在變化趨勢和變化速度上都保持一致，預測數值在拉伸上升階段和下降段的后半段預測較為準確，而在形變突然加速的下降前半段的預測分析還需進一步深入研究。通過對比3種模型的擬合效果可以看出，融合模型比ET和LSTM算法分別提高了28.3%和63.5%，這表明改進后的模型對于軟鋼材料在大塑性形變下的設計和研究方面具有積極的參考意義。

[1] ZHANG Chao-feng, CHEN Shi-xi, LIN Xu-chuan, et al. Effect of T-Shape Shoulder Fillet on the Plastic Deformation Properties of SS400 and LYS160 Steel[J]. Materials (Basel, Switzerland), 2020, 13(7): 1528- 1535.

[2] YU Jin-guang, LIU Li-ming, LI Bo, et al. Comparative Study of Steel Plate Shear Walls with Different Types of Unbonded Stiffeners[J]. Journal of Constructional Steel Research, 2019(159): 384-396.

[3] RAMAZAN Ozcelik, YAGMUR Dikiciasik, ELIF FiruzeErdil. The Development of the Buckling Restrained Braces with New End Re-Strains[J]. Journalof Constructional Steel Research, 2017(138): 208-220.

[4] LI Zong-jing, SHU Gan-ping, HUANG Zhen. Development and Cyclic Testing of an Innovative Shear-Bending Combined Metallic Damper[J]. Journal of Constructional Steel Research, 2019(158): 28-40.

[5] LIU Guang-yan, ZHANG Ruo-nan, YIYa-nan, et al. Experimental and Simulation Study on Stress Concentration of Graphite Components in Tension[J]. Mechanics of Materials, 2019(130): 88-94.

[6] WALDMAN Wale, HELLER Macaulay, CHEN Gao-xin. Optimal Free-Form Shapes for Shoulder Fillets in Flat Plates Under Tension and Bending[J]. International Journal of Fatigue, 2001(23): 509-523.

[7] FRANCISCO Sanchez-marin, VICTOR Roda-casanova, ALBERTO Porras-vazquez. A New Analytical Model to Predict the Transversal Deflection Under Load of Stepped Shafts[J]. International Journal of Mechanical Sciences, 2018(147): 91-104.

[8] MEHMET Firat. A Notch Strain Calculation of a Notched Specimen Under Axial-Torsion Loadings[J]. Materials & Design 2011(32): 3876-3882.

[9] LIU Yang, MASATOSHI Shimoda. Shape Optimization of Shear Panel Damper for Improving the Deformation Ability Under Cyclic Loading[J]. Structural & Multidisciplinary Optimization, 2013(48): 427-435.

[10] HAMADA Shigeru, MORIYAMA Tsuyoshi, NOGUCHI Hiroshi. Dependence of Fatigue Limit on Step Height for Stepped 0.45% Carbon Steel with Singular Stress Field[J]. Engineering Fracture Mechanics, 2018(188): 20-35.

[11] LANSARD Rhone. Fillets without Stress Concentrations[J]. Journal of the Japan Society of Mechanical Engineers, 2015(13): 97-104.

[12] ZHANG Chao-feng, ZHU Tong-bo, WANG Long-fei, et al. Ultra-Low Cycle Fatigue Performance Evaluation of the Miniaturized Low Yield Strength Steel Shear Panel Damper[J]. Journal of Constructional Steel Research, 2017(135): 277-284.

[13] 祁荷英, 陳明明, 徐倩, 等. 基于纖維束漸進損傷性能的平紋陶瓷基復合材料拉伸力學行為預測[J]. 中國科技論文, 2018, 13(4): 444-449.

QI He-ying, CHEN Ming-ming, XU Qian, et al. Prediction of Tensile Behavior of Plain Weave Ceramic Matrix Composites From Tow Properties with Progressive Damage[J]. China Science Paper, 2018, 13(4): 444-449.

[14] 鄔開, 朱林利. 雙模態納米孿晶金屬材料的力學性能研究預測[J]. 中國科技論文, 2018, 13(5): 494-498.

WU Kai, ZHU Lin-li. Mechanical Properties of Nanotwinned Metals with Bimodal Twin Spacing Distribution[J]. China Science Paper, 2018, 13(5): 494-498.

[15] 張梓煜, 曾攀, 雷麗萍. 基于機器學習的大鍛件拔長變形預測[J]. 鍛壓技術, 2018, 45(10): 209-216.

ZHANG Zi-yu, ZENG Pan, LEI Li-ping. Prediction of Drawing Deformation for Heavy Forgings Based on Machine Learning[J]. Forging& Stamping Technology, 2018, 45(10): 209-216.

[16] 李志雄, 嚴新平. 獨立分量分析和流形學習在VSC-HVDC系統故障診斷中的應用[J]. 西安交通大學學報, 2011, 45(2): 44-48.

LI Zhi-xiong, YAN Xin-ping. Independent Component Analysis and Manifold Learning with Applications to Fault Diagnosis of VSC-HVDC Systems[J]. Journal of Xi'anJiao Tong University, 2011, 45(2): 44-48.

[17] 馬文博, 梅磊, 劉波. 基于ICS-LSSVM的包裝機械動力機軸承的故障識別[J]. 包裝工程, 2018, 39(11): 176-181.

MA Wen-bo, MEI Lei, LIU Bo. Fault Identification of Power Machine Bearings of Packaging Machinery Based on ICS-LSSVM[J]. Packaging Engineering, 2018, 39(11): 176-181.

[18] 李建明, 楊挺, 王惠棟. 基于深度學習的工業自動化包裝缺陷檢測方法[J]. 包裝工程, 2020, 41(7): 175-184.

LI Jian-ming, YANG Ting, WANG Hui-dong. An Industrial Automation Packaging Defect Detection Method Based on Deep Learning[J]. Packaging Engineering, 2020, 41(7): 175-184.

[19] SHOTARO Minami. Predicting Equity Price with Corporate Action Events Using LSTM-RNN[J]. Journal of Mathematical Finance, 2018, 8(1): 58-63.

[20] SHI Xiu-jin, CAI Yi-fan, YANG Yang. Extreme Trees Network Intrusion Detection Framework Based on Ensemble Learning[C]// Dalian: 2020 IEEE International Conference on Advances in Electrical Engineering and Computer Applications, 2020: 246-255.

Mechanical Properties of Mild Steel Based on Deep Learning

WANG Zheng-huan1a, ZHANG Chao-feng1b, LU Jing1c, LI Wei-li2

(1a.Information Construction and Management Center b. School of Mechanical Engineering c. School of Design, Jiangnan University, Wuxi 214122, China; 2.Wuxi Open University, Wuxi 214011, China)

The work aims to propose an analysis method based on deep learning to predict the mechanical properties of mild steel, in order to analyze the mechanical properties of mild steel under large plastic tensile load in mechanical engineering. Firstly, the tensile experiments were carried out to the mild steel materials with different step angles and the collected experiment data were analyzed by intelligent technology. The experiment model was designed to be a two-layer structure. The first layer was shared full connection layer for feature input. The second layer adopted extreme random tree and long-term and short-term memory network to carry out parallel depth training, and output the training results after activation function calculation. The parallel training model could better reflect the strain and stress change trend, velocity and numerical relationship in the experimental test set. The experimental results showed that the parallel training model could improve the fitting effect by 28.3% and 63.5% respectively compared with the single ET and LSTM prediction technology. Good prediction results can be obtained through the new model, which provides an important reference for the analysis of mechanical properties of mild steel materials in the metal damper under large plastic tensile load.

mechanical design; mechanical properties; machine learning; extreme random trees; long and short term memory

TH122

A

1001-3563(2022)01-0219-09

10.19554/j.cnki.1001-3563.2022.01.028

2021-05-03

江蘇省現代教育技術研究智慧校園專項（2020-R-84358）；全國職業教育教師企業實踐基地“產教融合”專項

王正桓（1977—），男，工程師，主要研究方向為人工智能技術、計算機應用技術。