基于蒙特卡洛方法的可靠性靈敏度分析★

劉曉靜

（山西工程職業(yè)學(xué)院，山西 太原 030009）

引言

可靠性靈敏度分析方法是基于可靠性計(jì)算方法之上的分析方法，是可靠性分析方法的遞進(jìn)。早在1985年HaftkaRT,GurdalZ[1]就對(duì)結(jié)構(gòu)系統(tǒng)的敏感度設(shè)計(jì)進(jìn)行了研究。張義民[2]等提出了單自由度非線性隨機(jī)參數(shù)振動(dòng)系統(tǒng)的可靠性靈敏度分析，討論了隨機(jī)參數(shù)服從正態(tài)分布的機(jī)械結(jié)構(gòu)的可靠性靈敏度設(shè)計(jì)。

建立剛性四桿機(jī)構(gòu)輸出角的模型，采用蒙特卡洛方法對(duì)輸出角的可靠性靈敏度進(jìn)行研究，為后續(xù)有效提高運(yùn)動(dòng)機(jī)構(gòu)的可靠性和穩(wěn)健性打好基礎(chǔ)。

1 Monte Carlo可靠性靈敏度

結(jié)構(gòu)在規(guī)定時(shí)間和規(guī)定條件下完成規(guī)定功能的能力，稱為可靠性[3]。在規(guī)定時(shí)間和規(guī)定條件下完成預(yù)定功能的概率為可靠度。可靠性對(duì)于基本隨機(jī)參數(shù)的偏導(dǎo)數(shù)為可靠性靈敏度。

靈敏度為失效概率pf對(duì)基本變量xi的分布參數(shù)（i=1，2，…，n；k=1，2，…，m），其中mi為第i個(gè)變量xi分布參數(shù)總數(shù)的偏導(dǎo)數(shù)，將失效概率的積分對(duì)分布參數(shù)求導(dǎo)數(shù)，則得到可靠性靈敏度如下[4]：

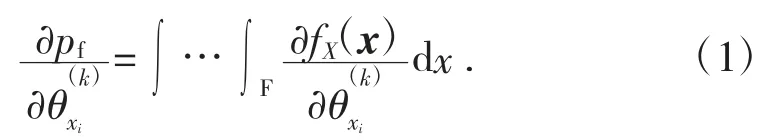
Monte Carlo[5]模擬過(guò)程中，采用樣本均值代替總體均值，數(shù)學(xué)期望可以用樣本函數(shù)的均值來(lái)估計(jì)：

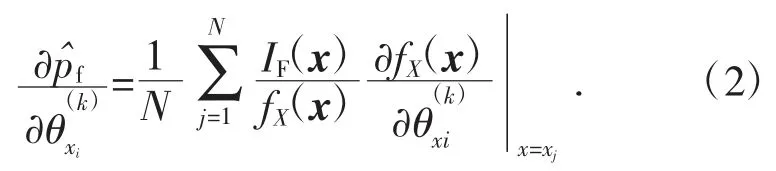
失效概率對(duì)于參數(shù)的無(wú)量綱靈敏度系數(shù)表達(dá)式如下：

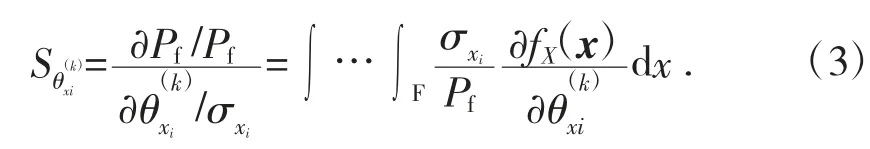
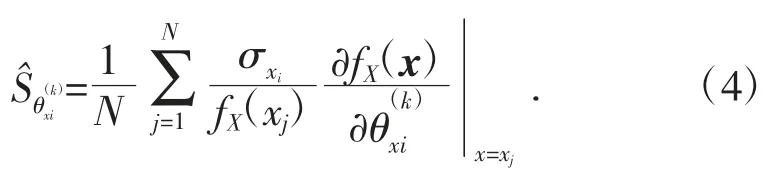
服從正態(tài)分布的變量的失效概率對(duì)于均值和標(biāo)準(zhǔn)差的無(wú)量綱靈敏度系數(shù)[6]如下：

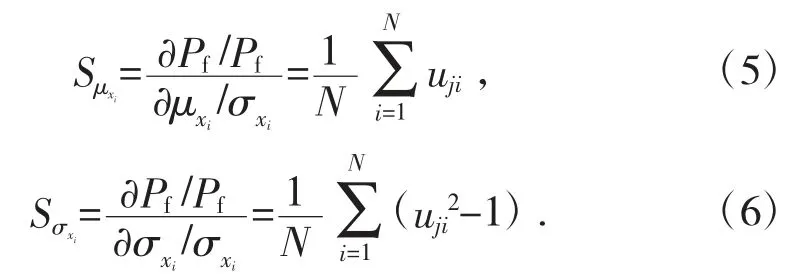
式中，uji為第j個(gè)樣本xj=（xj1，xj2，…，xjn）T的第i個(gè)分量對(duì)應(yīng)的標(biāo)準(zhǔn)正態(tài)變量，即。

系統(tǒng)不能完成規(guī)定功能的概率表示為失效概率pf。系統(tǒng)的可靠度pr與失效概率滿足以下關(guān)系式：

系統(tǒng)可靠性分析的主要問(wèn)題就是處理系統(tǒng)的隨機(jī)問(wèn)題來(lái)確定系統(tǒng)的失效概率。

如果連續(xù)隨機(jī)變量Z的概率密度函數(shù)為fZ（z），則由失效概率的意義可知：

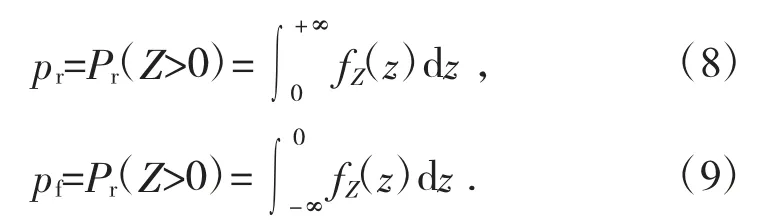
如果用fX（x）=fX（x1，x2，…，xn）表示基本隨機(jī)變量X=（X1，X2，…，Xn）T的聯(lián)合概率密度函數(shù)，用FX（x）=FX（x1，x2，…，xn）表示聯(lián)合累積分布函數(shù)，那么系統(tǒng)的失效概率可表示為：

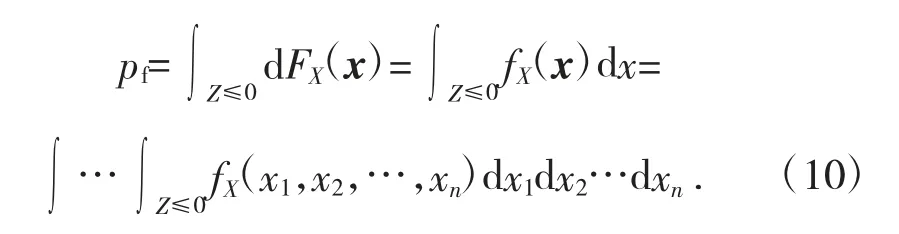
若各基本隨機(jī)變量Xi之間相互獨(dú)立，且Xi的概率密度函數(shù)為fX（ix）i，則失效概率為：

可靠指標(biāo)是可靠性指標(biāo)的簡(jiǎn)稱[5]。由于基本隨機(jī)變量的不確定性，其聯(lián)合概率密度函數(shù)的獲取比價(jià)困難，聯(lián)合概率密度函數(shù)的計(jì)算也非常困難，因此在工程上一般不使用式（11）來(lái)計(jì)算失效概率。根據(jù)可靠性指標(biāo)與失效概率的對(duì)應(yīng)關(guān)系，通過(guò)計(jì)算可靠性指標(biāo)來(lái)確定系統(tǒng)的可靠性。

假設(shè)功能函數(shù)Z~N（μZ，σZ），則功能函數(shù)的概率密度函數(shù)為：

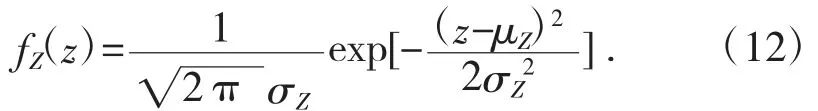
通過(guò)變換，Y=（Z-μZ）/σZ，可以將功能函數(shù)轉(zhuǎn)換成標(biāo)準(zhǔn)正態(tài)分布Y~N（0，1），那么其概率密度函數(shù)和累積分布函數(shù)為：

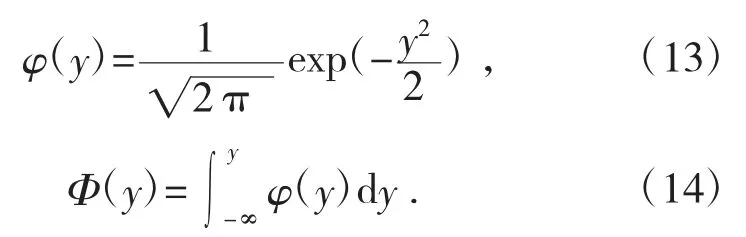
將式（6）代入式（4），并注意到式（7）和式（8），則失效概率[6]為：

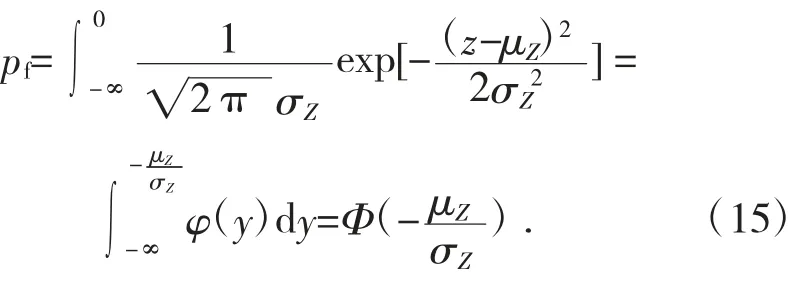
可靠性指標(biāo)、失效概率和可靠概率就可以分別表示為：

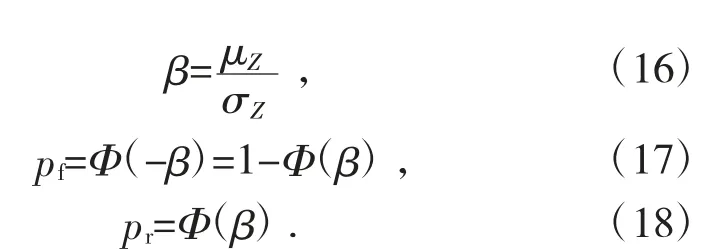
上述對(duì)可靠指標(biāo)的計(jì)算是建立在功能函數(shù)服從正態(tài)分布的條件下。當(dāng)pf≥0.001（或β≤3.090 2）時(shí)，失效概率的計(jì)算結(jié)果能夠滿足工程上所要求的精度，因此可以不考慮基本變量的分布類型而簡(jiǎn)化計(jì)算過(guò)程；當(dāng)失效概率或可靠指標(biāo)不滿足以上關(guān)系時(shí)，必須考慮功能函數(shù)的概率分布形式。

Monte Carlo法計(jì)算求解齒輪接觸疲勞可靠度的大致過(guò)程如下為：由基本隨機(jī)參數(shù)的聯(lián)合概率密度函數(shù)fX（X）模擬產(chǎn)生N組隨機(jī)樣本xj（j=1，2，…，N），把樣本數(shù)據(jù)值代入齒輪接觸疲勞的極限狀態(tài)方程里，然后統(tǒng)計(jì)落入可靠域的樣本點(diǎn)數(shù)，即齒輪傳動(dòng)齒面接觸應(yīng)力小于齒面許用接觸應(yīng)力Nr，用頻率Nr/N近似代替可靠度PR，則

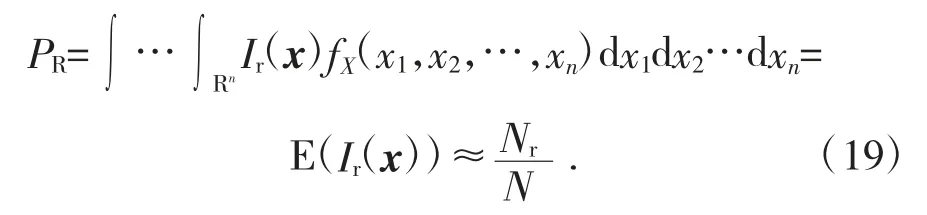
2 算例

圖1為四桿

圖1 四桿機(jī)構(gòu)角度示意圖

機(jī)構(gòu)的角度示意圖，主動(dòng)桿件轉(zhuǎn)速為300 r/min，L1，L2，L3，L4已知，具體值及分布類型見下表1。

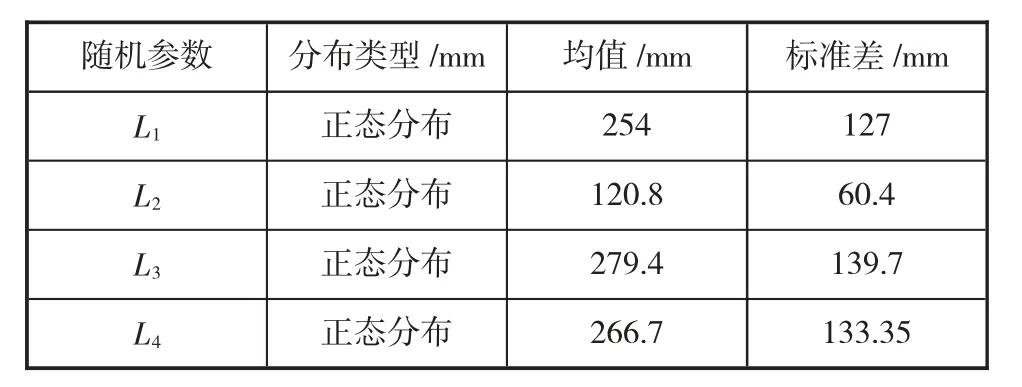
表1 彈性四桿機(jī)構(gòu)的參數(shù)

下頁(yè)圖2為基于蒙特卡洛方法對(duì)四桿機(jī)構(gòu)輸出角可靠性分析流程圖。

根據(jù)表1機(jī)構(gòu)變量參數(shù)表對(duì)參數(shù)抽取106個(gè)樣本點(diǎn)，計(jì)算剛性機(jī)構(gòu)輸出角并進(jìn)行可靠性及靈敏度分析，根據(jù)式（5）和式（6）對(duì)輸出角的失效概率關(guān)于各參數(shù)求均值與標(biāo)準(zhǔn)差靈敏度進(jìn)行求解。

從下頁(yè)圖3、圖4中可以看出，對(duì)于輸出角的失效概率對(duì)于桿件L3的敏感度程度相對(duì)大。可以看出各參數(shù)的均值靈敏度有正值有負(fù)值，說(shuō)明不同參數(shù)的均值對(duì)于輸出角的失效概率影響有正有負(fù)。L3均值靈敏度均為正值，說(shuō)明L3的均值對(duì)于失效概率的影響是積極的。而對(duì)于各參數(shù)的標(biāo)準(zhǔn)差靈敏度則基本為負(fù)值，各參數(shù)標(biāo)準(zhǔn)差對(duì)于失效概率的靈敏度影響是消極的，且L3的標(biāo)準(zhǔn)差對(duì)靈敏度消極影響較其他參數(shù)更大。

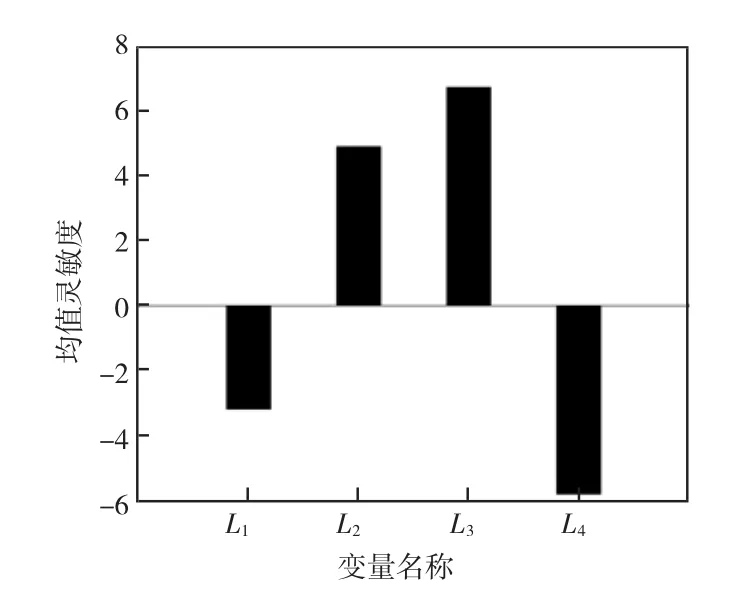
圖3 均值靈敏度直方圖

圖4 標(biāo)準(zhǔn)差靈敏度直方圖

3 結(jié)語(yǔ)

各參數(shù)均值中對(duì)輸出角的影響最大的為L(zhǎng)3，并且是積極影響；各參數(shù)的標(biāo)準(zhǔn)差對(duì)輸出角的影響最大的也為L(zhǎng)3，并且是消極影響。

由此通過(guò)計(jì)算可以得到彈性四桿機(jī)構(gòu)中任意一點(diǎn)處，隨著主動(dòng)桿件轉(zhuǎn)動(dòng)，各參數(shù)對(duì)于輸出角可靠性影響，為后續(xù)有效地提高運(yùn)動(dòng)機(jī)構(gòu)的可靠性和穩(wěn)健性打好基礎(chǔ)。