利用不等式約束求解病態問題的新算法
趙邵杰 宋迎春 李文娜
(1. 中南大學 地球科學與信息物理學院, 湖南 長沙 410083; 2. 有色金屬成礦預測與地質環境監測教育部重點實驗室(中南大學), 湖南 長沙 410083)
0 引言
病態問題是大地測量的數據處理中常出現的棘手的問題,廣泛存在于控制網平差、精密軌道解算、重力場向下延拓、變形監測、極化干涉合成孔徑雷達(Polarimetric Interferometric Synthetic Aperture Radar,PolInSAR)植被參數反演等領域。病態問題法方程的條件數遠大于設計矩陣的條件數,誤差方程系數陣或常數向量的微小擾動,便會造成參數解劇烈變化,難以得到可靠的結果,主要原因是:系數陣出現了相對較小的奇異值,且最大與最小的奇異值相差了幾個甚至十幾個量級,這將導致計算過程中,未知參數的方差被較小奇異值過度放大,顯著降低平差結果的精度[1]。在病態問題的處理上,目前有許多成熟的方法。如:嶺跡法、GCV法(Generalized Cross-Vali-dation)、Tikhonov正則化法[2]、截斷奇異值法[3]等。這些方法在一定的條件下可以降低平差模型的病態性,得到較可靠的平差結果,不足之處在于無法利用測繪工程中的先驗信息。
根據未知參數的先驗信息建立不等式約束,并同誤差方程聯合平差的方法,稱為不等式約束平差法。這種方法補充了平差問題的信息量,對未知參數形成有效約束,深受國內外專家學者的廣泛關注[4-15]。由于不等式約束的存在,它給平差問題的解算帶來了一定的難度,在已有的文獻中,許多學者重點研究了不等式平差模型的解算方法,然而,他們很少或者沒有針對系數矩陣病態問題展開研究。如,在橢球約束算法[15]計算過程中,將不等式約束表示為橢球約束的形式,通過計算廣義型嶺估計得到平差結果,但由于轉化過程會弱化不等式約束的條件,可能導致平差結果不在不等式約束范圍內,從而嚴重影響參數解的精度,故這類方法受主觀條件的影響較大。在有效約束算法[14]和規劃類算法[11]計算過程中就有法矩陣求逆運算,或法矩陣的子矩陣求逆運算。當系數矩陣病態時,這些求逆運算就會出現異常,使得解產生嚴重的偏離。
當不等式約束作為一個先驗信息納入平差運算時,在病態的平差模型中可以增加一些虛擬的觀測信息,這顯然可以對觀測信息進行補充,從而降低平差模型的病態性,使得平差結果更加可靠。這需要在構建不等式約束平差算法時,盡量避免對病態系數矩陣進行求逆運算,否則不等式約束信息還沒有利用,其病態問題的影響已經在參數解中存在了。因此,避免對病態矩陣求逆是求解病態問題的一個較理想的途徑。
本文針對未知參數具有不等式約束的情形,通過KKT(Karush-Kuhn-Tucker)條件將平差問題轉化為線性互補問題(Linear Complementary Problem,LCP)[16-18],轉換后的LCP的系數矩陣是非對稱的、病態的,現有的平差算法無能為力。本文借助Lemke算法給出了針對非對稱的、病態的LCP的一個算法,同時,為利用Lemke算法解決不等式約束平差問題提供了一個新的途徑。新的算法不同于已有的不等式約束算法,在算法構建過程中完全避免了矩陣求逆運算,使得病態性在計算過程中對迭代解的影響大大降低。論文通過幾個實例驗證了算法在處理病態問題的有效性,豐富了利用不等式約束解決病態問題的算法。
1 病態性影響分析
平差模型
L=AX+e權陣P
(1)
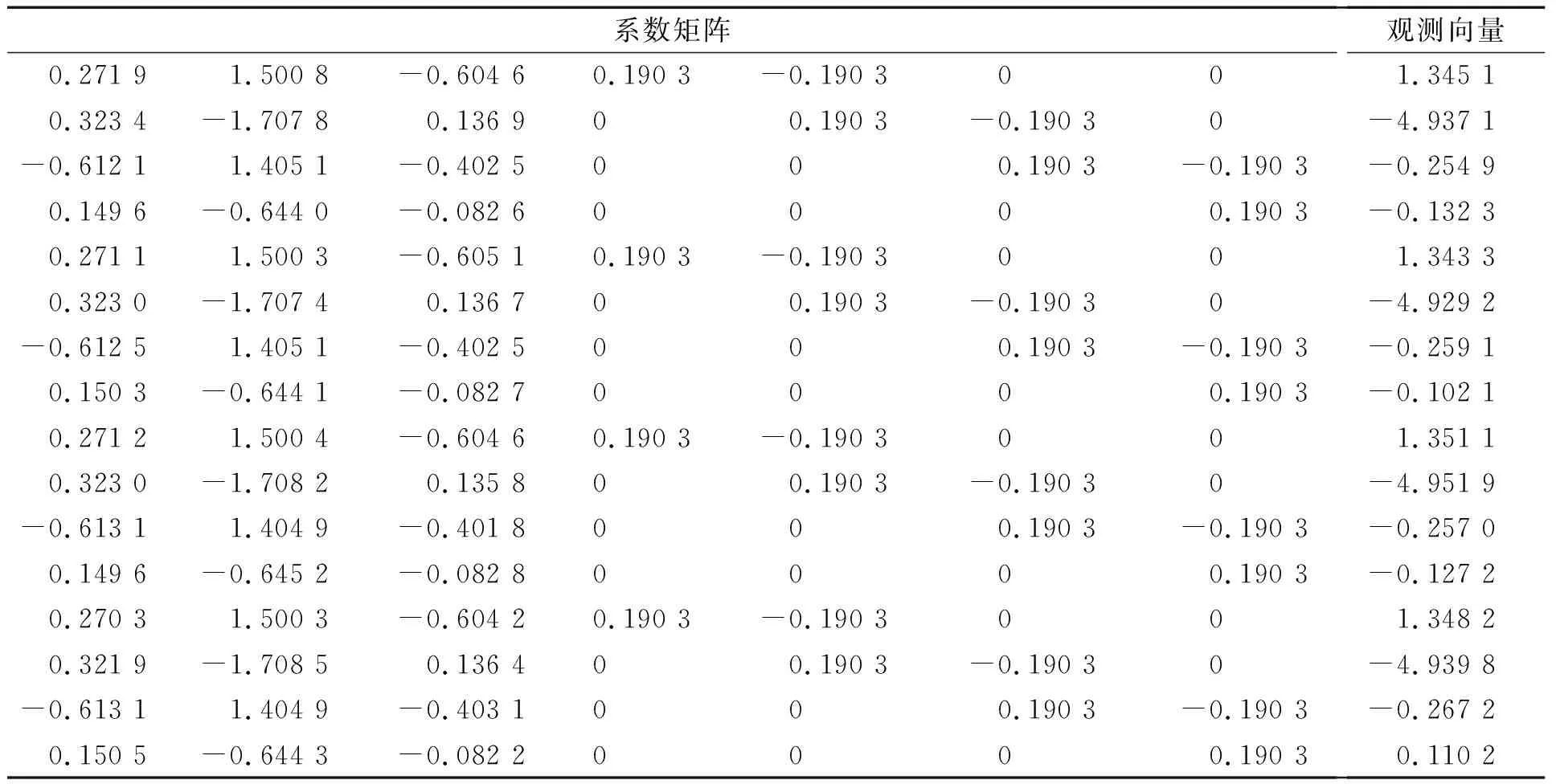
其中,A是m×n維的列滿秩矩陣,rank(A) min ‖L-AX‖2 (2) 式(2)中,‖·‖2表示2范數。式(2)稱為病態問題,在矩陣A無病態條件下,最小二乘解為 (3) 我們對病態問題的系數陣A進行奇異值分解 (4) (5) 其中,UA=[u1,…,um]是m階的正交矩陣;GA=[g1,…,gn]是n階的正交矩陣;n×n維的對角陣Σ=diag(λ1,λ2,…,λn),對角線元素為A的奇異值,且λ1≥λ2≥…≥λn≥0。 由于系數陣A病態,我們設λN1、λNn為法方程系數陣N=ATPA的最大奇異值、最小奇異值,則法方程系數陣的條件數為 (6) 統計應用經驗表明,法方程條件數小于100時可以認為沒有病態性;條件數位于100到1 000之間認為存在中等程度的病態性;條件數大于1 000認為存在嚴重的病態性[19]。若條件數cond(N)很大,即使N和L的擾動很小,求解式(3)時也會引起X很大的偏差。因此,改善病態問題的一個可行途徑,就是避免對法方程中的不穩定(條件數很大)矩陣N求逆,增強解的抗干擾能力。 目前,病態問題的研究主要在兩個方面,一是對平差模型進行診斷,判斷是否病態;另一方面是研究病態問題的解算方法,例如:正則化方法,截斷/修正奇異值方法。附加約束方法等確定性方法和隨機方法。下面,我們將對求解病態問題的新算法進行研究。 最小二乘平差準則為 minf(X)=(L-AX)TP(L-AX) (7) 因在目標函數(L-AX)TP(L-AX)=XT(ATPA)X-2LTPAX+LTPL,LTPL是一個常量,故可以把式(6)轉化為一個二次規劃問題 (8) 式(7)中,c=-(LTPA)T為n維的列向量,N=ATPA為n×n維的對稱正定矩陣,故f(X)是嚴格凸二次函數,即f(X)的局部最小值為全局最小值。我們將先驗信息表示為不等式約束GX≤h,X≥0,其中,G為s×n維的行滿秩矩陣,h為s維的列向量,并聯合式(1),得到具有不等式約束的病態模型 L=AX+e權陣P (9) s.tGX≤h,X≥0 (10) 此處,沒有把式(10)中的兩個不等式合成一個不等式,是為了便于式(8)和(9)的轉換。由上面的分析可知式(8)和(9)可轉換為如下的二次規劃問題(Quadratic Programming): (11) s.tGX≤h,X≥0 (12) 二次規劃問題是非線性規劃中一種特殊的情形,典型的算法有:Lagrange方法、起作用集方法、路徑跟蹤法、Wolfe算法等[22-23]。前三種方法無法回避對病態矩陣求逆,Wolfe算法應用廣泛,卻要求N半正定,故不適用于常規的病態問題。因此,尋找一種不求逆的、大多數情況適用的解算方法是很有必要的[20],由于Lemke算法既可避免對病態矩陣求逆,又可處理N正定和半正定情形,故本文深入研究了這種方法在病態問題中的應用。 本文利用不等式約束求解病態問題,需將已得到的二次規劃問題轉化為LCP,再結合Lemke算法求解。由于A列滿秩,其法方程系數陣N是一個正定矩陣,f(X)為嚴格凸二次函數,故函數的局部最小值也是全局最小值,K-T點是式(10)和(11)的最優解。根據Karush-Kuhn-Tucker條件 NX+GTY+c-u=0,v=h-GX≥0 (13) vTY=0,uTX=0 (14) u≥0,v≥0,X≥0,Y≥0 (15) 式(10)整理得 (16) (17) MZ+q≥0,Z≥0,ZT(MZ+q)=0 (18) 其中,M∈R(s+n)×(s+n)是非對稱矩陣;q∈Rs+n;Z∈Rs+n。 式(9)到式(18)的推導,目的是把不等式約束條件下的病態模型轉化為線性互補問題求解。式(18)的等價形式為 w-MZ=q,w≥0,Z≥0,wTZ=0 (19) 由于M是非對稱的、病態的矩陣,利用一般的線性互補問題算法是不能求解式(18)的。對于式(19)需要研究特殊情形的線性互補問題,如非對稱LCP,秩虧LCP等,因此,這些算法直接移植到測量平差中來是非常復雜的,從式(16)和(17)可以看出,w和Z不僅要滿足m+n維未知變量的線性方程組,而且要保證wTZ的內積為零。1962年,Lemke基于單純型算法的思想,提出了求解線性互補問題式(19)的Lemke算法。這種算法建立在表1的基礎上,可用于處理非對稱的LCP,輸出的結果完全符合式(19)解的性質。由于表1中只含有一個線性方程組的系數矩陣,沒有對應目標函數的系數向量,故它在結構上比線性單純形表的設計更為簡單。下面,給出了該算法的具體步驟[24]。 表1 線性互補問題對應的單純形表 第1步將線性互補問題的系數陣M和向量q寫入一個單純形表中。若單純形表的最右列q的分量非負,即q≥0,停止計算。否則,添加人工變量z0,使之對應的系數為-1,并將該列寫于q的左邊一列。 第2步將q中對應負數絕對值最大的元素所在的行作為主行,選取z0中主行上的元素作為 主元消去的元素,進行主元消去,并記錄此時w出基變量的序號。 第3步設出基變量為ws(或zs),則要求下一次必須zs(或ws)將作為進基變量。主元消去元素應在該列中選取,其對應的主行r應滿足: (20) 其中,dj為當前表中即將進基變量所在列對應的第j個分量;pj為當前單純形表最右列q對應的第j個分量。 第4步進行主元消去,若此時人工變量z0出基,轉第6步;否則,第5步。 第5步記錄主元消去的出基變量的序號,轉第3步。 第6步輸出對應的最優的平差結果Z=(X,Y)T。 算法步驟分析,以下面方程組為例 (21) 算法示意圖分析: 圖1(a)→(b)為第1步至第2步的過程:建立Lemke算法表,首先根據q的負數絕對值最大的元素“-10”確定z0列的主行元素w2,接著w2出基z0進基,并進行主元消去。根據式(14)定位第3步將主元消去的位置,即(w1,z2)。 圖1(c)→(d)為第3步至第6步的過程:在對(w1,z2)進行主元消去后,w1出基z2進基,我們發現z0并未出基,故根據式(20)重新定位第3步主元消去的位置(w3,z1),進行主元消去,w3出基z1進基。接著重復第3步定位主元消去的位置,完成進基、出基的過程,直至z0出基,圖1(d)展示了算法結束時的狀態。根據Lemke算法表,我們得到了LCP的互補可行解 (22) 圖1 Lemke算法示意圖 由于Lemke算法應用不等式約束解病態問題過程,并未涉及到對病態矩陣的求逆運算,故平差結果不會受到病態矩陣求逆的影響,保證了未知參數X的穩定性;在二次規劃式(13)中,法方程系數陣N是正定矩陣,二次規劃為嚴格的凸二次規劃,因此,保證了未知參數X的唯一性[20]。綜合未知參數具有穩定性和唯一性的特點可知,用Lemke算法求解不等式約束病態問題是一種理論清晰、目的明確的新方式。嶺跡法、GCV法、L-曲線法等是大地測量數據處理中,使用頻率很高的處理病態問題的算法,但它們無法回避對病態矩陣的求逆,嶺估計方法雖然可以應用到病態矩陣的求逆問題,但嶺參數的確定方法是人為的方法,無法利用未知參數X的先驗信息,因此,存在著局限性。Lemke已在測繪數據處理中得到應用[11],這些應用主要還是針對不等式約束的算法研究,而不是針對病態問題進行研究。下面,結合兩個模擬算例進行實驗分析,驗證Lemke算法的有效性。 Hilbert矩陣是經典的病態矩陣,定義為 (23) (24) 圖3 L-曲線法示意圖 圖4 嶺跡法示意圖 從平差結果可以看出,由于系數矩陣的高度病態性,使得最小二乘解XLS嚴重失真,‖XLS-Xreal‖的值高達3.418 3×1011;方法1和方法2雖然利用了未知參數X的先驗信息GX≤W,在一定程度上提高了解的精度,卻未能改變平差模型AX=L的病態性,因此,平差的結果也嚴重失真。 表2 幾種算法的平差結果比較 根據GX≤h,X≥0,將先驗信息Δx≤2.3 m,Δy≤4.0 m,Δz≤6.8 m,表示為不等式 表3 系數矩陣和觀測向量 單位:m 表4 GPS快速定位的算法結果與比較 單位:m (25) 從表4的平差結果,可以得出以下的結論: (1)在本算例中,法方程的條件數為cond(N)=2.480 9×109,因此,法方程嚴重病態。此情況下,按最小二乘的準則對法方程進行求逆運算,必然會導致未知參數的解不穩定,實驗結果也驗證了最小二乘解嚴重偏離未知參數的真值。 (2)GCV法、L-曲線法、嶺跡法均未利用到未知參數的先驗信息,故未得到理想的平差結果。嶺跡法相對于其他兩種方法,偏離真值的程度要大得多,一方面與嶺參數在選擇上受主觀意識影響較大有關,另一方面也與數據結構有關。對于不同的數據,嶺估計對病態問題的改善程度也是不同的。 (3)方法1和方法2屬于廣義型嶺估計,具有一定的主觀性。從平差結果可以看出這兩種方法均未克服法方程的病態性,方法2在觀測數據和約束條件理想的條件下,也可以在一定程度上對參數解改善。 (4)本文提出的不等式約束病態平差模型的Lemke算法充分利用了先驗信息,對未知參數形成了有效約束,平差結果同真值最為接近且效果最好,顯示出了這種算法的優越性。 大地測量中,未知參數的先驗信息反映了被測目標的幾何或物理特征、內在相關性、測量精度等,在數據處理中,結合有效的先驗信息以等式或不等式約束的形式進行平差,可以補充觀測信息的不足,對未知參數形成約束,有效提高參數估計的效率。本文針對病態問題,提供了一種新的平差方法——Lemke算法。本算法沒有涉及病態矩陣N=ATPA的求逆,因此,A的病態性對Lemke算法影響不大,有效抑制系數矩陣的復共線性,降低解的不穩定性。其次,Lemke算法在構造上簡明易懂,充分利用測繪工程中的先驗信息解決病態問題,降低了平差模型的復雜性,豐富了病態問題的算法理論。2 不等式約束病態模型與Lemke算法
2.1 不等式約束病態模型
2.2 線性互補在平差問題中的應用
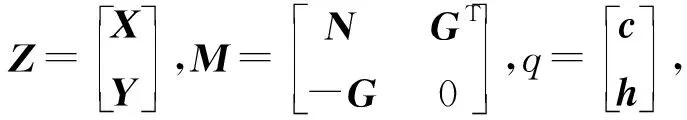

2.3 Lemke算法步驟
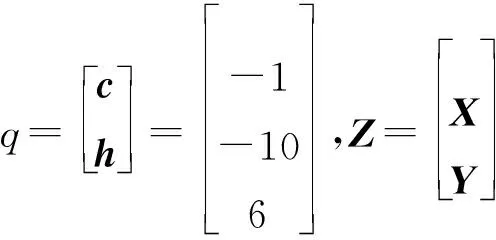
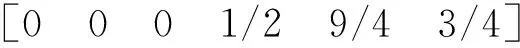

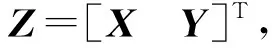
3 算例1






4 算例2



5 結束語

