Saturation number of strong bipartite hypergraphs

Gu Ran,Shi Yongtang

(1.College of Science,Hohai University,Nanjing 210098,China;2.Center for Combinatorics and LPMC,Nankai University,Tianjin 300071,China)

Abstract：Given an r-graph F,an r-graph G is F-saturated if G is F-free but adding any new edge e to G creates a copy of F for every r-edge e∈E(())where() denotes the complement of G.For an r-graph F,the saturation function satr(n,F)is the minimum number of edges that an F-saturated graph on n vertices can have.Let Sr?,mhave ?+m vertices and consist of all edges intersecting some fixed ?-set of vertices.A conjecture on the asymptotic value of satr(n,Sr?,m)was proposed in 2004.In this paper,we prove bounds for satr(n,Sr?,m).

Keywords：saturation,hypergraph,extremal problem

1 Introduction

An r-graph G is a pair(V(G),E(G)),where the edge set E(G)is a family of r-subsets of the vertex set V(G).Given an r-graph F,we say that the r-graph G is F-free if G has no subgraph isomorphic to F.We say an r-graph G is F-saturated if G is F-free but adding any new edge e to G creates a copy of F for every r-edge e∈E(),where() denotes the complement of G.For example,any complete bipartite graph is a K3-saturated graph.

For an r-graph,the saturation number,denoted by satr(n,F),is the minimum number of edges that an F-saturated graph on n vertices can have.We write sat(n,F)instead of satr(n,F)when r=2.The saturation number can be viewed as the dual function of the celebrated Tur′an number ex(n,F),the maximum number of edges in an F-saturated graph of order n.Actually,the Tu′ran problem and Ramsey problem of hypergraphs[1-3]and infinite hypergraphs[4]are widely studied recently.In this paper,we will pay our attention on saturation number of hypergraphs.

The structure and extremal properties of clique-saturated graphs were studied already in Reference[5].The saturation problem for clique Kkwas completely solved in Reference[6],which was used to prove a conjecture of Erd?os and Gallai in Reference[7].

Reference[8]determined the best known general upper bound for sat(n,F).Note that α(F)is the independence number of F and a star on n vertices refers to the complete bipartite graph K1,n-1.To state their result,first define

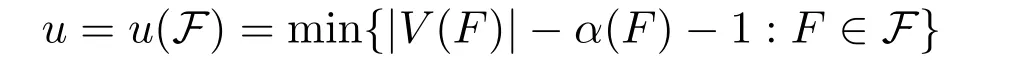
and

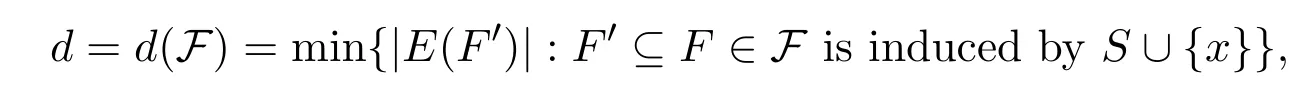
where S is an independent set in V(F)and|S|={|V(F)|-u-1,x∈V(F)S}.Reference[8]proved that

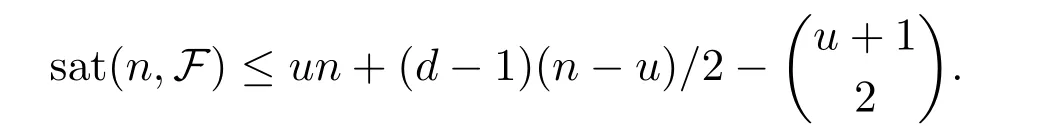
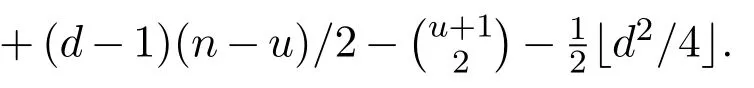
1.1 Saturated numbers on hypergraphs

We now consider F-saturated hypergraphs where F is an r-graph for r≥3.There are not so many results on saturation numbers of hypergraphs.Some known results are listed as follows.

1.1.1 Generalization of complete graph

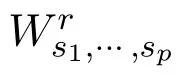
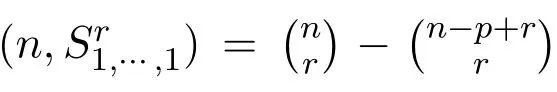
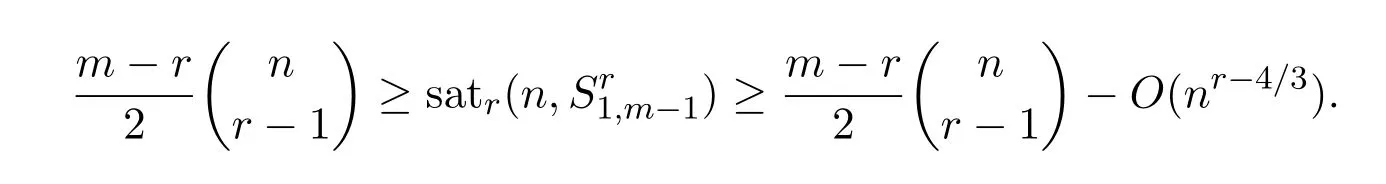
Then Reference[21]posed the following conjecture.

Conjecture 1.1For positive integers ?,m,r with r ≥ 3 and ?+m ＞ r,

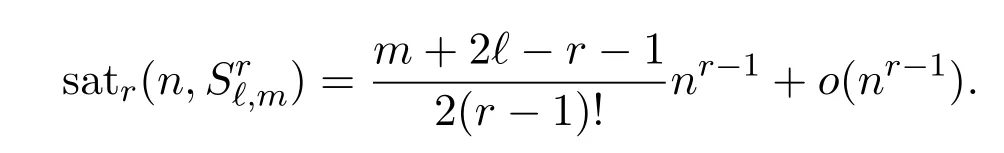
In this paper,we prove bounds for satr(n,Sr?,m).

1.1.2 Berge hypergraphs

A hypergraph H is called a Berge copy of a graph F(in short:H is a Berge-F)if V(F)?V(H)and there is a bijection f:E(F)→E(H)such that for any e∈E(F)we have e?f(e).

Berge hypergraphs were introduced[22].Reference[23]considered the saturation problem for Berge hypergraphs.They conjectured that satr(n,Berge-F)=O(n)holds for any r and F,and proved it for several classes of graphs.The conjecture was proved for 3≤r≤5 and any F in Reference[24].

Reference[24]extended this conjecture to hypergraph-based Berge hypergraphs.Analogously to the graph-based case,a hypergraph H is a Berge copy of a hypergraph F(in short:H is a Berge-F)if V(F)?V(H)and there is a bijection f:E(F)→E(H)such that for any e∈E(F)we have e?f(e).The conjecture in this case states that if F is a u-uniform hypergraph,then satr(n,F)=O(nu-1).

There are some known saturation numbers for some special Berge hypergraphs.Exact saturation numbers for Berge-matching,Berge-triangle and Berge-K1,k+1are obtained in Reference[23],and also the bounds for Berge-cycle,Berge-path and Bergestar.

1.1.3 Some specific hypergraphs

Triangular family:Let Trdenote the family which consists of all r-graphs with three edges E1,E2,E3such that E1△E2? E3,where△ denotes the symmetric difference.We call Tra triangular family.Reference[21]proved that the following theorem.

Theorem 1.1Let r≥3 be fixed.Then

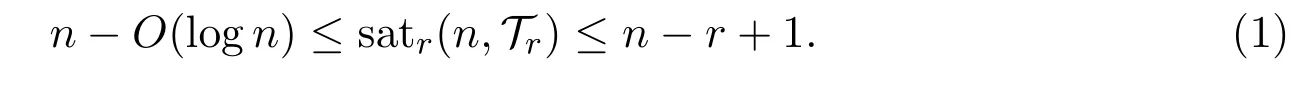
And,for r=3 equality holds on the right.

Reference[21]conjectured the right side of(1)holds for all r≥3.

Disjoint-union-free:An r-graph F on[n]is disjoint-union-free(DUF)if all disjoint pairs of edges of F have distinct unions;that is,if for all E1,E2,E3,E4∈E(F),E1∩E2=E3∩E4=? and E1∪E2=E3∪E4implies that{E1,E2}={E3,E4}.Let F be DUF with the property that F∪{E′}is not DUF for any r-subset E′/∈E(F).Then F is maximally DUF.The problem of finding the minimum size of maximally DUF was considered[25],which proved that for r=3,the minimum size of maximally DUF is n2/12+O(n).It is interesting to consider the problem for r＞3.

1.2 Our results

Theorem 1.2For positive integers ?,m,r with r ≥ 3 and ?+m ＞ r,

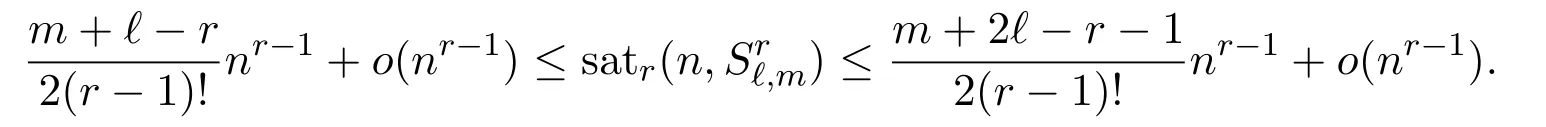
We present the proof in the next section.

2 Proof of Theorem 1.2

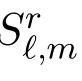
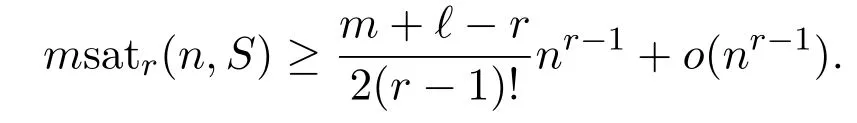
Our technique is similar to what Pikhurko used in Reference[20].

Let G be a minimum monotonically S-saturated r-graph on[n].By the definition,adding any edge F∈E(())creates at least one copy of S.Let S(F)be the set of all such subgraphs S′created by F,where S′is a copy of S.Let F(F)denote the set of edges in G which intersect F∈E(G)in r-1 vertices and create a copy of S containing F as an edge.In other words,

F(F)={F′∈E(()):|F∩F′|=r-1,?S′∈S(F′),F∈E(S′)},F∈E(G).

Further,define

For an r-graph H on[n],let

Since G is monotonically S-saturated we have that

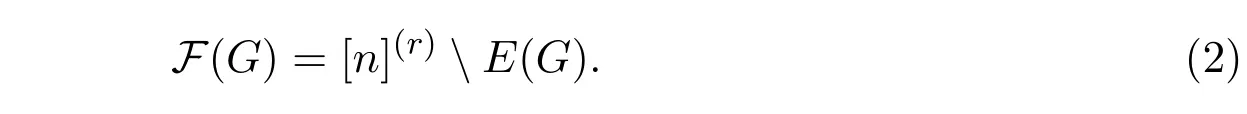
Let k= 「n1/3」.We define two subgraphs G0,G1? G such that G0is a maximal subgraph of G with|F(G0)|≤k|E(G0)|and G1consists of the edges of G not in G0.

By the maximality of G0,for every F∈E(G1)we have

By the upper bound in Theorem 1.2,we know that G has O(nr-1)edges.Then from(2),we obtain that

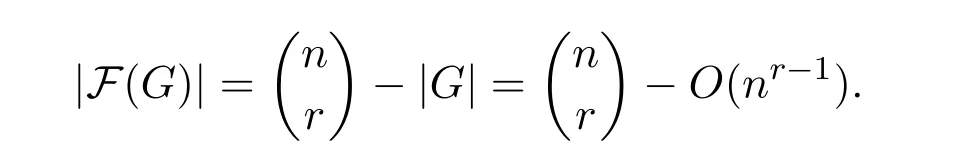
Let X=F(G1)F(G0).Notice that

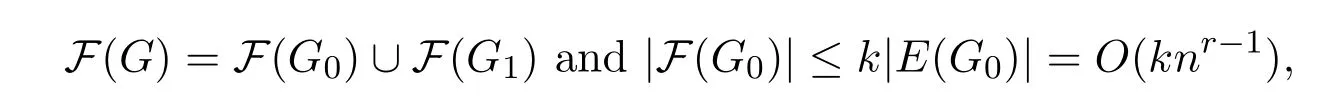
we conclude that

Let Z=[n](r-1)?G1.We have the following claim on the size of Z.Claim 2.1ProofSuppose on the contrary,|Z|O(k1/2nr-3/2).Let

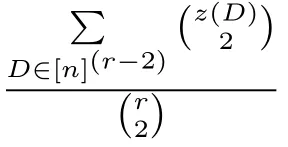
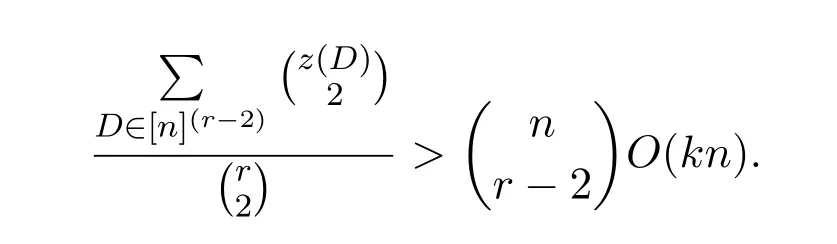
That contradicts(4),and we proved Claim 2.1.

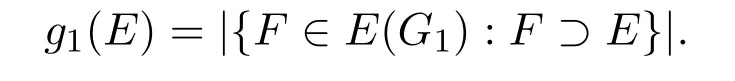
For every E ∈ ?G1,let Now select any F ∈ E(G1).Let ?F={E1,···,Er}.

Claim 2.2Among E1,···,Er,there are at most two of g1(Ei)′s satisfying that g1(Ei)≤k/6.

ProofSuppose on the contrary there are at least three g1(Ei)′s are at most k/6.Assume without loss of generality that

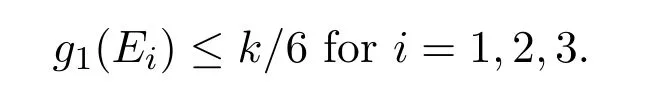
Take F′∈ F(F)F(G0)and any S′∈ S(F′)containing F as an edge.Choose a vertex x ∈ [n]F,let F′=Ei∪{x},for some i∈ [r].The star S′contains r-2 edges of the form Ej∪{x},ji.Note that these edges cannot belong to G0and therefore contribute at least 1 to g1(E1)+g1(E2)+g1(E3).In total,each{x}∪Ej∈E(G1)is counted at most twice,and realize that if some{x}∪Ej∈ E(G1)is counted twice,then at most 2 edges of the form{x}∪Eqcan belong to E(G).Therefore,g1(E1)+g1(E2)+g1(E3)≤k/2 implies|F(F)F(G0)|≤k.Thus,we obtain a contradiction to(3).The claim is proved.

Now consider the following two sets:

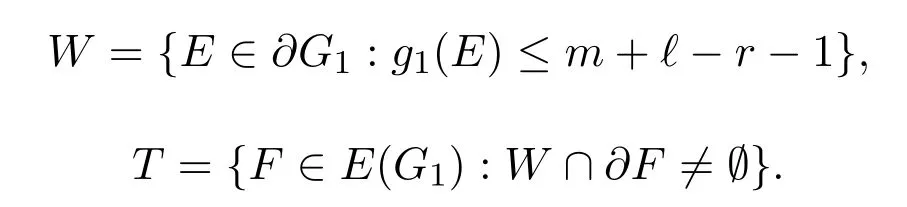
Claim 2.3|W|=O(k1/2nr-3/2).

ProofSuppose|W|O(k1/2nr-3/2).For E,E′∈ W with|E ∩ E′|=r-2,let F=E∪E′.If F/∈X,we let S′∈S(F),then at least one of E,E′has a centre vertex of S′.Suppose without loss of generality that x ∈ E,where x is a centre vertex of S′.So there are m+?-r edges different from F and covering E.And these m+?-r edges belong to E(G1)by the definition of G1.It contradicts the definition of W.Hence F∈X.For D∈[n](r-2),let w(D)=|{E∈W:E?D}|.We obtain that there are at leastedges not in X.Using the convexity of the-function as before,we can obtain that there are more than O(knr-1)edges not in X,which contradicts(4).The claim is established.

Note that every E∈W is contained in at most m+?-r-1 edges F∈E(G1),so|T|=O(k1/2nr-3/2).By Claim 2.2,for every F∈E(G1)T we have

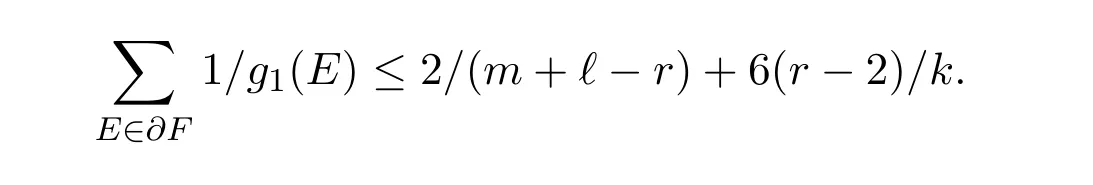
Hence,

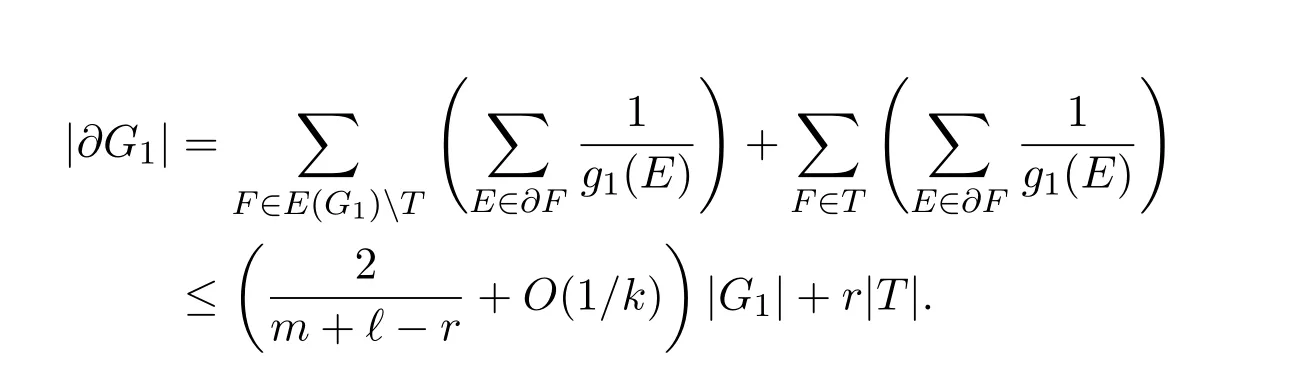
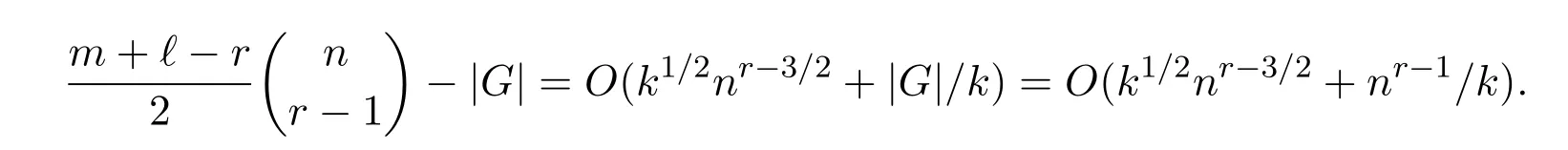
Thus we obtain the desired lower bound.