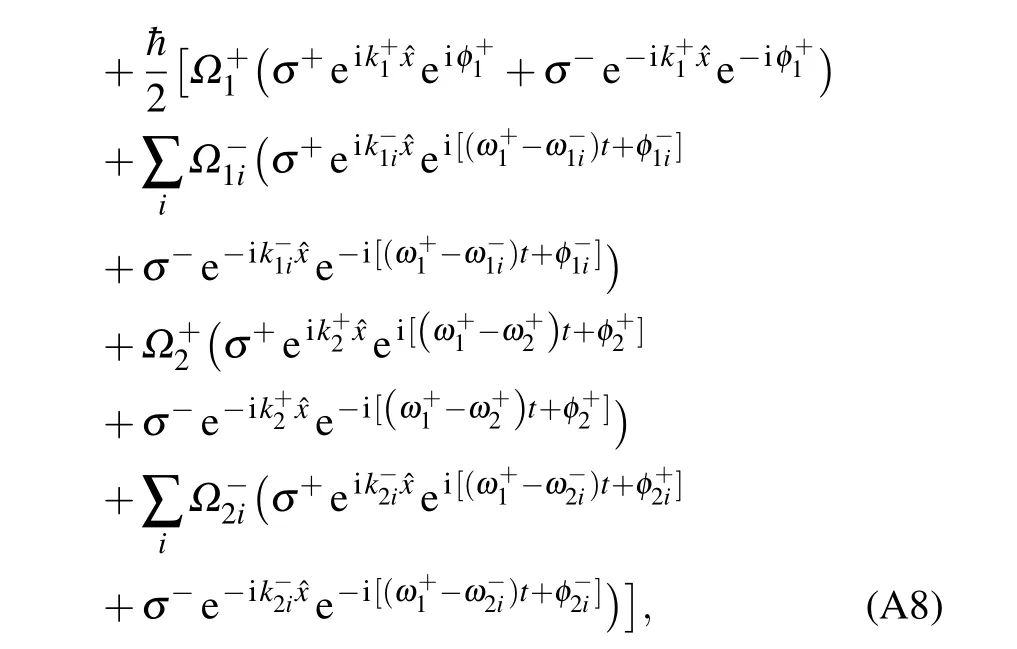Topological phases and type-II edge state in two-leg-coupled Su–Schrieffer–Heeger chains

Tianqi Luo(羅天琦) Xin Guan(關欣) Jingtao Fan(樊景濤)Gang Chen(陳剛) and Suo-Tang Jia(賈鎖堂)

1State Key Laboratory of Quantum Optics and Quantum Optics Devices,Institute of Laser Spectroscopy,Shanxi University,Taiyuan 030006,China

2Collaborative Innovation Center of Extreme Optics,Shanxi University,Taiyuan 030006,China

3Taiyuan Institute,Taiyuan University,Taiyuan 030006,China

4Collaborative Innovation Center of Light Manipulations and Applications,

Shandong Normal University,Jinan 250358,China

Keywords: topological quantum states,edge state,momentum-space lattice

1. Introduction

Since the topological aspect of the quantum Hall effect is revealed,[1-3]a phase transition mechanism beyond Ginzburg-Landau paradigm is being gradually established. Topological quantum states have attracted great attention due to their robustness against various disorders. Lots of topological phenomena have been explored, such as topological insulators(TIs),[4-8]topological semimetals,[9-12]high-order TIs,[13-15]topological Anderson insulators,[16-18]and non-Hermitian skin effect.[19-22]Many of these phenomena have been observed through different platforms, such as cold atom,[23-25]solid,[26,27]photonic crystal,[28,29]phononic crystal,[30-33]and superconducting circuits.[34-36]

Momentum-space lattice provides a powerful tool to study various interesting physical phenomena. It has been shown that two different mechanisms, a quantum version[37]and a classical version,[38]can be used to achieve the momentum-space lattice. The quantum one applies the socalled superradiance lattice,[39-41]in which the optical field couples different spin-wave states, known as timed-Dicke states,[42]to form a tight-binding model, by switching the phase-correlation wave vector discretely. The other mechanism,namely,the classical version,utilizes the classical interaction between light field and atoms. Under this paradigm,the recoil momentum of atoms becomes discrete,which offers opportunity to simulate lattice sites in solid systems.[43-45]The latter owns a unique advantage that the boundaries of the lattices can be unambiguously determined. As such,it is preferable to use the classical version when focusing on physics confined on edges.

In this paper, we propose a two-leg-coupled Su-Schrieffer-Heeger (SSH) model by using the classical momentum-space lattice. By calculating the energy band and winding number, we obtain the topological phase diagram.It is found that the topological edge states occupy two sublattices at the same time, which can be regarded as a onedimension analogue of the type-II corner state.[46]Then, we further demonstrate the existence of the type-II edge state by solving the eigenequations. Finally,the experimental schemes for the topological winding number and corresponding edge states detections based on current experimental setups are proposed.

2. Model and Hamiltonian

We consider a system of two-level ultracold atoms interacting with Bragg laser beams as shown in Fig. 1. Two of these lasers propagate rightward and carry wave numbersk1andk2(k1/k2is irrational),respectively. The lasers propagating leftward can be sorted as two classes:the beams with wave numberk1and the others with wave numberk2. The leftward propagating lasers characterized byk1(k2) are composed of

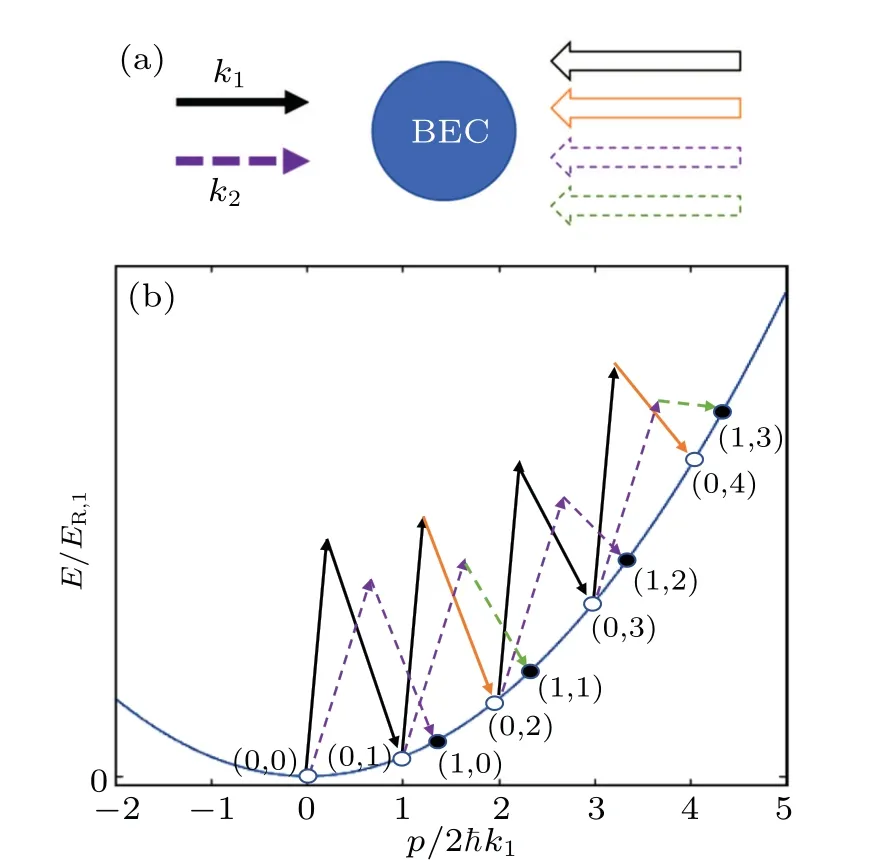
Fig.1. (a)Sketch of the proposed experimental setup. The counterpropagating lasers form a set of Raman structures inducing transitions between different momentum states. The solid and dotted lines represent the laser fields with wave numbers k1 and k2,respectively. Different colors represent different Rabi frequencies. (b)Free-particle dispersion relation and recoil energy ER,1=ˉh2k2/2M. The open and filled circles represent the momentum states in legs n=0 and n=1,respectively. The intraleg and interleg transitions are controlled by lasers with wave numbers k1 and k2,respectively.

where the field operator ?αj,n(?α?j,n)annihilate(create)a particle at sublatticeα(=a,b)of then-th leg andj-th unit cell.The intraleg(interleg)hopping strengths are denoted byvandw(t1andt2). The Hamiltonian(2)describes two-leg-coupled SSH chains with staggered interleg hoppings and opposite dimerizations. The system respects a glide reflection symmetry and a mirror symmetry fort1=t2.[47,48]We sett1=1 as the unit of energy hereafter.

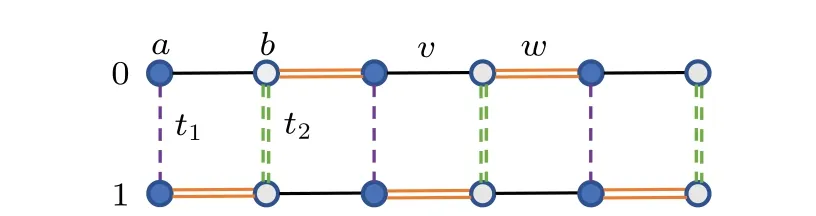
Fig. 2. Sketch of the tight-binding model. The model consists of two legs n=0 and 1, each of which constitutes a SSH type chain. t1 and t2 are the staggered interleg hoppings. v and w are the intracell and intercell hoppings within one leg.

3. Energy spectrum and winding number

Here T is a transport operator.

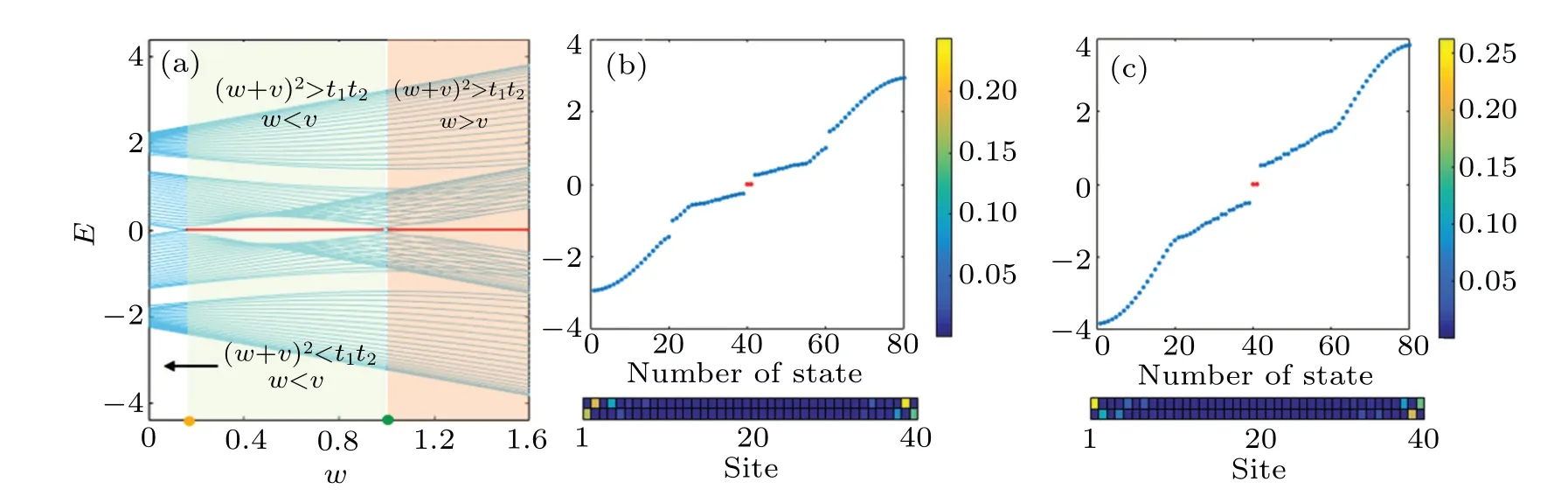
Fig. 3. (a) Energy spectrum of the two-leg-coupled SSH model under open boundary condition with 20 unit cells, the other parameters are v=1 and t2 =1.4. The red line denotes the zero-energy mode. The yellow and green dots are the points where the band gap closes(w=√t1t2-v ≈0.18 and w=v=1). The top panels of(b)and(c)are the eigenenergy with w=0.6 and w=1.6,respectively. The bottom panels of(b)and(c)depict the density population of the edge states with w=0.6 and w=1.6,respectively.

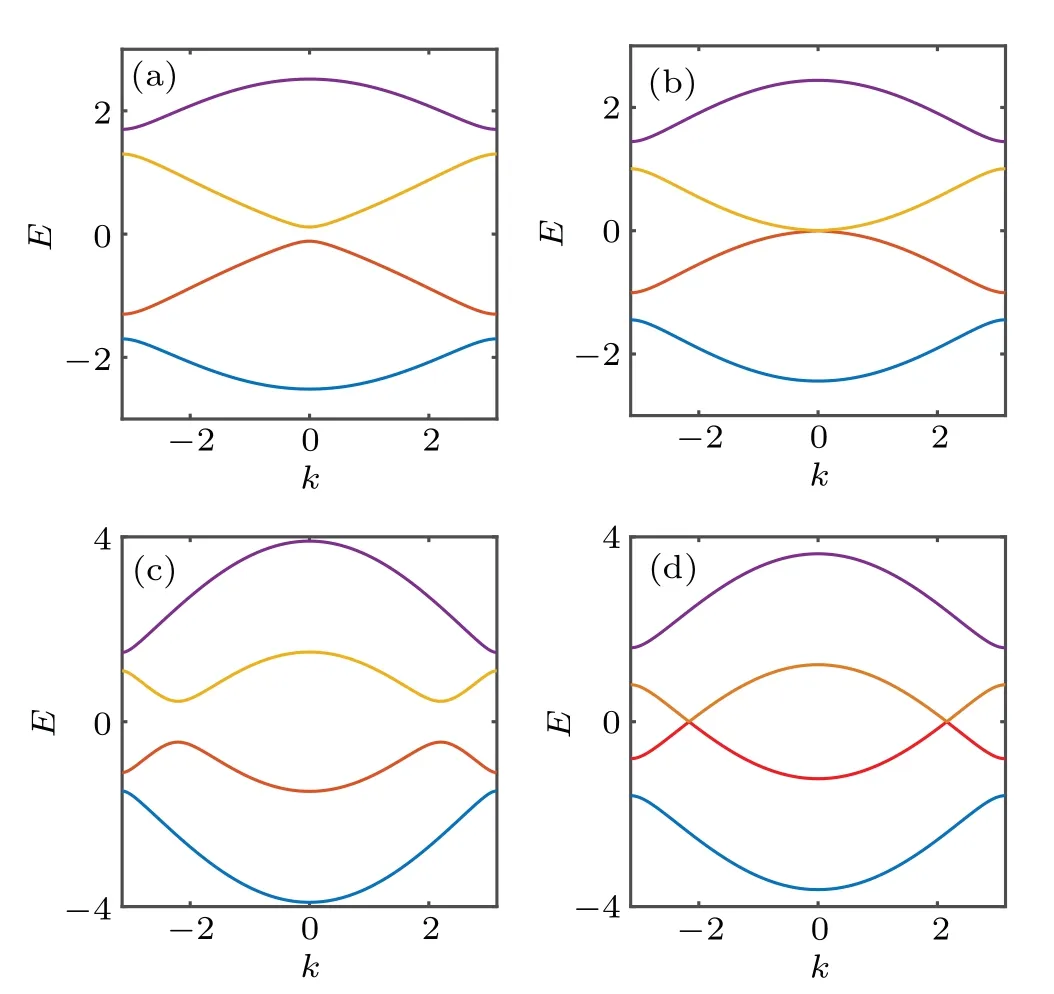
Fig. 4. Plots of the energy band under periodic boundary condition with t2 =1.4, v=0.8 and (a) w=0.1, (b) w=0.4, (c) w=0.6 and(d) w=0.8. (a) and (c), both with a nonzero band gap, correspond to topological trivial and non-trivial cases, respectively; (b)and(d)show a gapless band structure,signaling the appearance of topological phase boundary.

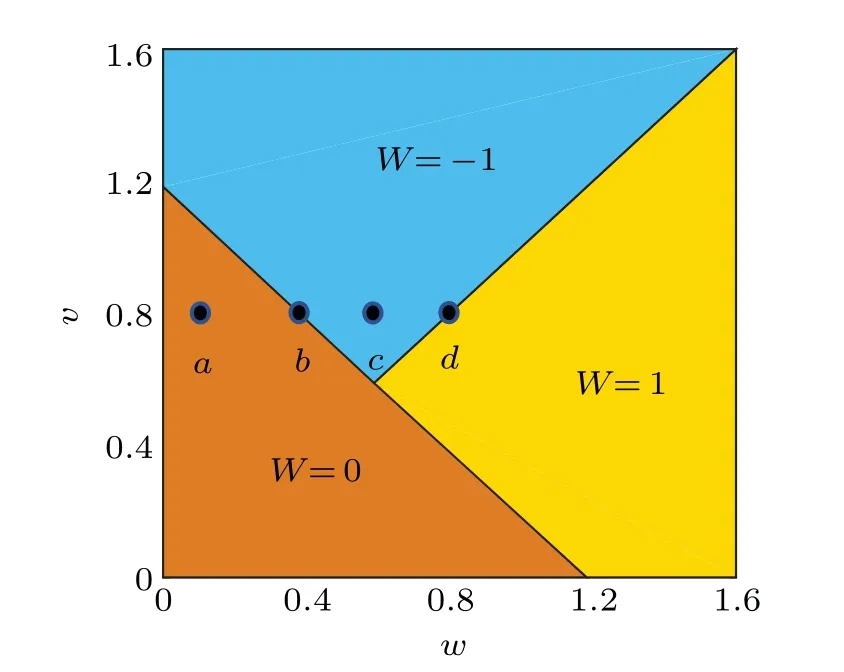
Fig.5. Phase diagram on the v-w plane with t1t2=1.4. The points a-d correspond to band structures in Figs.4(a)-4(d).

It is straight forward to show that the Hamiltonian(4)exhibits the following sublattice symmetry:

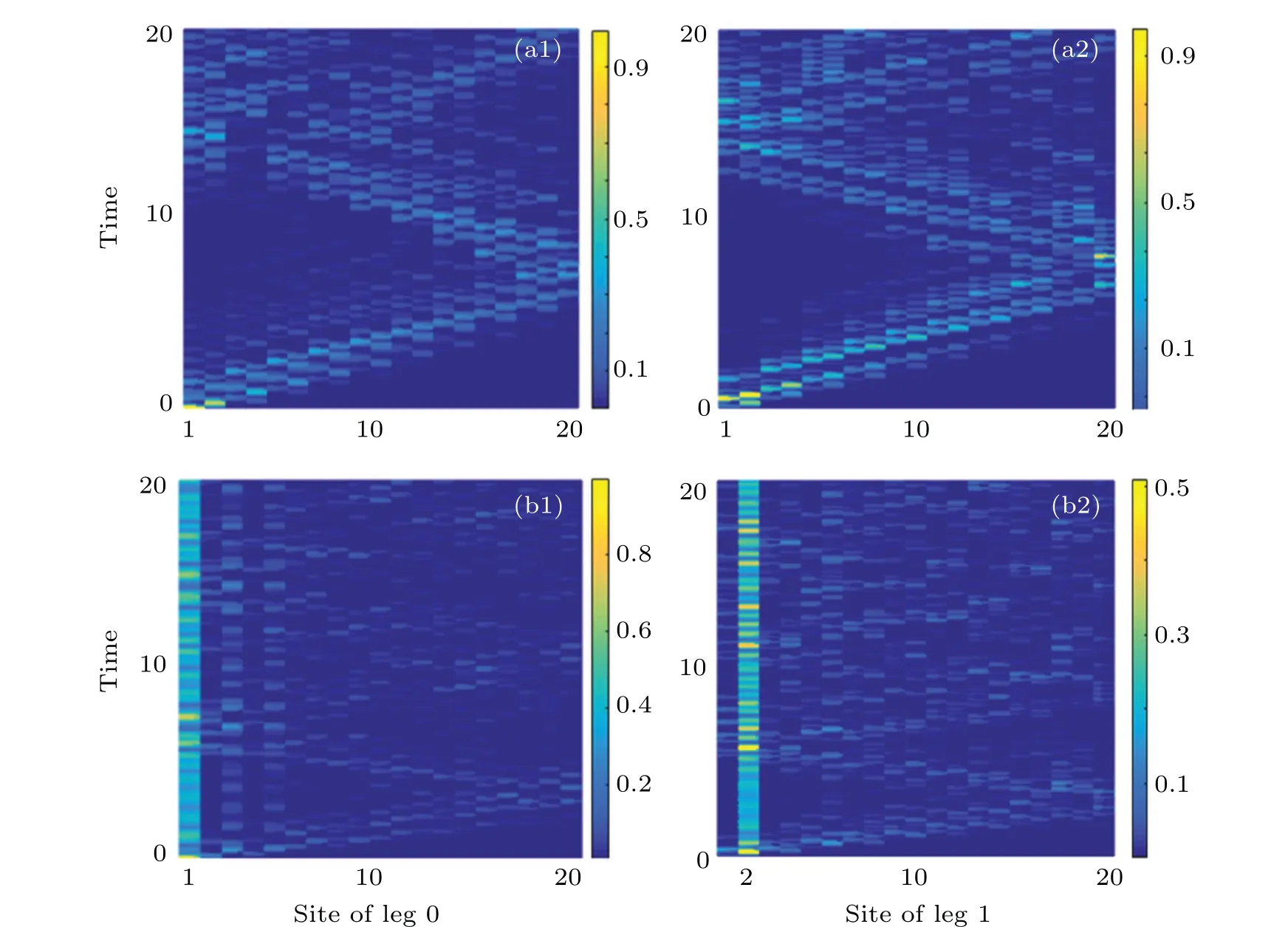
The semi-major axis of the ellipse isa=(w2+v2) and the center is(t1t2-2vw,0). While for(w+v)2t1t2,which produces non-zero winding number±1. The sign of the nonzero winding number is controlled by the direction of the curve governed by Eq.(10). That is, askincreases, Det|h(k)|goes clockwise(anticlockwise)around the origin forv>w(v

4. Edge state solutions

We now give an analytical expression of the edge states,which has been numerically depicted in Fig.3, to unambiguously demonstrate their type-II character. The eigenstates of Hamiltonian(2)assume the general form

which givesψ(b,1),j=-(t1/w)ψ(a,0),jandψ(a,1),j=-(v/t1)ψ(b,0),j.It can be seen from Eqs.(22)and(24)that,forv>w(v

5. Possible experimental observation

Fig.6. The time-averaged chiral displacement as a function of w. The red line is the theoretical prediction of the winding number. The blue line is the numerical simulation with N=10.The insets show the chiral displacement as a function of time. The other parameters are the same as those in Fig.3.

Fig.7. Population dynamics of the single-particle state initialized at the sublattice(a,0)of the first unit cell with v=0.6,t2=1.4 and N=10.(a1)[(a2)]plots the atomic distribution on leg 0(leg 1)with w=0.2. (b1)and(b2)are the same as(a1)and(a2)but with w=1.2.

The edge state can be detected by monitoring the atomic distribution on different momentum states. In experiment,we can suddenly turn off all laser beams, such that atoms evolve to different momentum states. Then we measure the absorption image and count the number of atoms in the different momentum states. For example, for a BEC initially prepared at the zero momentum state, the Raman couplings can be conveniently designed to produce a momentum lattice in which the initial state populates the sublattice (a,0) of the first unit cell. Therefore, the localization of the BEC on its initial state is a clear signature of the presence of edge state. As shown in Fig.7,we numerically calculate the dynamics of the atomic distribution for a BEC initialized at the zero momentum state for different coupling parameters. It is seen that,for(w+v)2>t1t2[Figs.7(b1)and 7(b2)],the BEC is localized at the sublattices(a,0)and(b,1)of the first unit cell,whereas it extends to the whole lattice sites for(w+v)2

6. Conclusion

In summary, we have proposed a feasible experimental scheme to study the topological properties of a two-legcoupled SSH model with staggered interleg hopping. It is found that this model supports two nontrivial topological phases and a trivial phase. By solving the eigenequations,we have predicted the presence of a type-II edge state.This can be regarded as an analog of type-II corner state in two dimension.Based on the relationship between edge state and topological invariant,we have built the bulk-boundary correspondence in our system. Moreover, possible experimental observation of the edge states and bulk topological invariants have been addressed.

Appendix A

The effective Hamiltonian can be readily read out from Eq.(A8)as

and

Acknowledgements

Project partially supported by the National Natural Science Foundation of China (Grant Nos. 12034012, 12074232,and 11804204)and 1331KSC.