High-efficiency asymmetric diffraction based on PT-antisymmetry in quantum dot molecules

Guangling Cheng(程廣玲) Yongsheng Hu(胡永升) Wenxue Zhong(鐘文學) and Aixi Chen(陳愛喜)

1Department of Applied Physics,East China Jiaotong University,Nanchang 330013,China

2Department of Physics,Zhejiang Sci-Tech University,Hangzhou 310018,China

Keywords: asymmetric diffraction grating,PT antisymmetry,tunneling effect

1. Introduction

As an optical element with periodic structure,the grating can diffract the incident light beam to a high-order diffraction direction,which has important applications in the field of industrial production and has also been widely concerned by researchers in the quantum field.[1]By replacing the travelingwave field with the standing-wave field in an electromagnetically induced transparency (EIT) system,[2,3]in which the absorption and dispersion become spatially periodic, electromagnetically induced grating (EIG) has been presented[4-6]and could provide the potential applications in quantum optics and laser physics.[7-9]For the probe resonance in the EIT medium, the dispersion is negligibly small with the transparency window and the medium acts as an amplitude grating,which leads to low-efficiency diffraction in the high-order direction. While the probe detuning appears,the dispersion will be enlarged with the small absorption and the grating could be formed. To improve the high-order diffraction intensities,the schemes for phase grating have been presented in different systems.[10-15]

Recently,the optical systems provide a versatile platform for the study of non-Hermitian physics with respect to paritytime (PT) symmetry and PT antisymmetry.[16-23]In particular, coherently prepared multilevel atoms may open up new opportunities for manipulating light in non-Hermitian optics,due to their easy reconfiguration, flexible tunability, actively control techniques,and enhanced nonlinear effects. Based on spatially modulating the refractive index with gain and absorption,the optical PT symmetry withn(x)=n*(-x)in the given direction has been theoretically and experimentally investigated in laser-driven multi-level atomic gases.[24-26]It is found that PT symmetry could be used to generate asymmetric diffraction grating.[27-30]As the counterpart of conventional PT symmetry, PT antisymmetry satisfyingn(x)=-n*(-x)has been investigated in the driven atomic systems,[26,31-34]which does not require optical gain and relaxes the condition of the interplay of gain and loss. PT antisymmetry has motivated various practical applications including unidirectional reflectionless,[31]constant refraction,[35]Hermitian scattering,[36]and coherent switch.[37]Most recently, PT antisymmetry is applied to explore asymmetric diffraction gratings in the Rydberg system[38]and atomic lattices.[39]

In parallel, semiconductor quantum dots have attracted a great deal of attention due to their distinct features[40-42]and are widely used in quantum optics to realize many interesting phenomena such as electromagnetically induced transparency,[43]four-wave mixing,[44]transfer of optical vortices,[45]and resonance fluorescence.[46]Importantly, the system of quantum dot molecules (QDM) formed via tunneling effect in two or more quantum dots has been brought into focus in recent years,[47-51]in which electrons can tunnel through the potential barrier between quantum dots. The tunneling effects between quantum dots play an important role in inducing coherent quantum phenomena such as slow light,[52]Kondo-peak splitting,[53]tunneling induced absorption,[54]tunneling-induced transparency,[55]and manipulation and exchange of light.[56]

Here, we investigate the properties of asymmetric light diffraction via the optical PT antisymmetry in the QDM system with the four-level structure, where the tunneling occurs between two quantum dots. Based on the spatial modulations of the driving field and driving detuning, the symmetric absorption and antisymmetric dispersion in the space are existent,which lead to the presence of PT antisymmetry. The results show that the asymmetric grating with high intensities in both the first-order and high-order directions are obtained via properly choosing the system parameters. Furthermore, the diffraction direction among the negative or positive orders can be controlled by changing the sign of the modulating detuning. Our scheme may be served as powerful building blocks for developing novel photonic devices and implementing the information processing.

2. Model and equation

We consider a system of asymmetric double quantum dots, where two individual quantum dots are coupled by tunneling.Such a system can be treated as a four-level system and it is shown in Fig. 1(a). A weak traveling-wave probe fieldEpwith frequencyωpprobes the transition of ground state|1〉to excited state|2〉, and a standing-wave driving fieldEcwith frequencyωcacts on excited state|3〉and excited state|4〉. The tunneling of two quantum dots exists between the transition|2〉 ?|3〉. The Rabi frequency of the probe and driving fields are Ωp=μ12·Ep/ˉhandΩc=Ω0sin(πx/Λ)withΩ0=μ34·Ec/ˉh,respectively,whereμi jis the associated dipole transition matrix element from state|i〉to|j〉andΛis the spatial period of the standing-wave driving field. Then,the Hamiltonian in the rotating frame and under the rotating-wave approximations is given by(ˉh=1)

withγibeing the total quantum dissipation of the energy-level|i〉including decay rate and dephasing rate. Under the condition of a weak probe fieldΩp?Ωc,Teand the initial condition ofρ11(0)=1 andρ22(0)=ρ32(0)=ρ42(0)=0,we solve the above equations and obtain the steady-state solution

whereΥ2=Δp-iγ2,Υ3=Δp+ω32-iγ3andΥ4=Δc+Δp+ω32-iγ4.We know that the polarization of the present system is determined byPp=Nμ12ρ21=ε0χpEp, whereN=Γ/Vis the electronic number density,Vis the volume of a single quantum dot.Then we can obtain the susceptibility of the fourlevel system to the probe field

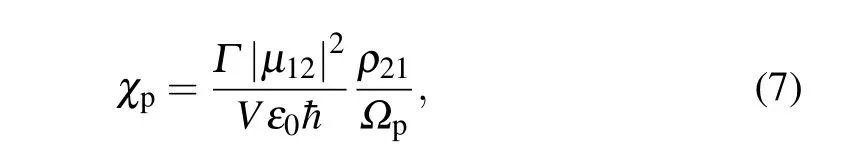
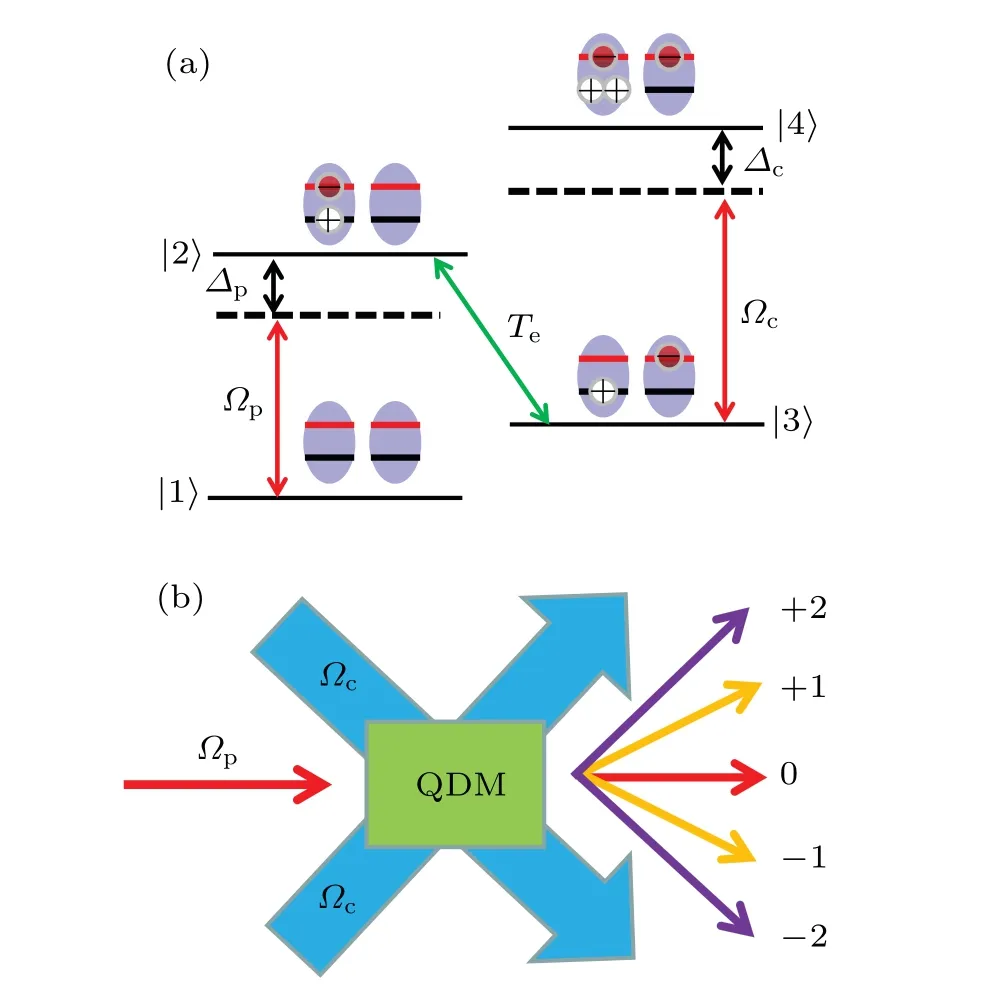
Fig. 1. (a) Diagram of the four-level QDM system with a probe field and a driving field. The electron and hole are shown by ?and ⊕, respectively. (b)Schematic propagations of driving field and probe field.

In the slow amplitude approximation and the steady-state regime, the dynamic response of the probe field can be described by Maxwell’s equation

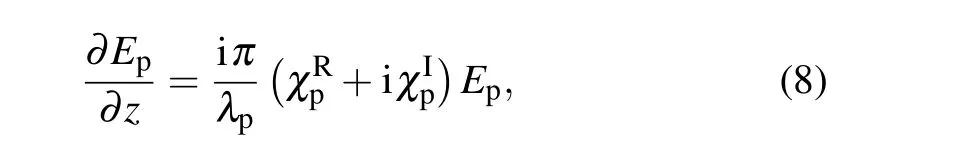
withλpbeing the wavelength of the probe field.Therefore,the transmission function of the probe field with interaction lengthLis derived as

wherez0=Vε0ˉhλp/(πΓ|μ12|2)is treated as an unit forL.The first term e-χIpL/z0and the second part eiχRpL/z0represent the amplitude and phase component,respectively. By solving the Fourier transform ofT(x),we can obtain the diffraction intensity of probe field,which is given by

whereΔc0is the constant detuning andδΔcdescribes the modulation amplitude of detuning. As shown previously,[28]the extra spatially modulated lasers are applied to induce the AC Stark effect, which could realize a periodic change of energy shift of state|4〉. It is expected that the combination of periodic modulation ofΩcandΔccan realize PT antisymmetry in the quantum dot system, where the symmetric absorption and antisymmetric dispersion,i.e.,χp(x)=-χ*p(-x),and the complex refractive index withn(x)=-n*(-x) via the relationn ≈1+χp/2 are reached and the interesting results will be achieved.

3. Result and discussion

Fig.2.Absorption χIp and dispersion χRp,transmission|T(x)|and diffraction patterns Ip(θ).The corresponding parameters are given by Δp=0,Te=2,Ω0=4,γ2=γ4=1=103γ3,L=20z0,M=10,Λ/λp=4,(a1)-(a3)Δc0=20,δΔc=0 and(b1)-(b3)Δc0=0,δΔc=20.

In the following,all physical parameters are measured in terms of decay ratesγ2and the actual experimental parameters of InAs self-assembled QDMs are selected withγ2=γ4=103γ3= 10 μeV.[58]We first discuss the influence of driving detuningΔcon the distribution of the system susceptibilityχp, transmission|T(x)| and diffraction intensityIp(θ)in Fig. 2, where the corresponding parameters are given byΔp= 0,Te= 2,Ω0= 4,γ2=γ4= 1 = 103γ3,L= 20z0,M=10,Λ/λp=4,(a1)-(a3)Δc0=20,δΔc=0 and (b1)-(b3)Δc0=0,δΔc=20. When the detuning of the driving field consists only of constant detuningΔc0=20,δΔc=0,as shown in Figs. 2(a1)-2(a3), we can see that absorption (reddashed) and dispersion (blue-solid) are even functions of coordinatex. As is expected, the probe field is diffracted symmetrically in both positive and negative directions and high efficiency at first-order diffraction. Differently,it is clear from Figs.2(b1)-2(b3)that the absorption is a symmetric function,but the dispersion becomes an antisymmetric function whenΔc0=0,δΔc=20. The PT antisymmetric region is formed due to the mutual modulations between driving detuning and standing-wave driving fields. In this region,transmission and diffraction shown in Fig. 2(b) greatly change compared with Fig. 2(a) and lead to the formation of asymmetric diffraction which only contains positive angles. It is obvious that QDM can successfully diffract a probe beam only in the positive direction under the action of PT antisymmetry. Compared with Figs. 2(a3) and 2(b3), we can see that the first-order diffraction of the classical symmetric grating can reach 0.168. However, under the condition of the same parameters, the asymmetric grating can reach 0.26,and the second-order diffraction can reach 0.164. Therefore, the grating with an asymmetric diffraction pattern could be achieved by introducing the modulation of driving detuning and meanwhile the diffraction efficiency is greatly improved.

Next, we focus on the influence of tunneling strengthTeand Rabi frequencyΩ0on diffraction intensity. The Fraunhofer diffraction patterns versus sinθfor the different parameters are illustrated in Fig.3 withL=25z0,Δc0=0,δΔc=25,and the other parameters as same as those in Fig. 2. As can be seen from Fig. 3(a), for the small tunneling intensity withTe=1, the diffraction of the probe field appears in the thirdorder direction, and its diffraction intensity can reach 0.134.Increasing tunneling strength toTe= 1.3 andTe= 2, the diffraction intensities in second-order and first-order diffraction peaks are 0.24 and 0.45, respectively. For the large tunneling strength ofTe= 3.3, the diffraction gradually tends to the center, and the intensity of higher-order diffraction is very small. The reason for this phenomenon is that the dispersion of the medium to the probe field decreases with the increase of tunneling intensity, which makes the diffraction tends to the zero-order direction. In contrast, when the Rabi frequency is small, the energy is concentrated in the central diffraction atΩ0=1.3 [see Fig. 3(b)]. As theΩ0continues to increase to 2, 3.5, and 4.6, the diffraction intensity gradually approaches the higher-order direction with values of 0.45,0.24, and 0.139, corresponding to first-order, second-order,and third-order diffraction,respectively.

Now we check into the effects of the modulation amplitudeδΔcof driving detuning and Rabi frequencyΩ0on the diffraction intensity of the asymmetric diffraction grating.The intensity of the diffraction peakIp(θn) (n=1,2,3) in Fig. 4 is based on the positive direction diffraction. We first analyze the first-order diffraction in Fig. 4(a). It is obvious that the first-order diffraction intensity has a high value near theΩ0=3,and increases with the modulation amplitudeδΔc. AtΩ0=3.1,δΔc=30, the diffraction intensity can reach the maximum value 0.462, and the second-order and third-order diffraction intensity is close to 0,which indicates that the energy of the probe field is well concentrated in the first-order direction.AsΩ0continues to increase,the first-order diffraction intensity gradually decreases to 0 and is not changing at the end. Second-order and third-order diffraction exhibit similar variations to the first-order diffraction,as shown in Figs.4(b)and 4(c). The difference is that the second-order diffraction is accompanied by a less intense diffraction region, and the third-order has two regions. This is because the diffraction peak is very sensitive to the value ofδΔcandΩ0,and with the increase ofΩ0,the dispersion of the medium to the probe field increases gradually, which causes the diffraction intensity to shift to the higher-order direction so that the diffraction peaks exhibit similar oscillatory behavior.In addition,by controllingδΔcandΩ0, we can obtain high-order diffraction with high efficiency, in which second-order diffraction can reach 0.249 and even the third-order diffraction can achieve a diffraction intensity as high as 0.145.

Fig. 4. The peak diffraction intensity Ip(θn) depending on the modulation amplitude δΔc and Rabi frequency Ω0, where the parameters are Te=2,L=25z0,Δc0=0 and the rest parameters are same as those in Fig.2.

As an asymmetric diffraction grating, it is vital to know how to control its diffraction direction. Thus, last but not least, we discuss the factors that influence the diffraction

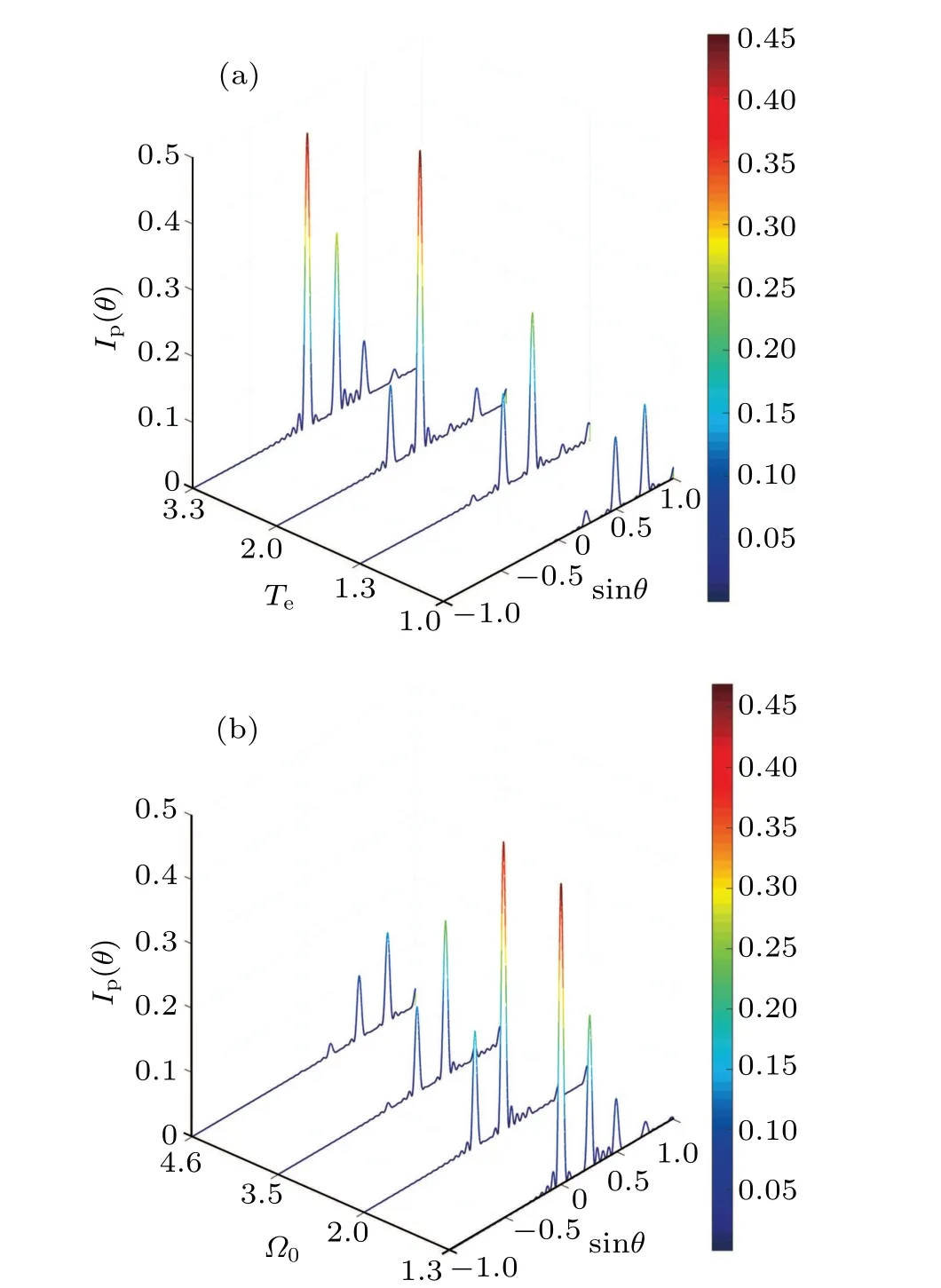
Fig. 3. The diffraction intensity Ip(θ) versus the coordinate sinθ at different Te and Ω0 with L=25z0, Δc0 =0, δΔc =25, (a) Ω0 =3,(b)Te=1.5,and the other parameters as same as those in Fig.2.

Fig.5. The diffraction intensity Ip(θ)as a function of sinθ and L with Δc0=0,[(a1),(a2)]δΔc=25,[(b1),(b2)]δΔc=-25,where the other parameters are the same as those in Fig.2.

direction of the asymmetric diffraction grating. Figures 5(a1)and 5(b1)show that the diffraction intensity changes with the interaction lengthLand sinθ. It is shown in Fig. 5(a1) that a diffraction pattern only has positive angle diffraction,which is realized by the modulation of absorption and dispersion relations in Fig. 5(a2) (δΔc=25). On the contrary, Fig. 5(b1)shows the diffraction pattern with negative angles, which is formed by the absorption and dispersion coefficients modulated in Fig. 5(b2) (δΔc=-25). For the present QDM system without gain, the positive and negative amplitude modulation of the detuning cannot change the symmetry of absorption modulation. Fortunately,by comparing to Figs.5(a2)and 5(b2),we can see that the change of the modulation amplitude of the driving detuning causes the switch of the positive and negative relation of the dispersion, which changes the direction of the diffraction from the positive angle to the negative angle. It is obvious that the diffraction direction of an asymmetric grating based on PT antisymmetry is mainly dependent on the spatial relation of the dispersion symbol,and it can be easily manipulated by simply changing the symbol of the modulation amplitude of the driving detuning. On the other hand,it can be seen from Figs.5(a1)and 5(b1)that,with the increase of the interaction lengthL,the diffraction intensity moves towards the higher-order direction due to the increasing phase modulation.

4. Conclusion

In conclusion, the asymmetric diffraction grating with higher diffraction efficiency is studied in the system of double quantum dots. Combining the tunneling effect between two quantum dots and the spatial modulations of the driving field and driving detuning,the system exhibits the complex refractive index withn(x)=-n*(-x). Then,the optical PT antisymmetry appears in such a system,which is responsible for the preparation of lopsided diffraction grating. It is obvious that the diffraction intensity in high-order direction exceeds that of the traditional symmetric grating and can be easily adjusted by changing the driving strength, detuning, tunneling strength,and interaction length.Our research provides a feasible scheme for greatly improving diffraction efficiency and effectively controlling diffraction direction,which is conducive to various applications of quantum information processing and optical transmissions.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11905064, 11775190 and 11565013) and the Scientific Research Foundation of Jiangxi Provincial Education Department, China (Grant No.GJJ200624).