鉻鉬系冷鐓鋼布氏硬度與抗拉強度相關關系的研究

徐海生，韓迎春，張 勇

（蕪湖新興鑄管有限責任公司，安徽 蕪湖 241002）

目前，在國內和國際市場上，冷墩用鋼具有廣闊的前景，而鉻鉬系冷墩鋼更是在汽車、船舶、設備制造、電子、家電等行業應用廣泛。根據不同的用途進行加工時，需要冷墩鋼材料本身既有良好的塑性（用硬度值來衡量）又能有一定的強度。因此，檢驗冷墩鋼的硬度和強度尤其重要。

而實踐證明，金屬材料的硬度值與強度值之間具有近似的相應關系[1]。因為硬度值是由起始塑性變形抗力和繼續塑性變形抗力決定的，材料的強度越高，塑性變形抗力越高，硬度值也就越高。因此，在一定的情況下可以通過測量硬度換算抗拉強度[2]。因此在冷墩鋼的質量判定中，可以通過硬度檢驗來反應冷墩鋼塑性的同時估算其強度。這樣既可以用來驗證檢驗的準確性，又可以用來在實驗室設備硬件不足的情況下只檢驗一個值來確定兩個指標，提高工作效率，節約成本。

但是由于受化學成分和制造工藝不同的影響，鋼鐵材料抗拉強度和硬度之間的換算關系存在著較大的分散性，而且熱軋冷鐓用盤圓，在矯直過程中也會對性能產生影響，因此現有的硬度和強度對應關系對冷墩鋼來說指導意義不強，所以根據實際生產探究一個比較準確的硬度和強度的換算關系就顯得尤為重要。

1 硬度和強度的回歸關系

1.1 試驗數據收集

隨機選取27組鉻鉬系盤圓冷墩鋼原材料，對其分別進行布氏硬度和抗拉強度的檢測，試驗數據如表1所示。

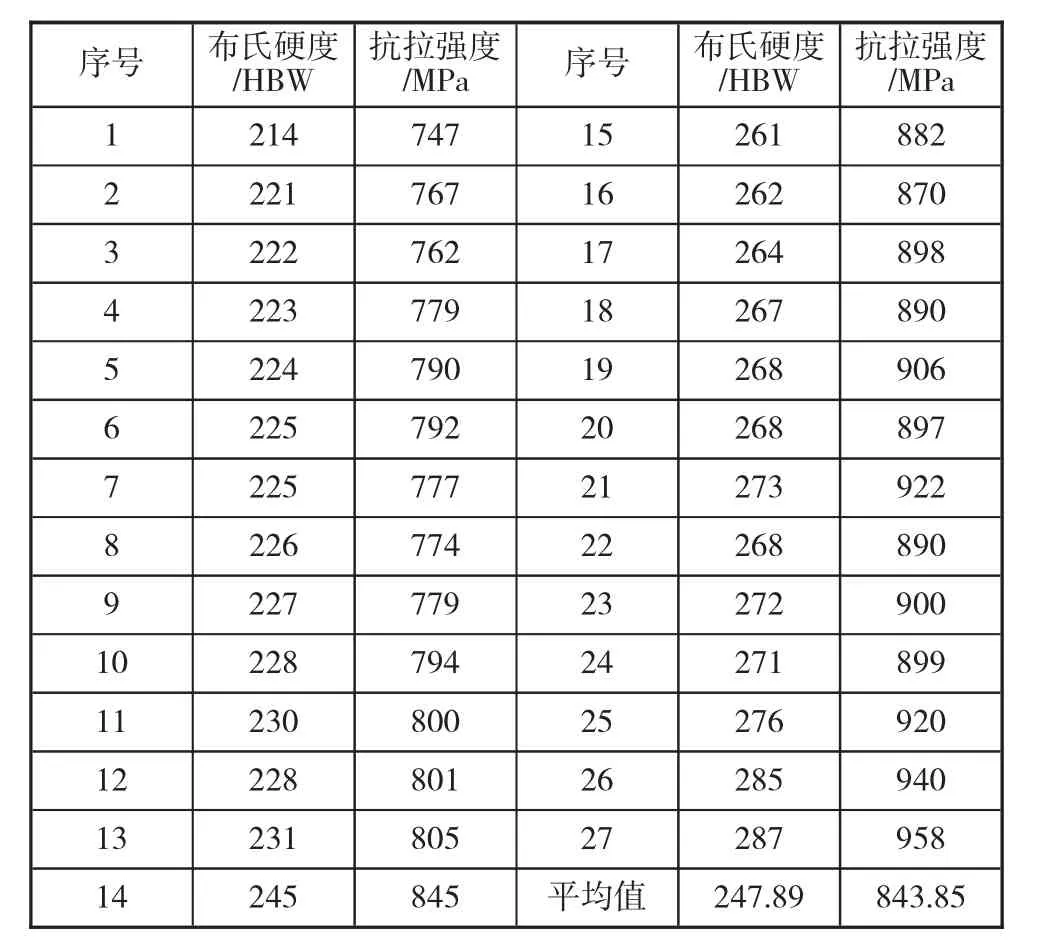
表1 鉻鉬系盤圓冷墩鋼的布氏硬度和抗拉強度數據表

1.2 數據結果分析

1.2.1 異常數據的檢驗與判定

采用萊特準則檢驗法判斷數據[3]：即第i個測量值xi所對應的殘差的絕對值大于3倍的標準偏差，則說明數據異常，應剔除不用。

通過計算，得出其殘差和標準偏差結果如下頁表2所示。

由表2可見：布氏硬度和抗拉強度數據的殘差絕對值均小于3倍的標準差絕對值，所以全部數值有效。

表2 布氏硬度和抗拉強度殘差和標準偏差數據表

1.2.2 布氏硬度和抗拉強度關系散布圖

根據實驗數據畫出布氏硬度和抗拉強度散布圖，橫坐標為布氏硬度，縱坐標為抗拉強度，如下頁圖1所示。由圖1可以看出，抗拉強度隨著布氏硬度的增加而上升。二者存在明顯的正相關關系。

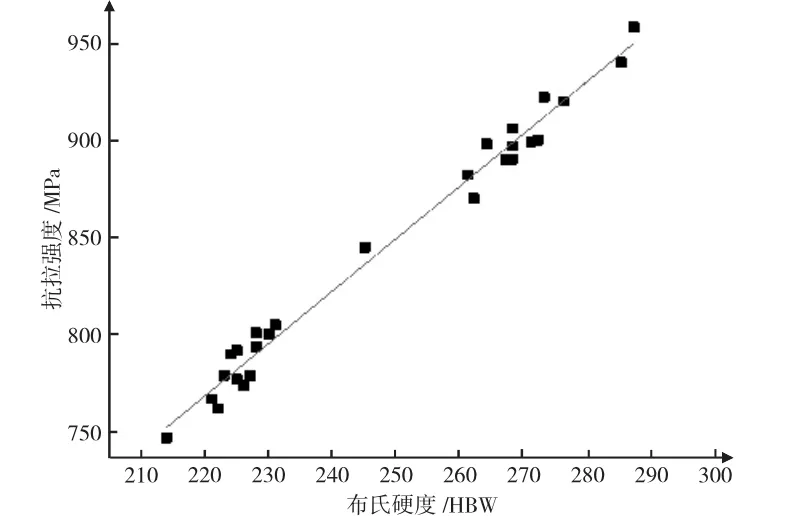
圖1 布氏硬度與抗拉強度散布圖

1.2.3 計算數據相關性

由圖1可知，雖然27個數據點基本在一條直線附近，但僅以散點圖無法確認變量布氏硬度是否是影響變量抗拉強度的主要因素。因此需要通過計算其相關系數r[4]來確認（y表示抗拉強度，x表示布氏硬度值）。

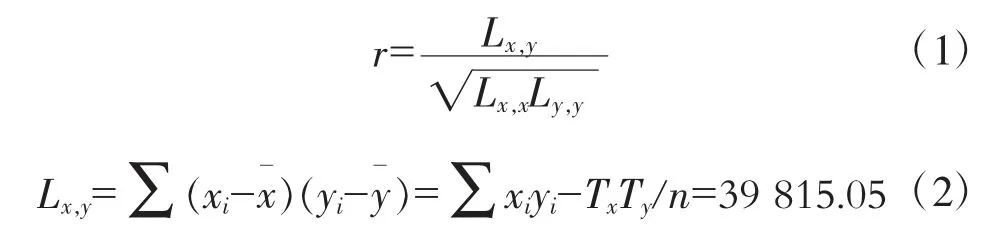
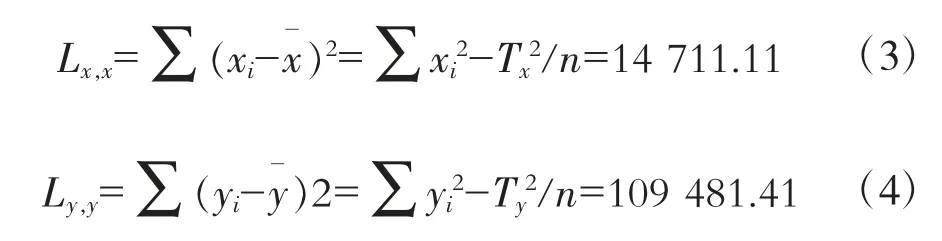
式中：Lx，y為布氏硬度x與抗拉強度y的方差；Lx，x為布氏硬度x的方差；Ly，y為抗拉強度y的方差。

因此：由（1）式可以求得相關系數r=0.99。

查相關系數r的臨界值表發現：當n=27時，自由度為n-2=25，在顯著性水平α=5%時的臨界值為0.381，而計算求得的r值為0.99，遠大于0.381，且已經接近于1，因此可以判斷鉻鉬系冷墩用鋼布氏硬度與抗拉強度之間存在正線性相關關系。

1.2.4 線性回歸方程擬合

在已經確定了鉻鉬系冷墩鋼布氏硬度與抗拉強度之間存在正線性相關關系的前提下可以假設抗拉強度（y）和布氏硬度（x）存在以下關系：

根據微分學，利用最小二乘法計算系數，定義函數：存在一個b和a的估計值b0，a0，使回歸估計值和y?和實際觀測值y的偏差平方和最小。即：

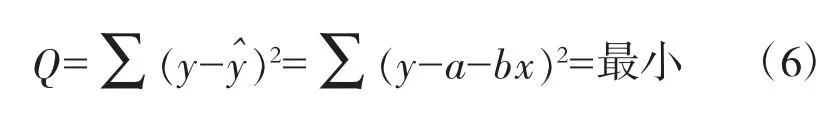
求極值，令Q對b和a的一階偏導數為0，得：

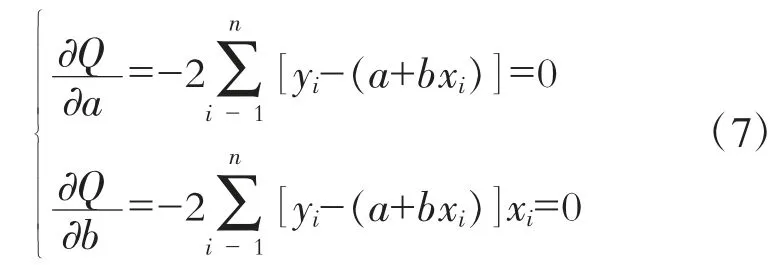
求解：

故求得鉻鉬系冷墩鋼布氏硬度與抗拉強度的線性回歸方程為：

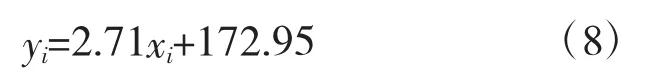
1.2.5 回歸模型的顯著性驗證

由于回歸方程是建立在實際檢驗數據的基礎上得出的，而在實際檢驗中，數據不可避免會有誤差，因此需要對回歸方程的顯著性進行驗證[5]。從而確定方程是否有意義。

根據統計學原理，顯著性驗證可以根據y的變異程度來檢驗。即：存在

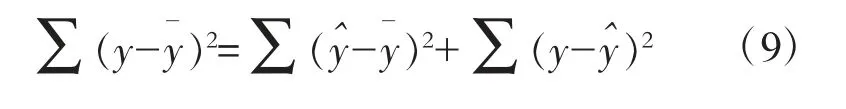
與此對應，y的自由度也存在：

利用F檢驗（方差法）驗證回歸方程的顯著性。

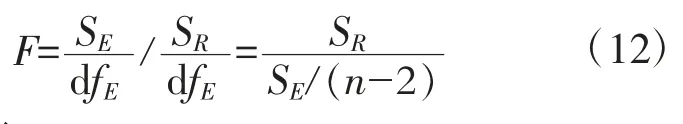
帶入數據計算：

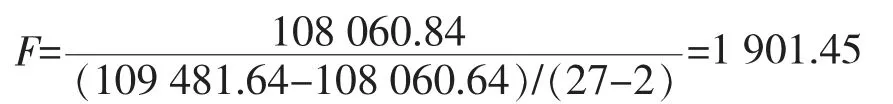
查F臨界值表，在α＝0.05時，F0.95（1，25）＝4.242；遠遠小于F=1 901.45；說明回歸方程在α＝0.05時，自變量布氏硬度和因變量抗拉強度之間存在極顯著的線性關系。

1.2.6 置信區間的計算

由于回歸方程是基于對試驗數據的平均預計，因此在實際檢驗中，通過回歸方程得到的抗拉強度估計值在多大程度上可以代替抗拉強度的真值，還需要構造一個區間，即進行參數檢驗的置信區間估計。

設yi的在概率1-α下置信區間為

抗拉強度服從正態分布有：

式中：σ為標準差；μ為平均值。

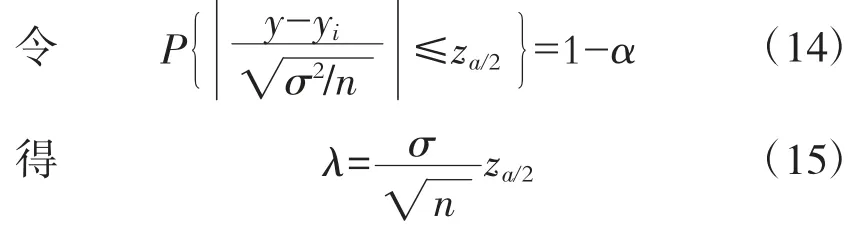
即y在置信度為1-α下的置信區間為：（）

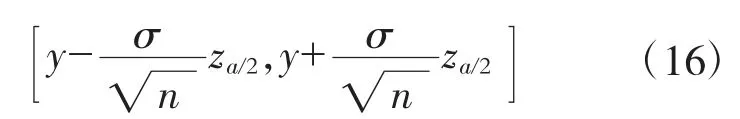
式中：α為抗拉強度y落在置信區間的置信度；P為抗拉強度y在置信度α下落在置信區間發生的概率。

取α=0.05，1-α=0.95；n=27，σ=63.68，查表得za/2=1.96，代入（15）式，計算得：

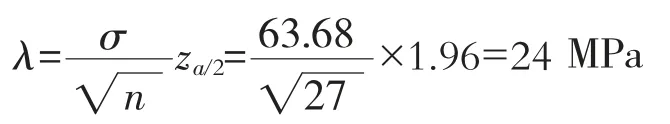
所以置信區間為[y-24，y+24]

即在95%的置信概率下，抗拉強度的真值落在回歸方程估計值±24 MPa的區間之內。

1.2.7 驗證回歸方程

再隨機選取10組鉻鉬系盤圓冷墩鋼原材料，對其分別進行布氏硬度和抗拉強度的檢測，并根據回歸方程對其抗拉強度進行估計。比較抗拉強度的估計值和實際值是否具有一致性。

由表3可以看出，10組試驗數據結果均落在置信區間內，其中除了6、9兩組試驗數據偏差大于λ/2，其余試驗數據均小于λ/2。說明抗拉強度的估計值和實際值具有很好的符合性。

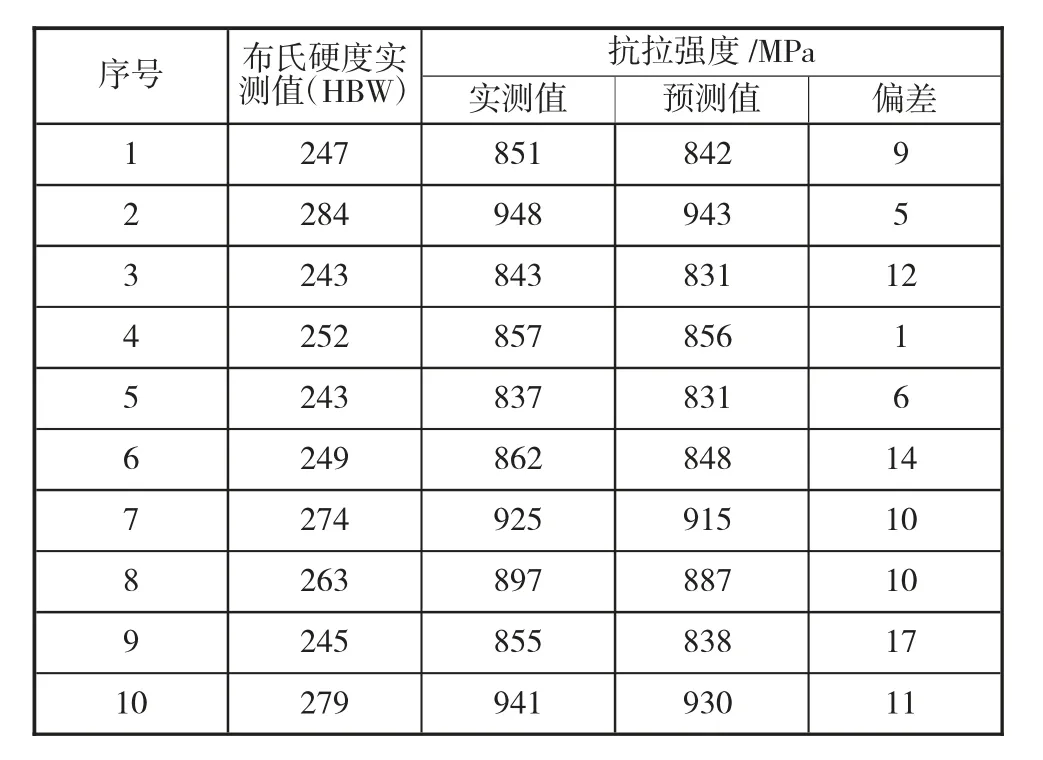
表3 抗拉強度的估計值和實際值偏差表

2 結論

1）鉻鉬系冷墩鋼布氏硬度與抗拉強度之間存在很強的線性關系，其線性回歸方程為yi=2.71xi+172.95。

2）線性回歸方程在α＝0.05時，其顯著性檢驗結果為F=1 901.45，遠遠大于臨界值，證明回歸方程具有實際意義。

3）對回歸方程進行置信區間驗證，說明鉻鉬系冷墩鋼的抗拉強度可以通過回歸方程進行預測，其結果具有很高的可信度。

4）本研究的結果可以使用在實際工程使用的鉻鉬系熱軋冷鐓用盤圓，用于指導生產，提高工作效率，節約成本。