強化學習在車輛路徑問題中的研究綜述

牛鵬飛，王曉峰，2，蘆 磊，張九龍

1.北方民族大學計算機科學與工程學院，銀川 750021

2.北方民族大學圖像圖形智能處理國家民委重點實驗室，銀川 750021

隨著經濟社會快速發展及交通基礎設施的不斷完善，城市物流業是當今社會關注的一個重要話題。2020年全國快遞業務量突破750億件，隨著構建新發展格局的加快，未來我國快遞業務量仍會保持較快的增長。物流業的快速發展使得對超大型物流系統的快速調度提出了更高的要求。車輛路徑問題（vehicle routing problem，VRP）是在車輛數一定的條件下，盡量縮短車輛行駛距離，找到一組總成本最小的路線。同時，根據優化目標不同，可以加入不同約束從而滿足不同種類問題的實際需求。

車輛路徑問題作為一個眾所周知的組合優化問題，最早由Dantzig和Ramser[1]于1959年作為卡車調度問題提出的，并被Lenstra 和Kan[2]證明是NP-難問題。經典的車輛路徑問題被定義為：有一個倉庫（depot）節點和若干個客戶（customers）節點，已知各個節點在二維空間上的位置和客戶的需求，在滿足約束條件下，使得車輛從倉庫節點出發訪問客戶節點，滿足客戶需求，最后返回倉庫。在不考慮負載的情況下，VRP等價于旅行商問題，應用到現實生活中，研究較多的是有容量約束的車輛路徑問題（capacitated vehicle routing problem，CVRP）[3]。當客戶的需求不定時，產生了隨機車輛路徑問題（stochastic vehicle routing problem，SVRP）[4]；當客戶對需求提出時間要求時，產生了帶時間窗的車輛路徑問題（capacitated vehicle routing problem with time windows，CVRPW）[5]；針對客戶當日要求交付的需求，產生了當日交付的車輛路徑問題（same-day delivery problem with vehicle routing problems，SDDVRP）[6]。關于VRP的詳細描述見文獻[7]。

多年來大量國內外學者致力于VRP 的研究，目前求解VRP的主要方法分為常規算法和基于強化學習的算法，其中常規算法包括精確算法、啟發式算法等。基于強化學習的算法主要包括基于馬爾科夫決策過程的強化學習和近年來方興未艾的深度強化學習。

本文將首先簡略概述基于常規算法求解VRP的各類算法，再對基于強化學習求解VRP 的各類模型進行詳細的介紹。

1 基于常規方法求解VRP技術

目前求解VRP 的常規算法包括精確算法、啟發式算法和元啟發式算法。

（1）精確算法主要包括線性規劃法[8]、分支限界法[9]等。這類算法適用于VRP規模較小、結構簡單的情況，當VRP 中有較多約束條件時，精確算法無法在有效時間內得到問題的最優解。

（2）啟發式算法主要包括節約法[10]、線性節約法[11]和插入檢測法[12]等。這類算法適用于規模較大的VRP，面對CVRP、CVRPW 等這些有較多約束條件的VRP 變種問題時，該類算法仍較為快速求解，具有求解效率高、占用內存少的優勢，因為該類算法改進目標一直是求解速度，因而問題規模增大時無法得到最優解。

（3）元啟發式算法主要包括模擬退火算法[13]、禁忌搜索算法[14]、基于群思想的算法[15-18]等。這類算法具有求解速度快、效率高的特點。但這類算法在求解VRP時容易陷入局部最優而無法得到全局最優解，以及不容易收斂等問題。

表1 對上述求解VRP 的各類常規算法的缺點進行了對比。

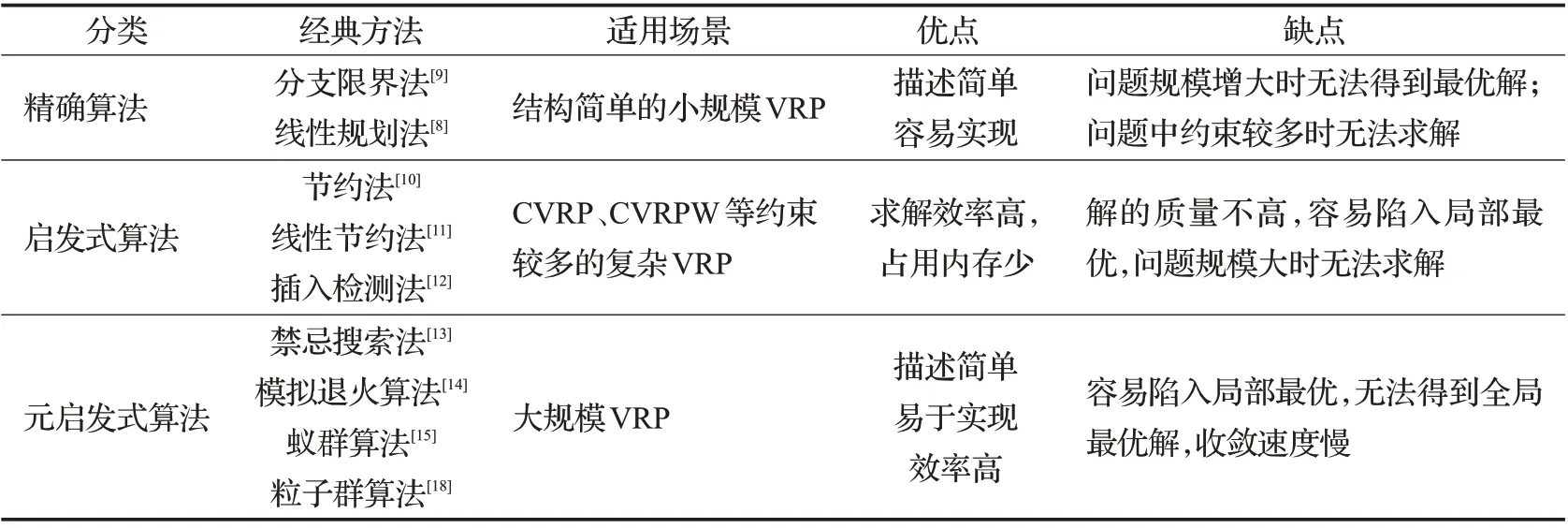
表1 求解車輛路徑問題的常規方法優缺點對比Table.1 Comparison of advantages and disadvantages of conventional approaches applied to VRP

2 強化學習概述

2.1 強化學習基礎

強化學習（reinforce learning，RL）是人工智能的一個重要分支，它不需要監督信號來進行學習，而是依賴個體（agent）在環境（environment）中的反饋回報信號，依據反饋回報信號對個體的狀態和行動進行更正，使得個體逐步實現獎勵（Reward）的最大化，從而使得強化學習具有較強的自主學習能力。強化學習的描述如圖1所示。

圖1 強化學習示意圖Fig.1 Schematic diagram of reinforce learning

2.2 強化學習算法分類

對強化學習算法的分類可以根據有無模型分為基于模型（model-based）和無模型（model-free）的學習算法。在求解VRP中常見的基于模型的學習方法有動態規劃法；無模型的學習算法主要有基于價值的時序差分算法[18]、Q-learning 算法[19]、DQN 算法[20]等；基于策略的REINFORC算法[21]，價值和策略相結合的Actor-Critic算法[22]、Advantage Actor-Critic 算法等。如圖2 總結了一些已經應用到VRP求解中的經典強化學習算法。

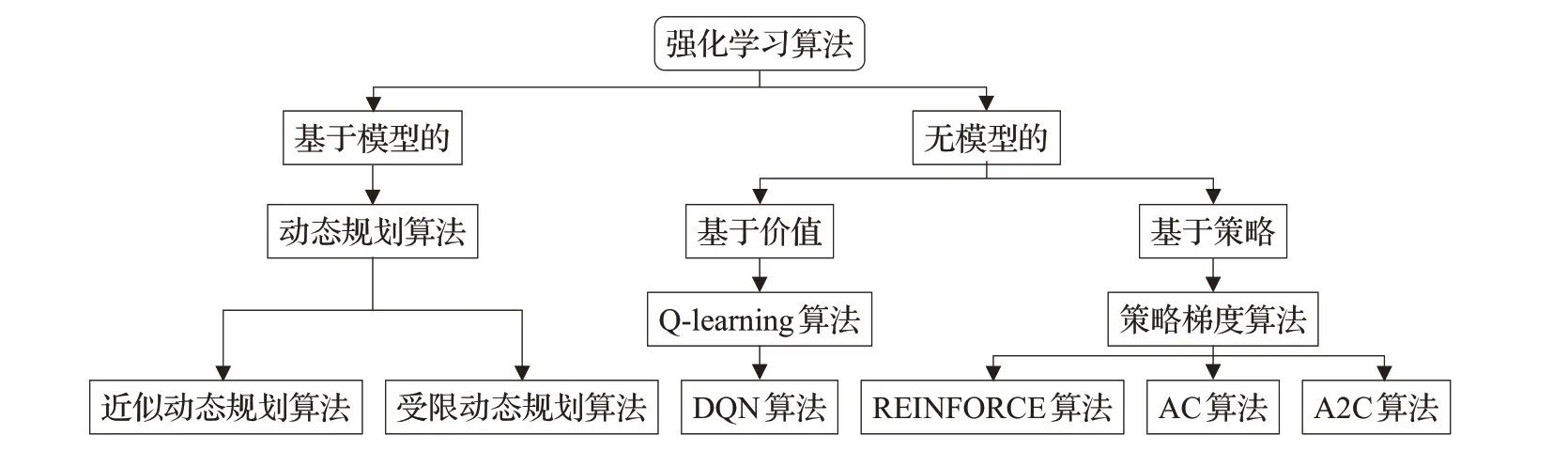
圖2 強化學習算法分類圖Fig.2 Classification diagram of reinforcement learning algorithm

3 基于模型的算法

在強化學習中“模型”指環境，基于模型的強化學習算法意為通過預先給定或通過學習的方式得到MDP模型。最典型的給定環境模型方法是打敗圍棋冠軍柯潔的阿爾法狗算法，通過學習的環境模型方法有world models 算法[23]。在VRP 求解中運用最多的基于模型的強化學習算法為動態規劃算法，及由動態規劃算法衍生出來的近似動態規劃算法和深度神經網絡動態規劃算法。基于模型的算法通過MDP模型預測以后可能的狀態S和動作A，從而對個體行動提供指導，但在現實生活中環境模型可能很復雜以至于難以建模。

3.1 動態規劃算法

動態規劃算法是由美國數學家Bellman在研究多階段決策過程的優化問題時提出的，“動態規劃”一詞中“動態”意為問題是可以通過一個個子問題去求解，“規劃”意為優化策略。在給定一個用馬爾科夫決策過程描述的完備環境模型下，其可以計算最優的模型。在強化學習中，動態規劃算法的目的是使用價值函數求解最優策略，常規的動態規劃算法因“維數災難”無法有效的求解強化學習問題，但后續其他的方法都是對動態規劃算法的改進和近似。運用動態規劃算法求解強化學習問題就是求解給定策略π時對應的價值V*(S) 。價值V*(S)表示為：

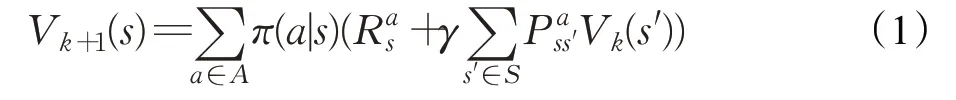
公式表示k+1 輪的價值Vk+1(s)可由前k輪的Vk(S)出來，策略π(a|s)為給定狀態s時選擇動作a的概率，Ras為給定狀態s時選擇動作a的獎勵，γ為折扣率，為下一步狀態的概率乘以價值函數之和。

3.1.1 基于近似動態規劃的方法

Secomandi 等人[24]將首次神經網絡近似動態規劃（network approximate dynamic programming，NDP）方法應用到求解帶有隨機需求的VRP 中，NDP 是在動態規劃中使用神經網絡對策略進行近似的新模型，實驗結果表明在有隨機需求的VRP中，基于rollot策略的NDP算法的性能要優于近似策略迭代的NDP 算法。Tatarakis和Minis[25]對隨機需求下有倉庫補貨的單車輛路徑問題（stochastic vehicle routing with depot returns problem，SVRDRP）進行了研究，通過對交付產品的劃分，提出了一種近似動態規劃算法從而在合理的時間內可得到最優策略。

針對運輸和物流中出現的隨機優化問題，Powell等人[26]在2012年提出了一個完整的研究框架，其中對近似動態規劃（ADP）算法在動態VRP的應用做了細致的說明。?imen和Soysal[27]將VRP的優化目標從成本最小化更改為排放最小化，從而給出了綠色帶時間窗有容量約束的隨機車輛路徑問題（green stochastic time-dependent capacitated vehicle routing problem，GSTDCVRP）的MDP模型和基于近似動態規劃的啟發式算法。

Ulmer等人[28]利用近似動態規劃的方法對價值函數進行近似，從而提出了有求解隨機服務請求的車輛路徑問題（vehicle routing problem with stochastic service requests，VRPSSR）的ATB算法。為降低VRP中因客戶的隨機需求帶來的高額計算，Ulmer 等人[29]針對隨機服務請求的單車輛路徑問題（single-vehicle routing problem with stochastic service requests，SVRPSSR），將客戶請求服務的時間以及客戶自身的空間位置納入近似動態規劃中，從而生成動態的路線策略。

為降低由交通擁堵引起的成本，Kok 等人[30]針對CVRPW，在近似動態規劃算法中加入了避免交通擁堵的策略，結果表明該方法能夠有效降低通勤中擁堵時長。Secomandi等人[31]針對只有一輛車的隨機需求車輛路徑問題（SDVRP），通過有限階段的MDP進行建模，使用部分再優化（partial reoptimization）的方法對SDVRP進行研究，并通過PH、SH兩種啟發式算法選擇MDP的狀態子集，以此來計算最優策略。Goodson 等人[32]提出了基于rollot 策略的近似動態規劃框架，并將該框架應用于求解具有隨機需求和持續時間限制的多車輛路徑問題（vehicle routing problem with stochastic demand and duration limits，VRPSDL）。

3.1.2 基于深度動態規劃的方法

Kool 等人[33]提出了結合學習神經啟發式和動態規劃的深度策略動態規劃對VRP 進行求解，模型根據圖神經網絡（graph neural network，GNN）得到的每個客戶頂點特征向量，通過注意力機制計算每個客戶頂點被選中的概率，并將這個概率作為動態規劃算法對部分解進行選擇的策略，最后根據此策略構造最優解。

3.1.3 基于動態規劃的方法總結

常規方法通常只能求解靜態確定性問題，難以求解帶有動態和隨機信息的問題。動態規劃算法可有效求解靜態車輛路徑問題和動態車輛路徑問題，具有求解范圍較廣的優勢。求解車輛路徑問題時，需首先建立MDP模型，設計算法求解該模型，并用rollout策略在啟發式算法基礎上得到最優值函數，但動態規劃算法無法解決客戶節點規模大的車輛路徑問題。因此，學者們設計出近似動態規劃算法，利用神經網絡的泛化能力，通過價值函數近似或策略函數近似得到獎勵函數，從而不用直接求解貝爾曼方程，解決了動態規劃算法帶來的“維數災難”問題。學者們的改進方向主要是近似動態規劃算法中神經網絡的結構，其主要區別是針對不同車輛路徑問題中的各類相關信息進行編碼作為神經網絡的輸入信息，輸入的信息越豐富，獎勵函數的近似精度就越高，進而近似動態規劃算法的優化效果越好。其次是對rollout策略的改進，以減少模型的計算成本和計算量。

相較于傳統運籌學有建模不準確的問題，以近似動態規劃算法為代表的基于模型的強化學習算法，可以通過智能體與環境不斷交互學習到最優策略。在動態車輛路徑問題中動態規劃算法可以在于環境交互的過程中不斷加入獲取的隨機信息。基于以上優點使有模型強化學習算法適合求解具有動態結構和隨機信息的車輛路徑問題。

3.1.4 動態規劃算法局限性分析

動態規劃算法在車輛路徑問題等領域中應用較廣。但也存在許多問題，比如維數災難、系統不可知、實時求解效率低、近似動態規劃算法雖能有效避免上述問題但也因采用神經網絡，其魯棒性較差。分析原因如下：

（1）維數災難

現實生活中的車輛路徑問題規模較大，以至于通過MDP 建模以后動作空間和狀態空間過大，導致動態規劃算法失效。因而動態規劃算法在求解大規模車輛路徑時性能較差。

（2）系統不可知

動態規劃算法可求解靜態的車輛路徑問題和動態的車輛路徑問題但需對問題先建模，但實際場景中的車輛路徑問題因系統的狀態轉移函數未知，從而無法對問題進行建模，或對問題進行過理想化處理，使得動態規劃算法應用受限。

（3）實時求解效率低

當下車輛路徑問題求解的實時性要求不斷提高，即需要在較短的時間內給出問題的解，動態規劃算法雖能給出問題的最優解，但耗費的時間較長且求解的效率較低。通過神經網絡計算的近似動態規劃算法雖能比動態規劃算法求解算法快，但因當前計算機的性能，算法實時求解能力仍有待提高。

（4）魯棒性差

目前改進的動態規劃算法均是采用神經網絡結構，且使用自舉采樣的方式獲取數據，數據的關聯性較高，算法的魯棒性較差，且算法的抗擾動能力較弱。使得近似動態算法在實際生活中的車輛路徑問題應用有限。

3.1.5 基于動態規劃求解VRP分析對比

表2 將上述基于動態規劃求解VRP 的各類模型的訓練方法、求解問題、以及優化效果進行了對比。

表2 基于動態規劃求解車輛路徑問題的方法對比Table 2 Comparison of approaches of dynamic programming applied to VRP

4 無模型的算法

無模型的強化學習算法是指MDP模型中的環境參數未知，即在給定狀態條件下個體采取動作以后，未來的狀態和獎勵值未知。因此，個體不對問題進行建模，而是先和環境進行交互，在不斷試錯中尋找最優策略。無模型的強化學習算法主要分為基于值函數進行優化的算法、基于策略進行優化的算法、值函數和策略結合進行優化的算法。

4.1 基于值函數的算法

基于值函數的強化學習算法通過對值函數進行優化從而得到最優策略。在VRP 中，值函數是對路徑策略π優劣的評估，值函數分為狀態價值函數V*(s)和狀態-動作價值函數q*(s,a)，V*(s)表示為：

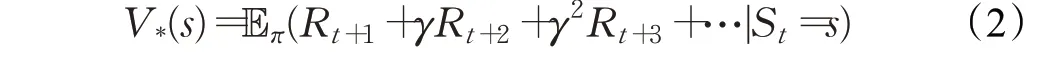
q*(s,a)表示為：

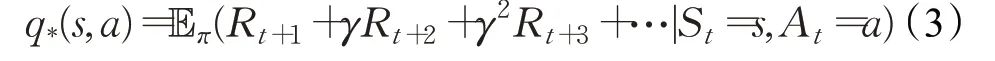
在求解VRP 中，基于值函數的強化學習算法主要有時序差分算法、Q-learning 算法、DQN 算法、Dueling DQN算法。

4.1.1 時序差分算法

時序差分算法由Wang 等人[14]提出，是強化學習的核心算法之一，它結合了動態規劃算法和蒙特卡洛方法的原理，是通過部分狀態序列來求解問題的強化學習算法。在時序差分算法中，價值函數的更新是通過兩個連續的狀態和其的獎勵值的差來實現的。最基本的時序差分算法的價值函數更新公式為：

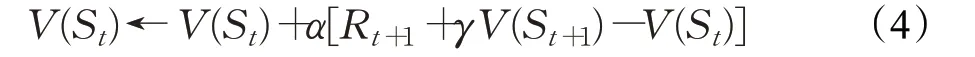
其中α為學習率，Rt+1+γV(St+1)-V(St)為時序差分誤差，因此使用這種更新方法的時序差分也被稱為單步時序差分。

針對帶時間窗的動態車輛路徑問題（CDVRPTW），Joe 和Lau[35]提出了DRLSA 模型，通過基于神經網絡的時序差分算法和經驗放回策略去近似價值函數，然后運用模擬退火算法生成路徑。實驗表明，DRLSA 模型在有48 個客戶節點的CDVRPTW 上優化效果超越了經典的基于值函數近似算法和MSA 算法。該方法解決了當動態請求普遍存在時，該如何給出有效的路徑規劃。

時序差分算法作為經典的無模型算法，對模型環境要求低，無需訓練結束即可獲得各類參數的增量。在規模較小的車輛路徑問題中優化效果較好，但收斂速度較慢，作為表格型傳統強化學習算法不足以解決復雜的車輛路徑問題。

4.1.2 Q-learning算法

Q-learning算法是Watkins等人[19]提出的，該算法求解強化學習問題時，使用兩個控制策略，一個策略用于更新動作，另一個用于更新價值函數，核心思想為離軌策略下的時序差分控制。Q-learning算法在強化學習的控制問題中應用最為廣泛。該算法價值函數的更新公式為：

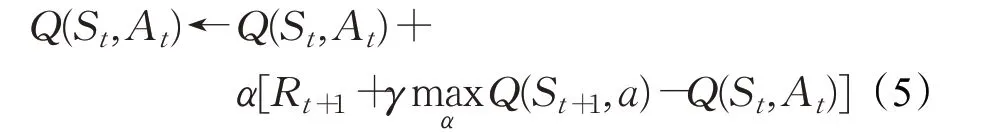
其中α為學習率，Rt+1為t+1 步的獎勵，α為狀態St+1能執行的動作。

Zhang等人[34]提出來一種基于查找表的值函數近似VFA模型求解帶有隨機需求的VRP。具體來說，將當前狀態和決策的重要信息存儲在一個Q-表中，并用改進的Q-learning算法進行學習。

針對多任務的車輛路徑問題，Bouhamed 等人[36]提出了一種基于Q-learning 算法的多任務代理路由調度框架。該模型首先將與任務相關的時間段定義為一個集合，并據此設計出了相應的Q-表，再通過Q-learning算法對Q-表進行更新從而對問題進行求解，實驗結果表明，該模型在復雜的VRP 上優化效果接近目前最優方法。

Q-learning 算法因優先執行動作，主動探索能力強。可有效的求解帶有隨機需求信息的車輛路徑問題。但因是把狀態和不同的動作存儲在Q 表中并一直更新，易使算法陷入局部最優，降低算法的學習效率，搜索耗時較長。更新Q表時Q表一直發生動態變化，所以更新的效果不穩定。

4.1.3 DQN算法

DQN算法是Mnih等人[20]提出的，該模型將Q-learning算法與深度神經網絡相結合起來，通常使用DNN 或者CNN來構建模型，使用Q-learning算法訓練。DQN算法對Q-learning 的改進主要有以下兩個方面：（1）DQN 算法利用神經網絡逼近值函數。（2）DQN算法利用了經驗回放訓練強化學習的學習過程。DQN算法的損失函數如下：

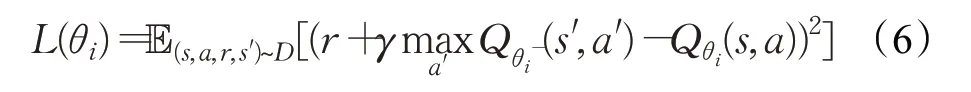
目前，DQN 算法在VRP 中的應用是一個新興的研究熱點，國內外的主要研究成果有：

針對帶有多個倉庫（depots）的車輛路徑問題（MDVRP）和動態車輛路徑問題，Bdeir 等人[37]提出了基于DQN 的RP-DQN 模型，該模型框架如圖3 所示。RP-DQN 模型中為有效降低問題的計算復雜性，編碼器不僅對靜態的客戶節點位置、客戶需求進行編碼，并對問題中的動態特征信息進行編碼，使用Q-learning 算法對模型進行優化。在客戶數量為20、50、100 的CVRP 上優化效果均超過了Kool 等人[38]的方法。首次將深度Q 網絡運用到MDVRP 的求解過程中，在客戶數量為20、50、100 的MDVRP上RP-DQN模型的優化效果也好于Kool等人[38]的方法。總體來說RP-DQN 模型的泛化能力要高于Kool等人[38]提出的AM模型。

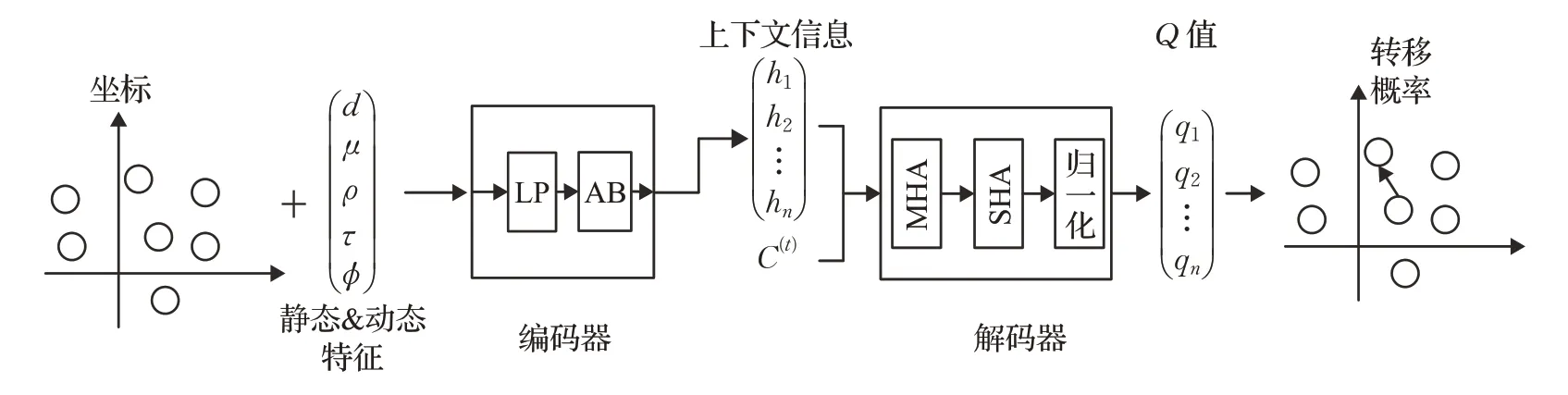
圖3 RP-DQN模型示例Fig.3 Example of RP-DQN model

針對客戶當日要求交付（same-day delivery）的需求，Chen 等人[39]提出了車輛和無人機的當天交付問題（same-day delivery problem with vehicles and drones，SDDPVD），建模過程中采用和Powell[26]相同的模型架構，并使用Ulmer等[40]提出的路由策略來模擬路線的更新和演變，首先將SDDPVD 建模為MDP 模型，為了使決策快速有效，將動作空間和狀態空間進行簡化，通過設計DQN算法去近似每個特征向量的值。

4.1.4 DQN算法總結

DQN算法作為具有里程碑意義的深度強化學習算法，不同于傳統強化學習算法中值函數線性近似方法，使用多層深度神經網絡近似代替Q-learning 算法中的Q-表，從而可以將高維輸入值映射到Q-空間。DQN 算法通過一個經驗池來存儲以前的數據，每次更新參數的時候從經驗池中抽取一部分的數據來更新，打破信息間存在的關聯，從而可有效求解有狀態、動作高維復雜，數據間彼此有關聯的車輛路徑問題。

基于DQN算法求解車輛路徑問題的各類模型主要是通過對DQN算法的狀態、動作、獎勵的表示做出相應的修改，對價值函數進行映射，通過對價值函數做出評價，以此改進初始策略。但DQN 算法在求解車輛路徑問題仍存在很多不足，比如因需對Q-網絡進行最大化操作引起過估計問題，DQN 算法只能求解單車輛的車輛路徑問題。

4.1.5 DQN算法局限性分析

DQN 算法因運用經驗放回機制和設定一個固定Q目標值神經網絡，具有較好的收斂性和兼容性。但在車輛路徑問題求解中也存在較多問題，例如過擬合問題、樣本利用率低、得分不穩定。具體以上問題原因為：

（1）過擬合問題

DQN 算法在訓練智能體過程中，會采用Q 網絡最大化的操作，從而出現過度適應當前環境的情況，使算法出現過擬合現象。

（2）樣本利用率低

DQN 算法和環境交互的過程中，樣本之間有很強的關聯性，降低了深度神經網絡的更新效率，算法需要很長的時間才能達到合適的得分標準，使得DQN 算法在車輛路徑問題中的數據樣本利用率較低。

（3）得分不穩定

使用DQN算法求解車輛路徑問題時，Q-learning學習過程中會對Q值過高估計，容易產生較高誤差，導致算法穩定性較差，得分性能不穩定。

4.1.6 Dueling DQN算法

針對無模型的強化學習問題，Wang 等人[41]提出了一種新的DQN 模型：Dueling DQN（DDQN）。不同于DQN 算法，DDQN 算法把在卷積層得到的特征分為狀態值和動作優勢函數兩部分：

式中，Qπ(s,a)為狀態s下選擇動作a的獎勵值，狀態值Vπ(s)是對狀態s的評價，動作優勢函數Aπ(s,a)是對狀態s下各個動作優劣的評價指標。

Zhang等人[42]為有效解決車輛路徑問題中的供需匹配難題，提出了QRewriter-DDQN 模型。將可用車輛提前調度給需求級別高的客戶。QRewriter-DDQN模型由Qrewriter 模塊和-DDQN 模塊構成，DDQN 模塊將車輛和客戶之間的KL分布作為激勵函數，從而得到供需之間的動態變化。之后，運用Qrewriter 模塊用來改進DDQN生成的調度策略。

4.1.7 Dueling DQN算法總結

Dueling DQN 算法是通過改進深度神經網絡的結構來提高DQN算法性能。該算法采用卷積神經網絡處理車輛路徑問題中的初始信息，并使用兩個全連接神經網絡把Q值劃分為狀態值和動作優勢函數兩部分，通過這種改變可以有效地區分出獎勵值的來源。因為優勢函數存在，Dueling DQN算法可以讓一個狀態下的所有動作同時更新，加快了算法收斂速度。尤其是在有大規模動作空間的車輛路徑問題中，相較于初始DQN 算法Dueling DQN算法能更加高效的學習價值函數。

4.2 基于策略的方法

以上基于值的算法是通過值函數近似方法對價值函數進行參數化比較，從而使個體選擇相應動作。另一種常見的是基于策略的算法，直接對策略進行優化，尋找最優策略。常用于VRP的基于策略的算法有蒙特卡洛REINFORCE算法、Actor-Critic算法等。

基于策略的算法具有策略參數化簡單、收斂速度快的優點，且適用于連續或者高維的動作空間。策略就是策略參數化，即πθ，參數化后的策略為一個概率密度函數θ。與策略相對應，策略搜索分為隨機策略搜索和確定性策略搜索。策略搜索的目的就是找到最優的參數θ，定義目標函數：

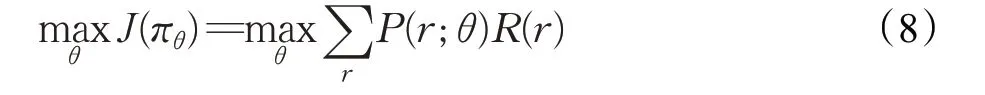
定義策略梯度公式為：

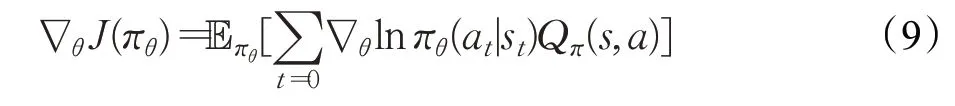
更新策略的參數：

4.2.1 蒙特卡洛REINFORCE方法

蒙特卡洛REINFORCE 方法是最簡單的策略梯度算法[43]，該算法使用價值函數V*(s)來近似代替策略梯度公式里面的Qπ(s,a)，首先輸入N個蒙特卡洛完整序列，用蒙特卡洛方法計算每個時間位置t的狀態價值Vt(s)，再按照以下公式對策略θ進行更新：

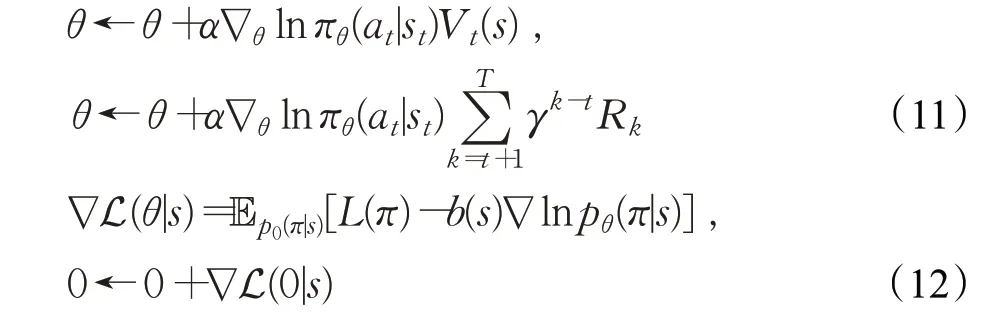
不斷執行動作直到結束，在一個回合結束之后計算總反饋，然后根據總反饋更新參數。pθ(π|s)為每一步動作選擇概率的累乘，則lnpθ(π|s)則為每一步動作選擇概率對數的求和，?lnpθ(π|s)為梯度值，L(π)-b(s)為梯度下降的方向，b(s)為策略的平均表現。

自Vinyals等人[44]在2015年提出了指針網絡（Ptr-Net）模型求解旅行商問題后，在小規模的旅行商問題上，相較于傳統的啟發式搜索算法。該模型具有求解更快的特點，這是深度學習在組合優化問題上的首次應用，旅行商問題是VRP的一種特例，因此，研究人員開始將指針網絡模型應用于VRP的求解。

Nazari等人[45]針對CVRP構建Ptr-Net—REINFORCE模型，該模型是一個end-to-end的深度強化學習模型，通過Ptr-Net進行建模，在構建指針網絡階段，Ptr-Net中的輸入為靜態值（客戶位置）與動態值（客戶需求），其模型結構如圖4 所示。不同于Ptr-Net 在訓練模型時采用監督式方法，使用REINFORCE 算法對模型進行訓練，分別在客戶數為10、20、50、100 的CVRP 數據集上進行了測試，取得了比經典的啟發式搜索算法CW、SW更好的效果。Xin 等人[46]為解決深度強化學習算法在構造解的過程中無法修改以前決策，提出基于REINFORCE算法的分步SW-Ptr-Net 模型和近似SW-AM 模型。該方法有效提升了Ptr-Net 模型和AM 模型[47]對CVRP 的優化效果。

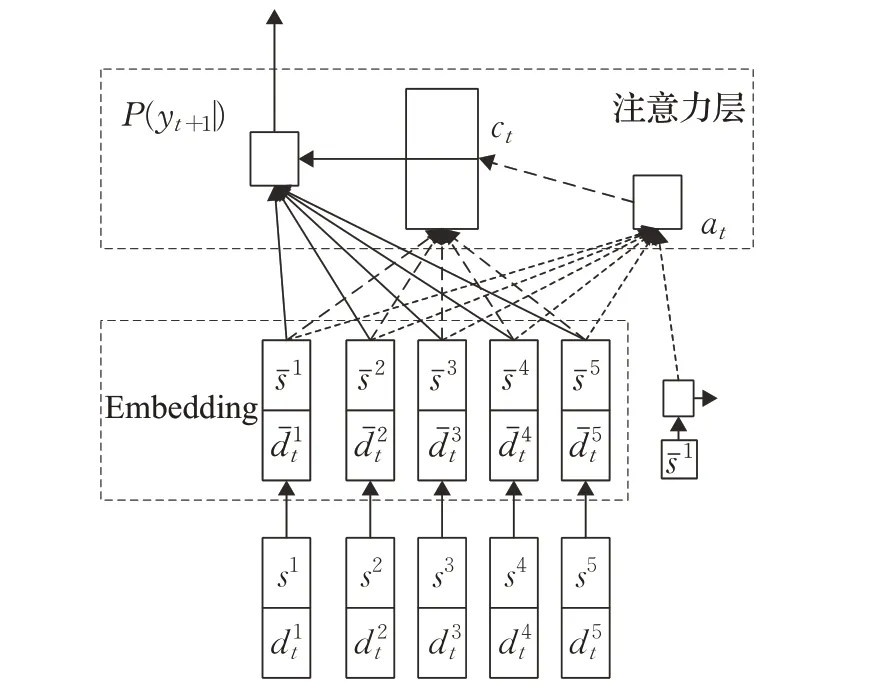
圖4 Ptr-Net-REINFORCE模型示例Fig.4 Example of Ptr-Net-REINFORCE model

（1）基于Ptr-Net的深度強化學習模型總結

Ptr-Net 模型使用編碼器對車輛路徑問題中的初始信息進行編碼得到特征向量，再通過解碼器對特征向量進行解碼，利用注意力機制計算每個客戶節點的選擇概率，從而構造車輛路徑問題的解。所有運用Ptr-Net 模型構造車輛路徑問題的構造過程大致如下：

首先通過Embedding 層把每個客戶節點的地理位置和需求轉化為節點表征向量s，傳入循環神經網絡中得到上下文信息和隱藏層信息。然后通過解碼器對上下文信息進行解碼，利用注意力機制按照隱藏層中的信息和上下文信息得到每個客戶節點的被選概率，每一步都選擇被選概率最大的客戶節點加入解中，逐步構造車輛路徑問題的解。若使用監督式方法訓練模型，需要得到已有最優解的車輛路徑問題訓練集，車輛路徑問題是經典的NP 難問題，因此得到實例的最優解非常困難。且車輛路徑問題均可建模成MDP 模型，使用強化學習算法訓練Ptr-Net 模型是非常合適的。由式（12）可知，REINFORCE 算法是以反向傳播作為參數更新的標準，智能體在探索解空間時，可以不斷提升初始解的質量。因而，當使用Ptr-Net 模型求解車輛路徑問題時，國內外學者常采用REINFORCE算法對模型進行優化。

Ptr-Net 模型這一新型深度神經網絡模型，主要解決輸入時序與位置相關的離散個體組成輸出時序的問題，是求解具有時間序列特性的車輛路徑問題的主要深度學習模型。相較于循環神經網絡處理具有自回歸問題，Ptr-Net 模型對輸入序列長度可變時，直接使用歸一化方式輸出各個客戶節點在當前解碼位置的概率分布。但Ptr-Net 模型復雜度較高，且需要大量的采樣和局部搜索改善Ptr-Net 模型得到的初始解，使模型收斂較慢。

Kool 等人[38]首次將transformer 模型應用到VRP 的求解中，和大多數seq2seq 模型一樣，transformer 的結構也是由編碼器和解碼器組成。在編碼器中作者沒有使用transformer模型輸入時的positional encoding，從而使得節點嵌入不受輸入順序影響，但仍采用經典transformer 模型中的多頭-attention 機制。在解碼器中作者為了提高計算效率并未采用transformer 模型解碼層的多頭-attention 機制，而是只使用一個自-attention 機制。采用加入rollout baseline的REINFORCE算法對模型進行訓練，并在CVRP 和SDVRP 等問題的求解上取得了比基于指針網絡模型更好的效果，且與經典的運籌學求解器LKH3、Gurobi相比求解效果相差無幾。

Falkner 等人[47]針對CVRPTW，提出了JAMPR 模型，該模型由多個編碼器和一個解碼器組成，編碼器采用了self-attention 計算方法，通過加入兩個新的編碼器產生上下文信息以及增強聯合行動空間，解碼器使用transform模型的多頭-attention機制。使用REINFORCE算法對JAMPR 模型進行訓練，模型架構如圖5 所示。在對CVRP-TW 的3 種變體（hard、partly-soft、soft）的實驗中，該模型的優化效果要好于現有的元啟發式算法和基于attention機制的強化學習模型。

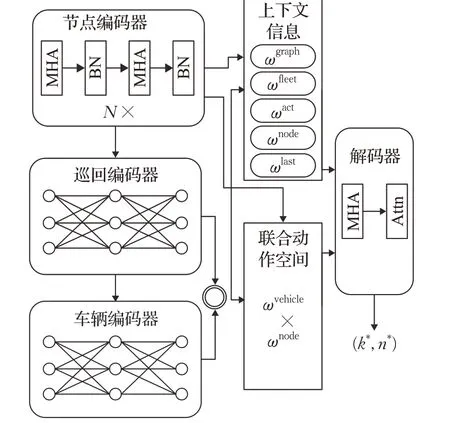
圖5 JAMPR模型示例Fig.5 Example of JAMPR model

Xin 等人[48]提出了一個多解碼器注意模型（multidecoder attention model，MDAM）來訓練波束搜索（beam search）的策略，MDAM 由一個編碼器和多個解碼器組成，編碼器采用和transformer模型相同的多頭-attention機制，每個解碼器采用節點嵌入的方式來產生訪問每個有效節點的概率。使用REINFORCE 算法對JAMPR 模型進行訓練。在對CVRP 和SDVRP 等問題的求解中，相較于所選基準算法該模型的優化效果要更好。為有效地解決具有軟時間窗的多車輛路徑問題（multi-vehicle routing problem with soft time windows，MVRPSTW），Zhang 等人[49]提出了多智能體注意力模型（multi-agent attention model，MAAM），使用REINFORCE 算法對MAAM 模型進行訓練。實驗結果表明，求解速度優于Google OR-tools 求解器和傳統的啟發式算法。Xu 等人[50]以AM模型[38]為基礎構建了具有多重關系的MRAM模型，更好地獲取車輛路徑問題的動態特征。

（2）基于transformer的深度強化學習模型總結

Ptr-Net 模型中因編碼器和解碼器使用循環神經網絡因而存在不能捕獲問題的長程相關性，且模型訓練消耗大量時間，因transformer 模型中的多頭attention 可以提取車輛路徑問題中更加深層次的特征，所以學者們借鑒transformer 模型提出了基于attention 機制提出各類新模型，此類深度強化學習模型僅通過attention機制對輸入輸出的全局依賴關系進行建模，這類模型可以捕獲客戶節點間的長程相關性且有較高的計算效率。但attention 機制需要極大的計算量和內存開銷，所以這類模型的主要改進是通過改變編碼器和解碼器的個數以及編碼方式、解碼方式、注意力機制來實現的。因REINFORCE 算法具有自適應性，可自行調節參數，基于transformer 的各類模型常使用REINFORCE 算法作為訓練模型的算法，但因為REINFORCE 算法方差較大，訓練結果不穩定，研究人員引入帶有基線函數的REINFORCE算法，該訓練算法加快了模型的收斂速度。

Peng等人[51]結合動態attention方法與REINFORCE方法設計了一種AM-D 模型來求解VRP，動態attention方法是基于動態編碼器-解碼器結構來改進的，改進的關鍵是動態挖掘實例的結構特征，并在不同的構造步驟中有效地挖掘隱藏的結構信息，模型架構如圖6 所示。實驗結果表明，在客戶數量為20、50、100 的CVRP 上優化效果均超過了Kool等人[38]提出的AM方法，并明顯減小了最優性差距。Lu等人[52]提出了基于迭代的learn to improve（L2I）框架，算法首先給出一個可行解，運用基于REINFORCE 方法的控制器選擇改進算子或基于規則的控制器選擇擾動算子迭代更新解，經過一定迭代步驟后從所有訪問的解決方案中選擇最優解。對于CVRP，該模型不僅在優化效果上超過了Google ORtools、LKH3等專業運籌學求解器，還是第一個在CVRP上求解速度低于LKH3求解器的強化學習框架，模型架構如圖6所示。

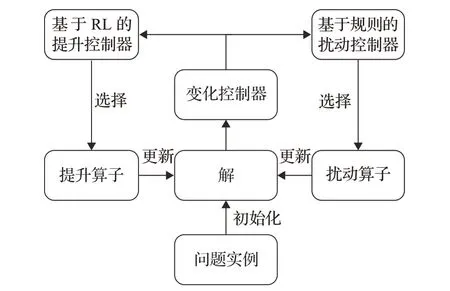
圖6 L2I 模型框架Fig.6 Framework of L2I model

Hottung和Tierney[53]提出神經大鄰域搜索（NLNS）框架對CVRP、SDVRP等問題進行求解，運用基于attention機制的神經網絡對LNS 中的毀壞算子和重建算子進行學習，并用REINFORCE 算法對NLNS 模型進行訓練。實驗結果表明，在CVRP 實例上NLNS 模型與LKH3 性能相當；在SDVRP 實例上，NLNS 能夠在擁有100 個客戶的實例上勝過目前最先進的方法。

（3）強化學習與局部搜索算法結合的模型總結

基于transformer 模型和Ptr-Net 模型求解車輛路徑問題雖然速度較快，但優化效果仍不及專業運籌學求解器。在組合優化問題求解中，局部搜索算法仍然是主流代表算法，局部搜索算法往往涉及到算法參數設置和問題配置，這些都需要算法設計者有高超的算法設計技巧才能保證啟發式算子的效果。學者們基于不同車輛路徑問題的特征和算法結構得到合適的參數和策略，運用強化學習方法對局部搜索策略進行訓練，擴大了局部搜索算法啟發式算子的搜索能力，以此來提高解的質量。目前，求解車輛路徑問題的最優算法就是基于強化學習的局部搜索算法。

4.2.2 REINFORCE算法局限性分析

隨著計算機計算能力不斷增加，REINFORCE 算法已成為深度神經網絡模型解決車輛路徑問題最常用的訓練方法之一。REINFORCE 算法相較于基于值函數的算法，可以表示隨機策略，當策略不定時，可以輸出多個動作的概率分布。但是REINFORCE 算法也存在很多問題，比如數據利用率低、算法收斂速度慢、方差較大導致算法收斂性變差。分析存在以上的原因如下：

（1）數據利用率低

REINFORCE 算法是回合更新的算法，需要完成整個回合，才能更新狀態-動作對。這種更新方式使得整個軌跡的一系列動作被當作整體，若軌跡的收益較低，即使包含一些好的動作，但下次被選的概率仍會下降，使得數據利用率低。

（2）算法收斂速度慢

對于REINFORCE算法，車輛路徑問題中的每個樣本只能被訓練一遍，有些能具有高收益的樣本沒有被重復利用，這不僅浪費計算資源，還增加算法了的收斂時間，使得算法收斂速度慢。

（3）算法收斂性差

在車輛路徑問題中，REINFORCE 算法為控制訓練個體的時間，不可能遍歷所有狀態，只能通過采樣得到大量軌跡，但這樣的做法會造成REINFORCE 算法與環境交互不充分，那些未被選中的動作有可能對應著較高獎勵，因而產生較大方差，導致算法收斂速度變慢。所以經常通過在算法中加入基線函數來避免高方差。

4.2.3 Actor-Critic算法

Actor-Critic 算法是一種基于值方法和基于策略方法相結合而產生的算法。該算法的架構包括兩個部分：Actor 部分是基于策略方法的，通過生成動作并和環境交互，用來逼近策略模型πθ(s,a)；Critic部分是基于值方法的，判定動作的優劣性，并且選擇下一個動作，用來逼近值函數Q(s,a)。Actor 與Critic 之間互補的訓練方式相較于單獨的算法更加有效。策略梯度函數為：

Actor的策略網絡的更新公式為：

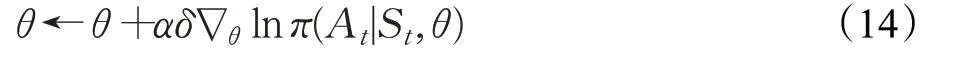
Critic的值函數網絡的更新公式為：

Zhao 等人[55]提出一種改進的Actor-Critic 算法對模型進行訓練，首先通過路由模擬器生成大量VRP 實例用于訓練和驗證，在Actor 網絡的編碼過程中將靜態特征和動態特征分別編碼，在基本attention機制[38]中，模型對輸入序列的順序很敏感。為了克服這個問題，采用了圖嵌入的方法，Critic 網絡由一個Simple 網絡和一個Actor網絡組成，為加快模型收斂速度，還借鑒了圖像字幕[56]中的Self Critic 思想，據此構成了Adaptive Critic網絡，網絡架構如圖7所示。新的Actor-Critic模型在客戶點數分別為20、50 和100 的3 個數據集上進行測試。實驗結果表明，該模型找到了更好的解決方案，同時實現了5到40倍的加速。還觀察到，與其他初始解決方案相比，將深度強化學習模型與各種局部搜索方法相結合，可以以更快的求解速度得到解。

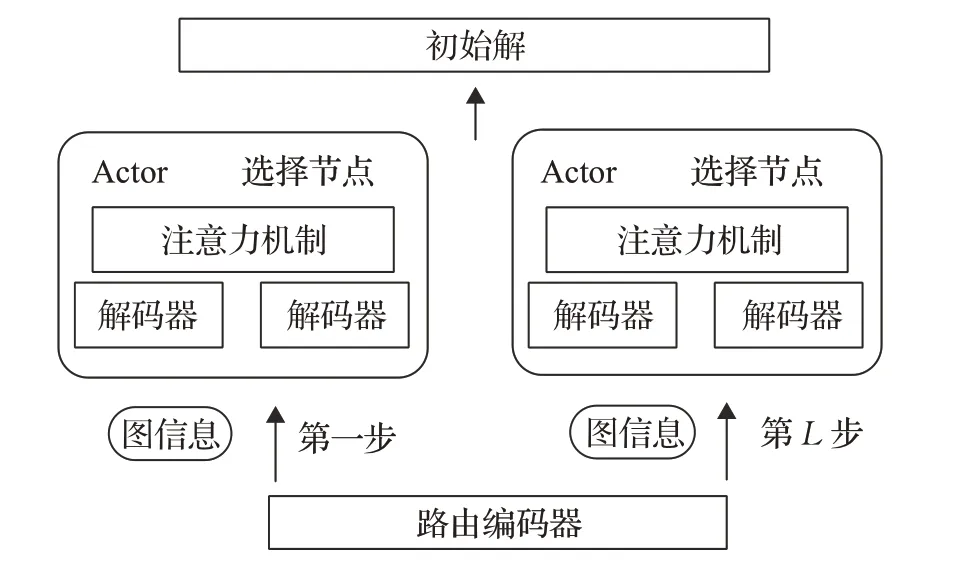
圖7 Adaptive Critic 網絡示例Fig.7 Example of Adaptive Critic network

在日常生產生活中，一個客戶可能總是有他自己的送貨點，比如同城快遞服務[57]和拼車服務[58]，而不是像VRP那樣為所有客戶共享一個倉庫。所有這類VRP可描述為提貨和交貨問題（pickup and delivery problem，PDP）。Li 等人[56]提出了一種基于異構attention 機制的編碼器-解碼器模型，其編碼層在多頭attention注意力方法中加入了異構attention 方法以期更早得到優先級較高的關系，采用Actor-Critic算法對該模型進行訓練。在PDP 求解中該模型的優化效果要好于傳統的啟發式算法。Gao 等人[57]提出了基于圖注意力網絡的模型用去求解VRP、CVRP。該模型的編碼器是由一個graph attention network 組成，模型首先對每個客戶位置進行編碼得到每個客戶頂點的邊緣嵌入和頂點嵌入，在通過attention機制計算出每個客戶被選擇的概率。解碼器采用和Ptr-Net一樣的架構，為VLNS算法的破壞算子提供一個節點子集作為移除候選。依然采用Actor-Critic 算法對該模型進行訓練。

當VRP、CVRP、CVRPW 等問題的規模較大時（多于400 頂點），該模型優于傳統啟發式算法和現有求解VRP的深度強化學習模型。

強化學習與圖神經網絡結合的模型總結：車輛路徑問題是典型的具有圖結構的組合優化問題，因圖神經網絡能夠有效求解具有圖結構的問題，所以有學者把圖神經網絡應用到了車輛路徑問題的求解中，運用圖神經網絡求解車輛路徑問題的構造。

過程大致如下：將車輛路徑問題建模為圖G=(V,E)，其中V代表節點集合，E代表邊集合。圖神經網絡根據用戶節點Vi本身的二維空間位置和需求、邊的特征，以及節點Vi鄰居節點的二維空間位置和需求對節點Vi特征向量進行更新，從而得到每個節點的特征向量。為加快模型收斂，研究人員通常把圖神經網絡求得的用戶節點的特征向量加入transformer 模型和Ptr-Net 模型的編碼器中，在通過attention 機制計算出每個客戶被選擇的概率。因為Actor-Critic 算法融合了基于值的算法和基于策略的算法的優點，即可解決連續動作空間問題，還能進行單步更新從而加快學習速度，所以在圖神經網絡中常使用Actor-Critic 算法訓練模型。

4.2.4 Actor-Critic算法局限性分析

Actor-Critic 算法是目前最為流行的強化學習算法之一，結合了基于值算法和基于策略算法的優點，既能應用于連續動作空間，有能進行單步更新。但仍然存在一些問題，比如學習效率低，收斂速度慢。分析存在以上問題的原因如下：

（1）學習效率低

Actor-Critic 算法中涉及到Actor 網絡和Critic 網絡兩部分，Actor網絡基于概率選擇動作等價于策略函數，Critic網絡等價于價值函數。Actor-Critic算法每次更新都會涉及到這兩個深度神經網絡，而且每次都在連續狀態中更新參數，參數更新時有很強的相關性。導致算法學習效率低。

（2）收斂速度慢

Actor-Critic算法中Critic網絡收斂速度慢，若Critic網絡不收斂，那么它對Actor網絡的評估就不準確，導致Actor網絡難收斂，使得Actor-Critic算法收斂速度慢。

4.2.5 Advantage Actor-Critic算法

Advantage Actor-Critic（A2C）算法又稱同步優勢Actor-Critic算法是Mnih等人2016年提出的。在Actor-Critic 算法中Critic 網絡輸入Q值來對策略梯度進行計算，但這種計算方式存在高方差的問題，從而可以引入Baseline 的方式減小梯度使得訓練更加平穩，通過這種改進就能得到A2C 算法。A2C 算法的策略梯度函數為：

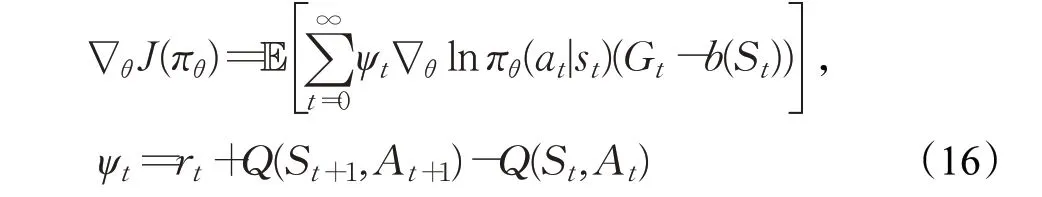
A2C算法的優勢函數為：

A2C 算法將Critic 網絡對Q值的估計改為對優勢函數的估計，估算每個決策相較于平均值的優勢。A2C算法的整體架構與Actor-Critic算法類似，只是在其基礎上加入了并行計算的能力，即整個個體由一個全局網絡和多個并行的工作體（worker）組成，每個工作體都包括一個Actor-Critic網絡。

Vera和Abad[58]針對固定車隊規模的容量受限多車輛路徑問題（capacitated multi-vehicle routing problems，CMVRP），提出了基于Attention 機制的Seq2Seq模型，采用A2C 算法對模型進行訓練，與經典的啟發式算法SW 和CW 相比該模型生成的解具有更低的標準差。

A2C算法使用一個優勢函數作為評價標準，這個優勢函數用來評價當前所選動作與所有動作平均值之間的差值，從而降低了AC 算法所產生的誤差。但運用A2C算法求解車輛路徑問題時，智能體在環境訓練中的穩定性較差。

4.3 基于動態規劃求解VRP分析對比

基于無模型強化學習方法求解VRP 的對比結果見表3。

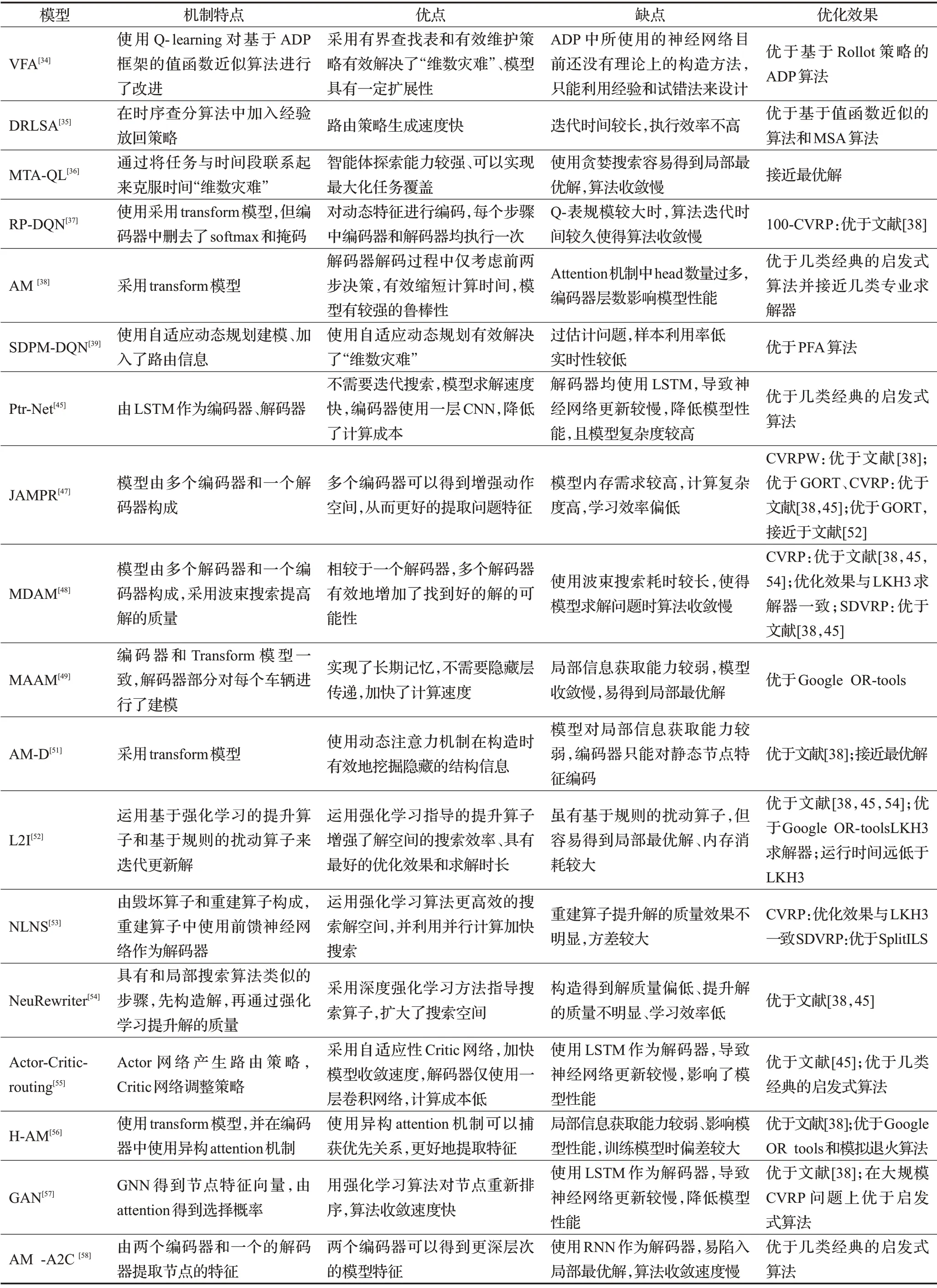
表3 無模型方法求解車輛路徑問題對比Table 3 Comparison of approaches of model-free applied to VRP

5 強化學習算法總結分析

近年來，強化學習在車輛路徑問題求解中涌現了很多優秀的算法，在應用過程中這些算法有自己的優勢，但也暴露出一些自身局限性，將上述內容進行總結分析，如表4所示。

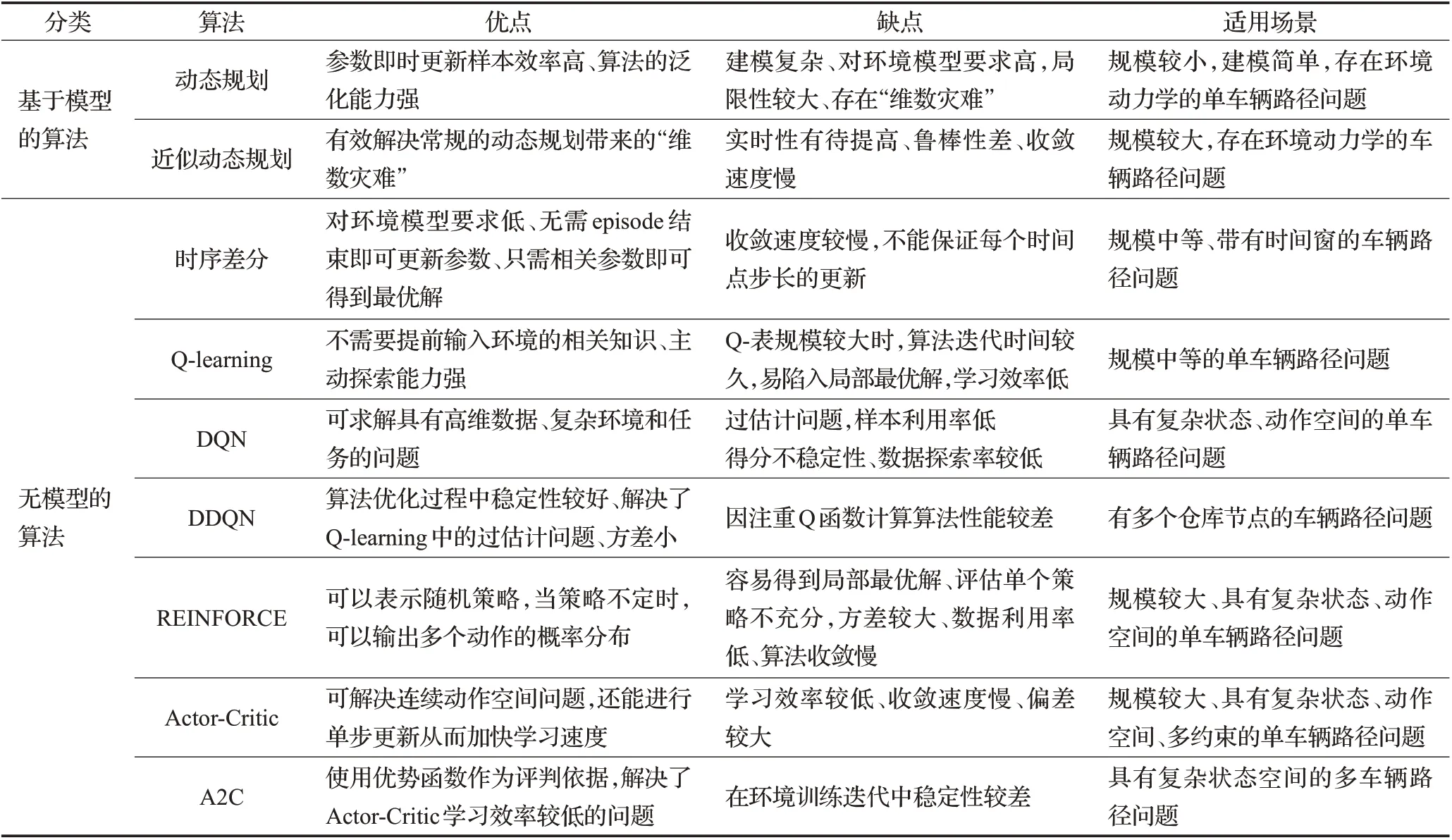
表4 強化學習總結Table 4 Summary in reinforcement learning

基于模型的強化學習算法求解車輛路徑問題時需先構建MDP模型，智能體通過與環境的不斷交互，智能體對數據的利用率較高。為增強求解問題的實時性，使用rollout框架對初始策略進行迭代更新，逐步逼近最優解。近似動態規劃中使用自舉采樣法訓練神經網絡，自舉采樣得到的數據不是獨立同分布的，這樣的采樣方式使模型穩定性降低。

現在的使用深度強化學習模型解決車輛路徑問題時主要的創新點是對深度神經網絡架構的設計上，即設計更加契合車輛路徑問題的數據結構，主要包括像Ptr-Net 模型和transform 模型這種把問題建模為序列形式的輸入，然后基于各類attention機制對客戶節點的選擇優先級進行排序；因車輛路徑問題天然是圖結構，可基于圖神經網絡和基于圖神經網絡的attention 機制提取車輛路徑問題的特征。通過以上方法得到局部解后以自回歸的方式擴展得到最優解。因為監督式學習方法不適用與組合優化問題，學者們采用具有反向學習能力的強化學習算法訓練模型。深度強化學習模型求解速度遠超傳統的啟發式算法，模型泛化能力較強。

強化學習算法的優勢是智能體通過和環境進行交互可以得到最優策略，從而具備解決大規模復雜組合優化問題的可能性，但其也存在著算法執行時間過長、模型不易收斂等局限性。因此，可用其他啟發式算法和強化學習融合，主要是使用強化學習算法對啟發式搜索算子進行學習，加快求解速度，提高解的質量，相較于人工設置搜索策略，強化學習算法可以擴大搜索空間和提高搜索策略效率，具有較強的優化能力。

6 結論與展望

本文旨在對近年來基于強化學習求解車輛路徑優化問題的各類算法進行較為全面的綜述，重點分析了各類強化學習算法的機制特點和優劣性。如今在VRP的求解中各類深度強化學習模型不斷涌現，本文對這些模型的特點和優化效果進行了總結。基于模型的強化學習算法必須對問題進行建模，但往往車輛路徑問題建模過程與現實環境總有差距。在基于編碼器-解碼器的transformer 模型和Ptr-Net 模型以及圖神經網絡中強化學習算法都是作為訓練模型的算法出現，選擇強化學習算法時目的性不強。且強化學習自身存在較強的探索和利用困境，個體不僅要學習以前樣本中的動作，還要對未來可能帶來高獎勵的動作進行探索，但車輛路徑問題是高度復雜的大型問題，強化學習常用的探索策略常常失效，探索策略的可擴展性較差。強化學習算法常因為經驗樣本只被采樣一次或隨著經驗的積累，同一個樣本被多次抽樣的概率越來越小，從而導致樣本的采樣率較低。計算機本身計算能力也限制了強化學習算法的效果。且目前基于強化學習求解車輛路徑問題的模型，主要都是對客戶節點小于100的問題進行求解，很少有作者對大規模車輛路徑問題進行求解。因此，未來基于強化學習模型求解車輛路徑問題的工作可從以下方面展開：

（1）建立更小誤差的環境模型。對于有模型的強化學習算法，精確的環境模型可以減少個體和環境的交互，可以通過模型仿真生成大量樣本數據，使得算法快速學習。通過更加科學的方式定義參數，減少人為設定引起不確定性，可增強模型的可靠性。但當數據量較少的時候，學到的模型誤差較大，且現實生活中的車輛路徑問題的環境動力學較為復雜，從而使得建立精確模型更為困難。

（2）提高數據采樣率。針對無模型的強化學習算法數據采樣率低的問題，可以重新設計采樣方法，使用離軌策略設計并行架構進行學習；針對有模型的強化學習算法采樣率低的問題，可以將模型誤差納入模型設計中，從而提高數據采樣率。

（3）設計更加高效的模型。目前求解車輛路徑的深度強化學習模型中，運用深度神經網絡直接求解得到初始解的質量較差，大多數模型都需要與其他方法結合提升解的質量，使得求解時間變長。因而，未來可以對神經網絡的理論基礎進行深入研究，設計更加高效的深度網絡結構和表示方法，得到更加高效模型。尤其是圖神經網絡與新型注意力機制結合是未來的重點研究方向之一。

（4）選擇更加合適模型訓練算法。目前基于編碼器-解碼器求解車輛路徑問題的模型，常直接選用REINFORCE算法、Actor-Critic算法等常規的強化學習算法，不同類型的車輛路徑問題優化目標不同，能有效解決復雜問題的多智能體強化學習和分層強化學習尚處在探索階段，如何選用更新高效強化學習算法作為模型的訓練方法，對提升模型性能至關重要。這也是一個重要的改進方向。

（5）提升模型穩定性。現有的深度強化學習模型一旦訓練完成，就可以求解同類型的問題，泛化能力較強，但是優化效果無法保證，局部搜索算法可移植性差，但優化效果較好。因此，運用更加高效的強化學習算法提升一些經典局部搜索算法的求解速度，是未來重要的研究內容。

（6）提高解決現實工程問題的能力。車輛路徑問題和現實生活息息相關，通常具有多約束、動態變化的特點，當前的強化學習算法和深度強化學習模型可以求解的車輛路徑問題約束較少，規模較小。深度學習模型的最大優勢就是可以在大規模問題上有良好表現，因此，設計更加契合車輛路徑問題的深度神經網絡架構是有效求解大規模、復雜車輛路徑問題的方法之一，這也是未來可著重研究的方向。

強化學習已成為熱門的組合優化問題求解方法之一，但就目前而言，基于強化學習求解車輛路徑問題的算法模型并不具備真正的工程應用能力。隨著研究不斷深入和理論不斷創新，強化學習將會和其他最新先進技術結合，讓強化學習在車輛路徑問題求解中發揮更大作用。