基于ABAQUS的車輛盤形制動系統仿真分析

朱新榮，彭俊，徐祥文

（中車南京浦鎮車輛有限公司，南京 210031）

0 引言

隨著高速鐵路技術的發展，軌道車輛的運輸效率大幅提高，促進了我國經濟的發展[1]。隨著列車運行速度的不斷提高，對列車運行的安全性和乘客乘坐的舒適性要求也在不斷提高。制動系統是保障列車穩定、安全運行的保障之一，因此對列車制動要求也不斷提高[2]。在制動的過程中，制動系統會產生振動和噪聲，會嚴重影響列車運行的安全性、列車疲勞壽命、旅客的乘坐舒適性，產生的噪聲還會對鐵路沿線居民造成噪聲污染[3]。

李棟等[4]建立CRH2拖車盤形制動系統的摩擦耦合有限元模型，對制動過程中盤形制動系統的運行穩定性和自激振動的瞬態動力學進行分析，同時對影響盤形制動系統噪聲的因素進行了研究，研究表明，隨著摩擦因數、閘片彈性模量的增大，制動產生的噪聲頻率增大，隨著制動盤彈性模量增大，制動產生的噪聲頻率先降低后增大。丁旺才等[5]建立了干摩擦的單自由度盤形制動系統動力學模型，計算了系統發生顫振運動的臨界速度，并討論了阻尼比、動摩擦因數及最大靜摩擦因數與動摩擦因數之差對臨界速度的影響。曾京[6]建立了并聯的兩自由度顫振模型，分析了不同制動速度、不同制動壓力及不同阻尼對顫振的影響。文武[7-9]使用有限元軟件建立了包括制動盤、閘片、閘片托、制動杠桿和杠桿托等部件的全尺寸鐵路車輛盤形制動系統有限元模型，利用有限元復特征值方法分析制動系統摩擦噪聲的技術，提高了運用有限元復特征值分析制動系統摩擦噪聲的效率。

本文利用ABAQUS建立了車輛盤形制動的有限元模型。利用模態分析方法，分別對制動盤、摩擦片和盤形制動耦合系統進行模態分析。得到了制動盤、摩擦片和盤形制動系統的模態頻率與振型。分析了盤形制動系統產生噪聲的原因。

1 盤形制動系統模型建立及網格劃分

1.1 盤形制動系統模型

盤形制動裝置（如圖1）主要由液壓制動缸、制動閘片、制動盤、夾鉗臂及連桿裝置組成，其中制動閘片和制動盤是盤形制動系統最主要的組成部分。基于三維實體建模軟件SolidWorks建立了盤形制動系統模型，如圖2所示。完整的盤形制動系統比較復雜，為了提高計算效率，建模時可以簡化盤形制動系統，只考慮由制動盤和制動閘片構成的摩擦副。制動閘片和制動盤的材料屬性如表1所示。

表1 盤形制動系統材料屬性

圖1 盤形制動裝置

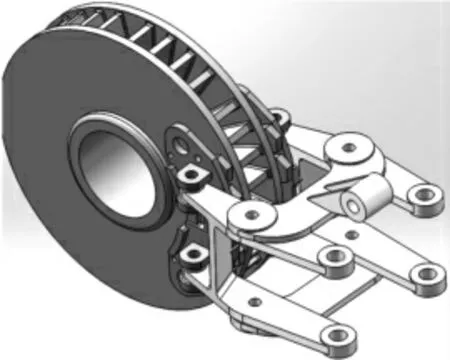
圖2 盤形制動系統模型

1.2 網格劃分

對盤形制動系統進行有限元分析需要將盤形制動系統離散成若干個有限元單元，合理的有限元單元類型、單元形狀、單元大小和單元數量是得到正確結果的前提條件。因此，為了高效、準確地求解，在劃分網格的過程中需要合理選擇網格的類型，設置合適的網格數量。針對盤形制動系統模型，在節省計算時間和保證計算精度的前提下，考慮在非接觸區采用比較大的網格，在接觸區采用比較小的網格。綜合考慮上述因素，采用四面體網格對盤形制動系統進行網格劃分，并將制動盤劃分為26 596個單元，將制動閘片劃分為53 210個單元。

2 盤式制動特性分析

將建立好的盤形制動系統導入到ABAQUS中，利用ABAQUS軟件對車輛盤形制動有限元模型在約束了邊界條件的情況下進行模態分析，得到各零件在邊界條件下的固有振動頻率，由于有限元中模態分析的本質是求矩陣，所以“階數”就是指特征值的個數。將特征值從小到大排列就是階次。實際的分析對象是無限維的，所以其模態具有無窮階。但我們在分析一個系統的過程中，往往只關注對系統起主導作用的模態，忽略對系統影響比較小的模態，對制動盤、制動閘片及它們的綜合模態的分析，本文只考慮其前30階模態并對其進行分析。

2.1 制動盤模態分析

將建立好的制動盤的有限元模型導入到ABAQUS中，進行仿真分析，得到制動盤的固有頻率，制動盤前30階模態振型如表2所示。選取第10 372號節點，這個點是發生制動噪聲的關鍵。圖3給出了10 372號節點前30階模態及其響應位移幅值曲線。從圖中可以看出，第3階、第7階、第10階、第16階、第18階、第21階、第25階、第27階模態振型的響應位移比較大。尤其是第3階模態振型的振幅達到了0.96 mm，此時對應的頻率f=1146.6 Hz。如果制動盤受到外界激勵的頻率接近上述8個頻率時，將會引起制動盤的大幅振動。

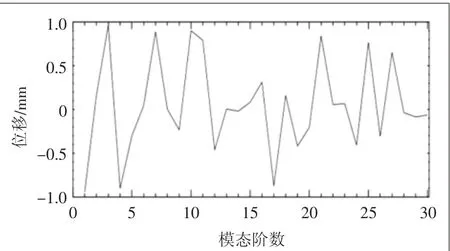
圖3 節點10 372前30階模態及其響應

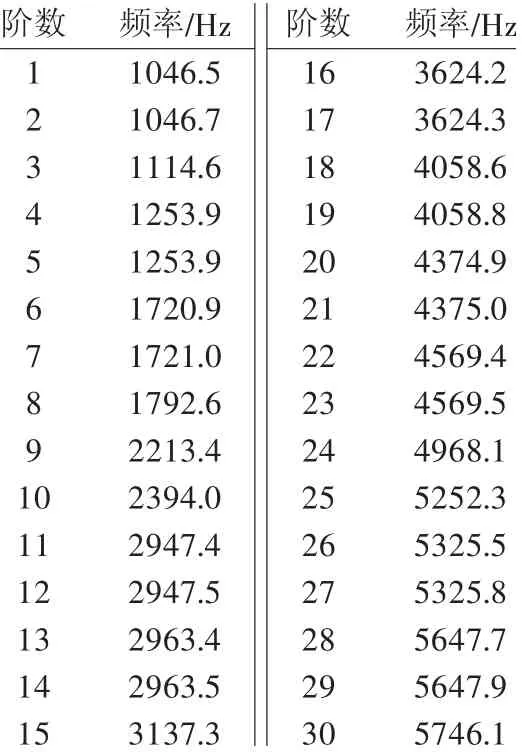
表2 制動盤前30階模態頻率

圖4給出了第3階、第7階、第10階、第16階、第18階、第21階、第25階、第27階模態陣型圖。從圖中可以看出，制動盤容易在低頻階段產生共振，并且沿著制動盤軸向發生較大變形。當列車在制動的過程中，制動盤的軸向變形會劣化制動盤與閘片之間的接觸，從而影響制動效果。

2.2 制動摩擦片模態分析

將建立好的制動閘片的有限元模型導入到ABAQUS中，通過Lanczos方法提取了制動閘片的前30階模態，制動閘片前30階模態振型如表3所示。選取制動閘片中心出的節點48 981進行分析，節點48981前30階模態及其響應曲線如圖5所示。從圖中可以看出，在第2階、第3階、第6階、第12階、第14階、第18階、第22階模態處位移比較大。其中，在第2階模態振型對應的振幅最大，達到了0.86 mm，此時對應的頻率f=1.169 78×10-4Hz。當制動閘片受到的外界激勵振動頻率接近上述7個頻率時，將會引起制動閘片的大幅振動。

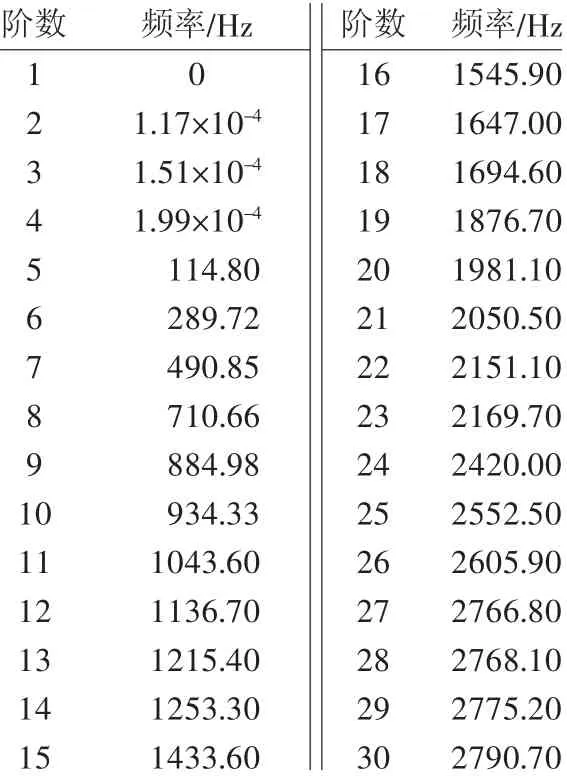
表3 制動閘片的前30階模態頻率

圖6給出了制動摩擦片第2階、第3階、第6階、第12階、第14階、第18階、第22階模態振型。從制動摩擦片的模態振型圖可以看出，制動摩擦片的邊緣變形量最大。

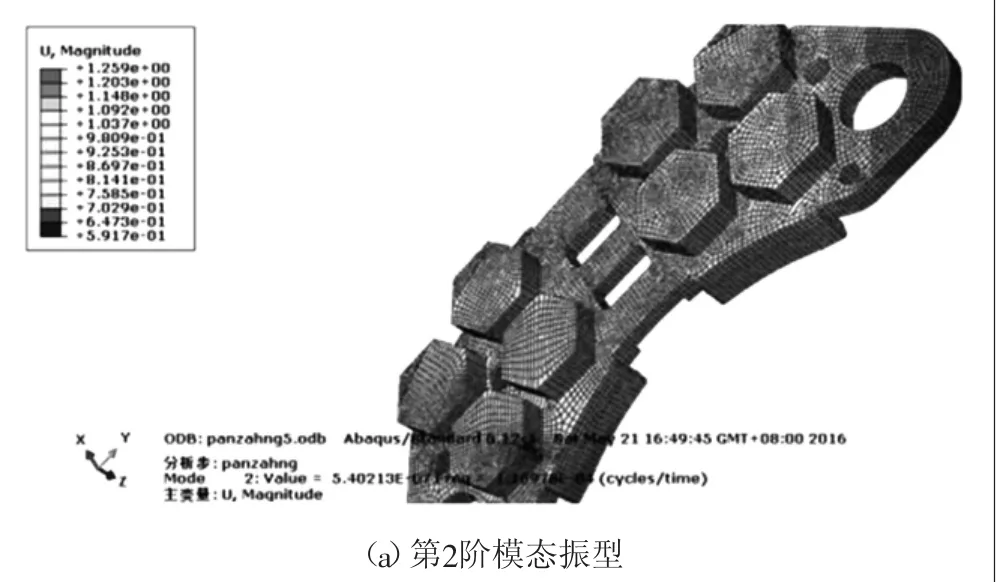
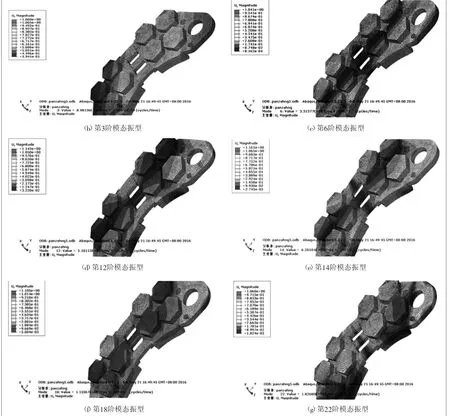
圖6 制動摩擦片模態振型

2.3 盤形制動過程綜合模態分析

由于列車在制動的過程中，制動盤和制動閘片是配合后一起工作的，所以再把制動盤和閘片進行裝配，對制動閘片和制動盤進行約束，限制制動盤3個方向的平移、2個方向的旋轉，釋放軸向轉動的自由度；對制動閘片沿軸向的平動進行約束。對約束好的盤形制動系統進行模態分析。

盤形制動時，制動盤與制動閘片發生了周向共振，產生了噪聲。因此，提取了盤形制動系統周向共振的頻率，其前30階模態頻率如表4所示。

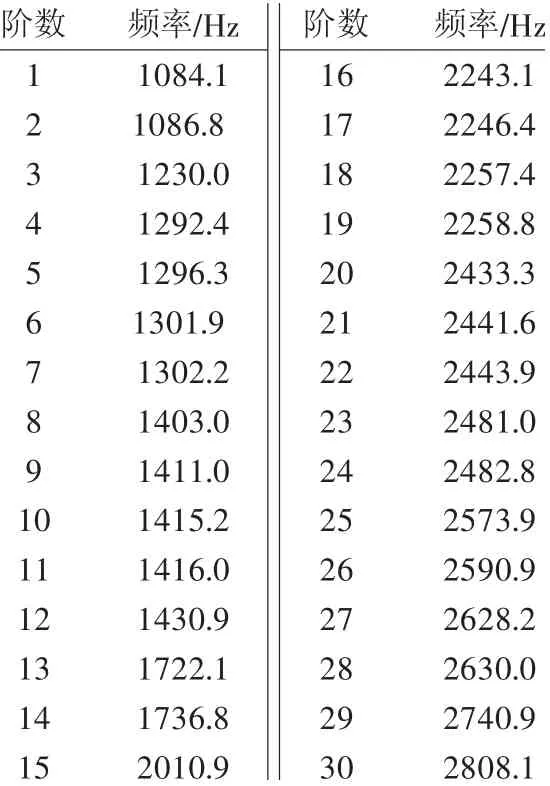
表4 盤形制動系統周向共振頻率

圖7給出了盤形制動過程中第4階、第13階、第14階、第15階、第16階、第21階、第29階模態振型。從盤形制動系統的模態振型圖可以看出，第29階模態振型為制動盤與制動閘片的周向共振振型，此時制動盤與制動閘片發生周向共振，對應的共振頻率為2740.9 Hz。

圖7 盤形制動過程綜合模態振型

3 結論

基于三維實體軟件SolidWorks建立了軌道車輛盤形制動系統，并利用ABAQUS建立了車輛盤形制動的有限元模型，分別對制動盤和摩擦片進行模態分析。得到了制動盤、摩擦片和盤形制動系統的模態頻率與振型。研究表明，當制動盤與制動片發生周向共振時，制動過程便會產生噪聲，共振頻率為2740.9 Hz。