基于社團檢測算法的固件二進制比對技術
肖睿卿 費金龍 祝躍飛 蔡瑞杰 劉勝利
(數學工程與先進計算國家重點實驗室 鄭州 450001)
二進制比對是逆向分析領域的重要分支,其主要目的是通過比對不同程序的二進制代碼,確定不同程序間的相似關系,如:函數相似性、文件相似性[1].該技術可用于固件比對[2]、補丁比對[3]、軟件抄襲檢測[4]、惡意軟件檢測[5]、漏洞分析[6]等領域.
固件比對屬于二進制比對范疇,但固件較普通軟件而言,規模更大.現有的二進制比對方法主要依靠函數語義特征提取(如三元組[7]),而后直接從待比較程序中依據特征序列(或特征序列映射后的值)挑選匹配函數.此類方法可以應用于固件比對,但由于固件的函數數量較多,因此,固件中語義特征相似甚至相同的情況頻繁出現,導致函數比對時目標函數數量較大且包含大量語義特征相近的函數,給基于語義特征進行固件比對帶來挑戰.為解決這些問題,降低函數比對過程中的目標函數數量,本文根據復雜網絡相關理論,研究了基于社團檢測的固件比對方法.
本文的研究目標是設計臨近版本固件的函數對應關系構建方法,旨在通過此法找到舊版本固件函數在新版本固件內的對應函數(亦稱函數匹配),以對固件的補丁比對提供支撐.
本文的主要貢獻有3個方面.
1) 基于網絡科學理論中的ER隨機圖模型,分析了用社團檢測算法指導固件比對的可行性.從目前梳理的文獻來看,這是首次在二進制比對領域對函數調用圖的性質進行分析,并應用復雜網絡相關理論指導比對工作.
2) 提出了基于社團檢測的固件比對方法.包括2部分:基于固件函數調用圖的社團檢測和匹配方法;基于社團匹配的函數匹配算法.前者設計了函數調用圖壓縮算法,提出了固件社團匹配算法.后者優化了函數相似性計算方法,設計了函數誤匹配的修正方法.
3) 使用本文方法形成原型系統,通過實驗驗證可行性,確定合理參數,對樣本固件進行二進制比對,并與Bindiff5[8]的匹配結果進行比對.實驗表明,本文方法可以提升Bindiff比對結果5%~11%的準確率.
1 概 述
1.1 二進制比對技術
近些年,二進制比對領域的研究趨勢傾向于固件比對、補丁比對和跨指令集比對.相關研究具有3個特點:
1) 多數研究者將工作重心放在了尋找函數刻畫方法上,以此提高二進制比對的準確率.包括靜態提取函數語義信息和動態執行獲取輸入輸出對等多種思路.
其中,文獻[9]從函數控制流圖(control flow graph, CFG)提取特征向量,再使用譜聚類構建碼本.而后計算函數與各個質心的編輯距離以構建新的特征向量,以此來刻畫函數.通過這種函數刻畫方法,完成固件比對工作.文獻[10]在文獻[9]的基礎上開展工作,主要通過深度學習,將函數調用圖(function call graph, FCG)中與目標函數有調用關系的函數的特征向量整合入目標函數的特征向量.此法能夠將FCG的局部網絡信息整合入函數節點,使得函數特征來源更全面.文獻[11]將二進制程序切割為比函數更小的代碼片段,通過對代碼片段的語義進行相似性分析,再將相似性分析擴展到更大范圍.文獻[12]同樣使用控制流圖來刻畫函數,但其選用特征強調了計算經濟性,依據計算經濟性的高低逐個進行特征的提取和使用,并以此來縮小匹配函數的搜索范圍,避免從全局來進行搜索.文獻[13]利用條件操作行為和系統調用信息提取函數簽名,以此實現兼容不同指令集的函數刻畫.文獻[14]使用子圖匹配來尋找克隆函數,并使用自適應局部敏感散列(locality sensitive hashing, LSH)來提高搜索效率.文獻[15]首先使用基本塊和執行路徑的最大公共子序列進行函數匹配,而后利用匹配函數的鄰居關系擴展匹配.文獻[16]通過提取條件公式作為函數的高級語義特征,用以進行漏洞檢索.文獻[17]通過識別函數的參數和間接跳轉目標,并模擬執行函數,以提取語義簽名度量函數的相似性.文獻[18]對于給定二進制程序的原始版本和已修補的版本,找到已修補的函數并標識可能包含安全補丁或非安全補丁的功能更新.而后,通過對差異點語義分析以識別安全補丁,并使用污點分析來總結模式.文獻[19]通過計算和匹配反匯編的結構和句法,為二進制代碼指紋識別提供一種準確且可擴展的解決方案,可用于二進制比對.文獻[20]將二進制函數分解為可比較的片段,通過執行函數片段重優化降低語義分析的強度,再通過簡單的語法比較來找到等效的片段.文獻[21]從CFG、指令特征、統計特征等方面為庫函數生成簽名.并設計了一種新穎的數據結構來存儲此類簽名以實現針對目標函數的高效匹配.文獻[22]提出了基于系統調用切片段等效的檢查方法,通過識別細粒度語義相似性和執行軌跡間差異實現此法.文獻[23]利用內存模糊測試進行二進制代碼相似性分析,通過收集各種程序行為的痕跡,根據2段代碼行為軌跡的最長公共子序列,計算它們的相似性得分.文獻[24]利用操作碼頻率提取函數的語法特征;利用控制流圖隨機游走提取函數語義;將z分數(z-score)應用于規范化指令,以提取函數內指令的行為.
2) 隨著深度學習相關技術的興起,部分研究者選擇了不直接提取函數特征的策略,嘗試利用神經網絡規避傳統特征提取帶來的信息丟失的情況.
其中,文獻[25]僅靠指令序列和長短時記憶網絡(long short-term memory, LSTM)實現了跨平臺比對功能.主要通過將不同的匯編轉化為特征值,而后利用LSTM訓練以完成不同指令集指令對應關系的構建.文獻[26]使用神經網絡逐字節地提取函數特征.根據函數調用圖,提取函數間和模塊間(導入函數等)特征.然后,基于這3個特征計算距離用于相似性分析.文獻[27]首先提取基本塊特征構造函數的特征向量.然后,利用神經網絡將其轉化為函數的嵌入向量.最后,基于余弦距離來測量2個二進制函數的相似性.文獻[28]使用神經網絡同時學習基于匯編代碼的詞匯語義關系和向量表示.僅輸入匯編代碼以尋找并合并語義關系,根據語義判定函數相似性.文獻[29]提出了一種基于自注意神經網絡的函數嵌入模型.通過將嵌入向量與具體指令關聯,直接用作模型輸入,而后依據輸出向量進行相似性分析,以表示函數相似性.
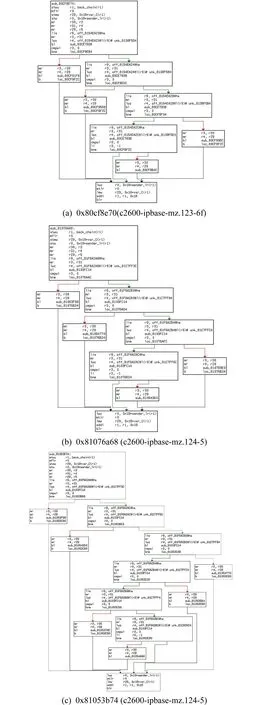
Fig. 1 Three CFGs of Cisco’s firmwares with two versions
3) 部分研究者意識到二進制比對過程中,選擇待比對目標函數帶來的開銷,嘗試用不同方法過濾目標函數.
其中,文獻[30]提出了一種內聯方法用來捕獲函數完整的語義,同時,為了解決目標函數數量巨大的情況,引入了3種過濾器過濾目標函數,包括相同庫函數、同類型庫函數、相似指令類型和函數簽名.文獻[31]首先基于1組異類特征(包括:指令語義特征、結構特征、統計特征)濾除不相似的函數;再根據不同的執行路徑進一步過濾剩余函數;最后基于模糊圖匹配識別候選函數.
從上述3個特點不難發現,現有二進制比對領域的相關技術若應用于固件比對,仍具有一定缺陷:
1) 現有研究較少研究過濾器,過濾目標函數主要依靠函數自身的特征向量的相似性.然而,同一固件中往往存在若干完全一致的函數,將導致固件比對過程中的誤匹配.以圖1為例,其中圖1(a)(b)所示函數同構但不匹配,圖1(a)(c)函數匹配但不同構.這些誤匹配會隨著傳播算法擴大誤匹配范圍.
2) 函數相似性判別較為依賴庫函數、導入表等信息,部分研究依賴于動態調試,而固件分析往往不具備前文的3個特點.
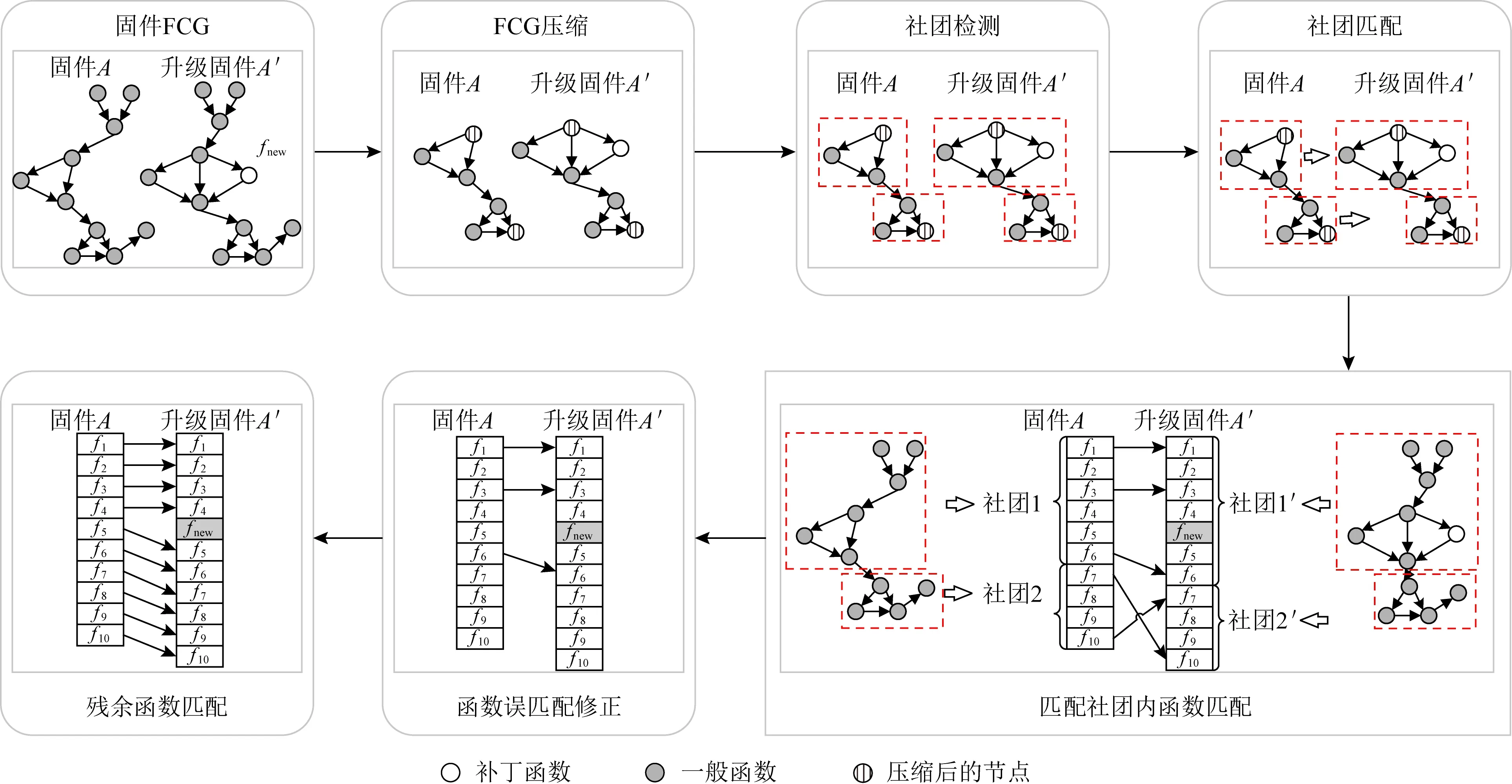
Fig. 2 Method overview of this paper
3) 實驗驗證對象函數規模較小且偏向于開源程序,不足以暴露研究成果在固件比對領域的缺陷.現有二進制比對的研究中,收集的軟件普遍較小,甚至文件大小不足10 KB.部分關于固件的研究,由于固件可以解包,實際分析的文件也相對較小.但,固件中存在以Cisco IOS為代表的一體化固件,此類固件不可解包,文件大小常達到100 MB以上,函數數量幾十萬.且固件由于廠商的安全性考慮,基本不提供開源代碼用于研究.此類場景下,依賴開源代碼的分析研究無法適用.
1.2 社團檢測技術
社團檢測屬于網絡科學范疇,其主要目的是找到網絡中的社團.社團是網絡的子圖,由網絡中的1組節點(頂點)及組內節點間的連邊構成,組內節點之間的連接較稠密,而節點與組外節點的連接較稀疏[32].
由于對社團的稠密與稀疏沒有定量的劃分,因此,不同研究者設計了多種社團檢測算法.
其中,文獻[33]提出了模塊度的概念用以衡量社團劃分標準.文獻[34]提出了基于模塊度和貪婪算法思想的社團檢測算法CNM.文獻[35]提出了一種層次化的社團檢測模型,可用于加權網絡,稱為BGLL算法(亦稱Louvian算法).
此外,文獻[36-37]提出了基于派系過濾的社團檢測算法.文獻[38]提出了連邊社團檢測算法,通過邊的唯一社團屬性,以邊為單位,構造樹圖,以此完成社團檢測.
1.3 方法概述
針對1.1節中指出的問題,本文使用BGLL算法對固件的FCG進行社團檢測,將函數劃入不同的社團,以此引導函數過濾,彌補傳統過濾器的不足;此外,本文增補了立即數和偏移量特征用以提升函數比對準確率.
本文方法的流程包括2個步驟,如圖2所示.
1) 固件社團檢測與匹配.包括固件FCG壓縮、社團檢測與社團匹配.
2) 函數匹配.包括匹配社團內函數匹配、社團內函數誤匹配修正、殘余函數匹配.
2 可行性分析
文獻[32]指出,社團結構是復雜網絡一個極其重要的特性,針對不同類型的大規模復雜網絡,人們提出了很多尋找社團結構的算法.由此可以看出,社團檢測算法主要的工作場景是大規模復雜網絡.
本文要使用網絡社團檢測技術用于引導固件函數過濾,就有必要對固件FCG的性質加以分析,以確定使用此技術是否恰當.如果FCG規模與結構過于簡單,使用社團檢測算法可能意義不大.例如:對于完全圖而言,其結構過于規則,并無使用此法的必要.
直觀而言,從固件的FCG中一般可以直接觀察到其復雜程度,甚至社團的存在.如圖3所示,該圖展示了固件c3725-ipbase-mz.124-5的函數調用關系,函數數量20余萬.雖然調用圖存在多個連通片,但依舊可以觀察到最大連通片,其節點規模龐大、調用關系復雜,且有若干社團存在.但理論分析依然是必要的.
在本節中,我們將對樣本固件FCG的性質進行分析,以確定社團檢測算法用于固件比對的可行性.
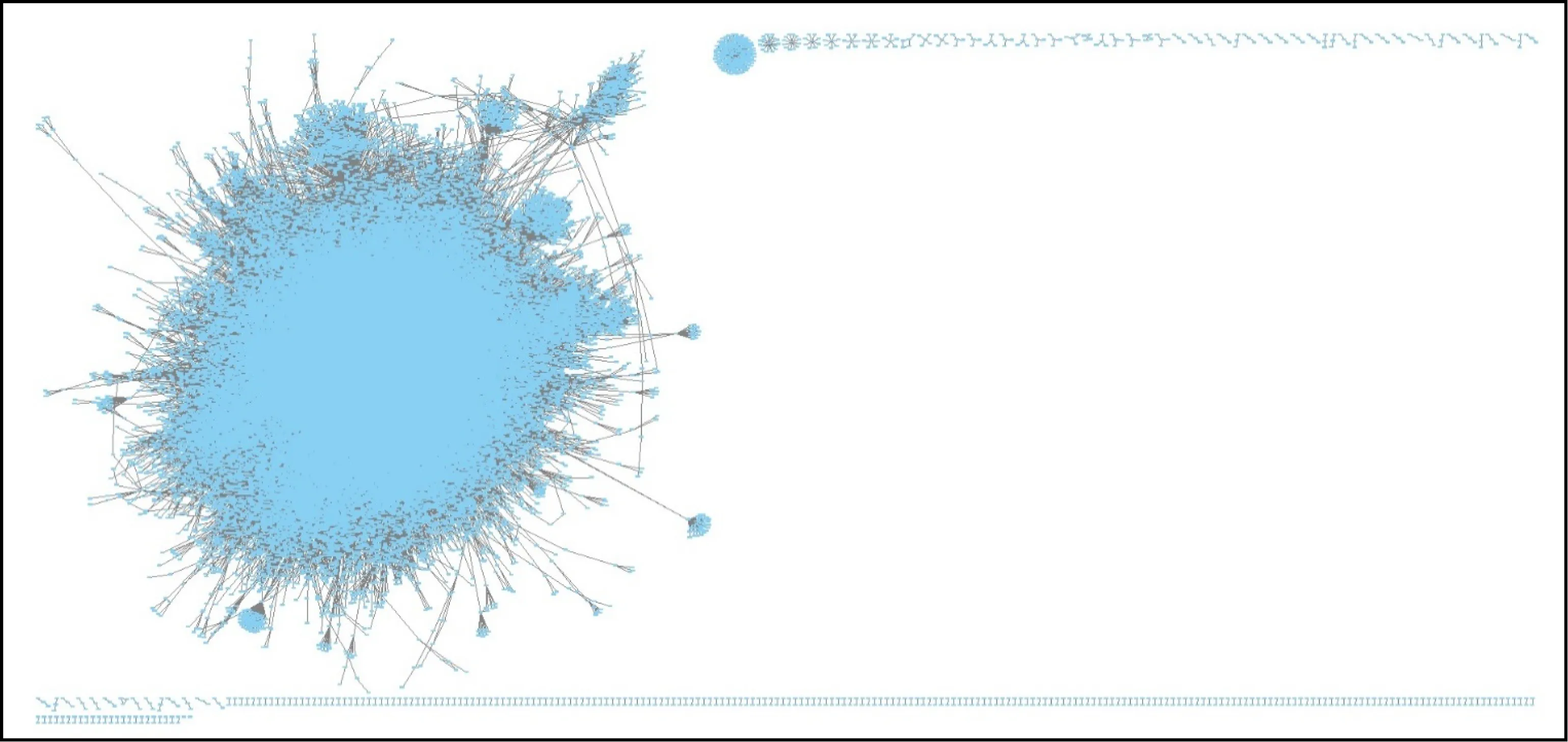
Fig. 3 FCG of c3725-ipbase-mz.124-5
2.1 基本定義
在進行詳細分析和方法描述之前,本節給出基本符號解釋和定義.本文中的圖和網絡、節點和頂點、邊和連邊是等價概念.
定義1.函數調用圖[39].一個由G=(VG,EG)構成的有向圖.其中,VG表示節點集,每個節點對應一個函數,VG={fi|1≤i≤n,i∈},n為函數個數;EG為邊集,表示函數調用關系的全集,EG?VG×VG,EG由序偶組成,若fi,fj∈EG,則存在fi對fj的函數調用.
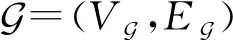
定義3.度.網絡中與當前節點直接相連的邊的數目稱為該點的度,一般使用k表示.對于有向網絡,一個節點指向其他節點的邊的數量稱為出度,記為kout;一個節點被其他節點指向的邊的數目稱為入度,記為kin.
對于一個網絡,式(1)刻畫了網絡的度分布情況:
P(k)=n(k)/N,
(1)
其中,n(k)表示度為k的節點數量,N為網絡節點數量.度數的平均值稱為平均度:
k=2M/N,
(2)
其中,M為邊數量.
定義4.k殼[40].對于一個圖,如果圖中已不存在度數小于k的節點,那么,只要反復剔除度數為k的節點及其連邊,直至圖中不存在度數為k的節點,剩余的圖即為k核,而被剔除的節點和連邊即為k殼.
定義5.余平均度.若節點fi的ki個鄰居的度分別為ki,j,j=1,2,…,ki,則節點fi的鄰居節點的平均度為knni,公式為
(3)
其中,i為節點在圖內的索引值.
所有度為k的節點的鄰居節點的平均度即為k的余平均度,記為knn(k).
定義6.模塊度[37].又稱模塊化度量值,是一種衡量社團劃分質量的標準,對于加權有向圖,其公式為
(4)
其中,W是網絡內所有邊權重和,c表示社團的索引值,nc表示社團個數,Wc表示第c個社團權重和,Sc為所有與第c個社團內節點相關聯的邊的權重和.
定義7.密度.網絡的密度定義為網絡中實際存在的邊數M與最大可能邊數之比.
定義8.聚類系數.網絡的聚類系數有2種計算方法,本文取其中的社會學定義.其公式為
(5)
其中,N表示節點數量,aij表示節點i和節點j是否為鄰居,若為鄰居,則aij=1,反之,aij=0.
定義9.同配系數.同配系數反映了節點與其鄰居節點的度相關性,其公式為
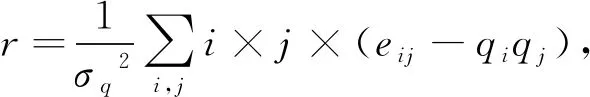
(6)
(7)
其中,eij表示度為i和度為j的節點的連邊數占總邊數的比例.qk表示余度分布,即隨機取節點并隨機取該節點的一個鄰居節點度為k的概率.r為正表示同配,即度大的點鄰居一般是度大的點,反之,r為負表示異配.
定義10.直徑.網絡中任意2個節點之間的距離的最大值為網絡的直徑.
定義11.ER隨機圖.對于N個節點,隨機取M對節點連邊,構成的圖稱為ER隨機圖.
2.2 固件函數調用圖性質分析
由于大規模復雜網絡并沒有定量的衡量標準,只有一些定性的特征.因此,本節將從3個方面分析固件的FCG是否具備復雜網絡的特征.
本節選擇了Cisco IOS的3個系列1 382個固件進行實驗分析(數據集T1,詳見5.2節).這是實際研究過程中所遇到的函數規模最大的一類固件,且不開源,無API,具備分析價值.
2.2.1 稀疏性
文獻[41]指出,大規模網絡的一個共有特征是稀疏性,網絡中邊數遠小于最大可能邊數.文獻[42]指出,也有許多現實網絡中的網絡節點數N與邊數M,介于線性比例關系和平方關系之間,服從超線性關系,稱之為稠密化冪律,如式(8)所示:
M~N?,1
(8)
圖4繪制了固件的節點數及其對應邊數、密度的散點圖,展示了Cisco IOS的3個系列1 382個固件的稀疏性.其中,f(x)是對節點數、邊數對應關系的擬合,斜率5.445,可見固件的邊數與節點數基本服從線性關系.g(x)是對節點數、密度對應關系的擬合,為反比例函數,其密度值隨節點數增大而趨近于0.
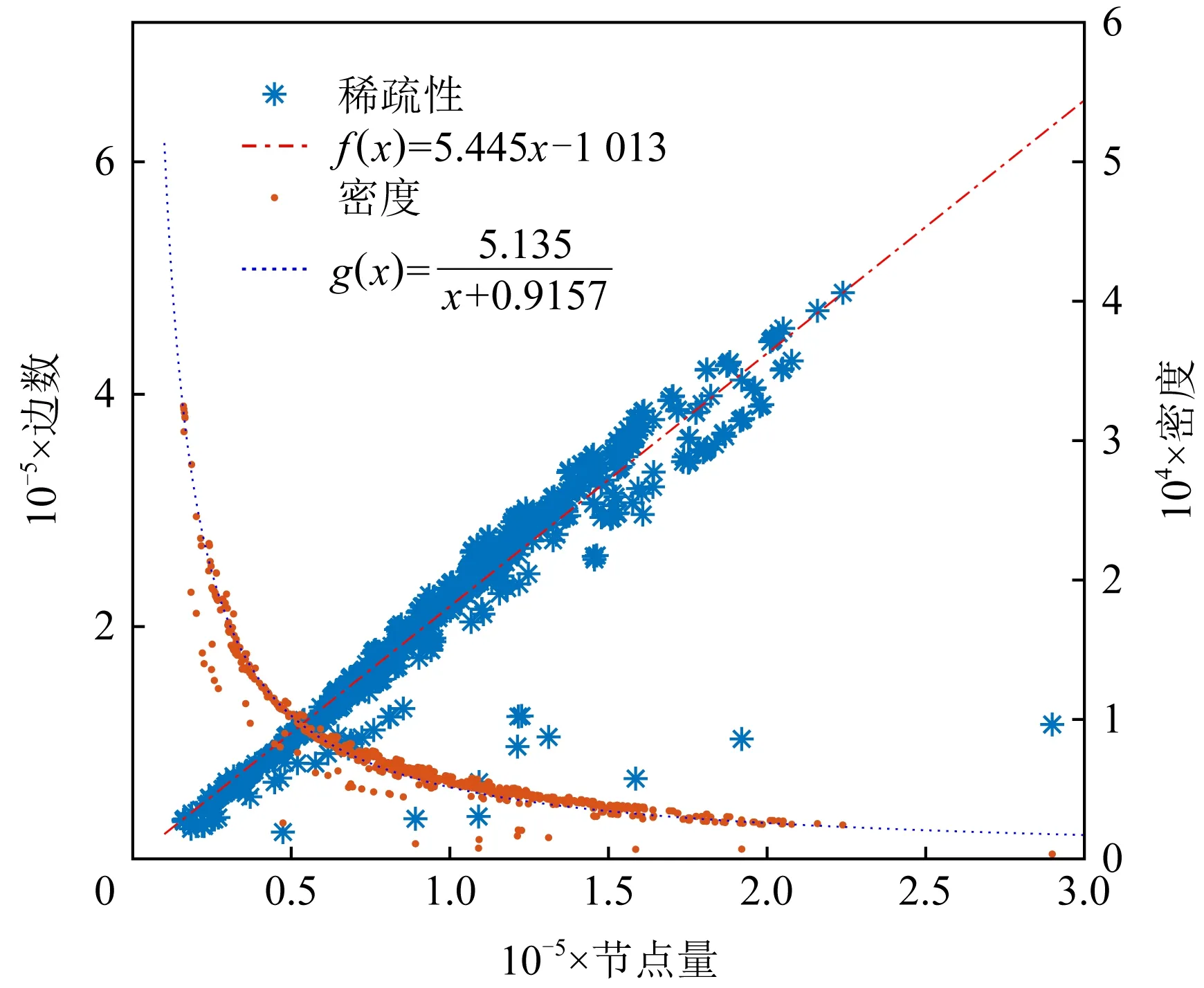
Fig. 4 Firmware sparsity and density
固件的稀疏性服從線性分布可能受軟件開發相關因素影響.開發人員在開發過程中,對于函數間調用和被調用數量存在一個習慣性的分布.若鄰居節點過多會導致程序結構復雜,不利于調試;若鄰居節點過少,則單個函數的規模變大、功能會出現重復.因此,這種分布并未隨著開發對象大小的變化而產生明顯差異.
由此可見,固件的FCG具備一種較為特殊而穩定的稀疏性,具備大規模網絡的特征.
2.2.2 度分布
文獻[43-44]指出現實中的大規模網絡的度分布很多符合冪律分布.而復雜網絡的研究一般是基于這樣的初始條件開展的.文獻[41]指出,現實網絡度分布雖然很多服從冪律分布,但會出現截斷現象,由于度的最大值有限,因此,度很高時冪律分布不成立.
本文根據數據集T1,匯總固件節點信息后,繪制了節點與度數相關的圖例,如圖5所示:
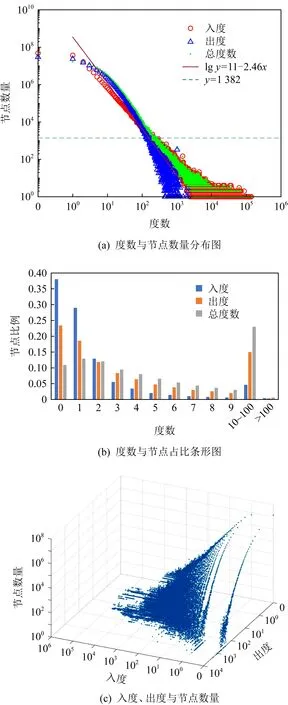
Fig. 5 Firmware degree distribution diagram
圖5(a)反映了節點出度、入度、總度數與節點數量的關系.可以看出,固件中節點度數與節點數量的關系分為2個部分.度數在1 000以下時,近似冪律分布,圖5(a)中擬合了直線,大致可以估計度分布的冪律為2.46;當度數大于1 000時,節點數量基本不再隨度數明顯變化.符合文獻[41]的論述,具備大規模網絡的特征.
需要說明的是,圖5中的節點數量是對1 382個固件的累和,計算單個固件的度分布趨勢應當將節點總數除以固件數量.因此,若圖中節點個數小于1 382,則在單個固件中的節點量可能不足1.
圖5(b)刻畫了節點度數與對應節點數量占比的關系.可以看出,固件中約有10%出入度為0的孤立節點,此類節點將無法直接利用網絡結構進行匹配,只能依靠自身特征結合函數相對固件基址的偏移范圍來進行相似性分析.約有38%的根節點和23%的葉子節點,入度和出度為1的節點也達到了28%和18%,比例較高,這些節點的存在及其規模為網絡壓縮(3.1節)提供了條件.
此外,通過對度分布進行分析,一些基于調用關系傳播的函數匹配問題得以解釋.從圖5(a)(b)中不難發現,由于度數高于100的節點比例不足1%,可知多數函數度數都在100以內.而在度數區間[3,100]內,在數值相等的情況下,入度節點比例低于出度節點比例.說明多數函數連接的子函數數量可能高于父函數數量.由此易知,對于基于調用關系的函數匹配傳播過程,理論上,從根節點向葉節點傳播更易擴展傳播范圍,而從葉節點向根節點的傳播更容易降低待匹配目標函數的篩選難度.
根據固件節點的出入度對應關系與節點數量繪制圖5(c).可以看出,函數節點的入度比出度更容易出現長尾現象.即節點數量較少,但入度極大.此類函數多為庫函數.此現象解釋了為何在固件節點入度普遍低于出度的情況下,實際操作中,向父函數方向進行節點匹配傳播的時間開銷遠大于子函數方向.這或許是文獻[7]研究[7]不采用被調用關系進行傳播匹配的原因.
2.2.3 巨片
文獻[41]指出,現實中的大規模復雜網絡常是不連通的,但存在特別大的連通片,該連通片包含了網絡中相當比例的節點,這種連通片稱之為巨片(giant component).
現有復雜網絡的研究工作多是基于巨片開展的,因為非同一連通片的節點不存在關聯,無法分析其性質.而巨片的節點規模較大,基本可以代表其所處網絡的性質.然而,對于多大規模的連通片可以定義為巨片,既往研究并無相關定義.
本文認為,巨片的規模應當是包括相對性和絕對性2個角度的.相對性是指巨片節點規模在所處網絡達到一定比例,絕對性是指節點數達到一定量級.本文分析的固件節點數量都在萬級以上,只要巨片的節點量達到一定比例,數量上是可以達到絕對性的要求的.
對于巨片規模的相對性.文獻[45-46]指出,當ER隨機圖節點數N→∞,會出現巨片涌現的現象,即,每一個ER隨機圖都會出現巨片;對于ER隨機圖巨片節點占比Pgc與平均度k,給出關系式(9).可以理解為,當節點平均度達到k,會存在巨片且巨片包含的節點比例大于Pgc.
Pgc=1-e.
(9)
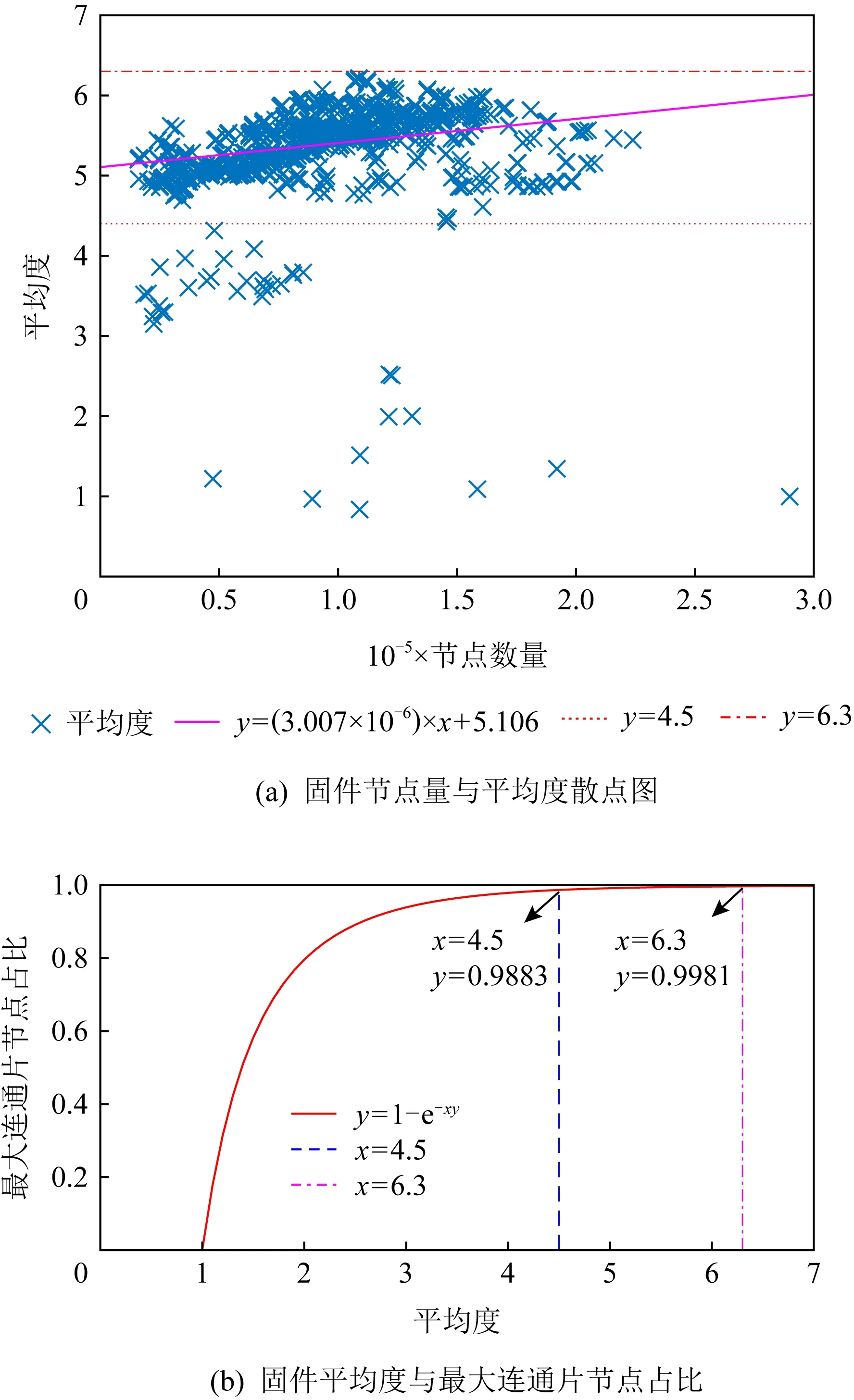
Fig. 6 The oretical derivation of firmware giant component scale
圖6(a)繪制了固件節點數量和平均度的散點圖,可以看出不同規模固件的平均度主要分布在區間[4.5,6.3]內.(分布在區間外的節點有38個,皆為7200系列2003—2006年發布的固件,其原因是該系列這一時期的固件ELF文件中的代碼段和數據段標注為一個段,導致IDA靜態解析錯誤,誤將數據區的數據解析為函數,FCG中因而增加了1~5倍的錯誤節點,以至于平均度被拉低.考慮到后續研究者復現實驗可能會遇到同樣的問題,本文對此現象如實進行描述,以供參考.)
根據式(9)繪制圖6(b),可以看出,若網絡的平均度分布的區間[4.5,6.3],其巨片比例至少可以達到98.83%.
由于式(9)是理論推導,其前提條件是N→∞,而實際條件下N為定值,上述分析可以反映網絡規模不斷擴大帶來的巨片規模變化趨勢,對于有具體值的具體網絡,仍然不夠貼切.
為此,本文繪制了固件節點量和最大連通片占比的散點圖,如圖7所示.從圖7可以看出,固件最大連通片的節點比例相當可觀,普遍在[0.8,0.95]之間,雖然略低于式(9)的推導結果0.98,但與圖5(b)的分析結果相呼應,因為固件中約有1成的節點是孤立節點.由此可知,固件FCG的巨片內密度可能要比預期的高一些.
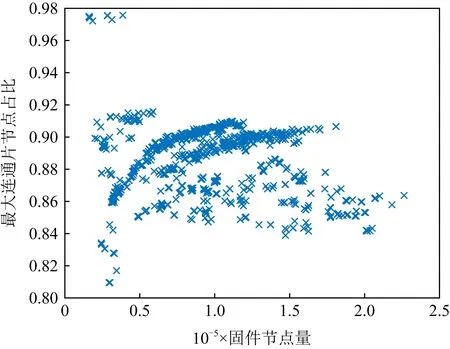
Fig. 7 The proportion of max component node in the firmware
通過上述分析,不難猜想固件的FCG有其特殊性,至少在巨片的規模上,其并不完全符合理論預期.
若要驗證此猜想,首先應當分析與固件FCG同等規模條件下隨機網絡的巨片規模的一般性.為此,本文采用0階零模型和1階零模型[41]進行仿真,通過重復生成符合模型要求且和固件具有相似性的隨機網絡,分析其巨片比例的分布.
其中,0階零模型是指和原網絡具有相同節點數、邊數的隨機網絡,即ER隨機圖;1階零模型指和原網絡具有相同節點數、度分布的隨機網絡.
通過將T1數據集中的固件按2種模型要求,各生成了100個隨機網絡(即進行100次仿真),繪制節點數、最大連通片比例關系圖的散點圖,如圖8所示:
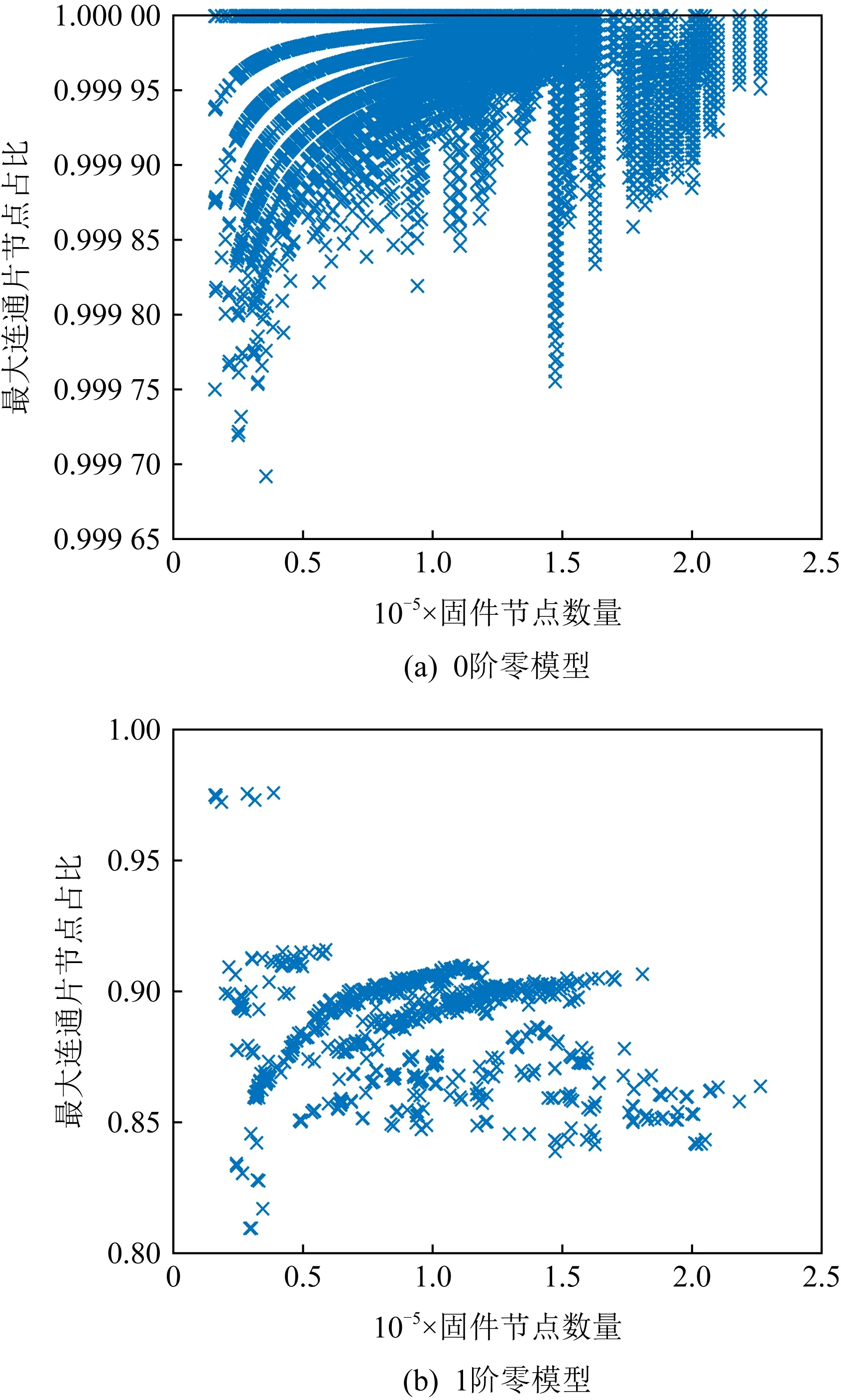
Fig. 8 The proportion of max component node in the simulation network of each 0-order and 1st-order null models
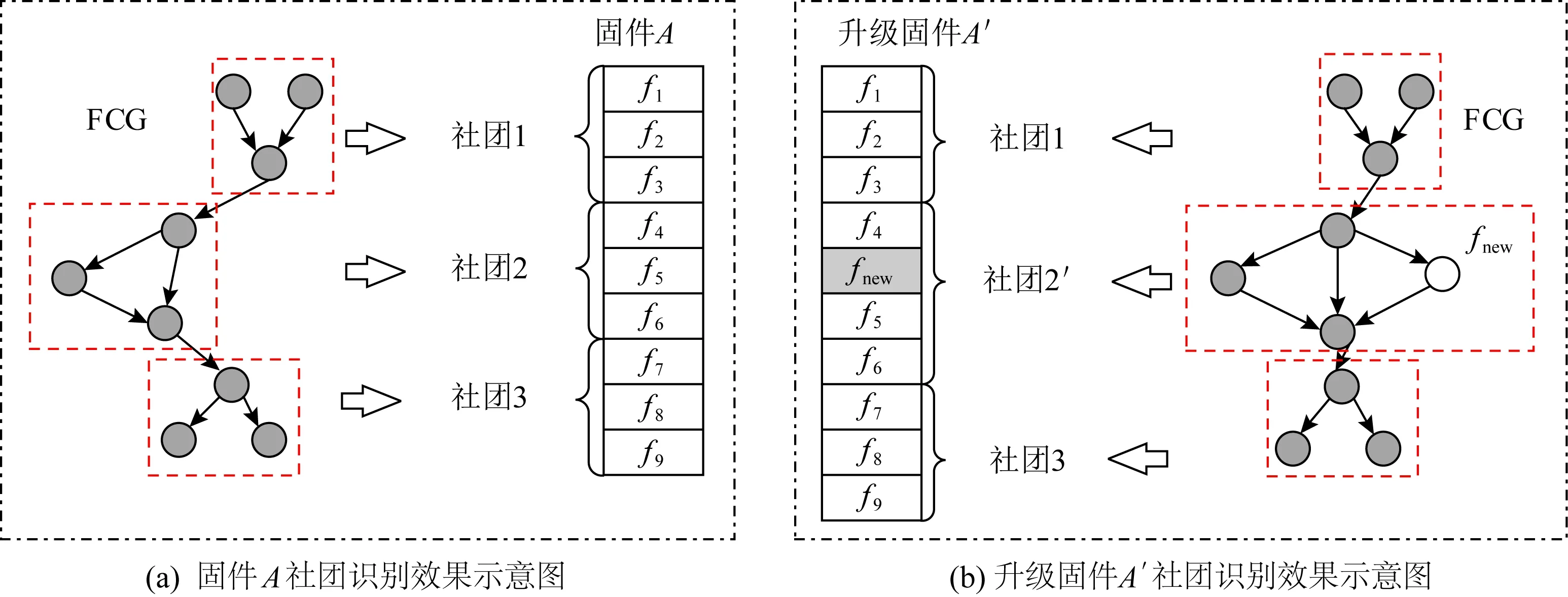
Fig. 9 Comparison diagram of firmware community
圖8(a)是0階零模型仿真結果,可以看出,最大聯通片的節點比例在0.99以上,證明本文選擇的固件,其平均度與巨片規模的關系符合式(9)的理論推導.而固件最大連通片實際節點比例與理論值產生差異的原因可以通過圖8(b)的1階零模型仿真看出,圖8中的最大連通片節點比例與實際固件幾乎一致,說明差異的原因是固件的度分布.如果固件FCG中除了孤立節點,存在一定規模的非最大連通片,那么通過1階模型的重復仿真,一定會產生比例更大的最大連通片.但1階模型多次仿真都沒有產生明顯更高或更低的最大連通片節點比例,說明了2點.一是固件FCG巨片的密度高于達到當前巨片比例的標準;二是固件FCG中不存在成規模的非最大連通片.這驗證了前述猜想,即固件巨片節點比例達不到理論預期是因為固件中大量的孤立節點.
由此,可得出結論,數據集T1的固件FCG一般存在巨片,其巨片規模會受度分布的影響,但服從一定規律.此類固件的規律是,如果固件FCG中的節點不是孤立節點,那么基本會屬于最大連通片,且構成巨片.
3 固件社團檢測與匹配
固件社團檢測的目的是,通過社團檢測,將固件的FCG切割為若干有利于固件比對的子圖.只要找到待比較固件間社團的對應關系,就可以縮小函數匹配過程中目標函數搜索的范圍,其示意如圖9所示.
其邏輯是,程序中往往包含若干功能模塊,功能模塊內的函數間應該具備比功能模塊間函數更緊密的關系.例如:Linux協議棧里可以包括TCP和UDP這2個功能模塊,TCP功能模塊內的函數基本不會與UDP模塊內的函數發生調用關系,但TCP模塊內函數則存在較為密切的關系.理想狀態下,固件社團檢測算法檢測到的社團應當是這樣的功能模塊.
本文設計的固件社團檢測與匹配流程包括3個部分:
1) 固件FCG壓縮.主要對FCG中節點進行合并,減少后續圖分析的工作量.
2) 社團檢測.利用BGLL算法對固件FCG中的社團進行檢測.
3) 社團匹配.選擇社團的統計特征,形成特征向量以刻畫社團,依據特征向量進行社團相似性分析.
3.1 面向社團檢測的函數調用圖壓縮
由于本文的應用場景主要是針對規模較大的固件,因此,對函數調用圖的規模進行壓縮十分必要.通過壓縮,減少函數節點的數量,以減少后續分析的工作量.2.2節對圖5(b)的分析中已經說明,現有固件具備網絡壓縮的條件.
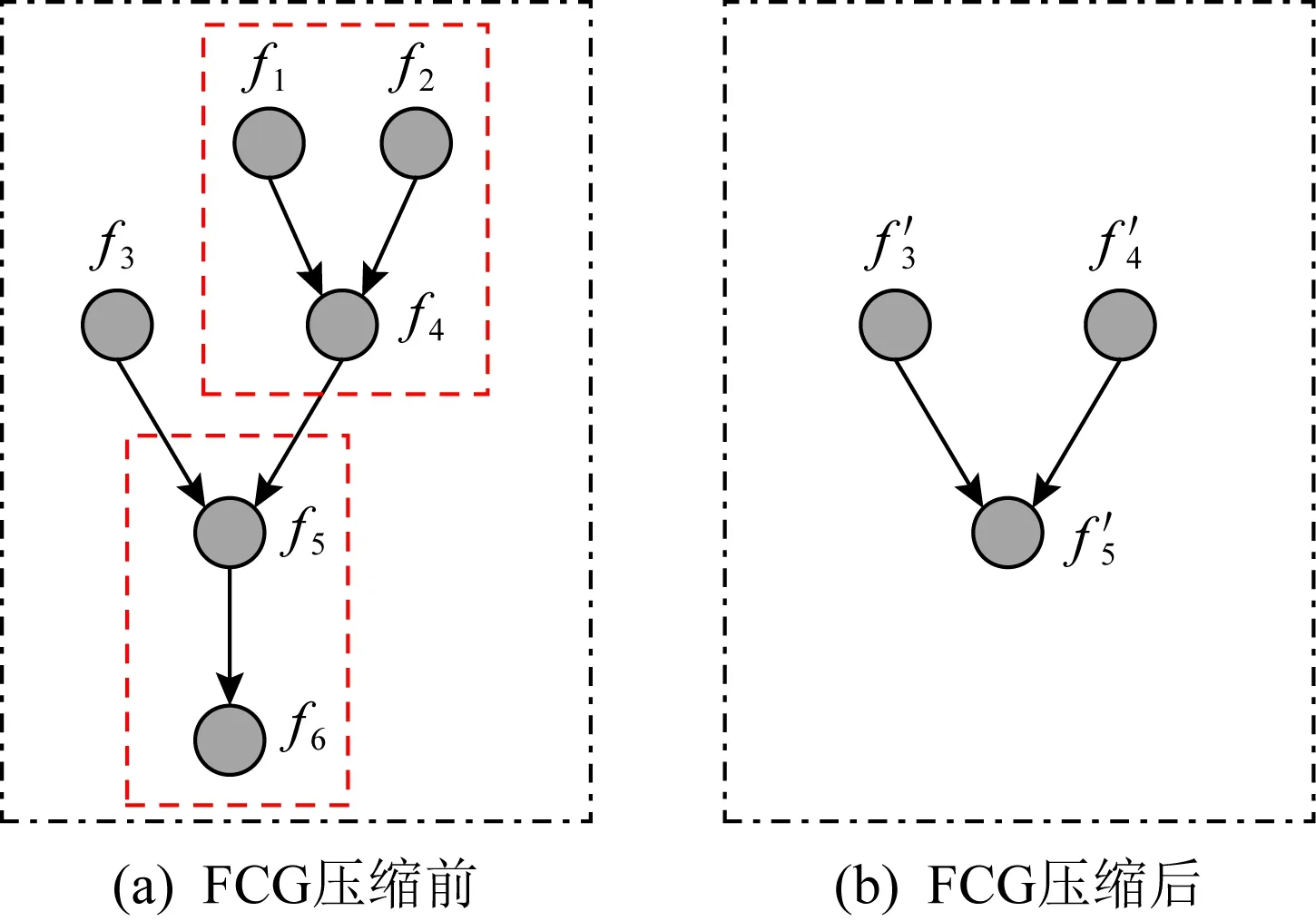
Fig. 10 FCG compression
算法1.函數調用圖壓縮算法.
輸入:函數調用圖G;
輸出:函數壓縮調用圖G′.
① foreach_nodeinVG
② ifeach_node.in_dgree==1且
each_node.out_degree>0
③Add_Node_To_Parent(each_node);
/*將當前節點融入父節點*/
④ continue;
⑤ else ifin_dgree==0且out_degree==1
⑥add_flag=true;
⑦ foreach_parentinget_son(each_node)
⑧ ifeach_parent.in_degree≠0或
each_parent.out_degree≠1
⑨add_flag=false;
⑩ break;
/*將當前節點融入子節點*/
算法1的時間復雜度與FCG的度分布和余平均度有關,包括2種情況:
1) 對于子節點融入父節點的情況,其時間復雜度為O(P(kin=1)×n),n為函數數量,P(kin=1)表示節點入度為1的概率.
2) 對于父節點融入子節點的情況,其時間復雜度為O(P(K)×n×knn(K)),其中K表示事件kout=1,kin=0.
算法1僅表示對圖進行1次遍歷的情況.由于壓縮后,圖的結構會發生改變,部分節點的度值會由于鄰居的融入而發生變化,可能會出現新的符合壓縮條件的情況.因此,可以選擇迭代壓縮.
是否進行迭代壓縮應當具體情況具體分析,其關鍵是不能對后續的社團檢測造成過大影響,即,壓縮前后社團檢測結果出現較大變化.仍以圖10為例,如果迭代壓縮,最后將僅剩余一個節點,會對社團檢測造成干擾.
本文在操作過程中選擇了迭代壓縮的策略,但這是基于實際分析的,實驗表明,本文的實驗對象壓縮前后對社團檢測的影響不大(詳見5.4.3節).
此外,對于壓縮判定條件,即出入度值的選擇問題.邏輯上,是可以選擇度數大于1的節點進行壓縮的.但本文選擇前述條件有3個原因:
1) 度數為1的葉子節點和根節點在社團檢測過程中會歸入其鄰居節點的社團,詳見式(10)~(12).因此,此類節點壓縮不會對社團檢測產生干擾.
2) 選擇入度為1的節點進行合并,而不僅僅選擇入度為1的葉子節點,主要是為了對抗固件升級過程中的函數再封裝現象.即,一個調用關系中插入了新的節點,且新節點僅與原調用關系的2個節點存在調用/被調用關系,與其他節點不存在此關系.
3) 入度為1的節點,表示該函數僅為其父函數提供服務,基本排除庫函數的可能.因此,對其進行壓縮符合函數之間的功能關聯性.
3.2 社團檢測
本文選擇BGLL算法[37]用以對FCG進行社團檢測.BGLL算法處理的對象是連通圖,而FCG一般是非連通圖,故不能對整個FCG直接進行社團檢測.鑒于第2節分析得到的固件FCG性質,固件FCG內的最大連通片多是巨片(如圖7所示),節點若非孤立節點則基本屬于巨片.本文選擇FCG的最大連通片作為社團檢測的分析對象.其算法分為2個階段.
階段1流程為:
1) 初始化目標網絡,假設所有節點為獨立社團.
2) 對于任意相鄰節點fi和fj,計算將節點fi加入fj所在社團是對應的模塊度增量ΔQ.
3) 計算節點fi與所有鄰居節點的模塊度增量,并選擇最大項ΔQi,max.
4) 若ΔQi,max>0,將fi并入其鄰居節點所屬社團,否則保持不變.
5) 重復執行2)~4)步,直到無法合并節點.
階段2需要根據階段1的結果構造新網絡,該網絡的節點為階段1檢測出的社團,節點連邊權重為社團連邊權重和.而后利用階段1的方法對新網絡再次進行社團檢測.重復階段1的5個步驟,直至無法檢測出新的社團.
模塊度增量ΔQ,公式為:
ΔQ=Qnew-Qold,
(10)
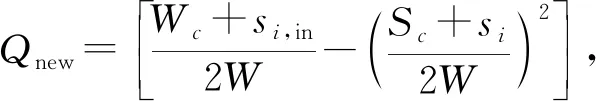
(11)
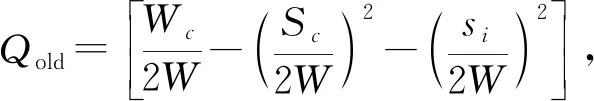
(12)
其中,c為目標社團的索引值,si表示節點fi的強度,即節點fi的連邊權重和.si,in表示節點i的入邊權重和.
BGLL算法適用于固件FCG分析的場景.首先,BGLL算法的處理對象是有向加權圖,用此法分析FCG丟失信息相對少.其次,BGLL的過程是迭代的.單次社團劃分一定程度上割裂了社團間的關聯,而BGLL通過迭代可以得到節點的多重社團歸屬,使得節點可以關聯到比單次劃分更多的節點,有利于后續節點匹配工作的開展.
由于BGLL算法是迭代處理,在指定迭代次數為c的條件下,其時間復雜度應當為O(2×c×m),其中,m是邊的數量.由此可見,其時間復雜度與節點數量無直接關聯.
對于社團檢測的效果,5.4.2節實驗表明,BGLL算法可以將固件75%的節點進行歸類,找到所屬社團.
3.3 社團匹配
社團匹配的目的是找到固件間社團的對應關系,以對后續函數匹配提供支撐.由于社團涉及的節點數量較多,應當盡可能保證匹配準確,避免誤匹配.而對于過小的社團,由于其特征易受節點規模變化影響等多種原因,不進行社團匹配(本文中認定節點個數小于10的社團為小社團,分析見5.4.2節).
本節主要闡述3個問題,社團表示方法、社團差異度量方法和目標社團過濾方法.
3.3.1 社團表示方法
社團是FCG的子圖,因此從圖的角度選擇特征對社團加以刻畫有其合理性.因此,社團表示方法的本質就是子圖的表示方法.
本文選擇了6個特征:
1) 社團節點數,反映社團的規模.
2) 社團密度,反映社團內邊的稀疏性.
3) 聚類系數,反映社團內節點的緊湊程度.
4) 同配系數,反映社團內節點的余度分布趨勢.
5) 直徑,反映拓撲結構.
6) PageRank[47]值累和,反映整個社團內節點在FCG中的重要性.
上述6個特征中,前5個依據定義即可理解.現對第6點加以說明.
PageRank值累和,就是利用PageRank算法求得各個節點在FCG中的值,而后將一個社團內的所有節點的PageRank值求和,以表示該社團的重要性.
PageRank是一種衡量網頁重要性的算法.由于該算法原始版本存在懸掛點的問題.本文使用的是一種修改后的PageRank算法,其流程為:
1) 初始化,對節點數為N的FCG中各個節點進行PageRank值(記為PR值)賦值,賦值為1/N.
2) 第h輪的PR值依據第h-1輪的PR值求得.每個節點的PR值,在下一輪運算中,首先通過比例因子α進行縮減,縮減的部分均分給所有節點;再根據出邊的權重占當前節點出邊權重和的比例,將未縮減部分分配給各子節點.對于節點i,PR值為
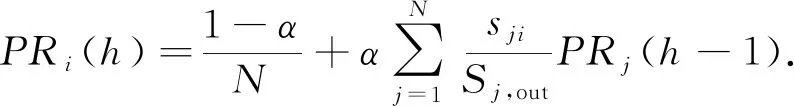
(13)
由于縮減比例α需要根據實際情況調整,并無定值,早期研究推薦α=0.85,本文在5.4.4節中對于適用于固件分析的α值進行了實驗.依據實驗結果,選擇α=0.9作為后續分析的指定參數.
PageRank值累和對于社團表示十分重要,是上述6個特征中唯一可以反映社團外節點信息的特征,其信息來源可以涵蓋到根節點.若一個固件內檢測出同構的社團,則只能根據各社團在整個網絡的價值差異加以區分.如Cisco IOS中TFTP,ICMP等功能模塊常有獨立的內存處理模塊(memset_s,memcpy_s等函數),這些內存模塊基本都是同構的(其原因可能是靜態鏈接或者拷貝代碼).此時,對內存模塊的區分可以依靠PR值.
3.3.2 社團差異度量
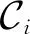
Diff(Ci,Cj)=(μ1,μ2,…,μ6),
(14)
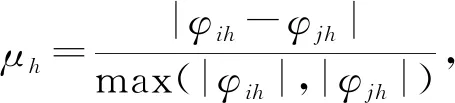
(15)
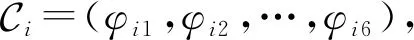
(16)
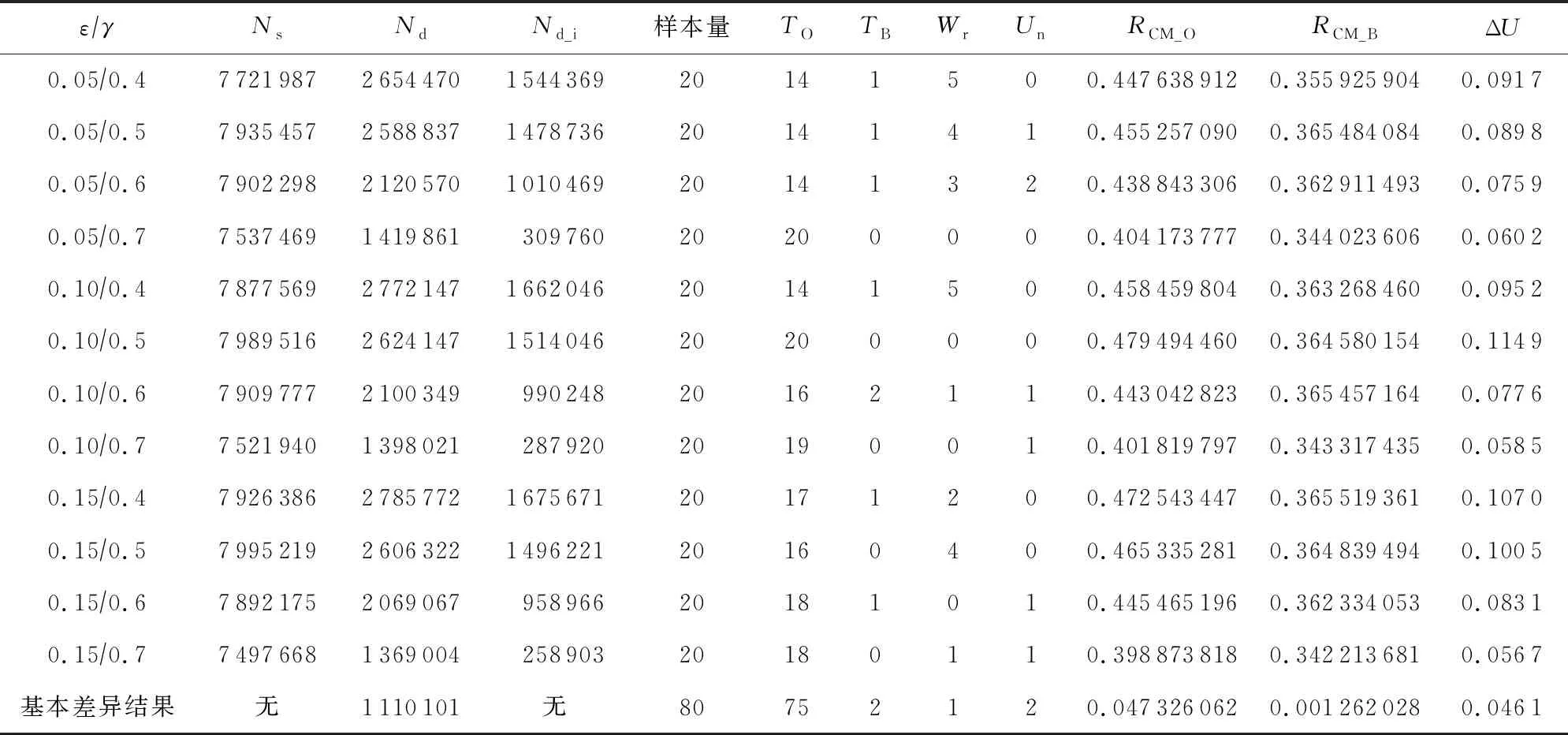
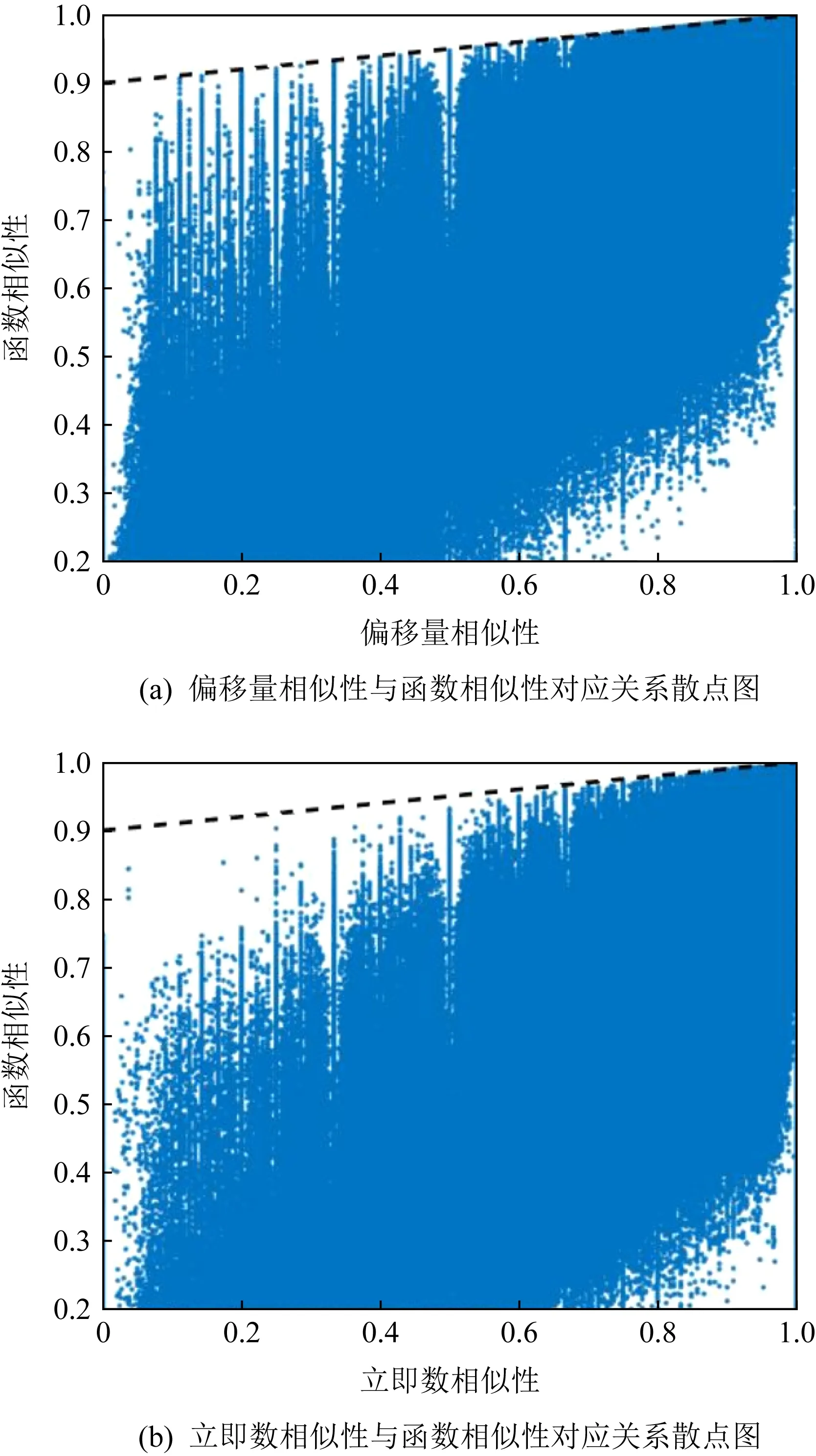
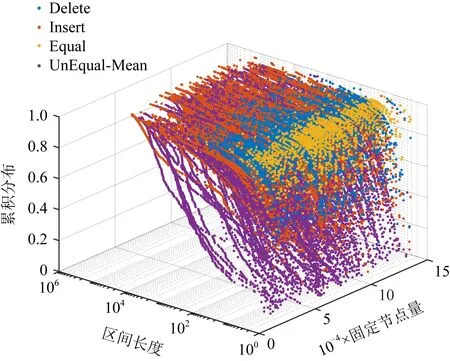
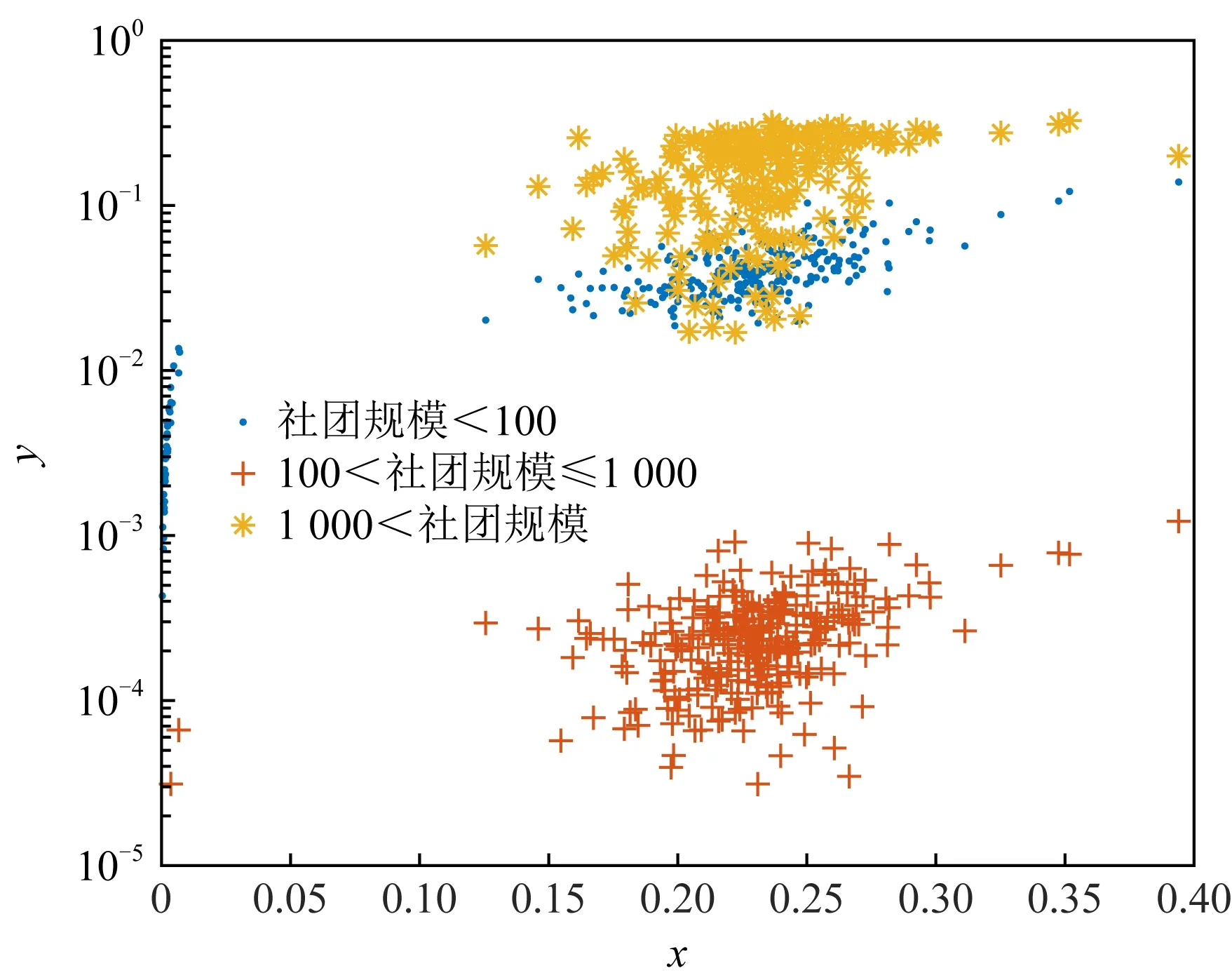
其中,φih表示社團Ci的第h個特征,h∈,0 3.3.3 目標社團過濾 目標社團過濾的目的是根據社團差異度確定社團的匹配關系. 由于不同的固件會存在函數數量和調用關系的不同,因此,即使具有對應關系的函數,其所屬社團也常會存有一定差異性.而社團匹配結果影響到后期節點匹配的結果,應當選擇較為保守的匹配策略.故既要允許匹配社團有一定差異性,又要避免誤匹配,本文使用的策略為: 對于待比較固件A,B,現有社團Ci∈A,Cj∈B,若其差異度Diff(Ci,Cj)滿足μi,j,h<β,h∈,0 在實際操作過程中,若固件本身相似性較低(如待比較固件的函數規模差異較大),可以適當放寬PR值特征的差異度衡量閾值,或者依據PR值大小排序后的索引值進行差異度衡量. 在5.4.7節,本文將對β的選值進行實驗分析,實驗表明β=0.35較為理想. 根據第3節的方法可以獲取固件中部分社團的對應關系,但并未進行函數匹配.本節將闡釋基于匹配社團的函數匹配方法. 首先,本節將介紹函數相似性度量方法,說明新引入的特征. 而后,闡釋利用匹配社團引導函數匹配的方法.其流程包括:匹配社團的函數匹配、誤匹配函數修正、殘余函數匹配3部分.其中,匹配社團的函數匹配主要尋找匹配社團內的匹配函數;誤匹配函數修正主要針對匹配社團的誤匹配節點進行修正;殘余函數匹配主要針對無社團節點、非匹配社團節點、匹配社團未匹配節點3類進行匹配處理. 對于函數fi和fj,本文計算其相似性: (17) 其中,Popc表示函數操作碼相似性,Popn表示操作數相似性,Pcall表示調用關系相似性.w1,w2,w3是其權重,本文選擇的權重為300,80,100. 權重選擇的一個主要考量是,如果特征在不同版本的固件中具有穩定性,則權重應當相對高;反之,如果特征易受版本變化影響,應當適當降低其權重. 對于權重的具體參數,本文不再進行實驗分析.一則本文的重點不在于單點函數相似性的計算方法而在于對新特征的選擇;二則對于函數相似性度量的權重選擇工作,前人已經有過研究,方法上并無改進,且當前參數的實驗效果已經較為理想. 4.1.1 操作碼相似性 對于函數操作碼相似性,本文選擇最長公共子序列(longest common subsequence, LCS)算法進行度量,而后計算LCS長度與最大函數長度的比值,作為操作碼相似性.其公式為 (18) 4.1.2 操作數相似性 操作數相似性包括2部分,偏移量相似性Poff和立即數相似性PImmi.其計算公式為 Popn=max(Poff,PImmi). (19) 實際操作中,也可以使用算術平均或加權平均的思路,如式(20): (20) 本文較為推薦式(19),其原因在于,操作數值隨固件版本變化而變化的情況相對常見.因此,若出現操作數相似度較高的情況,則函數可能較為相似.此時,若用加權平均的思想處理操作數相似性問題,將可能降低此特征的價值. 此外,如果分析了偏移量相似性和立即數相似性所反饋的現實意義,就可以理解,加權平均的思路是對函數同時在2個方面的相似性存在要求,這是一種較為苛刻的構想. 實際運算中,函數相似性Sim(fi,fj)的值也會因為Popn值較低而受到影響,在進行匹配函數篩選時需要避免賦予過高的權重(詳見5.4.10節). 4.1.2.1 偏移量相似性 此處偏移量是指匯編指令中相對于寄存器的偏移值.以PowerPC語句為例,lbz r9,0x8F(r3)中,0x8F就是相對于寄存器值的偏移量. 偏移量反映了結構體信息.對于固件比較而言,在不同版本的固件中,匹配函數的結構體應當是保持穩定的.結構體中成員的偏移量應當是固定的,即使有成員增刪,偏移量也應當是整體性的增大或減小,如圖11所示: Fig. 11 Examples of structure changes 因此,對于函數fi的偏移量集合Soff(fi),函數fj的偏移量集合Soff(fj),偏移量相似性Poff的計算流程為: 1) 計算偏移量的均值Eoff(fi),Eoff(fj). (21) yh=xh-Eoff(fi),xh∈Soff(fi). (22) 3) 利用Jaccard指標J計算集合相似性,并按式(23)求得Poff. (23) (24) (25) 4.1.2.2 立即數相似性 立即數在函數中會反映一些特定信息.如:Cisco IOS中用0xDEAD表示異常,HTTP協議處理模塊中立即數8080表示端口,指令解析器中使用字母的ASCII碼表示指令的首字母縮略. 對于函數fi的立即數集合SImmi(fi),函數fj的立即數集合SImmi(fj),本文使用Jaccard指標J計算立即數相似性PImmi: PImmi=J(SImmi(fi),SImmi(fj)). (26) 4.1.3 調用關系相似性 對于一個存在m個父函數的函數fi,根據函數起始地址在固件中的先后順序可以由小到大獲得父函數的索引值,根據函數索引排序父函數,計算臨近父函數之間的索引距離spi,可以構建具有m-1個元素的集合SPindex(fi)={sp1,sp2,…,spm-1},用以表示函數. 因此計算fi和fj父函數相似性: Pparent=J(SPindex(fi),SPindex(fj)). (27) 同理,可以計算出子函數相似性Pson.調用關系Pcall,由兩者計算算術平均得出. 3.3.3節提到匹配社團之間允許差異存在.匹配社團并不代表社團同構,也不意味著社團節點數量相同.因此,并非社團內所有函數都存在匹配對象,在進行匹配社團間的函數相似性計算后,應當篩選匹配函數對.此外,雖然進行了社團劃分,但依然存在一定比例的社團,其節點數量較大,甚至達到上萬個節點(見5.4.2節).有鑒于此,匹配社團的函數匹配工作需要從候選函數過濾和匹配函數篩選2方面開展. 候選函數過濾的目的是在每個社團中找到1組候選函數節點用于比較,以降低匹配函數的篩選范圍.匹配函數篩選則是要對2組候選函數節點進行相似性分析,并挑選出匹配函數. 對于匹配社團Ci和Cj,其函數匹配算法如算法2所示. 算法2.匹配社團函數匹配算法. 輸入:匹配社團Ci和Cj; 輸出:匹配節點集合Matched_Node. ①Max_k,I_ksdic,J_ksdic=Get_Kshell(Ci, Cj);/*對社團進行k殼剝離,完成初始 過濾,并提取k殼最大值*/ ② for (h=Max_k;h>0;h--) ③m_nodes=MatchGP(I_ksdic[h], J_ksdic[h]);/*從候選函數中挑選 匹配節點*/ ④Matched_Node.append(m_nodes); ⑤ end for ⑥Neighbors=Get_Neighbor(Matched_Node); /*根據鄰居節點進行候選函數過濾*/ ⑦ whileNeighbors≠None ⑧m_nodes=MatchGP(Neighbors); /*從候選函數中挑選匹配節點*/ ⑨Matched_Node.append(m_nodes); ⑩Neighbors=Get_Neighbor(Matched_Node); 候選函數過濾,首先根據k殼值對2個匹配社團的節點進行劃分,取k殼值相等的節點構建2個候選函數組,并對2組間的函數逐對分析相似性(5.4.5節對社團的k殼值分布進行分析). 在確定部分匹配節點后,候選函數過濾將基于調用關系,選擇匹配函數的鄰居節點構建候選函數組,并對2組間的函數逐對分析相似性. 匹配函數篩選是在已經計算過候選函數組間節點相似性的情況下進行的.對于函數組F1,F2,若函數fi∈F1,fj∈F2和其他函數fi′∈F1,fj′∈F2,fi≠fi′,fj′≠fj,滿足3個條件,則認為函數fi與fj匹配. Sim(fi,fj)>γ, (28) Sim(fi,fj)-Sim(fi,fj′)>ε, (29) Sim(fi,fj)-Sim(fi′,fj)>ε. (30) 對于閾值γ和ε,本文將進行實驗并于5.4.8節和5.4.9節討論,取γ=0.5和ε=0.1是效果最好的值. 此外,由于本文采用的是BGLL算法,在完成低層次社團的節點匹配工作后,可以利用節點所屬的高層次社團,在更大范圍內挑選候選函數組進行函數匹配. 程序在編譯過程中,如無特殊需求,服務于相同功能模塊的函數往往存放在較為接近的內存區間.因此,如果社團內包含同一功能模塊的函數,社團內函數地址應當較為接近.通過5.4.6節的實驗可以發現,社團內節點確實分布在相近的地址區間. 基于4.3節所述構想和實驗結果,本文提出了基于地址分布的誤匹配函數修正方法,用以修正匹配社團函數匹配階段的誤匹配問題. 定義12.未匹配區間.對于固件A,B,有函數fi∈A,fj∈A,i 誤匹配函數修正流程為: 1) 提取固件中的未匹配函數區間. 2) 誤匹配函數修正.對于1對未匹配區間(i,j)和(i′,j′),若j-i<τ且j′-i′<0,則將未匹配區間邊界的匹配函數重置為未匹配狀態. 3) 反復執行上述2個操作,直到匹配函數數量不再變化. 對于2個待比較固件,如果發生誤匹配,有函數匹配了對應功能模塊外內的函數,那么該函數與其相鄰函數會形成未匹配區間,如流程2中所示. 當然,固件中也會有功能模塊因為升級而出現整體性位置遷移的情況.此時功能模塊的邊界會產生和誤匹配相近的情況,如圖12所示.其中,由于fi與節點fh的誤匹配,形成了1對未匹配區間(i,i+1)和(h,i′+1)且h>i′+1.而對于社團整體性遷移,同樣帶來了1對未匹配區間(j+1,l-1)和(j′+1,l′-1)且j′>l′,兩者成因不同而情況相似. Fig. 12 Examples of matching false positives 因此,誤匹配修正使用τ對修正范圍進行限制,避免把發生整體性位置遷移的功能模塊的匹配函數全部重置.另外,誤匹配修正工作僅在匹配社團的節點匹配工作之后進行,不在其他階段開展,避免出現因修正帶來匹配-重置的死循環. 本文中τ=10,對選值的大小不再進行比較分析.τ=10的合理性在于,若1個匹配社團存在跨度大于10的相鄰匹配函數,而另一社團對應的匹配函數之間相距較遠甚至發生錯位,一般說明2個函數不屬于同一功能模塊.對于修正后的未匹配區間大小,于5.4.11節進行實驗分析. 經過誤匹配修正的固件仍然存在一定量未匹配函數,主要包括:匹配社團的未匹配節點、未匹配社團以及無社團節點.此時,固件被劃分為若干個未匹配區間,若未匹配區間的大小較為合理,可以直接利用未匹配區域構造候選函數組完成剩余的匹配工作,對于殘余函數節點的類型不再區分處理. 對于固件A,B,其殘余函數匹配算法如算法3所示. 算法3.殘余函數匹配算法. 輸入:固件A,B; 輸出:匹配節點集合Matched_Node. ①Add_Matched_Num=-1; ② whileAdd_Matched_Num≠0 ③U_Region=Get_U_Region(A,B); /*獲取未匹配區間*/ ④N_match1=MatchGP(U_Region); /*基于候選函數組統計特征篩選*/ ⑤U_Region=Get_U_Region(A,B); /*獲取未匹配區間*/ ⑥N_match2=Match_contin(U_Region); /*基于地址連續篩選*/ ⑦Matched_Node.append(N_match1, N_match2); ⑧Add_Matched_Num=max(len(N_ match1),len(N_match1)); ⑨ end while 候選函數組統計特征篩選采用和匹配社團節點匹配方法中相同的篩選策略,條件如式(28)~(30). 基于地址連續的篩選策略每次僅比較與匹配節點相鄰的未匹配函數.具體而言,對于1對未匹配區間(i,j)和(i′,j′),若函數fi+1,fi′+1未匹配,且滿足式(31),則認為兩者匹配.fj-1,fj′-1判定匹配的條件一致. (31) 本節將對第3節和第4節提及的若干問題進行實驗并說明,實驗包括12個:函數調用圖壓縮效果、社團檢測效果、FCG壓縮對社團檢測的影響、社團規模與PageRank值關系及參數選擇、社團內節點的k殼值分布、社團內節點地址分布的局部性、社團匹配的參數選擇、函數匹配的參數選擇對匹配效率的影響、函數匹配的參數選擇與Bindiff比較實驗、操作數相似性與函數相似性關系、未匹配區間長度分布、匹配社團對節點匹配的貢獻. 本文實驗環境為Win10 x64操作系統,Intel Xeon W-3175X CPU@3.10 GHz處理器,384 GB內存,Samsung T5 SSD 2TB硬盤.使用軟件IDA pro[48],進行輔助分析.實現語言是Python 3.7 x64. 本文測試主要使用2個數據集: 1) 數據集T1. 1.1節指出了既往研究使用開源軟件編譯數據集存在軟件規模較小的情況,不適用于驗證固件比對技術.因此,基于Cisco C2600(640個)、C1800(301個)、C7200(441個)系列共計1 382個固件,建立此數據集. 2) 數據集T2.從數據集T1每個系列固件中抽取80對固件,構成3組共計240對固件.本數據集用于評估同系列固件的社團匹配和節點匹配效果,共計21 990 414對函數需要進行匹配(每對固件取函數數量較小者進行統計). 進行固件比對分析前,需要對固件進行解析.主要依靠IDA pro進行反匯編,并提取函數比對需要的基本信息.本文對收集的1 382個固件進行了預處理,包括為Bindiff比對提前生成Binexport文件. 5.4.1 函數調用圖壓縮效果 本實驗對數據集T1的所有固件使用3.1節中的函數調用圖壓縮算法進行壓縮后,用壓縮率對壓縮效果進行衡量. 定義13.壓縮率(compression rate).壓縮率PCompression為 PCompression=N′/N, (32) 其中,N′是固件壓縮后的節點數量,N是壓縮前的節點數量. 根據固件節點數量和其進行執行壓縮算法后的壓縮率繪制散點圖如圖13所示.從圖13中可以看出,對于現有樣本,算法1的壓縮率普遍在[0.55,0.7]區間.壓縮算法為后續的社團檢測降低了至少30%的節點規模. Fig. 13 Compression rate of FCG compression algorithm 5.4.2 社團檢測效果 本實驗對數據集T1的所有固件在使用FCG壓縮后,利用BGLL算法進行社團檢測,社團檢測效果如圖14所示. 圖14(a)用散點圖刻畫了各個固件中無社團節點和小社團節點(社團節點量小于10)的占比;橫軸為進行FCG壓縮后的固件節點量,縱軸為節點占固件比例. 圖14(b)用散點圖刻畫了各個固件通過BGLL算法檢測出的社團數量以及各固件內小社團(社團節點量小于10)數量的占比.橫軸為進行FCG壓縮后的固件社團量,縱軸為小社團的數量占比. 圖14(c)用條形圖刻畫了社團節點量在不同范圍的社團,其數量占據所有固件社團的比例.橫軸為社團數量占比,縱軸為節點個數在不同范圍的社團. 圖14(d)用條形圖刻畫了社團尺寸相對其所屬固件在不同比例范圍的社團,其社團數量占據所有固件社團的比例.橫軸為社團數量占比,縱軸為社團內節點量與社團所屬固件節點量的比值. 圖14(e)用散點圖刻畫了固件規模、社團大小、社團數目的關系.x軸為進行固件FCG壓縮后的節點量,y軸為社團內節點量,z軸為相應社團的數量. 圖14(f)用散點圖刻畫了固件規模、社團相對大小、社團數目的關系.x軸為進行固件FCG壓縮后的節點量,y軸為社團內節點量對其所屬固件節點量的比值,z軸為相應社團的數量. Fig. 14 BGLL algorithm community detection effect 通過分析圖14,可以得出3個結論: 1) 社團檢測算法可以為使固件中75%以上的節點找到所屬社團. 從圖14(a)中可以看出,無社團歸屬的節點一般占固件總結點數的15%~25%,由此可知,固件節點的至少75%在二進制比對的函數匹配過程中,可以根據固件社團檢測結果對匹配對象進行過濾.如果考慮到固件普遍有10%左右的孤立節點,也可知最大連通片中無社團歸屬節點的比例不到固件總節點量的15%.此外,鑒于社團規模小于10的社團,其節點量約占固件總結點量的10%~20%.可知,本文雖然排除了小社團(節點量小于10)進行社團匹配的情況,但仍可以保證固件55%以上的節點在二進制比對過程中對匹配對象形成有效過濾. 2) 不對小社團進行社團匹配,降低了工作開銷,但基本保證了節點比對效果. 從圖14(b)中可以看出,節點量小于10的小社團其數量達到固件總社團數的70%以上,不對其進行社團匹配減少了70%的工作量.而根據圖14(a)可知,即使不對小社團進行社團匹配,仍然能保證固件至少55%節點其所屬社團能夠參與到社團匹配過程中. 3) 如果節點所屬社團存在匹配社團,那么在節點匹配過程中,社團檢測算法將該節點的匹配節點搜索范圍減少了近90%. 通過圖14(c)~(f)不難發現,99%以上的社團內節點量小于500、社團規模占其所屬固件節點比例1%以下.說明社團檢測算法檢測出的社團,從減少節點匹配的目標節點搜索空間這一目的而言,具備較好的效果.而社團檢測算法檢測出的社團,其節點量最大不到15 000,占所屬固件節點比例不到12%.由此可知,該社團內節點在完成社團匹配進行匹配節點搜索時,最多僅需搜索固件12%的節點. 此外,通過圖14(e)(f)不難發現,固件中存在一些社團其規模大致隨固件規模增大而增大,比例約為0.095和0.06.這類社團可能是固件的核心功能模塊,用以將固件不同的功能模塊聯系到一起,但通過比例可以看出此類社團占比較少.而其他社團則受固件規模變化影響較小,相對具有穩定性,有利于開展不同規模的固件間的社團匹配工作. 5.4.3 FCG壓縮對社團檢測的影響 本文于3.1節提出了壓縮FCG以降低社團檢測時間開銷的方法.FCG壓縮會改變其拓撲結構,對社團檢測結果會造成影響,因此需要分析FCG壓縮帶來的影響大小. 定義14.壓縮前社團穩定率.對于FCG壓縮前檢測出的社團Ci,其節點量為|Ci|,有FCG壓縮后檢測出的社團Cj,2個社團交集的節點量為|Sc_inter,i,j|,且對于FCG壓縮后檢測的任何社團Ch,Ch≠Cj,有|Sc_inter,i,j|>|Sc_inter,i,h|,則壓縮前社團穩定率PB_S滿足: (33) 同理,易知壓縮后社團穩定率PA_S,不做贅述. 本節設計實驗如下.使用數據集T1,分別在壓縮前和壓縮后進行BGLL社團檢測.繪制壓縮前社團穩定率和壓縮后社團穩定率的累積分布散點圖,如圖15所示.其中,x軸為社團相對大小(社團節點量比固件節點量),y軸為社團穩定率(紅色叉為壓縮前社團穩定率、藍色點為壓縮后社團穩定率),z軸為社團穩定率的累積分布值(小于y軸社團穩定率的社團數量占比). Fig. 15 Cumulative distribution diagram of community stability rate before and after compression 從圖15中可以看出,壓縮前社團穩定率低于50%的社團累積分布約為20%,意味著80%以上的壓縮前社團可以保證50%以上的節點壓縮后仍處于同一社團,而壓縮后的社團可能包含來自多個社團的不同節點. Fig. 16 Relationship between community size and PageRank value 由此可見,FCG壓縮會使社團規模更大,但對壓縮前的社團破壞有限,可以基本保證主體社團結構的穩定. 5.4.4 社團規模與PageRank值關系及參數選擇 本節探討社團規模與PageRank值的關系,主要驗證PageRank值是是否能在社團匹配過程中用于區分社團.基于這樣的目的,對PageRank算法的縮減比例因子α的選擇進行實驗分析,挑選效果最好的比例因子. 本實驗對數據集T1的所有固件在壓縮并利用BGLL算法檢測社團后,使用PageRank算法,根據社團內節點的PageRank值求和得到社團的PageRank值.在α取0.5,0.6,0.7,0.8,0.9的條件下,重復上述實驗.根據實驗結果,繪制圖16和表1. 圖16(a)用散點圖刻畫了社團節點量、社團PageRank值及相應的社團數量,在不同α取值條件下的實驗結果. 圖16(b)用散點圖刻畫了社團相對大小(社團節點量相對固件節點量)、社團PageRank值及相應的社團數量,在不同α取值條件下的實驗結果. 圖16(c)用散點圖刻畫了固件節點量、固件內社團(社團節點量)PageRank值的方差,在不同α取值條件下的實驗結果. 圖16(d)用散點圖刻畫了社團節點量、社團PageRank值的方差及相應的社團數量,在不同α取值條件下的實驗結果. Table 1 Variance of PageRank Value of Communities with Different Node Amounts 表1展示了在不同α取值條件下,數據集T1所有社團的PageRank值方差、節點量大于1 000社團的PageRank值方差和節點量小于1 000社團的PageRank值方差. 根據圖16(a)(b)可以看出,社團PageRank值最大不超過0.15,且社團規模小于1 000時PageRank值波動較大,而大于1 000時,存在一些社團PageRank值隨社團規模增大而成比例的增大.此外,α取值不同對數據集內的PageRank值分布情況并無明顯影響. 通過觀察表1中社團的PageRank方差可以發現,對于所有社團而言,α取值帶來的方差變化較小.對于節點量大于1 000的社團,α取0.5,0.6時PageRank具有較好的區分效果,而對于小于1 000的社團,取值0.7,0.8,0.9具有較好的取值效果. 如果觀察各個固件內的PageRank值波動情況,如圖16(c)(d),則可以發現,在節點量小于1 000的條件下,α=0.9時社團PageRank方差大于其他取值,說明可以更好地區分固件內社團.而在節點量大于1 000的條件下,α=0.9時PageRank方差相對小,區分度相對小. 本文認為,α=0.9是較為合理選擇,基于如下考慮. PageRank值由2部分構成,其中節點PageRank值中有1-α的比例是平均分給固件內各個節點的(隨機分配條件下,各個節點分到的PageRank期望值是相同的),而剩余的α則是依據節點間調用關系確定的. 由此可知,社團PageRank值一部分由社團內節點量構成,一部分依據調用關系構成.對于PageRank值受節點量影響的部分,α取值越小,相應值越大.對于大社團,可以直接通過節點量區分不同社團,無需利用此部分值區分社團;對于小社團,節點少量的波動,就會對此部分產生影響,而小社團節點波動較為常見,此時更應該關注社團內外的調用關系穩定性. 因此,對于大社團,α取值越小PageRank值的價值越小;而對于小社團,α取值越大,對社團區分效果越理想.在這樣的條件下,α=0.9較為合理,實驗結果也能支撐上述觀點. 5.4.5 社團內節點的k殼值分布 4.2節提及,在匹配社團的節點匹配算法中,依據k殼值對社團內節點進行劃分,以減小匹配函數的篩選范圍,特別是針對節點規模較大的社團.使用k殼值對社團內節點進行劃分是否合理需要實驗驗證. 現對數據集T1所有社團內的節點進行k殼值分析,繪制如圖17所示: Fig. 17 Proportion of k-shell value of nodes in the community 圖17(a)是社團內不同k殼值節點占比的累積分布散點圖.x軸表示社團相對規模,即社團節點量與固件節點量的比例;y軸表示社團內相應k殼值節點的占比;z軸為符合條件的社團數量占比的累計分布,條件為,社團內小于等于指定k殼值的節點比例小于對應y軸的值. 圖17(b)是社團相對規模與指定k殼值節點占比的散點圖,每一個點對應一個社團的指定k殼值節點占比. 從圖17可以看出,當k>4時,k殼值的增加不會帶來社團內節點比例的明顯變化,因此,在選擇k殼值區分社團內節點時,取k=1,k=2,k=3,k≥4即可.整體而言,隨著k殼值的增大,可以劃分出的節點數量會有所下降;在社團規模較小時,較大k殼值的節點占比也可以達到很大(50%以上);但隨著社團規模的增大,不同k殼值節點占比也趨于穩定,k值取1,2,3時,3種情況涉及的節點占比都在30%左右.而本文采用k殼值劃分匹配社團內節點的初衷就是希望降低節點規模較大社團在匹配函數過程的計算量.從這個角度分析,可以得出結論,k殼值適合用于劃分節點規模較大的社團. 5.4.6 社團內節點地址分布的局部性 4.3節提出猜想,對于社團檢測算法檢測出的固件社團,其社團內的節點地址分布較為密集. 本文對數據集T1所有固件檢測出的社團計算了索引方差,并根據各社團的規模,通過隨機抽取索引,對每個社團進行20次仿真評估,計算其索引方差.繪制實驗結果如圖18所示. Fig. 18 Locality of node address distribution in the community 圖18(a)是社團規模、社團方差、社團方差的累積分布關系圖.其中,x軸為社團相對大小(社團節點量相對固件節點量),y軸為社團方差,z軸為固定大小的社團的方差累積分布值(即所有方差小于等于y值的概率的和). 圖18(b)是在圖18(a)的結果中隨機抽取了20個社團繪制的累積分布圖,以便于讀者觀察. 通過圖18可以看出,BGLL算法檢測的社團,在方差值更小的情況下,具有遠高于隨機選擇社團的累積概率,說明BGLL識別社團的局部性優于仿真結果.雖然對于個別社團,可能存在BGLL識別社團的方差高于隨機仿真結果的情況,但就整體而言,基于BGLL算法識別的社團,其方差普遍低于仿真結果,且幅度差別較大.說明BGLL識別社團內的函數地址存在局部性. 5.4.7 社團匹配的參數選擇 本節討論社團匹配最大差異度閾值β對社團匹配效果的影響. 對于數據集T2,β取0.05,0.1,0.15,0.2,0.25,0.3,0.35共計7個值,分析參數變化對社團匹配效果的影響.實驗結果如圖19所示. Fig. 19 The influence of parameter selection on community matching effect 圖19(a)是不同參數下不同大小的匹配社團節點占固件的比例.圖19(b)是不同參數下不同大小的匹配社團占總社團量的比例. 根據圖19不難看出,隨著最大差異度閾值的增大,匹配社團節點量在增加,但小社團的增加并不明顯,主要增加的是大社團.因此,應當盡可能取較大的差異度閾值.但就人工經驗而言,0.35已經是可以接受的上限,因此本文推薦β=0.35. 5.4.8 函數匹配的參數選擇對匹配效率的影響 本節探討函數匹配過程中,閾值γ和ε的選擇對函數匹配效率帶來的影響. 定義15.匹配效率.對于1對完成匹配的固件,其匹配效率η為 η=NMatched/t, (34) 其中,NMatched是匹配函數總的節點數量,t是總時耗. 對于數據集T2,γ取0.4,0.5,0.6,0.7和ε取0.05,0.10,0.15.形成12組參數組合,每種情況都進行1次實驗,統計不同參數組合條件下的函數匹配效率(定義13). 實驗結果如表2所示.實驗表明,隨著2個參數的增大,函數匹配數量的效率會有所下降. Table 2 Influence of Parameters ε and γ on Function Matching Efficiency 5.4.9 函數匹配的參數選擇與Bindiff比較實驗 本節探討函數匹配過程中,閾值γ和ε的選擇對函數匹配結果的準確率帶來的影響,并與Bindiff5的匹配結果進行比較. 實驗結果如表3所示.Ns表示本文方法與Bindiff判別結果相同的函數對數量.Nd表示本文方法與Bindiff判別結果不同的函數對數量,在這部分不同的結果中,存在部分函數對的匹配結果不隨參數ε和γ變化而變化,本文稱這類函數對的匹配結果為基本差異結果(數量為Nd_com),并將之列入表格最后一行.Nd_i表示本文方法與Bindiff判別的不同結果中,各參數特有的函數對匹配結果的數量,其計算為 Nd_i=Nd-Nd_com. (35) 對于本文方法與Bindiff判別結果不同的函數對需要進行人工核驗,以估算本文方法的識別準確率.對于基本差異結果,抽樣80對函數進行核對,樣本量為80;對于差異匹配結果中非基本差異部分,每組參數中抽樣20對函數;共計320對函數.核驗結果包括4種情況,本文方法正確的函數對數量TO;Bindiff正確的函數對數量TB;本文方法與Bindiff都錯誤的函數對數量Wr;人工無法判別的函數對數量Un. 為了評估本文方法和Bindiff的匹配效果,本文設計可信匹配率并使用準確率增量進行評估.對于本文方法的可信匹配率RCM_O,Bindiff的可信匹配率RCM_B和用本文方法修正Bindiff結果的準確率增量ΔU,其公式如式(36)~(38): (36) (37) ΔU=RCM_O-RCM_B, (38) 其中,NT2為T2數據集的函數對數量(21 990 414對),Sp,c為基本差異結果抽樣的樣本量,Sp,id為非基本的差異結果抽樣的樣本量,TO_c表示基本差異結果抽樣中本文方法正確的結果數量,TB_c表示基本差異結果抽樣中Bindiff正確的結果數量,TO_id表示非基本差異結果抽樣中本文方法正確的結果數量,TB_id表示非基本差異結果抽樣中Bindiff正確的結果數量. Table 3 Comparison of Bindiff Matching Results with the Matching Results of This Paper 對于評估指標的設計和實驗結果的分析如下: 1) 本文設計可信匹配率作為評估指標,僅對匹配函數對進行分析,而沒有直接使用準確率等包含未匹配函數的傳統指標.其主要原因在于2點:一方面,未匹配函數不適合列入統計.固件比對是一種較為嚴苛的場景,需要盡可能降低誤匹配.對于多數的二進制比對方法而言,未匹配并不僅僅是某個函數在對應文件中不存在匹配函數,也可能是函數可匹配的目標函數不只1個,但為了保證匹配函數中誤匹配的比率盡量低,而放棄這部分函數的匹配,將其列入未匹配結果,等待其他方法加以解決.另一方面,就2種比對方法進行分析比較而言,新方法對老方法的匹配結果應當帶來某種提升,而直接使用準確率進行評估未必能帶來最好的效果.一般而言,隨著匹配函數數量的不斷提升,用于進行函數相似性分析和傳播算法的時間開銷會不斷增大,但匹配結果中誤匹配的比率也隨之增大,此時,新方法修正老方法的可能性也隨之降低,經濟性(新方法運行單位時間開銷可修正的誤匹配結果數量)不斷下降. 結合上述2方面原因,不難發現,一個方法即使準確率低于另一種方法,也存在提升其他方法準確率的可能. 因此,使用準確率等傳統指標并不適用于衡量和評估本文的應用場景. 本文提出可信匹配率指標,其邏輯在于,對于2種方法一致的結果,基本可以視為可信結果;對于差異結果,通過人工核驗確定其中的正確部分,可推算匹配正確的比率;最終,可以推定被比較對象(固件對)的相似性下限.而通過計算2種方法可信匹配率的差異(即ΔU),依然能得到用一種方法的分析結果修正另一種方法分析結果后可提升的準確率. 2) 本文方法的12組參數實驗與Bindiff比較的基本差異結果有1 110 101對函數,約占數據集T2函數總量的5%.通過抽樣和人工核驗,其中93.75%的結果是本文方法正確,而僅有2.5%的結果是Bindiff正確.由此估算,使用本文方法,不論參數如何變化,至少可以為Bindiff帶來約4.6%的準確率提升.這是本文方法效果的下限. 3) 對于本文方法12組參數差異結果中非基本差異結果部分,參數的變化會帶來較為明顯的變化.γ<0.7時效果相對理想,隨著γ值的降低,會帶來更多的差異匹配結果;而隨著ε的增加,差異結果數量會增加;對于任何參數,其抽樣核驗的數據表明,本文方法對于非基本的差異結果正確的概率至少有70%,而Bindiff的正確的概率低于10%. 12組參數的實驗結果表明,使用本文方法修正Bindiff比對結果,可以提升5%~11%的準確率.總體而言,ε/γ取0.10/0.5,0.15/0.4,0.15/0.5是較為理想的選擇,此時,匹配效率較高,帶來的準確率增量也較高.本文最終選擇的參數為0.10/0.5. 此外,雖然受參數選擇和抽樣對象變化的影響,可信匹配率的計算結果也有不同,但依舊可以確定數據集T2至少有3成的函數是匹配的,可以證明實驗用的固件確實有一定的相似性. 5.4.10 操作數相似性與函數相似性關系 4.1.2節中提及,操作數相似性與函數相似性具備一定關系,現進行實驗分析如下. 針對數據集T2進行相似性分析,將分析過程中所有計算過的函數對的函數相似值和操作數相似值進行記錄,并繪制如圖20所示: Fig. 20 The relationship between operand similarity and function similarity 圖20(a)是函數的偏移量相似性Poff與函數相似性Sim(fi,fj)對應關系的散點圖;圖20(b)是函數的立即數相似性PImmi與函數相似性Sim(fi,fj)對應關系的散點圖. 從圖20中不難看出,雖然圖20中散點分布較廣,但其分布基本滿足函數相似性隨偏移量相似性和立即數相似性增加而增加的關系.在偏移量相似性和立即數相似性較低時,對應的函數相似值較高的情況相對少,反映在圖20中為函數相似值高的點相對函數相似值低的點分布更為稀疏. 對于立即數相似性和偏移量相似性較高的情況,最大函數相似值與立即數相似性和偏移量相似性的值存在線性關系,說明無法達到理論最大相似值為1的原因主要是操作數相似性不足造成的.驗證了前文的推斷,固件升級往往帶來函數操作數的變化,無法保證操作數穩定. 因此,在計算函數相似性的過程中,既要融入操作數相似性的特征,又不能賦予操作數相似性過高的權重以至拉低匹配函數整體的相似值. 5.4.11 未匹配區間長度分布 本節對相似性分析的未匹配區間大小進行分析.實驗選擇T2數據集,參數ε/γ取0.10/0.5.在進行相似性分析后,繪制不同固件節點量下未匹配區間長度的累積分布圖,如圖21所示: Fig. 21 Cumulative distribution graph of the number of firmware nodes and the length of the unmatched interval 其中,對于1對未匹配區間(i,j)和(i′,j′),若j=i+1,j′>i′+1,長度取j′-i′,標記為Insert;若j>i+1,j′=i′+1,長度取j-i,標記為Delete;若j-i=j′-i′,長度取j-i,標記為Equal;若j-i≠j′-i′,長度取區間長度均值,標記為UnEqual-Mean. 上述4種情況中,前2種一般意味著一段連續未匹配函數在固件升級過程中是新增或刪除的函數;第3種情況,一般是固件升級過程中函數結構變化較大,但函數數量變化不大,區間內的函數往往具有一一對應的關系.此3種情況,通過累積分布可以看出,一般區間長度都在100以內,量級為101. 而對于4種情況,其反映的是未匹配區間有函數數量差異的情況,一般是功能模塊有較大改動或者未匹配區間的邊界函數本身就不屬于同一功能模塊;其累計分布曲線也明顯不同于其他3種情況,未匹配區間平均長度可以達到103~104. 籍此可以說明參數τ選值10在量級上有其合理性.此外,需要說明的是,固件函數數量對于未匹配區間的累計分布大小并無明顯影響,說明相似性分析后的未匹配區間大小分布相對穩定. 5.4.12 匹配社團對節點匹配的貢獻 本節對不同規模的匹配社團對匹配節點的貢獻進行分析. 實驗使用數據集T2,實驗結果如圖22所示.其中x軸表示匹配社團占總社團數量的比例,y軸表示社團內包含的匹配節點占固件節點的比例. Fig. 22 The relationship between the proportion of matching communities and the proportion of matching nodes 本節實驗表明,節點規模介于100~1 000之間的社團在總節點量和社團數量上相較于其他2個規模的社團,既不是最高的也不是最低的.但是在貢獻的匹配節點比例上,明顯低于其他2個規模的社團,低了1~2個數量級. 對于這種現象,本文嘗試給出解釋.本文選擇的數據集具有一定的特殊性,其中的固件屬于同一廠商,基本都包含升級關系.造成上述現象的可能原因是固件在升級過程中,函數變化主要發生在節點規模在100~1 000的功能模塊內.節點規模較小的功能模塊功能單一且穩定,一般優化的價值不大.而節點規模在1 000以上的功能模塊,功能過于復雜,一般不會輕易進行優化.這2類功能模塊如果本身變化不大,那么匹配量一定會較高.而對于節點規模在100~1 000的功能模塊,修改的成本不是特別高,也易于發現新的優化目標,因此函數相對不穩定,匹配節點比例就相對低. 1) 關于圖的選擇.本文選擇了FCG,而大量的相關研究中使用CFG.誠然,CFG可以提供直接、間接跳轉等多種關系,可以增加圖中的連邊;將FCG中的節點從函數替換為CFG中的基本塊,會保留更多的可用信息.但是,這會帶來更大的運算負擔.即便是使用粒度較粗的FCG,本文也依然需要進行圖的壓縮工作(見3.1節),以減小后續分析開銷,而CFG帶來的邊的激增會大幅增加時間開銷(3.2節已分析BGLL算法的時間復雜度與圖的邊數相關). 2) 關于本文方法適用性問題.本文方法面向的固件主要為Cisco IOS.該固件是較為特殊的一類固件,其整個操作系統的存在形態是一個可執行文件,因此才會導致固件函數數量較大.而目前存在的嵌入式設備中,存在其他形態的固件,固件解包后包含不同的可執行程序和文件(如Cisco IOS-XE),其代表就是基于Linux開發的各類嵌入式設備固件.對于后一類固件,由于沒有實驗數據,不盲目推測本文方法的應用效果.從邏輯上講,后一類固件的可執行程序也必定包含不同的功能模塊,使用社團檢測應當會具有效果.但,從使用前提上講,社團檢測一般是面向復雜網絡的,如果程序內的函數數量規模不夠大,使用此法未必是最優選擇.畢竟,函數規模較小時,1.1節中提到的問題發生概率也較低. 本文提出了一種基于社團檢測的固件比對方法.首先,分析了自建數據集中固件FCG的性質.而后,提出了面向社團檢測的FCG壓縮算法,設計了社團表示和匹配方法,可在使用BGLL對固件FCG進行社團檢測后匹配社團.最后,基于匹配社團完成函數匹配,包括函數誤匹配修正和殘余函數匹配.此外,本文優化了函數相似性度量方法,引入了操作數相似性.通過實驗,驗證了本文方法的可行性,確定了文中參數的合理取值,并與Bindiff的比對效果進行比較.實驗結果表明,本文提出的基于社團檢測的固件比對方法可以提升Bindiff比對結果5%~11%的準確率.因此,本文的方法是可行且有效的. 作者貢獻聲明:肖睿卿負責形成研究思路、原型系統主體實現、實驗設計和具體實現、實驗數據整理和分析、實驗結果可視化,撰寫初稿;費金龍完成原型系統功能優化,降低實驗成本;祝躍飛負責理論模型構建、理論可行性分析;蔡瑞杰協助完成匹配社團相關參數選擇;劉勝利提出研究問題,確定研究思路,對實驗進行監督和領導,審閱和修改初稿.4 基于匹配社團的函數匹配方法
4.1 函數相似性度量方法
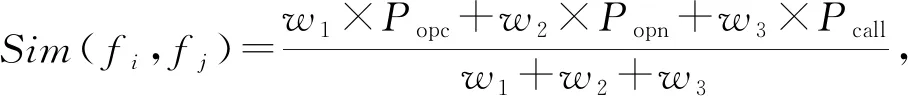
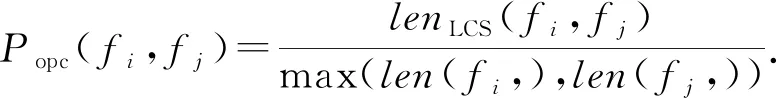
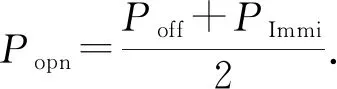
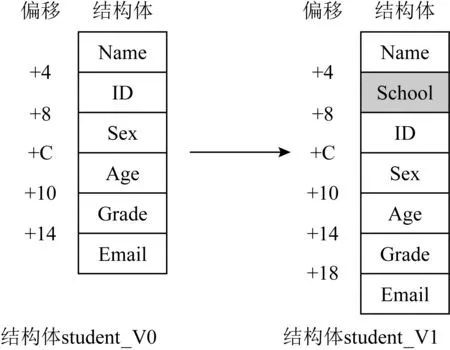
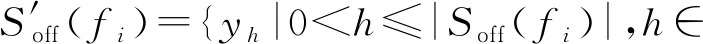

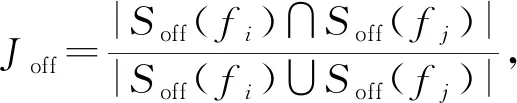
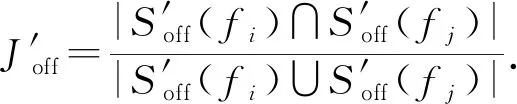
4.2 匹配社團的函數匹配
4.3 誤匹配函數修正

4.4 殘余函數匹配
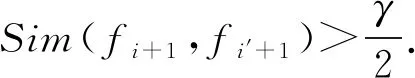
5 實驗與結果
5.1 實驗環境
5.2 數據集
5.3 預處理
5.4 實驗與分析
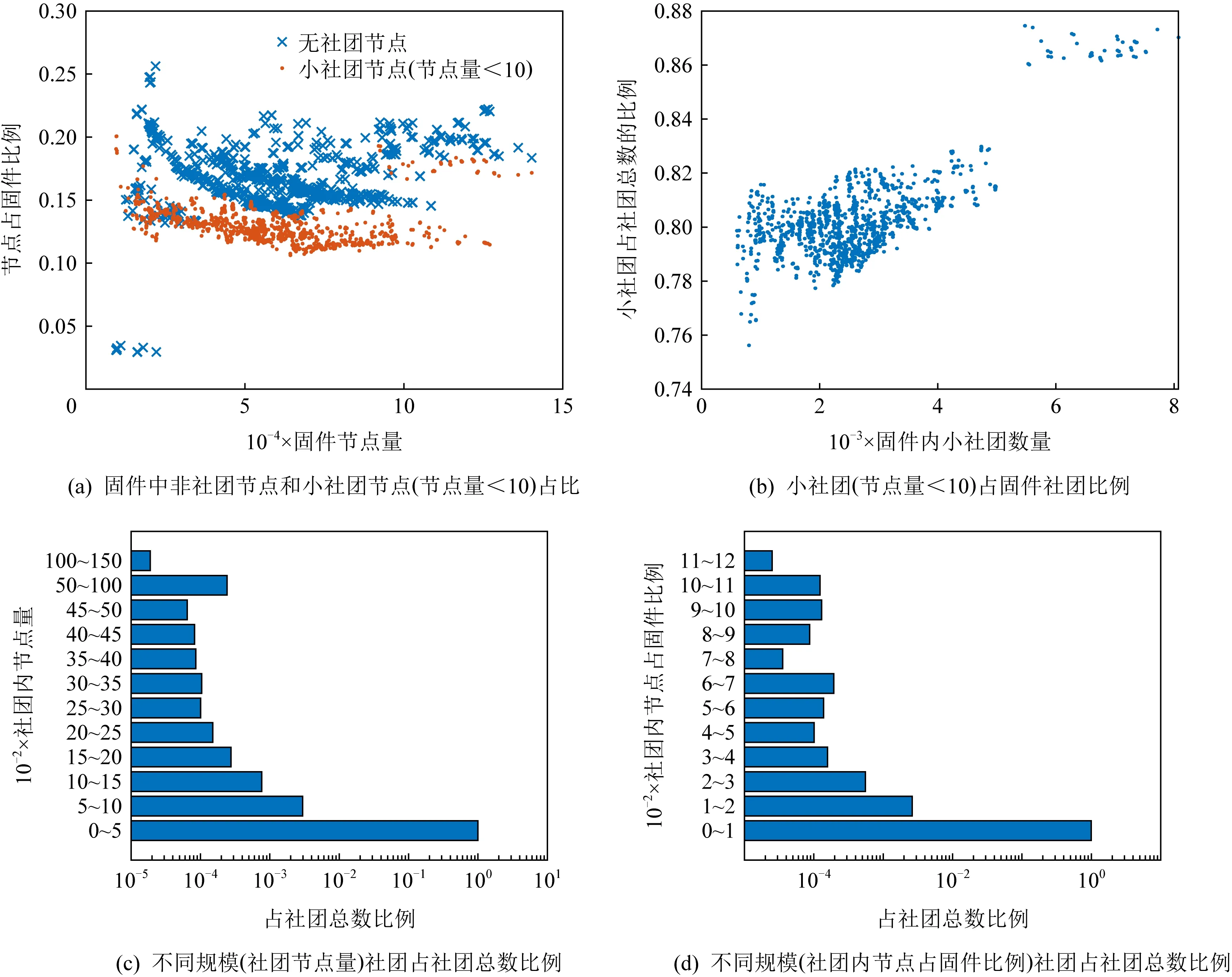
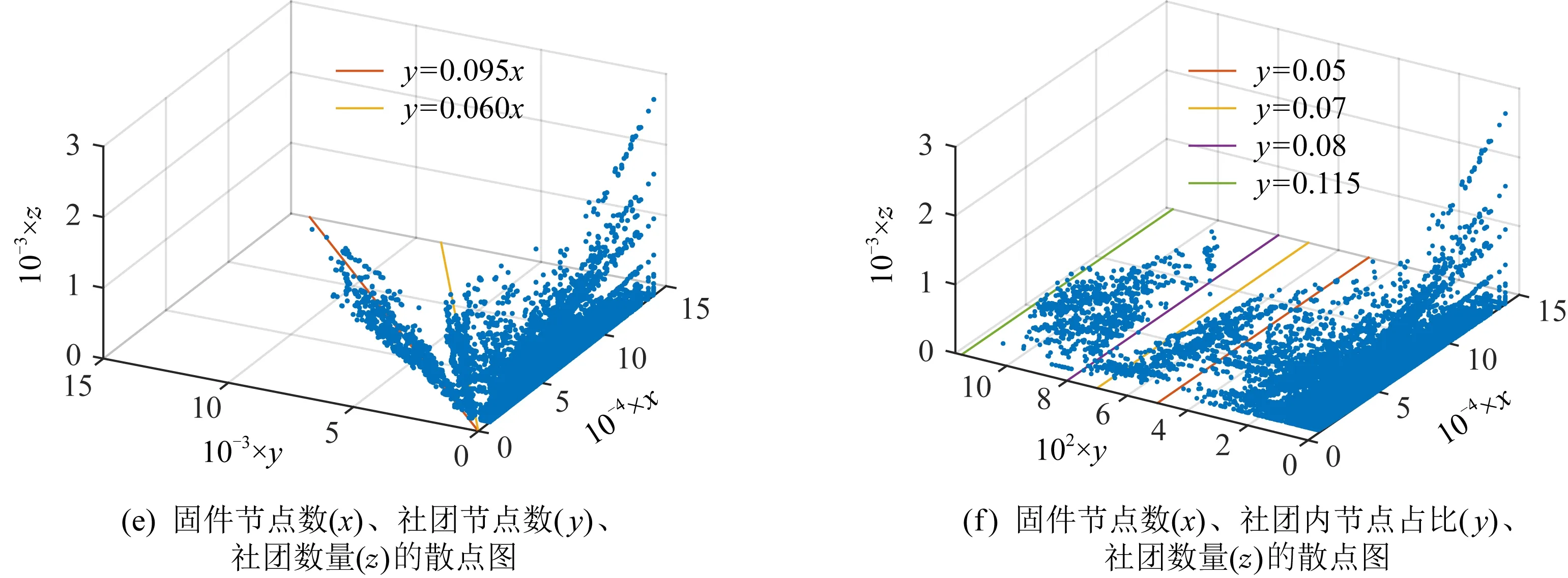
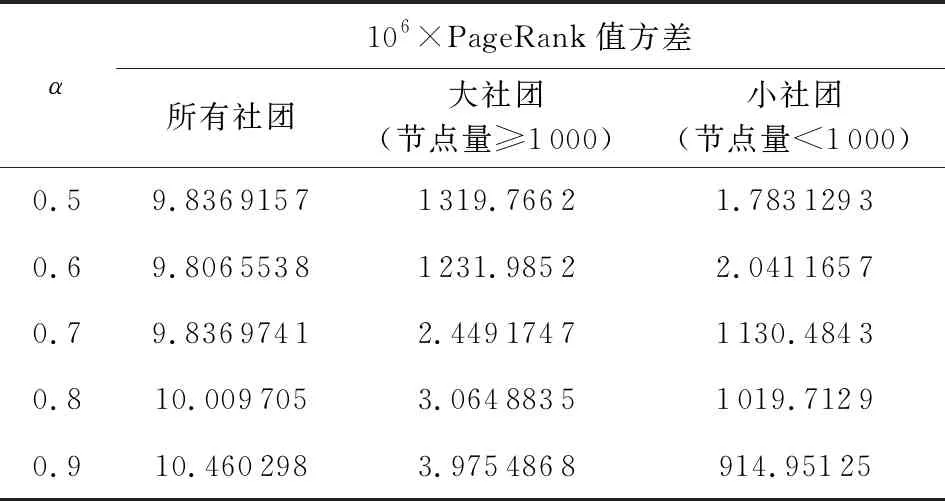
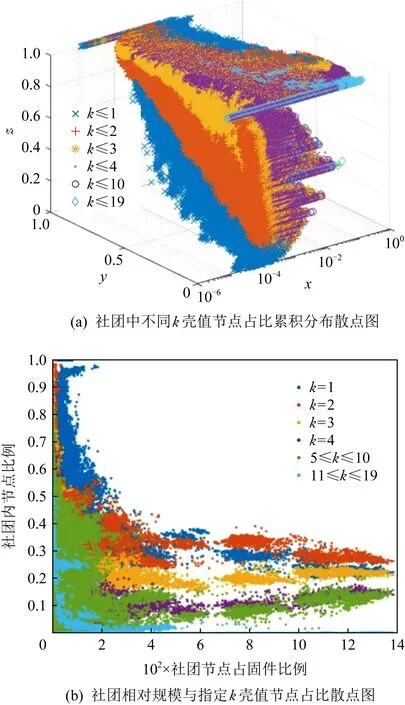
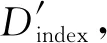
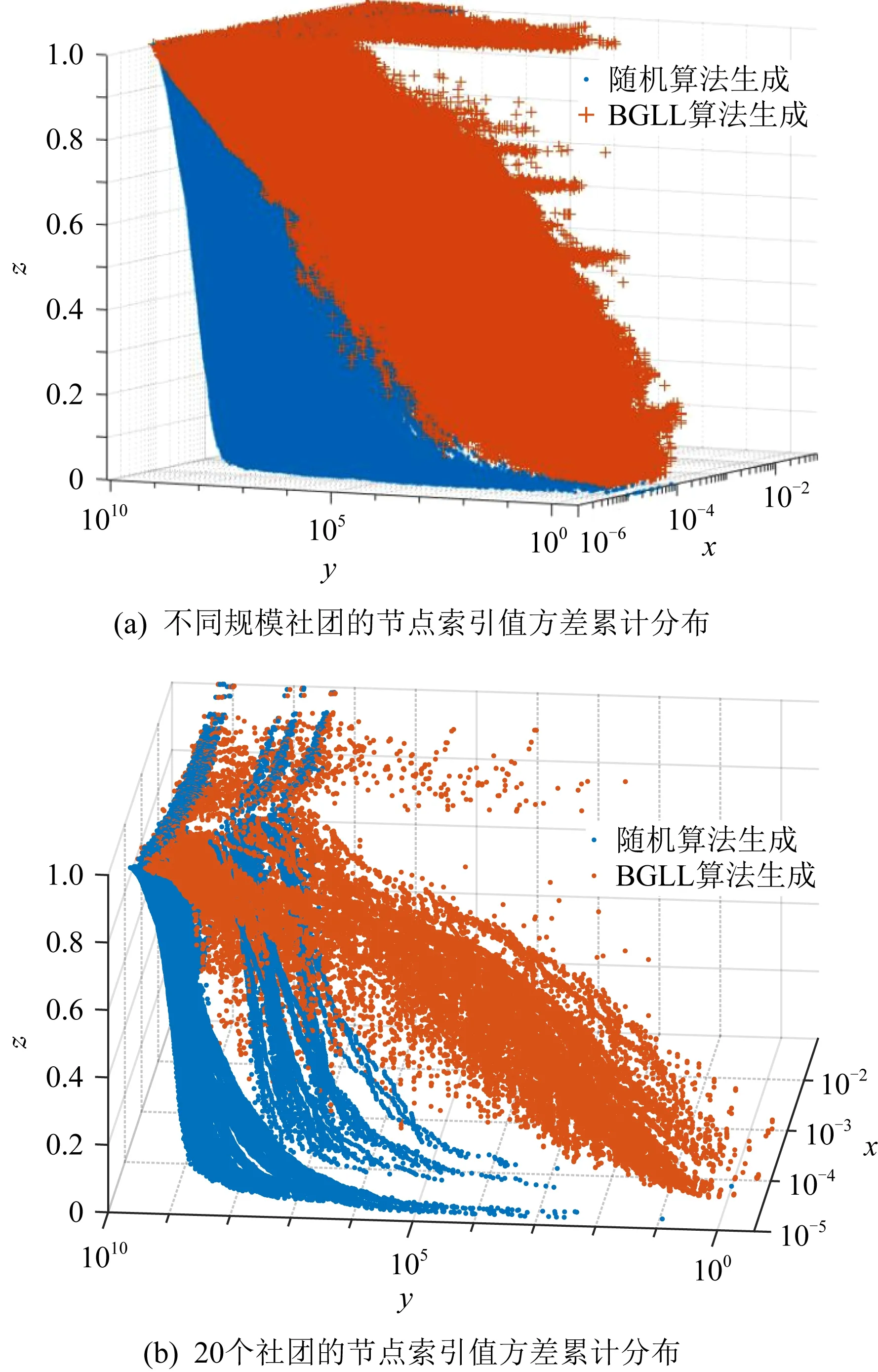
6 討 論
7 總 結

