面向多分類自閉癥輔助診斷的標記分布學習

章楓葉欣，王 駿，賈修一，潘 祥，鄧趙紅，施 俊，王士同

1.江南大學 人工智能與計算機學院，江蘇 無錫214122

2.上海大學 通信與信息工程學院，上海200444

3.南京理工大學 計算機科學與工程學院，南京210094

自閉癥譜性障礙（autism spectrum disorder，ASD）是一系列復雜的神經發展障礙性疾病，其臨床表現主要為社會交往障礙、言語交流障礙和動作刻板重復等。美國疾控中心數據統計顯示，美國兒童的自閉癥患病率高達1∶59。這表明自閉癥已經成為一個相當嚴重的健康問題，迫切需要開發一種有效的方法進行及時診斷。但是由于自閉癥的生理原因并不明朗，醫學診斷只能根據患者的癥狀及反饋、定性/定量的檢測信息、醫師的個人經驗等，具有很大的不確定性。因此，借助計算機進行自閉癥的輔助診斷具有重要的意義。

研究表明，自閉癥譜系障礙與患者的腦功能異常有關，而通過使用血氧依賴水平反映患者在靜息狀態下腦部代謝活動等功能性變化的靜息態功能性核磁共振圖像（resting-state functional magnetic resonance imaging，rs-fMRI）已成為量化大腦神經活動的有力工具，逐漸成為ASD 等腦部疾病研究的重要手段之一。以此為診斷依據，研究者們提出了多種借助計算機的自閉癥輔助診斷算法。如，Chen 等使用高階功能性連接矩陣進行自閉癥的輔助診斷，Aggarwal等提出多元圖學習進行自閉癥的輔助診斷，Heinsfeld 等通過深度學習探求腦區之間的相關性進行自閉癥的輔助診斷等。但是這些方法僅能處理二分類問題，而在臨床中，自閉癥譜性障礙包括若干與發育障礙相關的疾病，如自閉癥（autism）、亞斯伯格癥候群（Asperger's disorder）和無特異性的普遍發育障礙（pervasive developmental disorder not otherwise specified，PDD-NOS）等。已有的大多數自閉癥輔助診斷模型僅能解決二分類問題，無法同時區別ASD 的若干相關疾病。此外，這些方法也沒有對標記噪聲進行有針對性的處理。

標記噪聲是多分類ASD 輔助診斷涉及的一個挑戰，對分類器性能有著嚴重的不良影響。標記噪聲指訓練樣本的目標標記和對應實例的真實標記的偏差。標記噪聲的產生有多方面的因素，例如：標注過程中具有主觀性，待標記樣本本身可辨識度低，通信/編碼問題等。在自閉癥診斷場景中，標記噪聲普遍存在。診斷過程中的主觀性，診斷標準的不統一以及ASD 各子類的界限模糊這些特點造成了標記噪聲。

高維特征下的類不平衡問題是多分類ASD 輔助診斷涉及的另一個挑戰。通常用于ASD 輔助診斷的神經影像數據動輒成百上千個特征，加之訓練樣本數目非常有限，在進行分類器訓練時容易導致過擬合問題。而且用于構造ASD 分類器的樣本存在類別不平衡問題，導致分類預測結果往往偏向多數類。

針對上述問題，本文提出了一種代價敏感的標記分布支持向量回歸學習來進行ASD 的輔助診斷。首先，多分類ASD 輔助診斷面臨著標記噪聲問題，而標記分布獨有的標記形式，通過不同標記對于同一樣本的描述度，能夠更好地克服標記噪聲對分類器的影響，從而精確表達標記之間的相關程度。這就使學習過程蘊含了更加豐富的語義信息，可以更好地區分多個標記的相對重要性差異，對ASD 輔助診斷中的標記噪聲問題有較好的針對性。同時，支持向量回歸引入了核方法，通過核方法的非線性映射，使得原始輸入空間中線性不可分的數據可以映射入一個線性可分的特征空間，提供更多的可鑒別信息。最后，為了克服類別不平衡問題，引入了代價敏感機制，通過引入現實中存在的不同類別的誤判代價的不平衡性，使得算法能在一定程度上適應實際應用的需求，較公平地對待少數類和多數類。

1 相關工作

1.1 標記分布學習

標記分布學習（label distribution learning，LDL）是近幾年興起的一種機器學習方法，它是在單標記和多標記學習的基礎之上，引入了標記分布的概念。在多標記的場景下，一個樣本如果與多個標記相關，這些標記對于該樣本的重要程度一般會有所區別，標記分布就是描述不同標記對于同一樣本的重要程度的標記形式。標記分布學習就是以標記分布為學習目標的一種機器學習方法，已經被應用于諸多領域。例如，Gao 等提出了結合卷積神經網絡和標記分布學習的深度標記學習（deep label distribution learning）算法通過人臉估計年齡，Zhou 等提出了基于普魯契克情感色輪（Plutchik's wheel of emotions）的情感分布學習（emotion distribution learning）算法來從文本中自動識別用戶的情緒狀態，Geng等提出了基于多變量標記分布（multivariate label distribution）的算法實現頭部姿勢檢測。但是用于腦疾病的輔助診斷目前尚未見報導。

1.2 標記增強

標記分布學習要求訓練數據包含標記分布信息。然而，現實生活中人們往往以單標記或多標記的形式來標記樣本，使得難以直接得到標記分布信息。盡管如此，這些數據的標簽中仍然包含標記分布的相關信息。標記增強通過隱含在不同樣本標記之間的相關性，強化樣本的監督信息，進而在標記分布學習中獲得更好的效果。例如，Xu 等提出了標記增強作為標記分布學習的輔助算法，用于挖掘訓練集中的蘊含的標記重要性信息，將原始的邏輯標記提升為標記分布，輔助標記分布學習。Shao 等提出了標記增強多標記學習（label enhanced multi-label learning）從邏輯標記中重建潛在的標記重要性信息來改善標記分布學習的性能。

2 面向ASD 輔助診斷的代價敏感的標記分布學習

2.1 符號表示

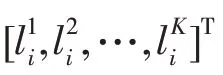
2.2 方法流程

本文提出的面向多分類自閉癥輔助診斷的標記分布學習算法，其流程如圖1 所示。首先，對rs-fMRI圖像進行預處理，在此基礎上構建功能連接矩陣，并基于功能連接矩陣得到每個樣本的功能連接特征向量。同時，結合邏輯標記數據和功能連接特征進行標記增強，獲得樣本的標記分布形式。最后，進行基于代價敏感的標記分布學習建模，從而得到面向自閉癥輔助診斷的多分類模型。

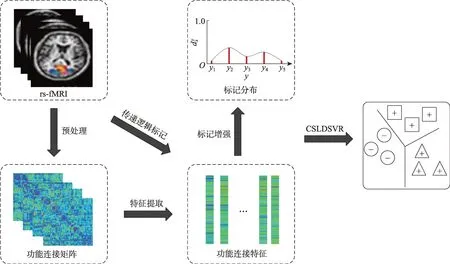
圖1 代價敏感的標記分布支持向量回歸的流程圖Fig.1 Flowchart of cost sensitive label distribution support vector regression

2.3 標記分布自閉癥輔助診斷數據集的獲取

標記分布學習通過引入描述度來刻畫每個標記和樣本的相關程度，因此它可以從數據中得到比多標記更加豐富的語義信息，更加準確地表述同一個樣本的多個標記的相對重要性差異。然而，標記分布學習的基本要求是要有標記分布的數據集，這一點在現實中往往很難滿足要求。可以通過標記增強方法對給定的多標記形式樣本進行轉化得到標記分布形式數據。采用基于FCM（fuzzy C-means）和模糊運算的標記增強方法，基本思路如下：

（1）利用FCM 把個樣本分為個模糊聚類，并求每個聚類的中心，使得所有訓練樣本到聚類中心的加權距離之和最小，式（1）列出了具體的加權距離公式。

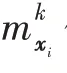
（2）構造標記和聚類之間的關聯矩陣，矩陣中的元素即代表了標記和聚類的關聯度，關聯矩陣的計算方法如式（2）。

式中，A為矩陣的第行，A即第個類的樣本的隸屬度向量之和，行歸一化之后，關聯矩陣可以視作一個聚類和標記的模糊關系矩陣。

（3）根據模糊邏輯推理機制，將關聯矩陣和隸屬度進行模糊合成運算，得到樣本對標記的隸屬度，歸一化后，即為標記分布。

基于FCM 和模糊運算的標記增強引入聚類分析作為橋梁，通過樣本對聚類的隸屬度和聚類對標記的隸屬度這兩者之間的復合運算，得到樣本對標記的隸屬度，即標記分布。在這一過程中，通過模糊聚類挖掘樣本空間的拓撲關系，并且通過關聯矩陣將這種關系投影到標記空間，從而使得簡單的邏輯標記產生了更豐富的語義信息，轉變為標記分布。

2.4 代價敏感的標記分布支持向量回歸學習

面向ASD 輔助診斷進行標記分布學習建模，需要重點考慮以下兩個關鍵問題：首先，ASD 數據樣本的各類分布不平衡。研究表明，在有監督的機器學習任務中，類別不平衡會對訓練產生不利影響。它既影響訓練階段的收斂，也影響測試集上模型的泛化能力。因此，本文在標記分布支持向量回歸的基礎上引入了代價敏感機制，從而平衡多數類和少數類對目標函數的影響。其次，ASD 數據集大多是多分類數據，而指導標記分布學習訓練的數據應該是標記分布的數據。為此，引入了標記增強，將每個訓練樣本的標記轉化為標記分布。標記增強的過程在2.3 節中有簡要描述。

假定樣本對應的標記分布可以由樣本在特征空間的投影線性表示：

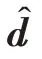
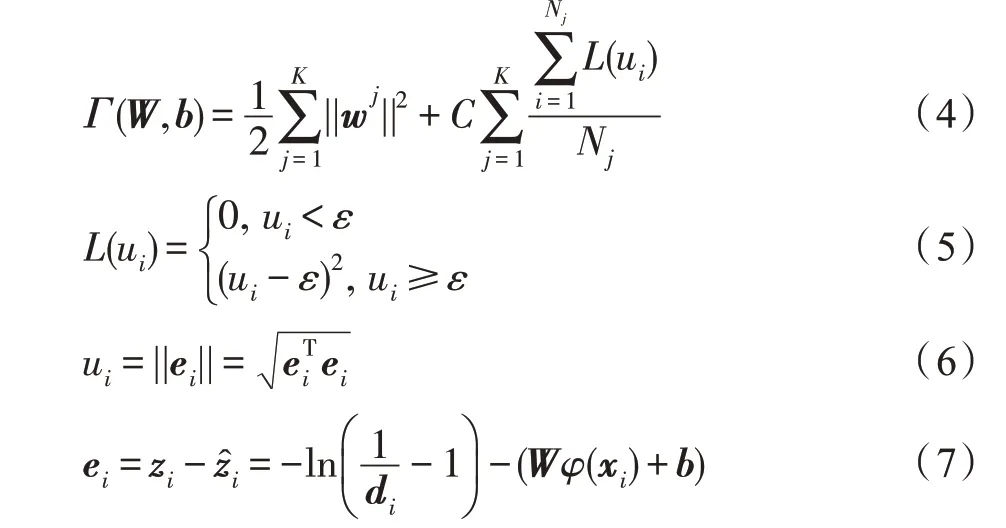
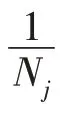
(u)是關于w、b的凸函數。

證明式（5）是凸函數，即證明(u) 關于w、b的二階導數恒大于等于0：

其中，(w,(x))是關于w、(x)的函數。顯然式（8）恒大于等于0，同理可證(u)關于b非負，定理得證。

本文使用擬牛頓迭代法（iterative quasi-Newton method）優化式（4）。首先，本文將式（4）的第二部分進行泰勒級數展開，取其線性部分作為近似值，在第次迭代中，近似值如下：

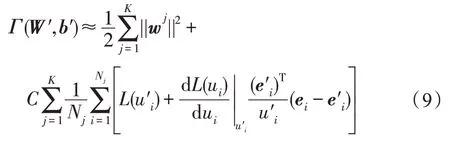
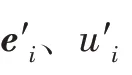
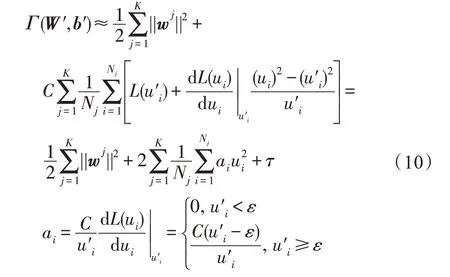
其中，是一個與,無關的常量。式（10）分別對w、b求偏導，并令偏導數的值為0，可以得到公式：

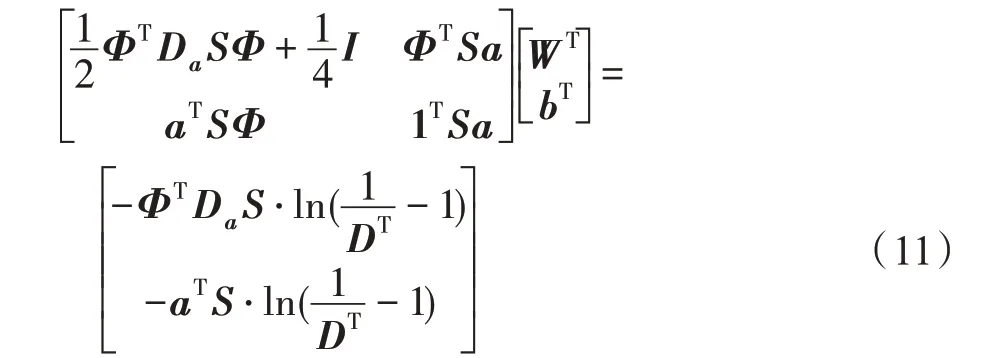
其中，K=(x,x)=(x)(x)，K為矩陣的第行第列的元素值，(x,x)即核函數。至此，將、代入式（3），預測函數可以更新為：

即可從樣本的輸入特征空間計算得相應的標記分布。標記分布的結果即ASD 及其子類對于同一樣本的重要程度，取最大可能標記作為結果：

CSLDSVR

輸入：自閉癥數據，標記分布，權重系數，核函數類型，不敏感區大小，核帶寬。

輸出：預測模型、。

3 實驗結果和分析

3.1 評估指標

本文同時使用標記分布的評估指標和多分類任務的評估指標進行算法評估。所有評估指標及計算公式如表1 所示，前六種為標記分布學習的評估指標，后兩種為多分類任務的評估指標。指標名后帶有“↑”表示數值越大，算法效果越好；帶有“↓”，表示數值越小，算法效果越好。

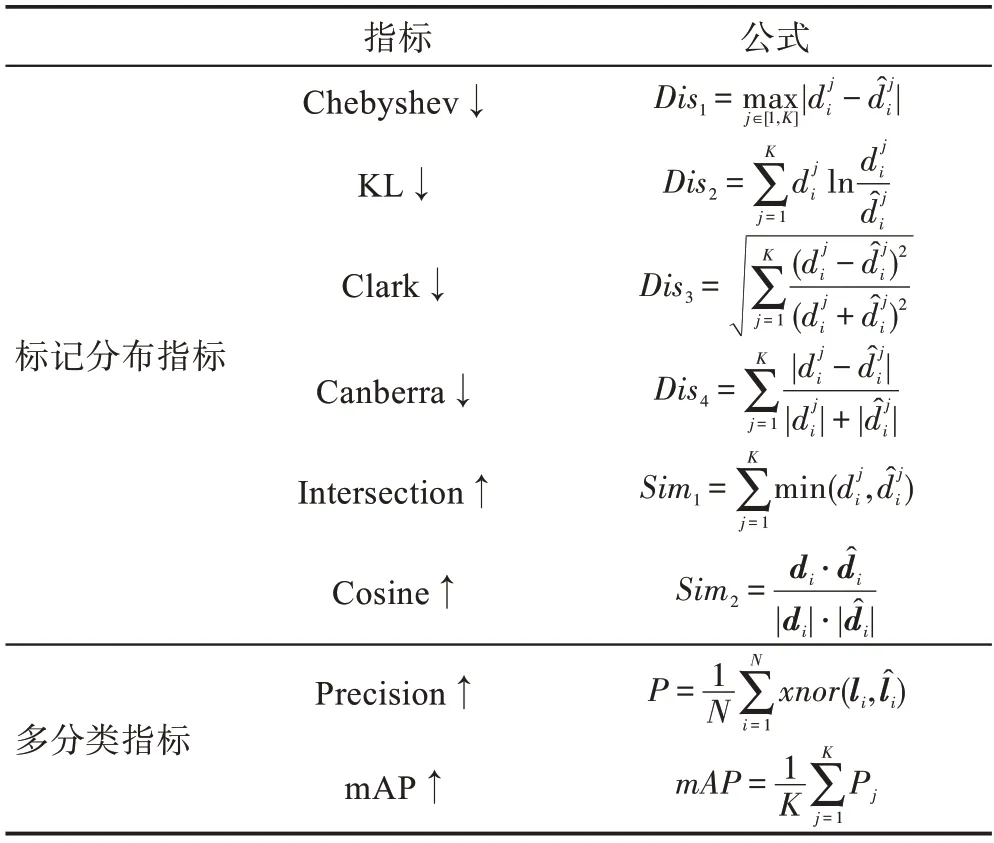
表1 評估指標Table 1 Evaluation measures

表1 中，P為第類的Precision，為異或計算，代表距離（Distance），代表相似度（Similarity），代表宏平均正確率（macro-averaging precision）。

3.2 數據集及預處理

本文使用的所有rs-fMRI 數據集均來自ABIDE網 站（Autism Brain Imaging Data Exchange，http://fcon_1000.projects.nitrc.org/indi/abide/）。表2 給出各數據集中各類樣本的組成情況。以NYU（New York University）數據集為例，NYU 數據集數據采集機構為紐約大學。采集過程中，被試者始終保持靜息狀態，不執行任何動作。具體參數如表2 所示。

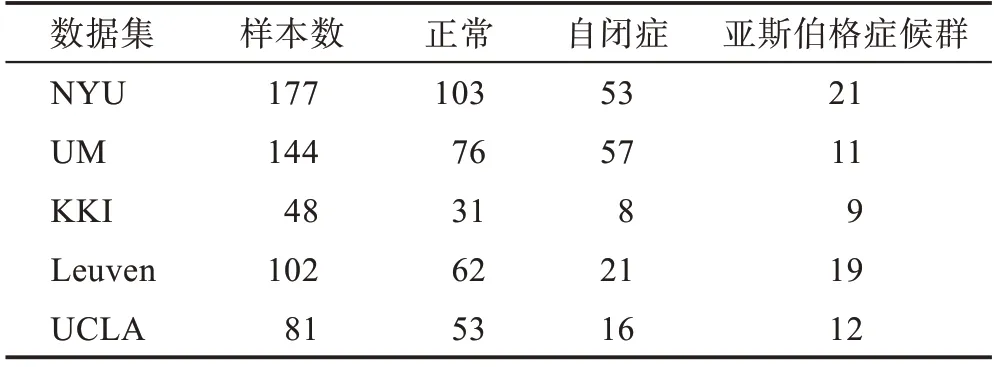
表2 數據集的統計信息Table 2 Statistics of datasets

表2 中，UM 代表密歇根大學，KKI代表肯尼迪克里格研究所，Leuven 代表魯汶大學，UCLA 代表加利福尼亞大學洛杉磯分校。

雖然大腦各腦區在空間上相互隔離，但它們之間的神經活動相互影響。本文使用腦區之間的腦功能連接矩陣作為分類特征。功能連接矩陣的計算步驟（即預處理步驟）如下：

（1）根據靜息態功能磁共振成像數據，使用DPARSF（data processing assistant for resting-state fMRI）工具提取出各腦區的平均時間序列信號，計算腦區之間的Pearson 系數，得到功能連接矩陣。

（2）將功能連接矩陣的每一行作為各腦區的特征描述，取功能連接矩陣的上三角陣，按行串聯，得到對應的特征向量。

3.3 對比算法

將提出的CSLDSVR 方法和6 個現有LDL 算法以及兩個多分類算法進行對比。兩個多分類算法為決策樹（decision tree）和最近鄰（-nearest neighbor，NN），這兩種算法均為經典的多分類算法。6 個現有LDL 算法為：PT-SVM、PT-BAYES、AA-NN、AA-BP（back propagation）、SA-IIS（improved iterative scaling）、LDSVR，其中，“PT”表示問題轉化（problem transformation），“AA”表示算法改造（algorithm adaptation），“SA”表示專用算法（specialized algorithm）。對比算法的具體說明如表3 所示。

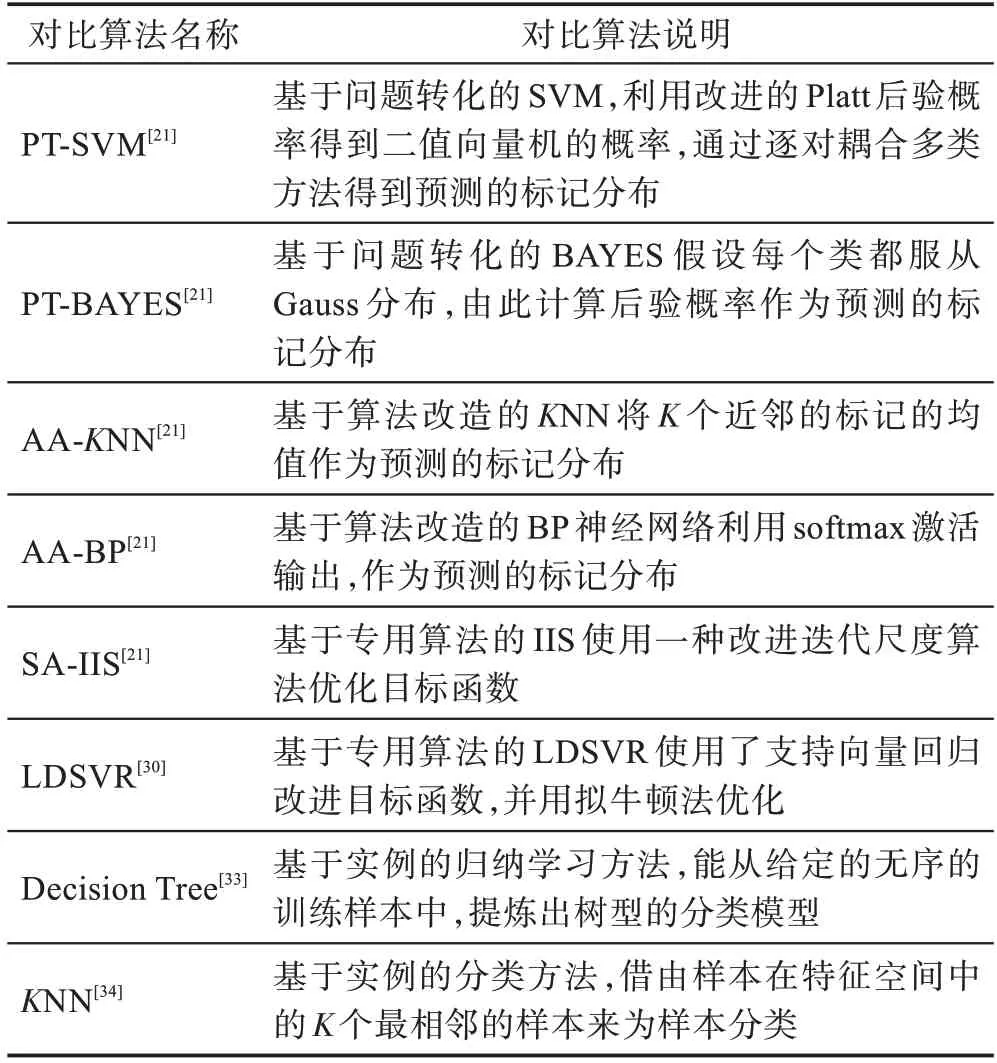
表3 對比算法Table 3 Comparison algorithms

本文提出的CSLDSVR 算法有4 個參數，即權重系數、核函數的類型、不敏感區大小、高斯核的核帶寬。參數具體的范圍如表4 所示。使用十折交叉驗證來計算結果。具體操作步驟如下：將數據集隨機劃分為10 等份，在每一折交叉驗證中，取1 份作為測試集，剩下9 份作為訓練集。重復上述過程10次，取10 次結果的均值作為評價指標。

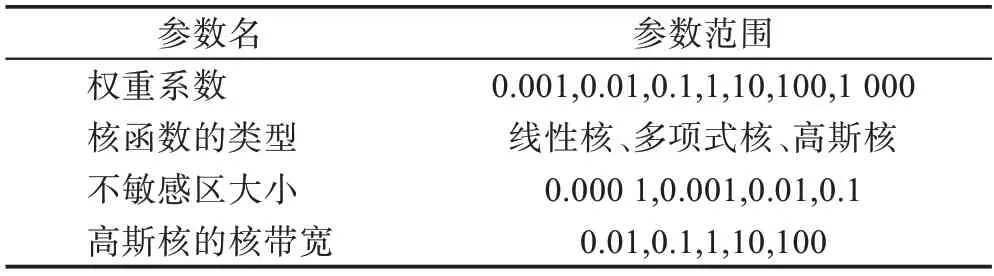
表4 參數范圍Table 4 Range of parameters

3.4 標記分布算法對比

表5 匯總了6 個標記分布學習算法和CSLDSVR在5 個不同的數據集上的實驗結果，實驗結果以均值±標準差的形式記錄。其中，加粗的為每一個指標在當前數據集上不同方法中的最佳數值。顯然可見，在和標記分布學習算法的對比中，CSLDSVR 在多數情況下都表現出了優異的效果，在UM、UCLA、KKI 數據集上更為明顯。在標記分布的指標中，KL散度是描述兩個分布的差異的指標，而且作為對比的LDL 算法都是以KL 散度作為目標函數的，CSLDSVR 的預測結果的KL 散度可以做到最小，說明新算法預測的標記分布總體上和真實數據分布最相近，優于對比算法。

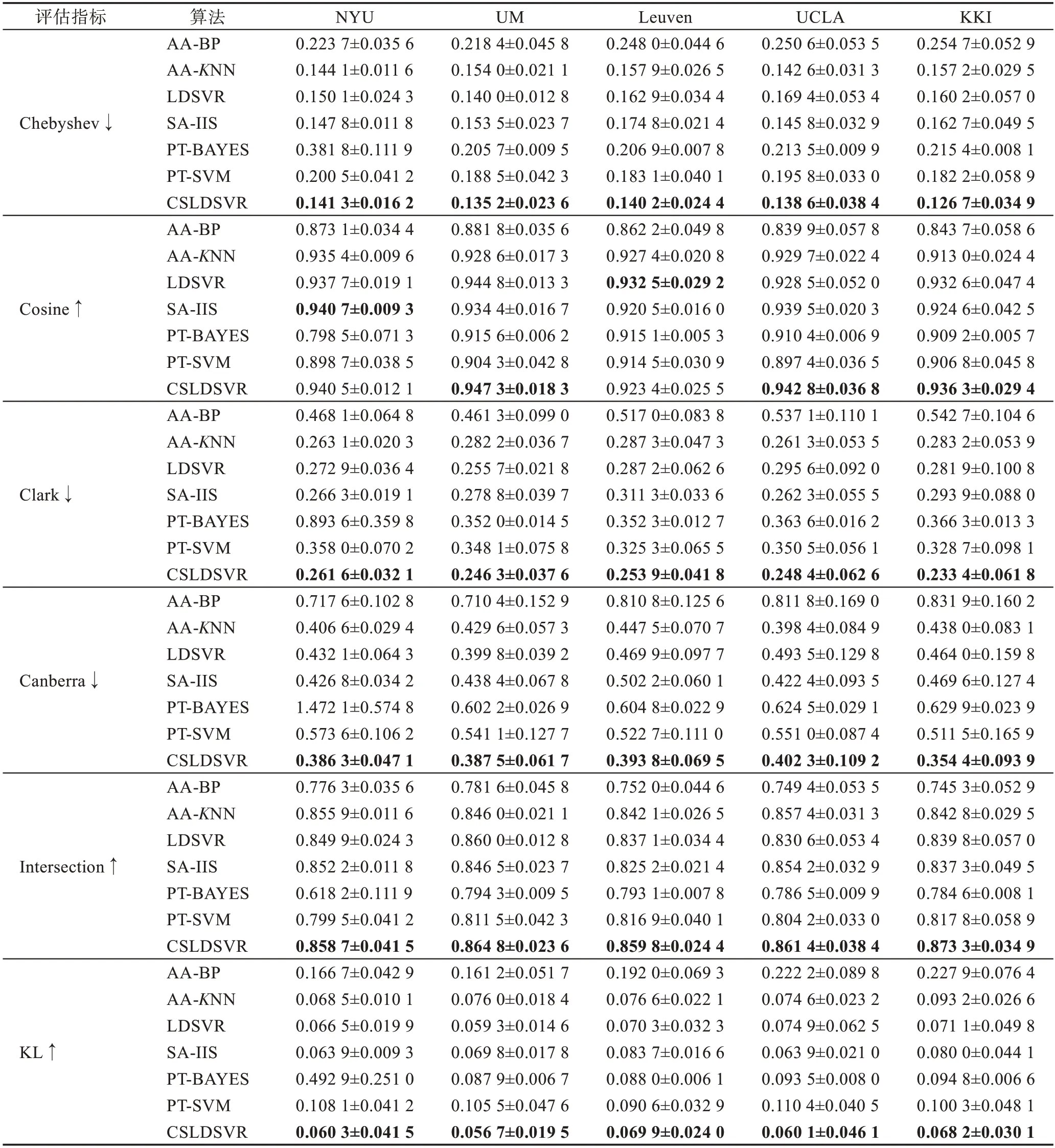
表5 CSLDSVR 和標記分布算法的性能比較Table 5 Performance comparison of CSLDSVR and LDL algorithms

圖2 匯總了CSLDSVR 和標記分布算法多分類指標Precision 和mAP 的結果，在最重要的兩個多分類指標上，CSLDSVR 都表現較佳。有些算法正確率高，宏平均卻很低，這是因為這些算法沒有考慮類別不平衡問題，模型分類偏向多數類。CSLDSVR 使用了核技巧，可以在更具有鑒別能力的特征空間中解決問題，而且CSLDSVR 考慮了每個類的大小，從而有效解決了因類別不平衡而帶來的問題。

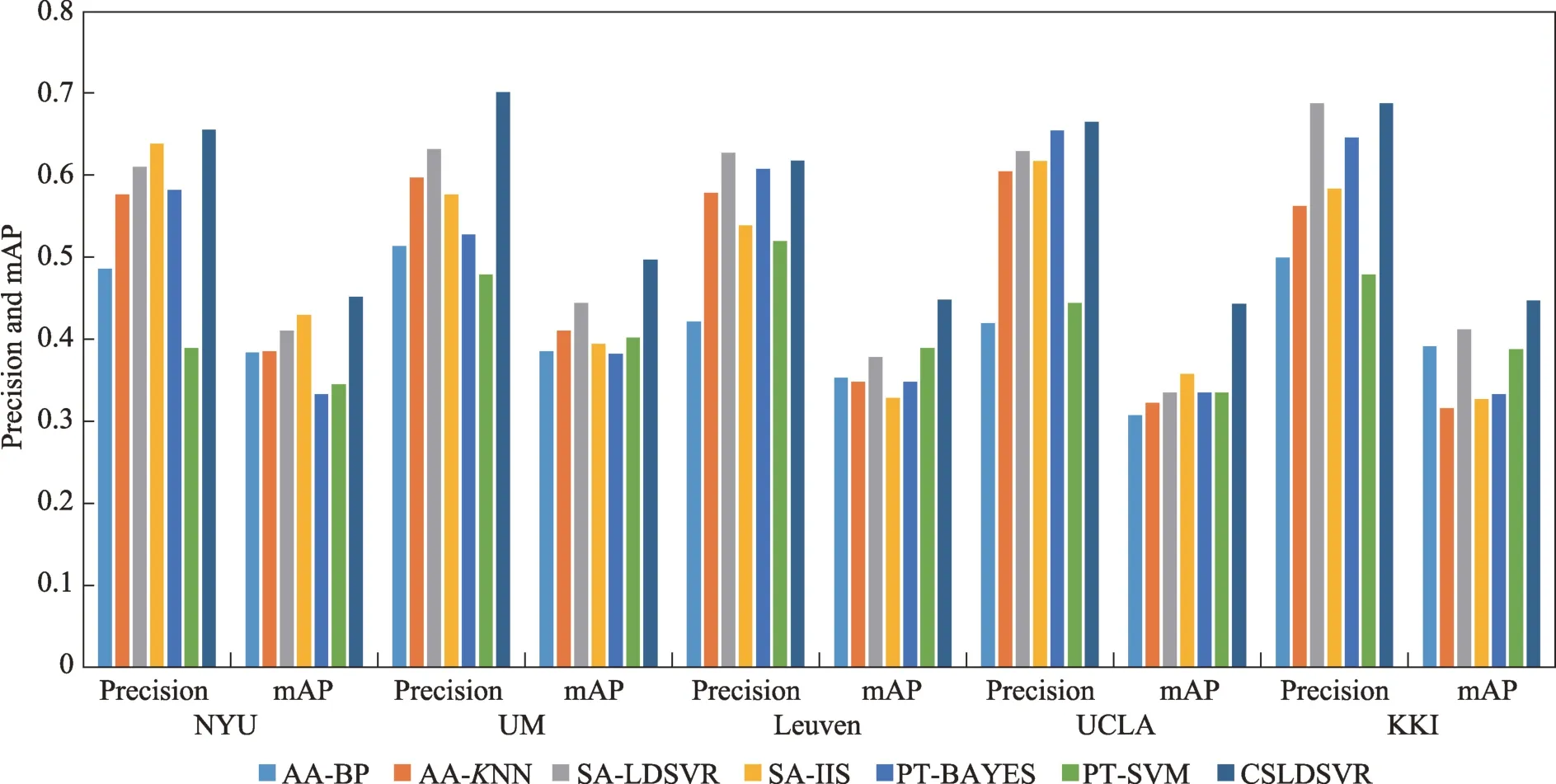
圖2 CSLDSVR 和標記分布算法的分類效果對比Fig.2 Comparison of classification performance of CSLDSVR and label distribution algorithms

為了驗證代價敏感機制對性能的提升，將本文算法與沒有代價敏感機制的LDSVR 進行對比。如表5 所示，在多數情況下，本文算法CSLDSVR 的學習效果較好；此外，結果的標準差基本都維持在一個較低的水準，即算法的穩定性有所提高。而LDSVR未引入代價敏感機制，算法所得結果的標準差較大且波動，例如在UCLA 和KKI的Canberra 指標標準差都超過了0.1。

3.5 多分類對比實驗

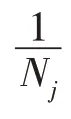
表6 CSLDSVR 和多分類算法的性能比較Table 6 Performance comparison of CSLDSVR and multi-classification algorithms

3.6 參數敏感性分析

本節研究參數的變化對算法CSLDSVR 性能的影響，圖3 給出了在5 個不同數據集上，參數、取不同值時，評估指標Precision 和KL 散度的變化。對照研究同一參數不同指標的兩張圖，例如圖3（a）和圖3（c），可以發現同一個數據集的曲線走勢基本是相反的，Precision 取最大值的點一般KL 散度也恰好為最小值，這也與前文對KL 散度的分析相照應，說明在KL 散度較小時，兩者的標記分布更為相似，分類的結果也更加準確。

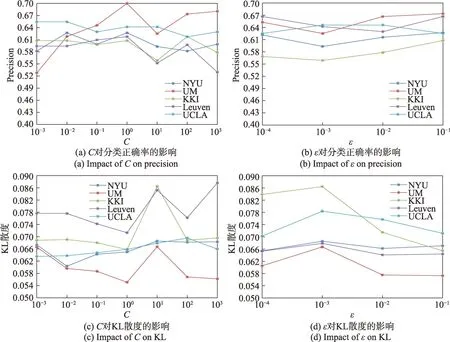
圖3 參數C、ε 在5 個數據集上的敏感度分析Fig.3 Sensitivity analysis of parameters C and ε on 5 datasets

發現對于不同數據集，取到最優解的參數值并不相同，這也表明了在自閉癥診斷中，不同數據中心的數據分布不同，構建模型的參數也應該不同。而且發現樣本數量越少的數據集，結果對參數的變化越敏感，例如僅有48 個樣本的KKI 數據集，在參數值變化時波動最大。

由此可見，CSLDSVR 算法的參數應針對數據集的特點，設定相應的參數值構建模型，在參數設置合理的情況下，CSLDSVR 可以克服自閉癥數據集的高維度和類別不平衡問題，取得更好的分類效果。

4 結論和展望

ASD 患者的腦功能異于正常人，而rs-fMRI 是反映大腦活動的有效工具，本文基于從rs-fMRI 中提取的功能連接特征，提出了一種代價敏感的標記分布支持向量回歸的ASD 輔助診斷方法。標記分布學習的引入，克服了基于多分類的ASD 輔助診斷的標記噪聲問題。而且新的方法在標記分布支持向量回歸的方法基礎上，引入了類別平衡，平衡了多數類和少數類對目標函數的影響。新的方法克服了多數類和少數類對結果的影響的不平衡性，可以有效解決ASD 診斷中的不平衡數據問題，但是改進模型還是一定程度地偏向多數類，要進一步地改善不平衡數據問題，可以嘗試改進數據的采樣方法或使用合成少數類樣本方法等，這值得進一步的研究；同時，損失函數可以改用更復雜的距離度量方式，歐氏距離平等對待每個特征，因此能夠體現個體特征數值上的絕對差異。但引入相對高級的距離也有其必要性，不過這需要更多的先驗知識。目前沒有使用更多的先驗知識，因此使用歐式距離。其他高級距離有其優勢，在今后的研究中將進一步改進本文工作。