單軸對稱截面橋墩彈塑性地震響應研究

王 巍

（廣州市市政工程設計研究總院有限公司，廣東 廣州510600）

0 引 言

近年來，城市橋梁的建設得到了飛速發展，與公路橋梁不同的是，城市橋梁不僅需要滿足交通功能，還要滿足城市景觀的要求。橋墩是橋梁結構的重要受力構件，也是橋梁外形構造的主要組成部分，而傳統的矩形截面方墩、橫向變寬花瓶墩等雙軸對稱截面橋墩已經不能完全滿足橋梁結構造型的需求，為了讓橋梁結構更加優美，現在的城市橋梁出現了較多異形截面橋墩，其中單軸對稱截面橋墩應用最多，其特點為橋墩截面僅有一條對稱軸，見圖1。

圖1 單軸對稱截面示意圖

目前，考慮非線性的橋墩地震響應研究集中在規則截面橋墩，對于異形橋墩，尤其是單軸對稱截面橋墩的地震響應研究文獻較少。本文基于OpenSees[1]軟件，采用彈塑性纖維梁柱單元建立墩柱模型，考慮上部梁體重量、隔震支座及材料非線性的影響，采用IDA增量動力分析法[2]對某單軸對稱截面橋墩進行了結構彈塑性地震響應分析，研究了單軸對稱橋墩的地震響應行為特征，對于指導該類橋梁設計具有一定的參考意義。

1 計算模型

1.1 模型簡介

基于OpenSees，建立某單軸對稱截面橋墩有限元模型，采用一根桿單元模擬橋墩，墩底固接，采用集中質量塊模擬上部結構梁體，梁體質量塊和橋墩之間通過彈簧連接模擬隔振支座，通過建立橋墩動力模型計算結構彈塑性地震響應，以研究不同墩高橋梁彈塑性地震響應及差異性。模型簡圖見圖2。

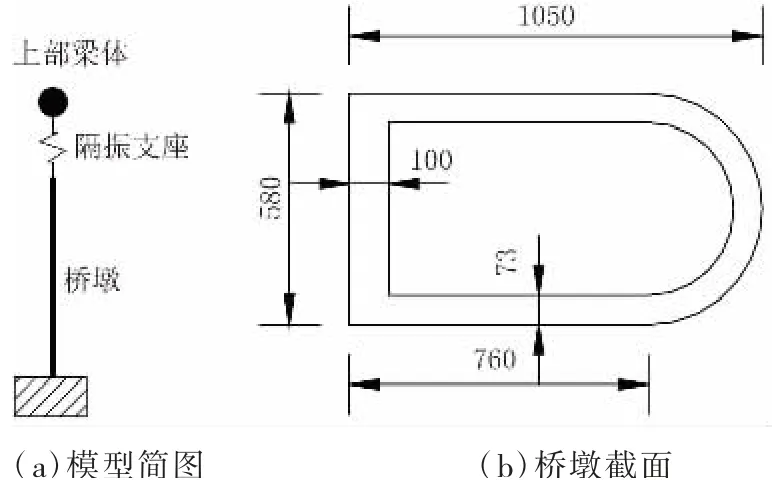
圖2 橋墩模型示意圖（單位：cm）

所采用的地震激勵時程見圖3，對應PGA=0.33g。

圖3 地震激勵時程圖

1.2 彈塑性纖維梁柱單元

采用彈塑性纖維梁柱單元，將單元截面離散成纖維，對于不同位置的纖維賦以相應的材料非線性應力—應變關系，不考慮剪切變形，假設纖維之間完全黏結且滿足平截面假定，扭轉剛度采用與彎矩、軸力均不耦合的彈性扭轉理論。

目前較成熟可靠、計算高效的纖維梁柱單元為基于柔度法的彈塑性纖維梁柱單元[3]。柔度法將力作為未知量，采用力插值函數建立單元的柔度矩陣；基于柔度法的彈塑性纖維梁柱單元對于假定的內力分布，無論單元及纖維處于何種狀態，平衡條件都能嚴格滿足，能夠更真實地反映結構中內力與變形的分布，不受單元材料非線性水平的影響和制約[4]。

1.3 彈塑性材料本構

鋼筋纖維采用考慮包辛格效應和硬化階段修正的Menegotto-Pinto本構[5]，其曲線方程見式（1）、式（2）：

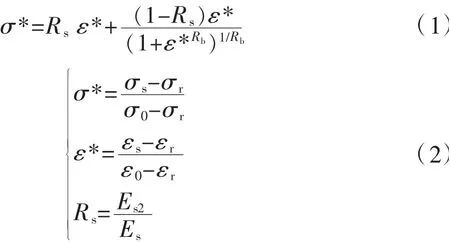
式中：Rs為應變硬化系數；Es、Es2分別為鋼筋的初始彈模和屈服后彈模；σr、εr分別為反向加載點的應力和應變；σ0、ε0分別為漸變線交點的應力和應變。

混凝土纖維采用考慮箍筋對核心混凝土約束效果的Mander本構[6]，其曲線方程見式（3）。

式中：fcc為約束混凝土的抗壓強度；x為約束混凝土的相對應變；r為約束混凝土應力-應變曲線系數。

1.4 墩頂位移IDA分析

增量動力分析（IDA）是通過采用不同系數將地面運動參數進行調整獲得一組地震動輸入，運用這組地震動輸入對結構進行非線性時程分析，最后繪制結構性能參數與地面運動參數的關系曲線的過程。本文中采用墩頂位移作為結構性能參數。

2 計算結果

2.1 墩頂位移的“雙彎曲”現象

橋墩墩底截面以及坐標系見圖4，在z方向輸入地震激勵得到的墩頂位移見圖5，在y方向輸入地震激勵得到的墩頂位移見圖6。

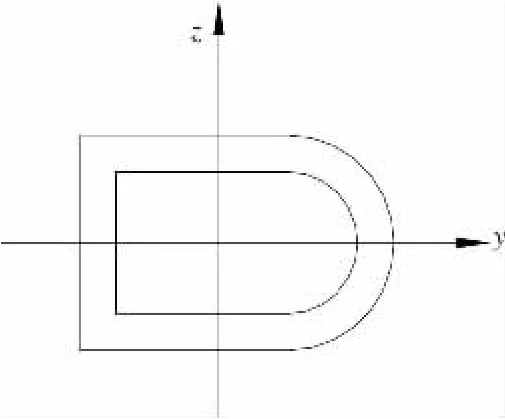
圖4 橋墩截面坐標系示意圖

由圖5、圖6可知，在z方向地震激勵作用下，墩頂z方向最大位移為0.341 m，y方向最大位移為0.112 m；在y方向地震激勵作用下，墩頂y方向最大位移為0.399 m，而z方向沒有產生位移，即單軸對稱截面的橋墩在對稱軸方向的地震激勵作用下，墩頂僅產生激勵方向的位移，在垂直于對稱軸方向地震激勵作用下，在對稱軸方向、垂直于對稱軸方向均產生墩頂位移，出現“雙彎曲”現象。

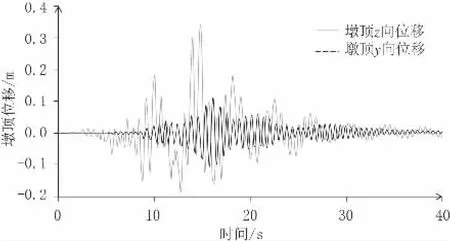
圖5 z向地震輸入墩頂彈塑性位移圖（單位：m）

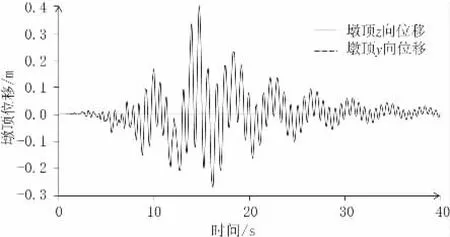
圖6 y向地震輸入墩頂彈塑性位移圖（單位：m）

2.2 “雙彎曲”現象原因分析及驗證

如圖7所示，在地震荷載作用前，截面的質心和形心重合，當沿著z方向施加地震激勵時，z方向截面邊緣的混凝土首先開裂，由于截面兩側混凝土不對稱開裂且截面關于z軸不對稱，導致有效截面的形心相對于質心不僅有z方向偏移，還有y方向偏移，從而導致橋墩質量產生的豎向動軸力對有效截面分別產生了兩個方向的附加彎矩和，在垂直于激勵方向的附加彎矩作用下，橋墩產生了垂直于激勵方向的地震響應，從而出現“雙彎曲”現象。

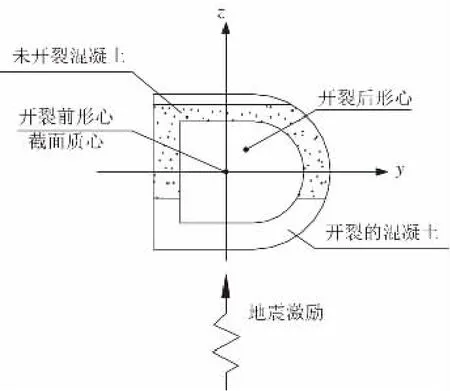
圖7 z向地震激勵引起形心偏移示意圖

如圖8所示，給橋墩施加y方向的地震激勵時，則開裂后有效截面的的形心僅產生一個方向的偏移，不會產生垂直于激勵方向的偏移，橋墩動軸力沒有產生垂直于激勵方向的附加彎矩，宏觀表現為沒有出現“雙彎曲”的現象。

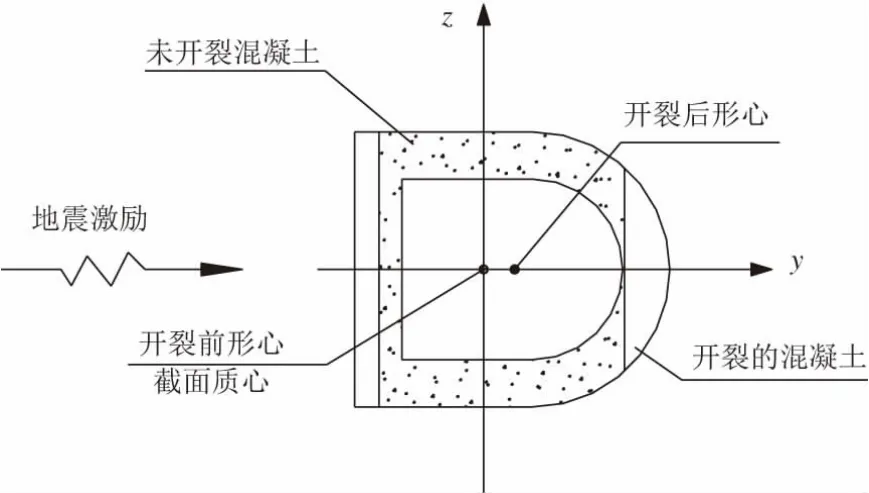
圖8 y向地震激勵引起形心偏移示意圖

如圖9所示，為了驗證以上推測，在OpenSees模型中將混凝土材料本構模型修改為線彈性進行線彈性分析，即不考慮混凝土的開裂作用，并在z方向施加地震激勵重新計算，得到墩頂位移時程曲線。

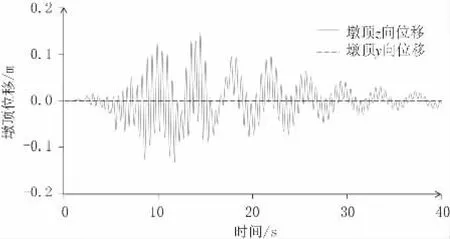
圖9 z向地震輸入墩頂彈性位移圖（單位：m）

由圖9可知，如不考慮混凝土的開裂作用，則在z方向地震激勵作用下，墩柱不再出現“雙彎曲”現象，進一步驗證了“雙彎曲”現象是由于混凝土不對稱開裂后導致有效截面形心產生垂直方向偏移所造成。

綜上所述，雙彎曲現象是由于當截面主軸關于激勵方向不對稱時，混凝土的不對稱開裂導致截面形心在垂直于激勵方向產生偏移，從而使得軸向力產生了垂直于激勵方向的附加彎矩所致，如混凝土不發生開裂則無雙彎曲現象。

2.3 P GA對“雙彎曲”的影響

為研究PGA對“雙彎曲”現象的影響，定義式（4）所示的雙彎曲系數：

式中：Dy，max為墩頂在平行于截面對稱軸方向的最大位移；Dz，max為墩頂在垂直于截面對稱軸方向的最大位移。雙彎曲系數η為兩個方向最大位移絕對值的比值。

如圖10所示，在垂直于橋墩截面對稱軸的z方向輸入地震激勵，并不斷增加輸入的PGA，得到雙彎曲系數變化曲線。

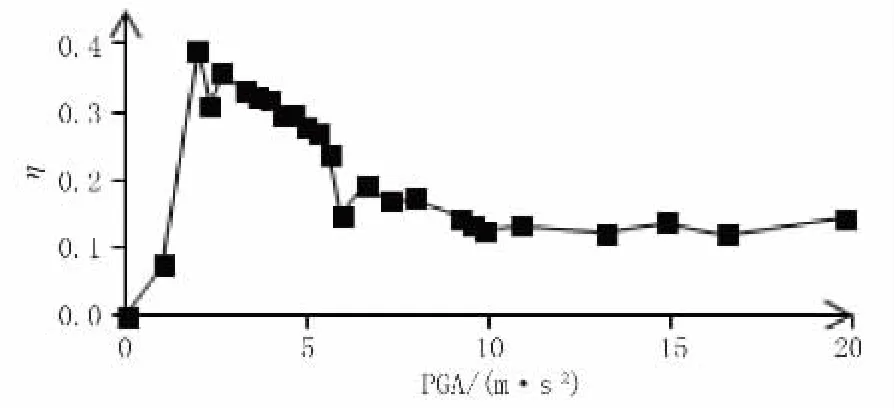
圖10 z向地震輸入雙彎曲系數-P GA曲線圖

由圖10可知，雙彎曲系數隨著PGA的增加先增加后降低，PGA達到一定數值后雙彎曲系數趨向于平穩不再減小，雙彎曲系數最大值約為0.4。推測造成這一現象的原因可能為一開始隨著PGA的增加，截面開裂程度加劇，導致有效截面形心相對于質心的偏移不斷增加，垂直激勵方向的附加彎矩不斷增加，雙彎曲系數逐漸增加；當PGA增加到一定程度后，截面已經充分開裂，此時有效截面僅剩截面腹板部分局部區域，有效截面形心相對于質心的偏移反而減小，從而使得雙彎曲系數降低。

3 結 語

（1）對于單軸對稱截面的橋墩，當沿著垂直于對稱軸方向施加地震激勵時，除在激勵方向會產生地震響應外，還會在垂直激勵方向產生地震響應，即出現“雙彎曲”現象。

（2）“雙彎曲”現象是由于橋墩截面的混凝土不對稱開裂，使得有效截面的形心相對于質心在垂直于激勵方向產生偏移，從而使得動軸力在垂直于激勵方向產生附加彎矩所導致。如沿橋墩對稱軸方向施加地震激勵，則不會出現“雙彎曲”現象。

（3）對于單軸對稱截面的橋墩，在垂直于對稱軸地震激勵作用下，其雙彎曲系數隨著PGA的增加后降低，當PGA達到某個值之后，雙彎曲系數不再有過大的變化，趨向于一個穩定值。

（4）目前現行設計規范[7-8]尚未對異形橋墩，尤其是單軸對稱截面的橋墩在單向地震作用下，垂直于地震方向產生附加彎矩提出相關設計方法，建議在該類橋墩的設計過程中應進行考慮。