平方耦合光力系統中光傳輸研究

于 凱 賈 曉

（南陽理工學院信息工程學院，河南 南陽 473004）

0 引言

近年來，通過調整光與1個或多個機械振子的相互作用來控制光的傳播的研究取得了許多成果。一種類似于原子物理學中電磁感應透明現象[1]，即光力誘導透明[2]，這一現象在最近的理論和試驗上都得到了證實。在最近幾十年的研究中，有關于光和機械振子耦合的研究大多數都是線性耦合的[3]。除了經典線性耦合的光力系統外，還存在一個平方耦合的光力系統[4]，即光腔場與機械振子位移的平方相互耦合。與線性耦合不同，平方耦合是雙聲子過程，而線性耦合只涉及單聲子過程，這使平方耦合能提供更多復雜的非線性效應。Huang和Agarwal分析了在平方耦合膜系統中也會出現的光力誘導透明效應，并解釋了環境溫度及其他系統參數影響平方耦合光力系統中出現透明窗口[5]的原因。平方耦合腔光力系統表現出復雜的干涉效應，導致信號場從不透明傳輸到透明再到被顯著放大[6]。這些現象取決于光力耦合的強度、弱相干驅動場的振幅和外加場的相位。因此，平方耦合的光機械系統可以用作光學晶體管，其中信號場可以被視為由控制場和探測場控制。首次觀察到電磁誘導透明現象是在原子蒸氣中，最近在量子阱、超材料等各種固體系統中也觀察到了電磁誘導透明現象。對腔光力學系統來說，在光學領域和微波領域都已經觀察到基于光力誘導透明的慢光與快光現象。

1 系統結構模型與動力學方程

1.1 物理結構

平方耦合光力系統原理圖如圖1所示。由1個振幅為εS、頻率為ωS的強探測場和1個振幅為εc、頻率為ωc的弱探測場共同驅動。機械諧振器的位置用x表示，l是法布里-珀羅腔的長度，kL=ηLk（kR=ηRK）表示左（右）鏡的空腔衰減率（K為總衰減率）。其中，總損耗率k=kL+kR+k0，k0表示系統固有損耗率，kL和kR分別表示左邊和右邊鏡子的耗散率，耦合參數ηL（ηR）可連續調節，選擇ηL=ηR=0.499。強控制場振幅為εS、頻率為ωS，弱探測場振幅為εc、頻率為ωc，力學驅動振幅為εd、頻率為ωd，εt-out表示輸出場振幅。

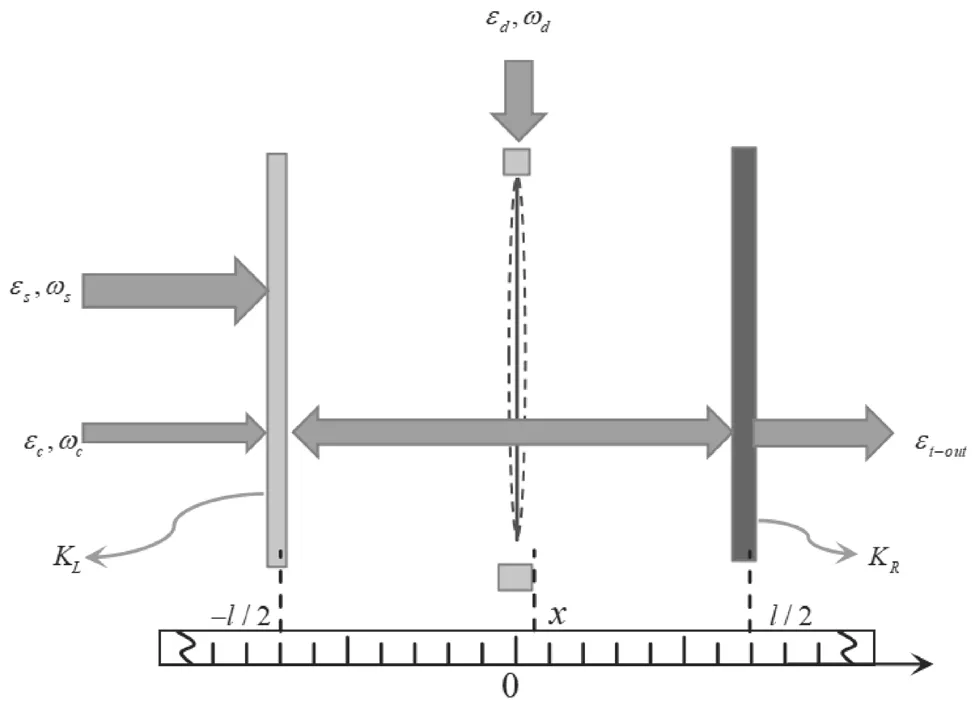
圖1 平方耦合光力系統原理圖

1.2 動力學方程

該平方耦合光力系統的哈總密頓量如公式（1）所示。

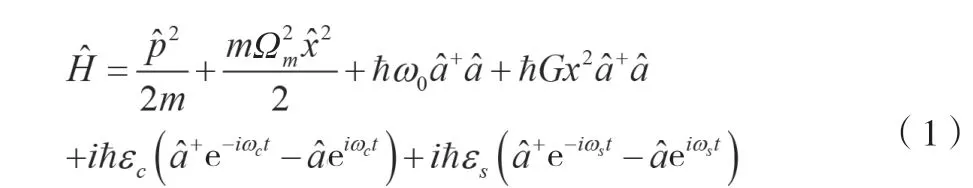
式中：δa為湮滅算符的波動值；δp為系統動量的波動值；δP為動量平方的波動值；A1+為湮滅算符一階上邊帶系數；A1-為湮滅算符一階下邊帶系數；A2+為湮滅算符二階上邊帶系數；A2-為湮滅算符二階下邊帶系數；x1為位移一階上邊帶系數；x1*為位移一階下邊帶系數；x2為位移二階上邊帶系數；x2*位移二階下邊帶系數；p1為動量一階上邊帶系數；p1*動量一階下邊帶系數；p2為動量二階上邊帶系數；p2*為動量二階下邊帶系數；X1為位移平方的一階上邊帶系數；X1*為位移平方的一階下邊帶系數；X2為位移平方的二階上邊帶系數；X2*為位移平方的二階下邊帶系數；P1為動量平方的一階上邊帶系數；P1*為動量平方的一階下邊帶系數；P2為動量平方的二階上邊帶系數；P2*為動量平方的二階下邊帶系數；Q1為動量平方的一階上邊帶系數；Q1*為動量平方的一階下邊帶系數；Q2為動量與位移乘積的二階上邊帶系數；Q2*為動量與位移乘積的二階下邊帶系數。

基于系統的光力非線性，輸出場有一系列的頻率分量（ωc±nω）產生，整數n是邊帶的階數。A1±表示一階邊帶的系數，頻率為ωc±Ω。其中，一階上邊帶ωc+Ω被稱為反斯托克斯場，一階下邊帶ωc-Ω被稱為斯托克斯場。該文只關注一階邊帶和二階邊帶的過程，忽略其他頻率分量。

該文重點討論輸出場的分量，它通過法布里-珀羅腔的右鏡傳輸，并在信號場的頻率上振蕩。利用輸入和輸出理論，可以得到法布里-珀羅腔傳輸的輸出場如公式（9）所示。

公式（10）表示信號和耦合場的貢獻，它在平方耦合光力系統中引起光機械誘導的不透明度。結果表明，信號場探測法布里-珀羅腔有3條途徑：通過右鏡直接透過光耦；通過2個聲子過程干擾磁共振散射的耦合場；通過2個聲子過程干擾磁共振直接機械驅動散射的聲子散射的耦合場。因此，信號場的透射譜是由這3條路徑的干涉決定的。其中，耦合功率Pc、相位差φ和機械驅動場的振幅εd發揮了重要的作用。

2 系統參數對系統透射譜線的影響

2.1 不同功率激光場的驅動對探測場透射率的影響

該文選擇的所有參數都來自于最近的試驗。可以清楚地看到，在平方耦合機制下，探測場的透射率隨著失諧量的變化的譜線圖如圖2所示。探測場透射率是指將一束探測光入射到平方耦合腔光力系統后，透過該系統的探測光的光通量與入射探測光的光通量的比值。失諧量為控制場與探測場之間頻率的差值。

圖2中|tp|2表示探測光的透射率，Ω=ωs-ωc是信號和耦合場之間的失諧量，Ωm=2 π×0.1 MHz為振子頻率，驅動功率為50 μW。

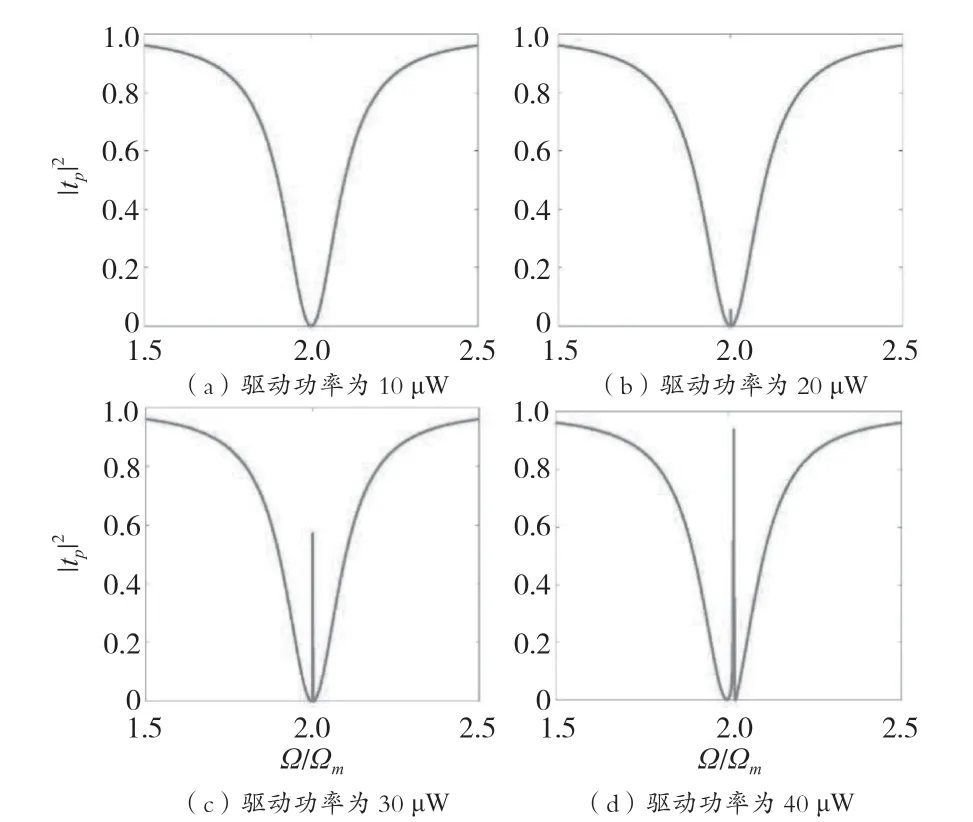
圖2 平方耦合機制下，探測場的透射率隨著失諧量的變化圖

圖2（a）在平方耦合機制下，受驅動場影響的探測場透射率隨著失諧量的增加不斷變化，在失諧量Δ=2 Ω時，控制場產生的反斯托克斯光與探測光發生干涉形成共振。圖2（b）增大驅動場的幅值，在該驅動場的影響下，在失諧量Δ=2 Ω時，探測場透射率發生變化，出現了1個很小的透明窗口。出現透明窗口的原因為探測場與驅動場2個頻率不同的激光形成1個拍頻，拍頻驅動振子，在該過程中出現非線性的上下轉換，產生反斯托克斯光，一階邊帶需要轉換1次，二階邊帶需要轉換2次，控制場失去2個振子，吸收或增加1個振子為反斯托克斯光。反斯托克斯場與探測場之間是共振的，反斯托克斯場與探測場的頻率相同，在腔場內方向一致，相位差恒定。即反斯托克斯場與探測場會發生相消干涉，從而使探測場的透射譜線在控制場與探測場失諧量和機械振子頻率匹配處出現1個透明窗口。圖2（c）繼續增大驅動場的幅值，在該驅動場的影響下，當失諧量為1.5 Ω～2.0 Ω時，探測場透射率逐漸減少，而當失諧量為2.0 Ω～2.5 Ω時，探測場透視率逐漸增大。當失諧量為Δ=2 Ω時，探測場透射率發生突變，此時，探測場透射率等于0.6，出現很明顯的透明窗口。圖2（d）繼續增大驅動場的幅值，在該驅動場的影響下，在失諧量為1.5 Ω～2.0 Ω時，探測場透射率逐漸減少，在失諧量2.0 Ω～2.5 Ω時，探測場透視率逐漸增大。在失諧量Δ=2Ω時，探測場透射率發生突變，此時探測場透射率趨近于1，即探測光被完全吸收。由于圖2中驅動場幅值的不同，因此會導致透射率譜線出現很大差異。其中，透明窗口出現的物理過程為控制場產生的反斯托克斯光與探測光發生相消干涉，使探測場的透射譜線在控制場與探測場失諧量和機械振子頻率匹配處出現1個透明窗口。而驅動場的功率大小會影響反斯托克斯場的出現，不能使所有的探測光都與反斯托克斯場發生相消干涉，影響透明窗口的出現。

2.2 溫度對透明窗口的影響

透明窗口（光力誘導透明現象）可以由泵浦光與探測光之間的拍頻Ω=ωp-ωl振蕩的輻射壓力來解釋，透明窗口出現的原因為如果驅動力接近于機械共振頻率Ωm，則振動模相干激發，導致強控制場光產生斯托克斯散射和反斯托克斯散射。如果在腔的紅邊帶驅動光學腔，腔場內的斯托克斯的散射過程將被抑制，只剩下反斯托克斯散射。當探測光與腔發生諧振時，控制場產生的反斯托克斯場與探測場之間是共振的，它們之間滿足干涉的條件，反斯托克斯場與探測場的頻率相同，在腔場內方向一致，相位差恒定。即反斯托克斯場與探測場會在法布里-珀羅腔內發生干涉，并導致出現透明窗口。

改變環境的溫度，選取T=50 K。將圖3的透射率譜線圖與圖2進行對比，升高溫度，透明窗口會變寬，出現了本征模式劈裂，透射率譜線從尖銳變得圓滑。如果繼續升高溫度，那么譜線會出現2次吸收凹陷，此時透明窗口消失。通過分析透射率譜線圖可以得出，溫度的變化很大程度地影響了透明窗口的大小，當溫度過大時會導致透明窗口消失。

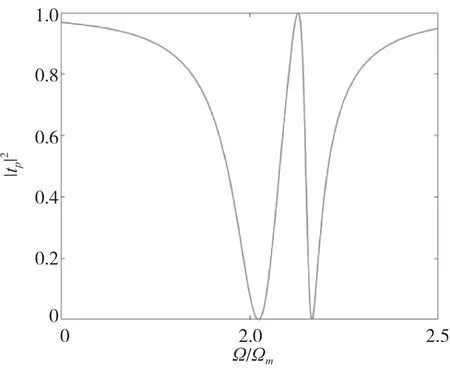
圖3 T=50 K時，失諧量對透射率的影響

3 結論

綜上所述，該文介紹了腔力光學的研究歷史、當前研究現狀以及非線性的平方耦合光力系統的模型，通過分析該模型，在雙色激光場包括控制場和探測場驅動在內的情況下，根據量子光學的基本知識寫出系統的哈密頓量以及其相應的海森堡-朗之萬運動方程。當控制場的強度遠遠大于探測場的強度時，即在微擾機制的條件下時，可以將系統運動方程中的光力非線性項線性化。在半經典近似的條件下，將運動方程中的算符寫為平均值和小量漲落的和，并忽略其高階小量，只保留到一階小量，從而得到線性化的運動方程。根據該線性化的運動方程可以求解一階邊帶即探測場振幅的解析表達式。最后通過MATLAB對理論計算的結果進行數值模擬并畫圖，進一步探究系統參數對探測場透射率的影響。該文主要探究了不同功率激光場的驅動對探測場透射率的影響以及溫度對透明窗口的影響。

驅動場功率的大小會影響斯托克斯散射，從而使腔場內反斯托克斯場與探測場發生不完全的相消干涉，影響透明窗口的出現。溫度也會影響透明窗口的大小，當溫度過大時，會出現本征模式劈裂，從而導致透明窗口消失。