基于合作博弈的個人綜合所得稅地區分配方式研究

一、引 言

個人綜合所得由個人的工資薪金、勞務報酬、稿酬和特許權使用費所得四項所得構成。從2019年開始，綜合所得的稅收按年征收，納稅人在第二年將上一年度全部綜合所得進行費用扣除、專項扣除、專項附加扣除、合理的捐贈扣除和法律規定的其他扣除后，將應納稅所得對應綜合所得的七級累進稅率向稅務部門進行申報納稅和匯算清繳。綜合所得征稅的方式，使納稅人來自不同地區的綜合所得統一納稅，改變了以往分類所得在來源地納稅的方式。個人所得稅的征管方式，從分類所得的代扣代繳轉變為預扣預繳和申報匯算清繳的方式。具有多處綜合所得來源的個人，需要向主管稅務機關申報納稅進行匯算清繳：如果預扣預繳的稅額比應納稅額少，個人需要補稅；反之，如果預扣預繳的稅額比應納稅額多，主管稅務部門要對納稅人進行退稅。由于個人收入來源于多處地區，相比原來分類所得征收，綜合征收產生了稅務部門退稅分攤和稅收地區間分配的兩個新問題：

首先是主管部門對納稅人的退稅如何在不同收入來源地分攤的問題。納稅人由于工作地點變動、收入的地區分布差異等原因導致納稅申報主管稅務地和主要收入來源地不一致，負責納稅人辦理匯算清繳退稅的地區可能并沒有獲得納稅人預扣預繳的稅收。法律規定由主管稅務部門先行辦理退稅，但是退稅和預扣預繳的差異會影響地區之間稅收收入的分布。這導致了匯算清繳主管地和個人收入來源地的稅收利益沖突。

痊愈為NIHSS評分減少≥90%，腦電圖正常；顯效為90%＞NIHSS評分減少≥50%，腦電圖顯著改善；有效為49%＞NIHSS分恢復≥15%，腦電圖有所好轉；無效為以上指標均未滿足。

其次是各收入來源地如何分享個人的稅收。在分類征收時，個人在每個地區獲得收入時代扣代繳的稅收直接歸屬于收入來源地，各地的收入彼此無關，收入來源地可以獲得相應的稅收。在綜合所得稅制下，在收入來源地只是預扣預繳，所有地區一年內的綜合所得合并在一起計算納稅人的最后應納稅額。由于累進稅率和共享納稅人的扣除，各地的收入互相影響，共同決定納稅人的綜合所得應納稅額。預扣預繳的稅率和納稅人綜合所得的最后適用稅率并不一致，如果納稅人年度匯算申報時補稅，需要解決相應稅收如何根據個人來自各地的綜合所得進行分配的問題。

對這兩個問題，當前的解決方法是由匯算清繳地負擔全部退稅，也由匯算清繳地獲得全部匯算清繳時補繳的稅收。當前分配方案下，預扣預繳地區獲得預扣預繳的稅收，而匯算清繳地區獲得全部收入的稅收，并對其他地區已經預扣預繳的稅收提供可退稅的抵免。這使得匯算清繳地所得適用個人綜合所得稅率，而其他地區的所得只適用預扣預繳稅率。當個人全年綜合所得最高邊際稅率低于其他地區預扣預繳的稅率時，匯算清繳地負責退稅，就產生了預扣預繳地和匯算清繳地之間的稅負輸出問題。因而，現行分配方案沒有考慮各地收入在稅收創造中的公平地位，存在來源不同地區所得適用稅率差異和地區間稅負輸出問題。

退稅分攤問題和地區稅收分配問題可以分別單獨解決，也可以同時一起解決。如果確定了個人綜合所得稅在地區之間分配的方式，退稅分攤的問題可以看作是地區稅收分配的子問題，兩個問題按照統一的方式進行解決。本文從合作博弈解的分配角度，提出了基于原則的地區之間個人綜合所得稅的分配方式，為完善綜合所得稅制提出了解決和改進思路。

雖然個人所得稅地區間分配問題剛剛出現，規模和人數都在初步階段，但是隨著直接稅在我國稅收收入比重的上升，本文研究的意義會日漸重要。在營改增完成之后，個人所得稅已經成為地方政府財政收入的重要來源，如何分配個人所得稅收入對地方提供公共服務能力具有重要影響。個人所得稅已經是我國稅收收入中重要的稅種，2018年在全國稅收收入中占第3位，在地方稅收收入中占第5位。個人所得稅是中央和地方分享稅，中央和地方按照60比40分享當地的稅收收入。在分類征收時，來自各地區的收入由地方和中央直接交涉，各地區之間互不干涉。但在綜合所得征收后，納稅人來自各地的綜合所得共同決定最后應納稅額。個人綜合所得稅地區分配問題，涉及到財稅體制的地區稅收分享問題，是我國建設現代財稅治理體制的重要問題。

第四，配套完整、齊全的法律法規。目前面臨的實際情況是，對于重組整合，相應的法律法規條款不完善。某些具體的條款不夠全面完整。對于某些情況取而代之的是行政指揮命令的方式。這種也很容易影響權利尋租，金錢交易等情況。進而阻礙企業的重組整合進度。影響進度和效率。

在購置實驗教學儀器設備之前，應該有詳細的購置計劃，盡量避免購買重復的實驗器材，合理地利用實驗建設經費，在列采購清單前一定進行以下幾項：首先，查看現有的實驗設備是否滿足實驗需求，其次，統計實驗室提出的設備購置申請，最后請專家按照教學大綱合理地對采購清單進行審核修改，交到財務部門進行審核，審核通過后給予采購。

在我國的稅制發展過程中，其他稅種也有涉及類似的地區之間稅收分配問題。但是以下三個個人所得稅的特征決定了政府需要根據個人所得稅的特點制定新的辦法：

用不同濃度的 GSK126 （0、2、5、10、15、20、30、40、50、80 μmol/L） 干預 ONFH 組 MSCs，以確定GSK126最適濃度。然后以最適濃度干預細胞，觀察24、48、72 h后細胞增殖情況。調整細胞懸液濃度為2×104/ml，接種于96孔板，各組10孔。培養一定時間后，每孔加入MTT溶液20 μl，37℃孵育4 h后去除上清液，每孔加入150 μl DMSO，振蕩10 min，酶聯免疫檢測儀測定各孔吸光值（波長490 nm）。

第一，個人所得稅納稅人數規模大。增值稅和企業所得稅主要涉及企業行為，而個人所得稅涉及個人。根據公開報道，個人所得稅的納稅人有2.5億人

，需要納稅申報的人數規模可能達到8000萬

。根據第四次全國經濟普查公報，2018年末全國共有從事第二產業和第三產業活動的法人單位2178.9萬個

。個人納稅人的數量超過了企業納稅人。

值分配作為合作博弈的解最早由Tijs(1981)提出

。在一個合作博弈(

,

)中，

=

(

)-

(

{

})是地區

在博弈中能得到的收益的支付上限，如果地區

的收益高于這個上限，其他

-1個地區就不愿意和地區

組成聯盟來分配收益。因而

維向量

=(

,

,…,

)稱為博弈的理想值向量。在綜合所得稅地區分配中，

表示參與人地區在形成聯盟時在最后一個加入聯盟的邊際收益。由于綜合所得稅地區分配博弈是凸博弈，對于任意

?

?

{

}，都有

(

∪{

})-

(

)≤

(

∪{

})-

(

)。在形成大聯盟的過程中，最后一個加入的邊際收益大于其他位置加入時的邊際收益

。由于累進稅率，這是地區

的綜合所得可以適用個人可以達到的最高邊際稅率時帶來的稅收增加。對于任意地區

和任意包含

的聯盟

，如果其他每個參與人都得到理想值支付，形成聯盟后的價值對于參與人

的剩余值為：

第三，個人收入明確。個人因任職、受雇、提供勞務、創作或者轉讓特許權獲得所得，通常是市場公平交易。而企業總分機構之間的交易存在內部轉讓定價，因而個體的收入具有客觀公平性，預扣預繳稅務部門具有可靠的記錄，可以作為分配稅收的基礎。

個人所得稅的納稅人數目規模大、地區流動頻繁和收入明確的特點，使得通過固定公式根據納稅人來自各地的綜合所得在地區之間進行公平合理分配，具有公平、公開和公正的特點。通過固定公式分配，分配方式在地區之間透明，便于各地區合作，維護各地區的稅收利益。在納稅遵從方面，也便于納稅人理解執行，不影響納稅人就業選擇和納稅遵從。聶海峰和劉怡(2020)建立了一個合作博弈模型，討論了博弈的Shapley值作為地區間稅收分配辦法的性質，將地區間稅收分配問題轉化成了文獻中的破產問題，提出應用比例法在地區間分配稅收：各地區根據來自當地的綜合所得占納稅人全部綜合所得的比例來分享納稅人應納稅額

。但是比例法分配沒有考慮到各地區的收入在納稅人稅收創造過程中的作用。

合作博弈是描述多個參與人之間存在約束性協議時，如何在參與人之間公平合理分配彼此共同合作的收益的理論

。在個人綜合所得稅地區分配問題方面，收入來源的各地區彼此間存在合作和沖突，正好適應合作博弈分析的情景：每個地區都對來自當地的收入有稅收征管權，綜合所得的累進稅率使得個人的收入越多時適用的稅率越高。稅收分配要保證各地對來自當地稅收的基本權利，也要保證分享所有地區一起合作的收益。一旦中央政府選定分配方式，參與地區存在執行協議的約束性。作為地區間稅收分配方式，至少滿足三個性質：首先是效率性，即所有地區分配相應的全部稅收，并且各地區之間不能存在交叉補貼；第二是對稱性，即兩個具有相同收入的地區應當分配相同的收入；第三是單調性，即綜合所得多的地區分配的稅收應當不低于綜合所得少的地區分配的稅收。合作博弈的多種解都滿足上述三個性質。

本文的貢獻是考慮了合作博弈的多種解，豐富了個人所得稅地區間分配問題的解決方案。和Shapley值一樣，核仁(Nucleolus)和

值作為合作博弈的解也滿足效率性、對稱性和單調性的性質。在合作博弈中，對于“公平”的不同解釋導致不同的合理解。在Shapley值分配中，每個參與人得到了在合作中的邊際貢獻。核仁反映了分配方案中不同地區組合的所得和他們自身可以創造稅收的差異的最小化，是福利經濟學中羅爾斯原則——最大化境遇最差人福利的應用。

值反映參與人在合作博弈中理想值和最小權利值之間的折中。最小權利值反映了參與人參與博弈時至少應當獲得的最低收益，而理想值是他參與合作時能獲得的最大可能收益。

值分配中，每個參與人保證獲得他的最小權利值之后，剩余的合作收益按照每個人未滿足的理想值成比例分配。

(1a)趙先生在兩處任職受雇地獲得工薪收入，趙先生選擇A地為主管稅務機關所在地。因此，趙先生的專項附加扣除在A地每月工薪所得領取時使用。因而在A地，趙先生的工薪應納稅所得為

=4*12=48萬元。由于費用扣除=0

5*12=6萬元，專項扣除=1*12=12萬元，專項附加扣除=2

4+2

4=4

8萬元，趙先生在A地預扣預繳時的全年應納稅所得=48-6-4

8-12=25

2萬元。在A地被全年累計預扣預繳的稅款為

=0

2*25

2-1

692=3

348萬元。

合作博弈的解作為公平合理的分配方式，已經被廣泛應用：比如美國田納西流域建設成本分攤方法和合作博弈中各種解的關系

，合作博弈在保險研究中的應用

，以及合作博弈在中國機場起降費規制改革中的應用

。鑒于Curiel、Maschler和Tijs(1987)提出在破產博弈中利用

值解決破產后債務清償問題

，本文嘗試將

值分配用于解決地區個人所得稅的分配問題。

本文余下內容安排如下：第二部分首先對地區稅收分配問題構建合作博弈模型，第三部分介紹核仁和

值的性質，將其與Shapley值分配進行對比，并用案例比較分配結果。最后是全文的總結，討論影響個人所得稅地區間分配方法選擇的因素。

早在2008 年西門子公司因違反《反海外腐敗法》被處罰金16 億美元，成為全球企業合規發展的一個里程碑事件。從那以后，強化合規管理、防范合規風險已經成為越來越多企業管理創新的重要內容。統計數據顯示，自2014 年初以來，已公開宣布115 名國有集團公司的決策層高管因貪污而受到調查，一些央企的主要負責人被調查或處罰。

二、個人綜合所得稅地區分配問題

(一)個人綜合所得稅匯算清繳

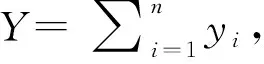
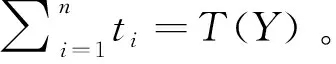
(二)合作博弈分析

合作博弈和傳統的非合作博弈不同。合作博弈關注合作利益分配方式的研究，而非合作博弈關注參與人的利益最大化的均衡策略的確定。非合作博弈關注自利參與人的選擇的激勵相容性，而合作博弈關注收益分配方法的公平、效率和個人理性。

從合作博弈角度，個人綜合所得稅地區分配問題對應著

個地區之間合作利益分配問題。Von Neumann和Morgenstern(1953)最早提出了聯盟形式的合作博弈

。帶轉移效用的合作博弈由二元組(

,

)表示，這里

={1,2,…,

}表示參與人集合，

是從集合

的所有子集到實數集合的映射，

:2

→

。對于任意參與者的聯盟

?

,

(

)給出該聯盟合作的價值。在稅收地區分配問題中，參與人是個人獲得綜合所得的地區，

(

)=

(∑

∈

)等于所有聯盟

中的地區聯合起來可以從該個體獲得的稅收收入。當個人收入來源于多個地區時，地區之間的信息共享才能使得在個人申報納稅時實現綜合所得稅的良好征管。

(∑

∈

)反映了聯盟地區之間信息共享、聯盟外的收入信息不被聯盟分享的極端假設。對于空集?，有

(?)=0。

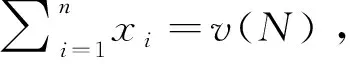
確定合作博弈的解就是尋找恰當分配方案，將合作的收益在參與人之間分配。常用的一個分配原則是激勵原則：由于各個成員之間可以組成聯盟，每個聯盟分配的總和不應當低于他們自身組成聯盟時的收益。否則，聯盟成員就沒有參加大聯盟收益分配的激勵。這意味著對于任意的聯盟

，都要有∑

∈

≥

(

)。滿足激勵原則的分配方案稱為博弈的核心(

)。

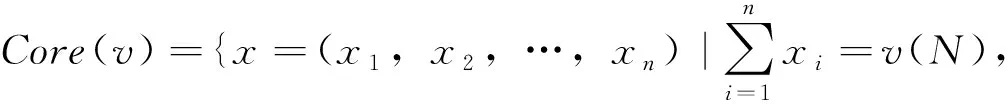
對于凸博弈，核心總是存在但不唯一，因而不能給出單一值的合理分配方案。在文獻中，廣為使用的單一值分配方案是Shapley值、核仁和τ值。作為合作博弈的解概念，可以給出可行的合理分配方案。

三、地區稅收分配合作博弈的解比較

(一)Shapley值分配

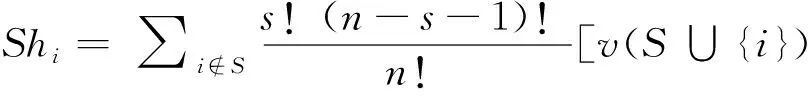
(二)核仁分配

在第二年3月1日至6月30日內，趙先生由于從兩處以上取得綜合所得，且綜合所得年收入額減除專項扣除后的余額超過6萬元，趙先生到主管稅務機關A地的稅務部門辦理個人申報進行個人匯算清繳。

2.2 兩組患者冠狀動脈造影、介入治療及術后情況比較 兩組患者冠狀動脈造影結果提示“罪犯”血管累及回旋支和右冠的比例、術前TIMI血流、術后嚴重出血、急性／亞急性支架內血栓形成、延遲支架植入比例等方面差異無統計學意義（P＞0.05）；兩組“罪犯”血管累及左主干和前降支的比例、＞70%狹窄的冠脈病變數、術中發生無復流、冠脈支架術后TIMI血流和完全血運重建的比例等方面，差異有統計學意義（P＜0.05）。見表2。

(三)τ值分配

第二，個人流動性高于企業。企業登記注冊和經營地相對固定，企業的遷移成本較高。隨著戶籍制度完善，教育、就業以及醫療、養老、住房保障等領域的配套政策加快完善，人口就業地區之間流動的頻率和規模遠遠高于企業。根據《中國流動人口發展報告2018》推算，2017年全國流動人口總量為2.445億人。

(

,

)=

(

)-∑

∈{}

(1)

參與人

的最小權利值(Minimal Right Value)定義為

=max

;∈

(

,

)，表示參與人

可以通過形成一個聯盟，支付聯盟中其他參與人可以得到的上限支付后，確保自己得到的支付。如果地區之間可以自由結合成各種聯盟時，這是地區

可以確保得到的最小支付。因而

維向量

=(

,

,…,

)稱為合作博弈的下值向量。

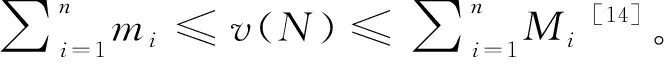
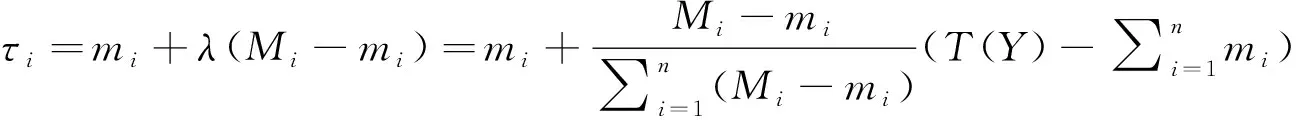
(2)

值作為博弈中參與人的理想值和下值的折中，也具有良好的性質。首先它滿足效率性，在所有參與人之間分配合作的總收益；其次滿足對稱性，如果兩個地區具有相同的綜合所得，

值會分配相同的稅收；再次滿足單調性，如果

≥

，則

≥

，即來自地區

的綜合所得大于來自地區

的綜合所得，那么分配給地區

的稅收不低于分配給地區

的稅收；最后，如果每個地區單獨的綜合所得的稅收為零(

=0)，那么所有地區分配的稅收和他們的理想值

成比例。因而，

值的分配類似一種調整比例分配辦法，先分配給每個地區的下值對應的稅收，然后將未分配的稅收，根據去掉已經分配的稅收后的理想值稅收按照比例進行分配。當成比例分配時，

值分配是根據理想稅收收入的比例分配的，而不是根據該地區的綜合所得進行分配，更好反映了收入創造稅收的功能。

重組改構人腫瘤壞死因子對比順鉑胸腔灌注治療惡性胸腔積液療效與安全性的系統評價 ……………… 郭奇遇等（6）：839

(四)三種分配方案比較

Shapley值、核仁和

值分配都滿足效率性、對稱性和單調性的性質。這三種分配結果有時相同，但是相對來說，

值的計算步驟最簡單，而Shapley值分配和核仁分配的計算過程都比較復雜。

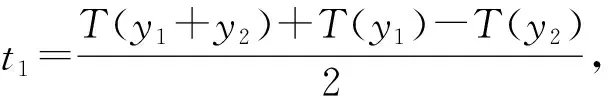
1.3.1 小鼠LLC細胞培養及肺癌移植瘤模型建立 收集對數生長期LLC細胞，制成1×106個/mL的單細胞懸液；0.2 mL/只，皮下注射入30只C57/BL6小鼠左側腋下，觀察、記錄LLC小鼠生長及成瘤情況。

對于一般的情形，這三種分配方法分配的結果不同。Shapley值分配和核仁分配結果總是在博弈的核心中。如果參與分配的地區超過4個，

值的分配可能不在博弈的核心中

。雖然在給定收入時，Shapley值分配和核仁分配都滿足單調性，但是核仁分配不滿足聯盟單調性(Coalition Monotonicity)和強單調性(Strong Monotonicity)。聯盟單調性是指兩個聯盟博弈(

,

)和(

,

)，存在一個聯盟

滿足

(

)>

(

)，但是對于任意

≠

，都有

(

)=

(

)，那么對于任意

∈

,

(

,

)

>

(

,

)

。這里

是博弈的解，表示如果博弈中某個聯盟的收益增加了而其他聯盟收益不變，那么這個聯盟中包含的參與人分配的收益也要增加。強單調性是指如果對于任意

,

∈

,都有

(

)>

(

)，那么

(

,

)

>

(

,

)

。強單調性意味著如果包含參與人

的所有聯盟的收益增加了，那么參與人

分配的收益也要增加。Megiddo(1974)通過構造例子表明核仁分配不滿足聯盟單調性，因而也不滿足強單調性

。在地區稅收分配中，分配方案滿足強單調性意味著如果其他地區的綜合所得不變，來自一個地區的綜合所得增加了，那么這個地區在收入增加后分配稅收不低于收入增加前分配得到的稅收。由于核仁分配不滿足強單調性，這對核仁的應用是一個不利之處。

在計算復雜性方面，

值的計算最為簡單，只需要計算2

+1個聯盟的收益；而Shapley值分配和核仁分配都需要計算所有2

個聯盟的收益，計算的工作量較大。因而，從計算簡單性角度考慮，

值分配方法也是一種具有良好應用前景的選擇。

楊宗祥曾經說過“企業家應以人為本來管理企業，董事長及高管、班組長不可能天天去當操作工、開挖機，這些行業的員工很辛苦，企業家要將心比心，解決員工后顧之憂，企業才能獲得長遠的發展”。為員工購買社會保險，遭遇金融危機工資不降，開發物業成本價基礎上還發放補助金保證職工有房住，員工的工會活動經費總是第一時間達到，外加中午免費的午餐。公司各項福利水準在安寧當地也算上乘，絕大多數員工能安心本職工作，公司還為職工新建500套經濟適用房，3000多名職工安心本職作業，多年來企業人員流失率始終保持在5%以下。

(五)案例分析

這里考慮一個收入來源于多地的地區稅收分配案例。趙先生有2個子女，都在中小學讀書，妻子未工作。他沒有再接受繼續教育，首套住房的貸款已經結清。趙先生為獨子，父母雙方健在，都超過了60歲。家人都健康，未有疾病。因而，在6項個稅專項附加扣除方面，趙先生只適用子女教育和贍養老人兩項，其中子女教育2

4萬元

年，贍養老人2

4萬元

年。

(a)趙先生在甲省A地任職，每月工資收入4萬元，三險一金個人部分需繳納1萬元。

(b)因工作關系，公司派趙先生兼任甲省B地公司經理，在該公司每月工資收入2萬元，三險一金個人部分繳納0

5萬元。

(c)趙先生6月被邀請赴乙省C地講學一周，當地主辦單位支付趙先生勞務報酬10萬元。

(d)趙先生10月的一部書稿被丙省D地出版社出版，出版方支付稿酬5

7142萬元。

(e)11月份，趙先生早年一部劇本的電影改編版權轉讓給丙省E地的一家影視公司，對方支付轉讓費6萬元。

1

代扣代繳階段

以上為趙先生全年收入，下面分別計算趙先生在各地取得收入時的代扣代繳情況和第二年個人申報納稅匯繳清算情況。

(1b)在B地，趙先生工薪應納稅所得

=2*12=24萬元，預扣預繳時費用扣除和專項扣除都為6萬元。在B地預扣預繳時全年應納稅所得=24-6-6=12萬元。在B地被全年累計預扣預繳的稅款為

=0

1*12-0

252=0

948萬元。

本文的另一個貢獻是提出了更具可行性的分配方式。相比于Shapley值和核仁分配，

值分配的計算公式較簡單，在實踐中更便于應用。

值也擴展了比例法。在比例法中，每個地區分配稅收與來自該地的綜合所得成比例；在

值分配中，每個地區保證了單獨的貢獻之后，分配的稅收和來自當地的綜合所得能創造的最大稅收成比例。

值分配可以看作是一種調整后的比例分配。與按照綜合所得比例法分配相比，

值考慮了各地區收入在稅收創造過程中的作用，分配的比例因素是每個地區未滿足的理想稅收收入。

海水中懸浮物顆粒對光的選擇性吸收是線性衰減系數不穩定的主要原因。在清澈的海域,除了藍光的吸收和散射對光的衰減基本相等外,其他顏色的光衰減基本上是因為海水的吸收。在懸浮物比較多的海域,光的衰減則大部分來源于光的散射。而光在傳播時產生的熒光散射和拉曼散射則包括了吸收和受激輻射兩個基本過程。一般情況下,吸收作用造成的光量的衰減約占光源的40%,而其大部分原因是來源于光的散射作用。

(1c)扣除20

的費用后，趙先生來自C地的勞務報酬收入額

=(1-0

2)*10=8萬元。在C地預扣預繳的稅款為

=0

4*8-0

7=2

5萬元。

干線公路項目施工過程中的質量安全風險管理問題探析………………………………………………………… 李梅（4-229）

(1d)來自D地的收入為稿酬所得，因而在D地的應納稅所得

=(1-0

2)*0

7*5

7142=3

2萬元。按照20

的比例預扣率，在D地預扣預繳的稅款為

=0

2*3

2=0

64萬元

(1e)來自E地的收入為特許權使用費所得，在E地的應納稅所得

=(1-0

2)*6=4

8萬元。按照20

的比例預扣率，在E地預扣預繳的稅款為

=0

2*4

8=0

96萬元

2.個人匯算清繳階段

核仁是由Schmeidler(1969)提出的合作博弈的分配解

。Shapley值分配側重考慮參與人在形成聯盟時的邊際貢獻，而核仁強調分配的公平性，可以看作是從公平角度最大化最小分配方案差異的結果。Inarra、Serrano和Shimomura(2019)是對核仁研究的最新全面綜述

。

趙先生的全年稅前收入=48+24+10+5.7142+6=93.7142萬元。費用扣除為6萬元，兩處取得工薪所得的專項扣除=12+6=18萬元，6項專項附加扣除=4.8萬元。扣除勞務報酬、稿酬所得和特許權使用費所得的費用后，趙先生綜合所得收入額Y=48+24+8+3.2+4.8=88萬元。因而，全年綜合所得應納稅所得=88-6-18-4.8=59.2萬元。根據對應的邊際稅率和速算扣除數，應納稅額T(Y)=0.3*59.2-5.292=12.468萬元。

趙先生被預扣預繳的稅收總額=3.348+0.948+2.5+0.64+0.96=8.396萬元。因而，趙先生需要向A地主管稅務機關補繳稅款12.468-8.396=4.072萬元。趙先生稅前收入的個人所得稅負擔率=12.468/93.7142*100%=13.3%。

3.綜合所得稅地區分配階段

趙先生全年綜合所得收入額88萬元來自5個地區，共享趙先生的費用扣除、專項扣除和專項附加扣除之后按照七級累進稅率表創造了12.468萬元的稅收。在地區之間的稅收分配，就是按照前文提到的合作博弈的分配方法分配趙先生的稅收。然后根據分配的稅收，其他4個地區和A地的主管稅務機關進行匯算清繳。表1中列出了按照Shapley值、核仁值和

值分配的地區稅收。相應分配的稅收和當地已經預扣預繳的稅收的差額就是與A地匯算清繳的數額。

從表1中列出的稅收分配方案可以看到，如果不進行稅收地區間分配，來自B地的收入高過了C地，但是預扣的稅收低于C地。在匯算清繳階段，補繳的稅收將都歸屬與A地。B地的稅收利益受到較大的影響。

一直以來，無論是市場營銷學理論界還是教科書，都把市場營銷分為傳統和現代兩大觀念，作為市場營銷學的經典理論被廣泛應用。

在不同分配方案中，來自A地的應納稅所得最高，A地分配的稅收也最多；來自D地的應納稅所得最低，相應分配的稅收就最少。三種分配方法中，Shapley值方法分配給A地6.83萬元，核仁方法分配給A地區6.638萬元，而

值方法分配給A地區6.768萬元。在給D地的稅收分配中，核仁方法分配了0.48萬元，Shapley值方法分配了0.464萬元，

值方法分配了0.469萬元。因而，Shapley值強調邊際貢獻，對來源應納稅所得最高的地區分配的稅收較大，而核仁方法對應納稅所得較小的地區分配的稅收相對Shapley值方法有所調整。

除了A地之外，其他四個地區的應納稅所得都小于個體的扣除合計，如果單獨計算應納稅收等于0，四個地區的τ值分配的稅收成比例。如果按照應納稅所得的比例分配，A地分配的稅收將是B地的2倍，但是按照

值分配時，A地分配的稅收高于B地的2倍，反映了在累進稅率下A地創造稅收的能力更高。因而，

值分配也優于按照應納稅所得比例分配。

四、總 結

個人綜合所得稅制是當前稅制改革的新生事物，跨地區個人所得稅分配也是一個新的現象。具有跨地區綜合所得的納稅人的數目，所得規模和相應稅收的規模都需要新的統計。因而，對于跨地區的個人所得稅退稅和地區分配問題，主管部門需要進行如下決策：第一，是否由主管稅務機關負擔所有退稅；第二，是否在地區之間分配個人跨地區所得個人綜合所得稅；第三，如果分配，采用哪種原則在地區之間分配個人綜合所得稅。對于前兩個問題，由于目前個人所得稅比例較低，綜合所得稅制剛剛建立，采用過渡的辦法，由主管稅務機關負擔所有退稅，不在地區之間分配跨地區個人綜合所得稅。但是，隨著全國勞動力市場統一，勞動力普遍自由流動，個人所得稅占稅收收入比重增加，跨地區所得成為普遍現象，維護地區間財政收益將成為重要的問題。本文分析討論的各種分配方法，對未來的政策設計提供了參考指導，幫助政府未雨綢繆，提前謀劃。

合作博弈的解對應的分配方法，為個人綜合所得稅在地區之間分配提供了選擇方案，保證了各地區的收入得到公平的對待，并且具有明確可以執行的公式，具有透明性的優點。本文比較了合作博弈中廣泛使用的Shapley值、核仁和

值三種博弈解對應的分配方案。這三種解給出的分配方式都滿足良好的性質：效率性、對稱性和單調性。但是核仁不滿足聯盟單調性，會導致來自一個地區的收入增加后分配的稅收減少的情況。因而，Shapley值和

值作為地區間分配綜合所得稅的可行方案具有良好的性質。當個人收入來源地區較多時，Shapley值計算量比較大，在實際應用中較復雜；而

值分配的計算公式簡單，結合了比例分配法的優點，具有容易使用和推廣的潛力。

當然，多元合作英譯模式僅是一種宏觀的指導思想，要想做好“花兒”外譯還需要提出具體的英譯策略與方法。“花兒”是一種典型的民間口頭傳承詩歌，與傳統詩歌有著極大的差異，不能簡單套用譯介傳統詩歌的方法，必須另辟蹊徑。對民俗學的口頭程式理論和表演理論進行跨學科的闡發，可為“花兒”的英譯研究提供新視角、新方法。

在具體實踐中，除了效率、公平、單調和簡明計算的特征之外，影響分配方法選擇的另一個因素是收入影響規模。本文的進一步研究方向，就是利用具體的稅收統計數據比較各種分配方法對地區之間稅收收入分布的影響。

[1] 聶海峰, 劉怡. 個人所得稅地區間匯算清繳方法研究[J]. 財政研究, 2020, (5): 90-102.

[2] Bezalel P., Sudh?lter P. Introduction to the Theory of Cooperative Games[M]. Berlin Heidelberg: Springer, 2007.

[3] Straffin P., Heaney J. P. Game Theory and the Tennessee Valley Authority[J]. International Journal of Game Theory, 1981, (1): 35-43.

[4] Lemaire J. Cooperative Game Theory and Its Insurance Applications[J]. Journal of the International Actuarial Association, 1991, 21(1): 17-40.

[5] 董保民, 郭桂霞. 機場博弈與中國起降費規制改革: 一個合作博弈論評價[J]. 經濟學(季刊), 2006, (3): 1235-1252.

[6] Curiel I., Maschler M., Tijs S. H. Bankruptcy Games[J]. Zeitschrift für Operations Research, 1987, (5): 143-159.

[7] Von Neumann J., Morgenstern O. Theory of Games and Economic Behavior[M]. Third Edition. New York: Princeton University Press, 1953.

[8] Shapley L. Cores of Convex Games[J]. International Journal of Game Theory, 1971, (1): 11-26.

[9] Shapley L. A Value for N-person Games[C]∥ Kuhn H. W., Tucker A. W. (Eds.). Contributions to the Theory of Games II. Princeton: Princeton University Press, 1953: 307-317.

[10] Schmeidler D. The Nucleolus of a Characteristic Function Game[J]. SIAM Journal on Applied Mathematics, 1969, (6): 1163-1170.

[11] Inarra E., Serrano R., Shimomura K. I. The Nucleolus, the Kernel, and the Bargaining Set: An Update[J]. Revue Economique, 2019, (2): 225-266.

[12] 譚春橋, 張強. 合作對策理論及應用[M]. 北京: 科學出版社, 2011.

[13] Tijs S. H. Bounds for the Core and the

-value[C]∥ Moeschlin O., Pallaschke D. (Eds.). Game Theory and Mathematical Economics. Cie: North-Holland Publishing Company. 1981: 123-132.

[14] Tijs S. H., Lipperts F. A. S. The Hypercube and the Core Cover of N-person Cooperative Games[J]. Cahiers du Centre d’études de Recherche Opérationnelle, 1982, (1): 27-37.

[15] Tijs S., Otten G. Compromise Values in Cooperative Game Theory[J]. Top, 1993, (1): 1-36.

[16] Megiddo N. On the Non-Monotonicity of the Bargaining Set, the Kernel, And the Nucleolus of a Game[J]. SIAM Journal on Applied Mathematics, 1974, (2): 355-358.