基于 App Designer 開發的傅科擺仿真模擬 ①

劉小琪, 吳 穎

(北京師范大學物理學系，北京 100000 )

0 引 言

法國物理學家傅科于1851年在巴黎萬圣殿內的拱頂上懸掛了一個擺長67m，擺錘質量為28kg的單擺，該單擺擺動周期約為16s，實驗發現該單擺平面繞豎直軸作順時針轉動(由上向下看)，轉動周期約為 32h，這就是著名的傅科擺實驗。傅科擺實驗無需依賴地球以外的物體，就能直觀地展示地球自轉的存在，是物理學史上最美麗的實驗之一。對傅科擺的仿真模擬研究具有重要的教學意義。

1 傅科擺的理論推導

1.1 考慮自轉的重力加速度

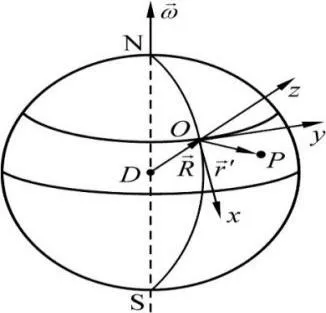
圖1 隨動坐標系建立示意圖

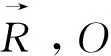
(1)

O 點加速度可以表示為

(2)

根據非慣性系中加速度的公式

(3)

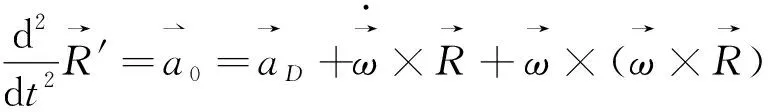
(4)

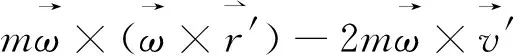
(5)

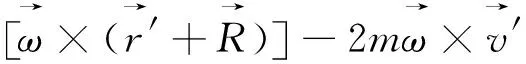
(6)

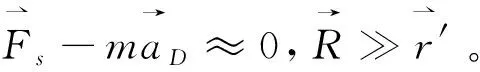
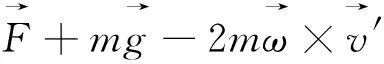
(7)

其中表觀重力由自轉角速度和星球半徑決定

(8)

表觀重力的矢量合成如圖 2所示

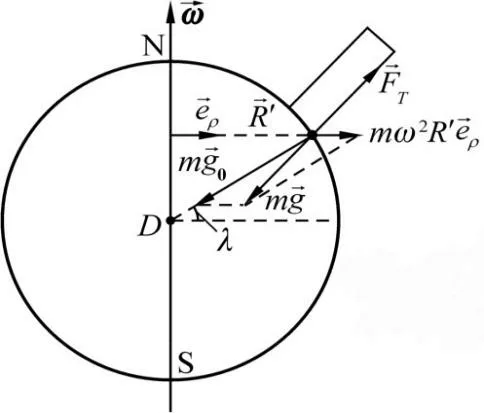
圖2 表觀重力示意圖

1.2 傅科擺的運動微分方程

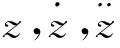
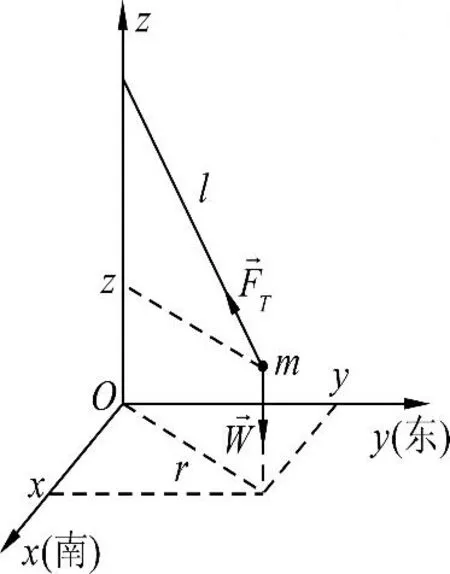
圖3 傅科擺受力示意圖

對于傅科擺，根據非慣性系中的牛頓第二定律有

(9)

其中，

(10)

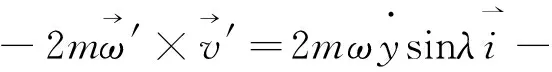
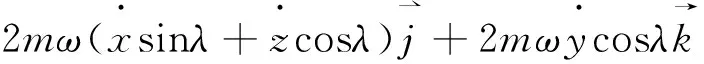
(11)

由此可列出三個方向的運動微分方程

(12)

其中存在約束條件x2+y2+(l-z)2=l2，則可做出以下近似

(13)

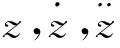
(14)

為了在程序中應用 ode45 指令求解微分方程，將以上微分方程組改寫為一階微分方程組

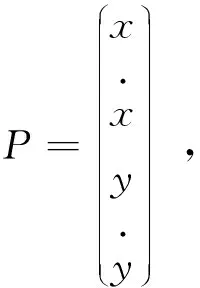
(15)

2 利用App Designer編程仿真模擬

2.1 基于功能的面板設計

為了實現傅科擺的模擬，需要輸入參量并輸出圖像和數據。基于此，設計了如圖 4 所示的面板。

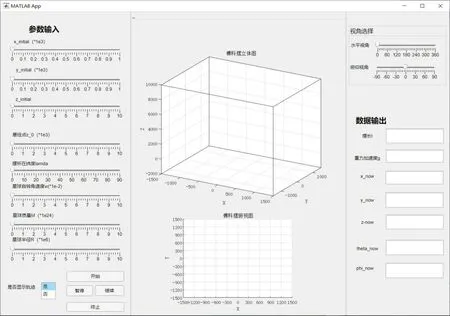
圖4 程序面板

面板分為輸入、畫圖和輸出三個模塊。左側一欄為數據輸入欄，根據第一部分的理論推導，求解傅科擺的微分方程需要以下參量：擺球的初始坐標(x_initial,y_initial,z_initial)、擺球初始速度(默認為 0，由于傅科擺的……