規則波下剛性植物根莖對邊界層最大剪切力特性影響研究

李勰，陳杰,2,3,4*，蔣昌波,2,3,4，姚震，羅元拼，羅婉嬌

( 1. 長沙理工大學 水利與環境工程學院，湖南 長沙 410114；2. 洞庭湖水環境治理與生態修復湖南省重點實驗室，湖南 長沙 410114；3. 水沙科學與水災害防治湖南省重點實驗室，湖南 長沙 410114；4. 湖南省環境保護河湖疏浚污染控制工程技術中心，湖南 長沙 410114)

1 引言

近岸植物與波浪的相互作用一直是海岸研究領域的熱點[1-4]。以紅樹林為代表的剛性植物近岸消波減浪效果顯著[5]，其作為一種新型生態屏障，可起到保護海岸的作用。

許多學者開展了以概化模型模擬近岸植物的研究工作，包括數值模擬[6-7]和實驗研究。在實驗方面，起初學者們多以立體圓柱來模擬剛性植物，如Dalrymple等[8]忽略植物的部分結構特性，以垂直圓柱模擬植物，對規則波下的沿程能量損失做了研究。在此基礎上，部分學者考慮到植物結構上的差異性，以不同的模型模擬植物的根、莖、葉。如Husrin等[9]以真實植物根和莖的剛性模型探究了孤立波下紅樹林的消波特性。但這些學者只考慮了單獨的根、莖、葉對波浪的影響，而忽略了根莖葉之間的配合，三者組合共同對波浪的影響。所以，一些學者優化了實驗及實驗模型，進一步考慮了植物根、莖、葉組合對波浪的影響[10]以及單株和簇狀植物不同的消波特性[11]。但前人的研究大多是分析了波浪的波高[5]、流速[12]、波能衰減[8]等特性，而對波浪經過植物帶的過程中沿程剪切力變化的分析很少。

底部剪切力是引起泥沙輸運而導致泥沙淤積的主要動力，波浪作用下的泥沙運動已有許多學者[13-15]研究，對于波浪剪切力[16-20]研究工作也已經開展。在波浪傳播至紅樹林時，大量剛性植物的存在會引起波浪剪切力的變化，國內外已開展了一些研究工作[21-22]。紅樹林根系發達，專門針對剛性植物根莖結構對波浪剪切力的影響，還有待進一步研究。因此，為彌補現有研究不足，設計了根莖定量概化植物模型，分析剛性植物的根、莖對于規則波下邊界層最大剪切力特性的影響。

2 實驗設置

實驗在長沙理工大學長40.0 m、高0.8 m、寬0.5 m波浪水槽中進行。圖1給出實驗布置情況，水槽右側設置了消能坡，消除波浪反射的干擾，左側設有推板式造波機。水槽中分別設置了編號為G1至G8的浪高儀。2.0 m長的植物模型帶設置在水槽中部。

圖1 實驗布置（單位：m）Fig. 1 Sketch of experment (unit：m)

如圖2a和圖2b所示，實驗設計了變態比尺紅樹林模型，橫向比尺為8∶39，豎向比尺為1∶10。莖高45.0 cm，采用直徑2.0 cm的空心有機玻璃圓柱進行模擬。根高14.1 cm，采用直徑0.8 cm的空心有機玻璃圓柱進行模擬，有機玻璃圓管動態彈性模量E動=4.35×109N/m2、靜態彈性模量E靜=3.15×109N/m2。由于樹根根須數量、根須直徑、對底面投影面積等幾何因素非常復雜，對植物樹根部分僅做概化模型，且該模型材料，在波浪作用下不會產生變形，可以較好地模擬植物樹干部分。如圖2d所示在底部采用有機玻璃底板來固定植物模型，底板尺寸長×寬×高為200.0 cm ×49.5 cm×0.8 cm。單個植物模型根群直徑為10.0 cm，模型橫向邊距為2.6 cm，間距為3.2 cm；縱向邊距為1.975 cm，間距為1.85 cm。

如表1所示，實驗采用規則波為入射波，考慮了兩種水深h、4種波高H和4種周期T。模型分別采用根莖組合（如圖2b所示）、單獨根（圖2b中去掉長莖即為單獨根模型）兩種植物模型型式。

表1 實驗工況Table 1 Expermental cases

圖2 植物模型Fig. 2 Plant models

3 理論分析

對于黏性很小的流體或大雷諾數的流體運動，黏性影響主要限于邊界層，在邊界層內存在著很大的速度梯度和相應的剪切力。針對此次試驗，結合邊界層理論和前人的試驗經驗，可將整個植物帶根群視為邊界層[12]。故在無植物帶水流中，邊界層最大剪切力的位置在底床附近；而含植物帶水流中，邊界層最大剪切力出現在植物帶根群頂部附近。

Jonsson[22]在總結前人研究工作基礎上，對波浪底部邊界層作了較全面的探討，提出波浪作用下邊界層最大剪切力τm可由下式計算：式中，ρ為流體密度，取1 000 kg/m3；fw為波浪底摩阻系數；um為近底波浪質點水平速度的最大值。層流邊界層下的波浪摩阻系數計算式如下：

式中，雷諾數Re計算如下：

式中，μ為水的黏滯系數，實驗室溫度為20℃，取1.01×10-6kPa·s。

底部水質點最大運動振幅am可由下式計算：

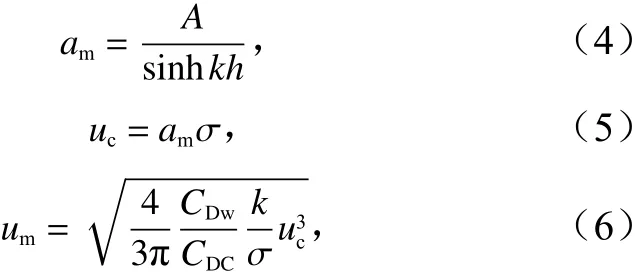
式中，A為振幅，取A=H/2；H為波高；h為水深；k為波數；σ為圓頻率；CDW是瞬時阻力系數；CDC是時均阻力系數，比值取為1.0[21]。

式（5）是基于微幅波理論計算的近底質點水平速度，式（6）則是由Luhar等[12]基于含植物帶的規則波，經過推導，得出的在植物帶中邊界層流速的計算公式。

Jonsson[22]給出波浪的邊界層從層流狀態進入紊流狀態的判斷依據為Re≥1.26×104。

圖3 給出了G3至G7位置的雷諾數計算結果，圖中顯示所有工況下邊界層雷諾數均滿足Jonsson[22]給出的判別式，故邊界層處于層流狀態。

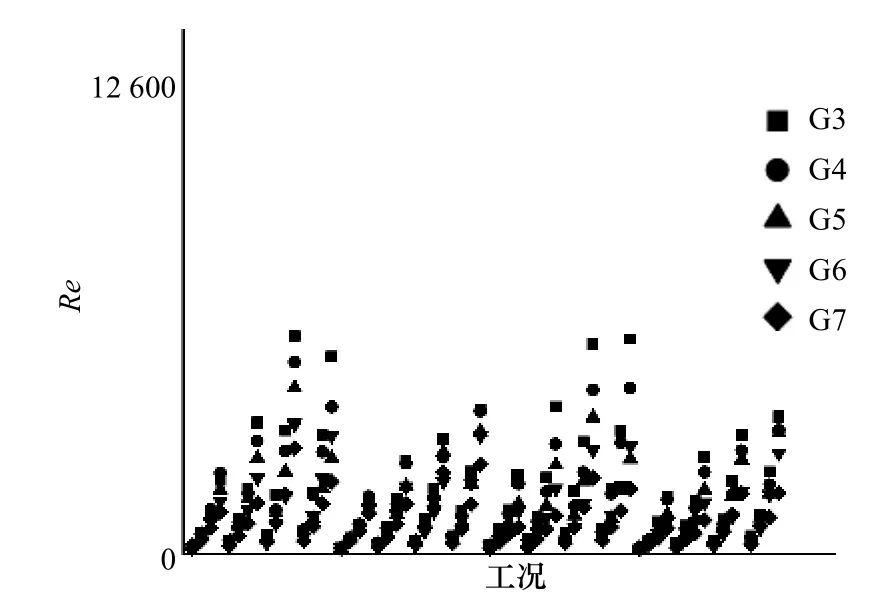
圖3 雷諾數計算結果Fig. 3 Reynolds number calculation results

邊界層最大剪切力可由Jonsson[22]和Luhar等[12]公式計算得到，其中影響邊界層最大剪切力的變量是波高H。植物能夠引起波浪的波高衰減，已經在很多研究中證明。因而以波高為主要影響因素，來探討剛性植物對規則波下邊界層最大剪切力特性的影響。

4 結果分析

4.1 剪切力沿程變化分析

如圖1所示，以G1浪高儀處為原點，沿流向方向為x軸正方向，沿水流正向設計了15株植物模型，沿水流垂向設計了4株植物，共計植物60株，分析圖中植物模型僅為植物帶位置示意，植物個數以圖1為準。G1與G2浪高儀用于驗證入射波波形，G8浪高儀用于分析數據時分離反射波，G3浪高儀放置在植物帶前0.2 m處，用來測量進入植物帶前波浪的波高數據。沿程共設置了5個斷面，分別為G3、G4、G5、G6和G7。為更直觀地體現植物模型對規則波剪切力的影響，對邊界層最大剪切力相對衰減比例τi/τ0在沿程5個斷面的變化進行分析。其中，τ0為基于入射波高所計算的剪切力，τi為特定斷面的剪切力。

圖4 a至圖4h給出單獨根模型下剪切力的沿程變化情況。從總體上看，邊界層最大剪切力τm的衰減效果隨入射波高H的增大而增大。在波浪開始進入植物帶時，波速較大，在剛接觸會產生較大的紊動效應，導致剪切力會有一定幅度的上漲。當h=30 cm時，在x=4.3 m和x=4.9 m位置，邊界層最大剪切力會有一定幅度的增大，且當T=1.9 s時，在x=6.1 m位置，也出現了邊界層最大剪切力變大的情況。而當h=35 cm時，變大位置基本上后移到了x=5.5 m或x=6.1 m處，而在部分工況下，出現了明顯的邊界層效應；在x=6.7 m位置，會出現邊界層最大剪切力衰減強度的回升。在單獨根模型下，波浪在穿過植物帶后，x=6.7 m位置的τi/τ0范圍是0.46～0.85，平均為0.67。

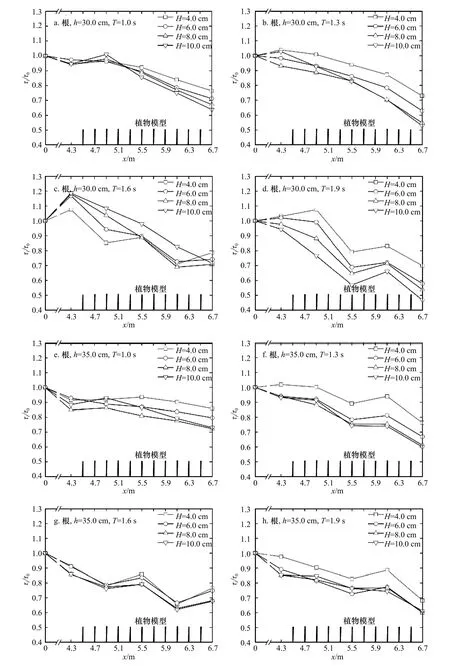
圖4 單獨根模型剪切力沿程衰減規律Fig. 4 The variation of shear force attenuation along the way with roots alone

圖5a至圖5h給出根莖模型下邊界層最大剪切力的沿程變化情況。圖5a至圖5c中，邊界層最大剪切力τm初始有些許增加，隨后急劇下降。圖5d至圖5f中邊界層最大剪切力τm上漲后移到了x=6.1 m位置，在最后一段，會有一個快速的下降。圖5g和圖5h除了在植物帶中出現了上漲情況外，在最后位置也出現了上漲。對比單獨根模型實驗結果，總體上，剪切力的衰減效果隨入射波高的增大而增大，上漲的規律也與根模型類似。根莖模型對剪切力的消減效果是強于根模型的，x=6.7 m位置的τi/τ0范圍由0.46～0.85減小至0.46～0.76，綜合所有工況計算得到x=6.7 m位置的τi/τ0的平均值，可發現平均值由根模型的0.67下降至根莖模型的0.58。由此可見，莖有助于根群減小底部剪切力。

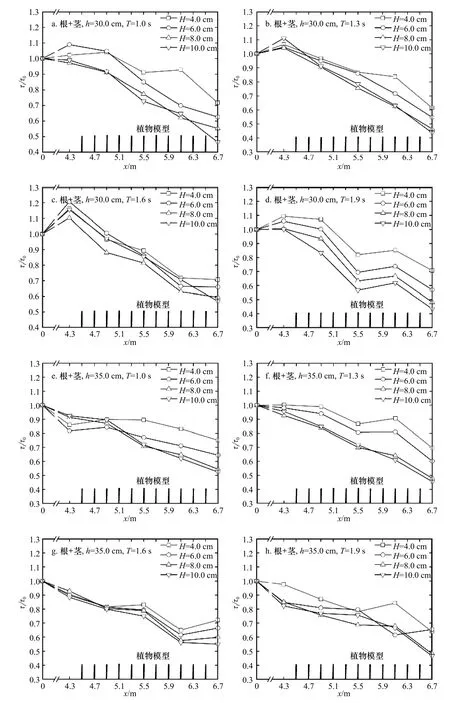
圖5 根+莖模型影響下的剪切力沿程衰減規律Fig. 5 The variation of shear force attenuation along the way with roots and stems

4.2 剪切力衰減系數變化分析

為了更好地分析邊界層最大剪切力在不同模型及不同工況下的變化規律，定義一個剪切力衰減系數K，計算式如下：

式中，τ6和τ3分別是G6和G3斷面的剪切力值。

圖6 給出式（7）計算得到邊界層最大剪切力消減系數隨波高的變化規律。其中圖6a和圖6b是根模型的邊界層最大剪切力消減系數隨波高的變化圖。從圖中可以看出，雖然有部分區域由于水流的紊流效應，消減系數會有降低的趨勢，但整體上看消減系數還是隨入射波高的增大而增大。T=1.3 s和1.9 s時的消減系數時大于T=1.0 s和1.6 s。圖6c和圖6d是根莖模型的邊界層最大剪切力消減系數隨波高的變化圖。消減系數也是隨入射波高的增大而增大，且根莖模型的消減系數整體略大于單獨根模型的消減系數。同樣于根模型T=1.3 s和1.9 s時的消減系數時大于T=1.0 s和1.6 s。根莖組合模型消減系數范圍為0.12～0.61，單獨根模型消減系數范圍為0.06～0.51。

4.3 剪切力消減系數與水動力因素、植物因素之間的關系

波浪傳播過程中的邊界層最大剪切力變化與諸多因素有關。目前學者主要將其分為兩類：水動力因素和植物因素[23]。本實驗中，影響規則波與植物相互作用的水動力因素包括入射波高H、周期T、水深h、波長L等，影響其規律的植物因素包括：植物高度hv、植被區沿流線長度B、淹沒體積Vv。因而剪切力消減系數與要素之間存在以下關系：

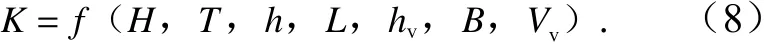
將式（9）中的參數無量綱化得到式（10）

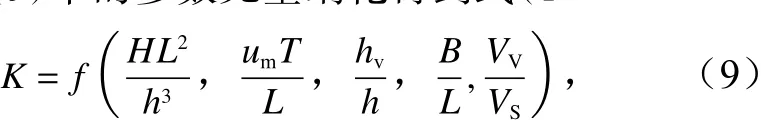
式中，HL2/h3為厄塞爾數，表示流體層中長的表面重力波的非線性程度；umT/L為KC數，表示黏性力相對慣性力之間的關系；hv/h為淹沒度，從垂向方面考慮植物高度與水深的影響；B/L為植被區相對寬度，是從縱向方面考慮植物帶長度和波長的影響；Vv/Vs為植被區相對淹沒體積，來表示植物相對體積的影響。

為進一步分析式（9）中邊界層最大剪切力消減系數K與各影響因子之間的關系，基于單獨根和根莖植物模型的實驗數據，對式（9）進行多元非線性回歸擬合。得到了剪切力消減系數K與厄塞爾數HL2/h3，KC數umT/L、淹沒度hv/h、植被區相對寬度B/L、植被區相對淹沒體積Vv/Vs之間的關系，結果如式（10）所示。由于受到多個水動力因素和植物因素的影響，植物對邊界層最大剪切力的消減機理十分復雜，擬合情況如圖7所示，雖然整體數據點和擬合曲線存在部分偏差，但整體呈現冪函數的關系。擬合公式與實驗數據之間擬合度達到0.772。其中，實測值與理論值相

差30%的工況有：單獨根模型8個（h=35 cm，H=4 cm，T=1 s；h=35 cm，H=8 cm，T=1 s；h=35 cm，H=10 cm，T=1 s；h=35 cm，H=4 cm，T=1.3 s；h=35 cm，H=6 cm，T=1.6 s；h=35 cm，H=8 cm，T=1.6 s；h=35 cm，H=10 cm，T=1.6 s；h=35 cm，H=4 cm，T=1.9 s）。根+莖模型4個（h=35 cm，H=4 cm，T=1 s；h=35 cm，H=4 cm，T=1.6 s；h=35 cm，H=6 cm，T=1.6 s；h=35 cm，H=6 cm，T=1.9 s）。綜合來看，誤差較大的點均為水深h為35 cm的工況，故此擬合公式更適用于水深較淺的情況。且單獨根模型的誤差點多于根+莖模型，也從側面體現了莖有助于根群減小波浪底部剪切力。式（10）體現了消減系數變化與水動力因素和植物因素均存在著物理聯系，其中，消減系數K與厄塞爾數HL2/h3、植被區相對寬度B/L呈負相關，與KC數umT/L、淹沒度hv/h，植被區相對淹沒體積Vv/Vs呈正相關。

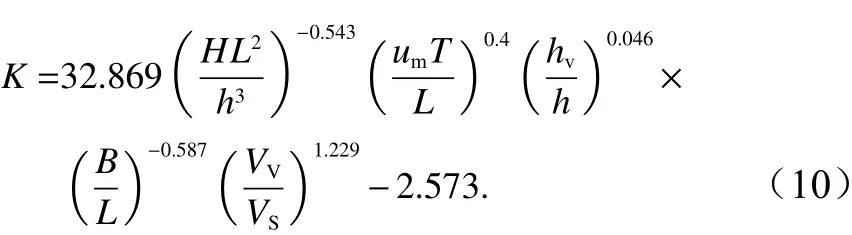
5 結論

本實驗研究探究的主要內容是規則波經過含植物帶水流時，位于邊界層的最大剪切力是如何變化的。著重討論植物模型對于邊界層最大剪切力的影響特性，為以后學者研究紅樹林帶邊界層最大剪切力提供理論依據。通過概化植物模型實驗，探究了單獨根、根莖共同作用下近岸剛性植物對規則波沿程剪切力衰減特性及衰減系數變化規律，研究發現邊界層最大剪切力的衰減系數的范圍為0.06～0.61，說明紅樹林是能夠影響到波浪邊界層最大剪切力，且能使其減小。規則波下邊界層最大剪切力衰減效果隨波高的增大而增大，且紅樹林的莖有助于根群減小底部剪切力。植物根莖模型對邊界層最大剪切力變化特性的影響與淹沒度、植被區相對淹沒體積、植被區相對寬度、厄塞爾數及KC數均有關系。本實驗僅考慮含植物帶水流邊界層最大剪切力的理論研究，研究有助于進一步探究以紅樹林為代表的近岸剛性植物對波浪邊界層剪切力的特性影響，為合理利用近岸剛性植物減少海岸帶泥沙淤積、抵御海浪侵蝕提供一定指導。