基于干凈數據的流形正則化非負矩陣分解

李 華，盧桂馥，余沁茹

（安徽工程大學計算機與信息學院，安徽蕪湖 241000）

（?通信作者電子郵箱luguifu_jsj@163.com）

0 引言

隨著信息社會進入大數據時代，高維數據的增長給數據處理帶來了極大的挑戰，有效的數據表示不但能夠提升算法的性能，而且有助于人們發現高維數據背后隱藏的低維本征結構。如何找到原始高維數據的有效低維表示是近年來的一個研究熱點［1-4］。很多研究者做了大量的工作來挖掘蘊含在原始數據的內在結構，其中矩陣分解是一種常用的技術。通過矩陣分解算法可以獲取高維數據的低秩表示，從而有效地挖掘出蘊含在原始圖像數據中的有用信息，使新的數據表示具有更好的識別能力［5-8］。常見的矩陣分解算法有：正交三角分解（QR分解）［9］、非負矩陣分解（Nonnegative Matrix Factorization，NMF）［10-12］等。其中，NMF 是由Lee 等［11］于1999年在《Nature》雜志上提出的，其心理學和生理學的構造依據是對整體的感知是由組成整體的部分感知所構成的，這也恰恰符合人類大腦對事物的直觀理解。它基于數據的局部特征提取數據信息，分解之后的矩陣中所有元素都是非負的，是一種有效的圖像表示工具。

NMF 自提出之后便得到學者的廣泛關注并對其進行了深入的研究。為了提高算法的識別率和有效性，研究人員在NMF 的基礎上提出了許多原始NMF 算法的變體，試圖從不同的角度對NMF進行改進。Hoyer［13］把稀疏編碼和標準NMF算法結合，提出非負稀疏編碼（Non-negative Sparse Coding，NSC）算法，使得矩陣分解后系數矩陣的稀疏性較好，這樣可以用更少的有用信息來表達原有信息，在一定程度上提高了運算的效率。Zhou 等［14］在圖正則化非負矩陣分解（Graph regularized Nonnegative Matrix Factorization，GNMF）算法的基礎上為NMF 添加了額外的約束，進一步提出了局部學習正則化NMF（Local Learning regularized NMF，LLNMF）。Wang等［15］提出了一種降維局部約束圖優化（Locality Constrained Graph Optimization for Dimensionality Reduction，LC-GODR）算法，將圖優化和投影矩陣學習結合到了一個框架中，由于圖是預先構造并保持不變的，使得其在降維過程中的圖形可以自適應更新。為了能夠同時利用數據的全局信息和局部信息來進行圖形的學習，Wen 等［16］提出了一種自適應圖正則化的低秩表示（Low-Rank Representation with Adaptive Graph Regularization，LRR-AGR）方法。為了同時考慮數據空間和特征空間的流形結構，Meng等［17］提出了一種具有稀疏和正交約束的對偶圖正則化非負矩陣分解（Dual-graph regularized Non-negative Matrix Factorization with Sparse and Orthogonal constraints，SODNMF）。萬源等［18］提出了一種低秩稀疏圖嵌入的半監督特征選擇方法（semi-supervised feature selection for Low-Rank Sparse graph Embedding，LRSE），充分利用有標簽數據和無標簽數據，分別學習其低秩稀疏表示，在目標函數中同時考慮數據降維前后的信息差異和降維過程中的結構信息，通過最小化信息損失函數使數據中的有用信息盡可能地保留下來，從而可以選擇出更具判別性的特征。Tian 等［19］提出了一種總方差約束圖正則化凸非負矩陣分解（Total Variation constrained Graph-regularized Convex Non-negative Matrix Factorization，TV-GCNMF）算法，將總方差和拉普拉斯圖及凸NMF 結合起來，既保留了數據的細節特征，又揭示了數據特征的內在幾何結構信息。

為了揭示數據內在的流形數據，考慮到數據所攜帶的幾何信息，Cai 等［20］在標準NMF 的基礎上提出了圖正則化非負矩陣分解（GNMF）算法，并在實驗數據集上獲得了較好的實驗結果。為了獲得原始圖像數據集的低秩結構，Li 等［21］提出了圖正則化非負低秩矩陣分解（Graph Regularized Nonnegative Low-Rank Matrix Factorization，GNLMF）算法，該算法雖然考慮了利用低秩信息來增強算法的魯棒性，但其本質上是一種兩階段方法，且由于不能循環迭代，使得其得到的解不是最優的。為了獲得數據的局部和全局表示，Lu 等［22］提出了低秩非負分解（Low-Rank Nonnegative Factorization，LRNF）算法。雖然LRNF 的性能較為優異，但它并沒有考慮數據的流形結構信息，并且在求解過程中沒有明確說明是如何來保證數據非負性的。

研究表明，一方面，原始圖像的有效信息常隱藏在數據的低秩結構中，數據通常從嵌入在高維中的低維流形上進行采樣；另一方面，在NMF 中添加額外的正則化項可以在一定程度上提高算法抗噪聲干擾的能力和算法的魯棒性。為了解決上述問題，本文提出一種基于干凈數據的流形正則化非負矩陣分解（Manifold Regularized Non-negative Matrix Factorization with low-rank constraint based on Clean Data，MRNMF/CD）算法，該算法將含有噪聲的原始圖像數據進行清洗，使用干凈數據進行學習，并且將有效低秩結構和數據的幾何信息引入到NMF，使其魯棒性有了進一步提高。通過在ORL、COIL20 和Yale 三個公開數據集上進行實驗，驗證了本文MRNMF/CD 算法比現有的其他算法優異。

1 相關工作

1.1 魯棒性主成分分析（RPCA）

作為最重要的降維方法之一，主成分分析（Principal Component Analysis，PCA）已應用于很多領域。但由于數據中的噪聲和異常值，PCA 的性能及應用受到了限制。為了克服PCA 的這些不足，人們提出了魯棒性PCA（Robust PCA，RPCA）［23-24］用于恢復帶有誤差的數據原子空間結構［25-26］。

RPCA 假定原始數據為X=(A+E)T∈Rn×m，A∈Rm×n為低秩數據矩陣，E∈Rm×n為添加的噪聲誤差矩陣。RPCA 的目標是恢復數據的噪聲部分，其優化模型為：

其中：α為正參數；‖ · ‖0為矩陣的l0范數。由于模型（1）為非凸的，所以很難得到有效的解。通過將秩函數與l0范數轉換為核范數與l1范數，則式（1）轉化為下式：

其中：α為正參數，‖ · ‖*表示矩陣的核范數，‖ · ‖1表示矩陣的l1范數。

1.2 圖正則化非負矩陣分解（GNMF）

現實世界中，許多數據是嵌入在高維歐氏空間中非線性低維流形上的，然而，NMF 算法和許多改進的NMF 算法在處理原始數據時，沒有考慮數據的內蘊幾何結構。為了能夠發現數據隱藏信息的表示方法，同時又考慮數據內在的幾何信息，Cai 等［20］通過將圖正則化項融入標準的NMF 框架中，提出了圖正則非負矩陣分解算法。該算法假設2 個數據點在原始數據空間中的幾何距離如果是鄰近，則其在基于新的基向量低維表示中相對應的數據點也應該離得很近。與傳統的降維算法相比，流形學習算法能夠揭示原始數據內在的幾何結構，尋找高維數據在低維空間中的緊致嵌入。GNMF 的目標函數為：

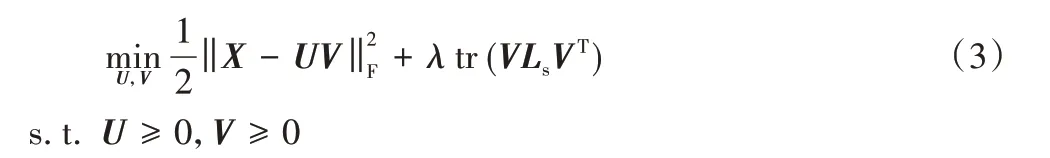
其中：tr(VLsVT)是圖正則化項，Ls是圖拉普拉斯矩陣，圖正則化參數λ＞0。

Cai等在文獻［20］中給出了如下的迭代規則：

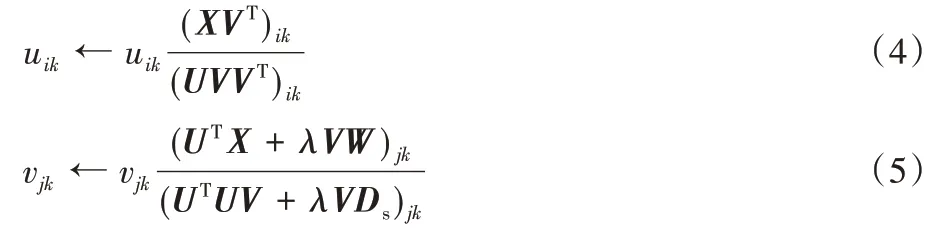
其中：Ds是對角矩陣，W是數據點間的相似度矩陣，Ls=Ds-W。

2 基于干凈數據的流形正則化非負矩陣分解

研究表明，使用去噪聲的干凈數據進行學習有利于恢復數據的原子空間結構，提高算法的魯棒性和抗干擾能力；并且，原始圖像的有效信息常常隱藏在它的低秩結構中，而流形正則化可以保留數據的局部幾何結構信息。本文提出的算法，不僅考慮了數據的魯棒性，使用了去除噪聲的干凈數據進行低秩非負矩陣分解，而且加入了流形正則化項，從而保留了數據的局部幾何結構信息。

2.1 算法模型

給定一個訓練集X=[x1，x2，…，xn]∈Rm×n，設E為噪聲矩陣，令X=A+E，稱A為不含噪聲的干凈數據。使用訓練的干凈數據矩陣A進行NMF 分解，將其分為兩個非負因子矩陣的乘積，得到：

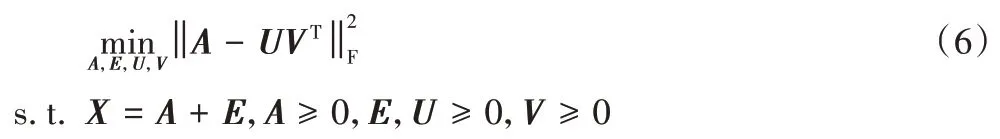
上式僅學習了局部信息而忽略了數據的低秩信息，于是引入低秩約束，得到：

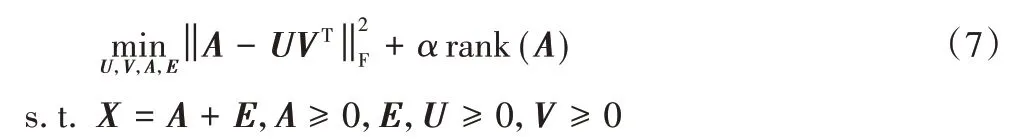
其中：α＞0，是衡量低秩矩陣A的權值。考慮到此式是NP 難問題，結合RPCA理論，進一步使用下式代替求解：

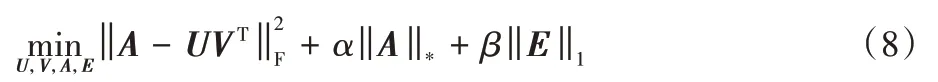
最后，為了利用數據的局部幾何結構信息，加入局部圖拉普拉斯約束，得到本文算法的最終目標函數：

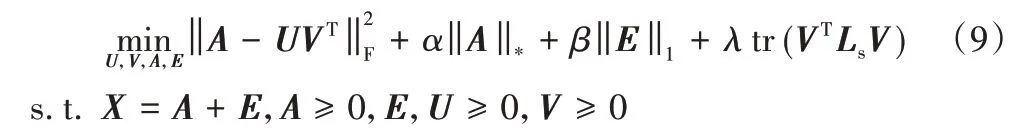
其中權值系數α、β和λ均大于0。目標函數的第一項執行干凈數據矩陣A的低秩非負矩陣分解；第二項和第三項表示原始數據經清洗，去掉噪聲E，確保用于非負矩陣分解的數據矩陣A是干凈的；第四項是圖正則化項，保留了圖的幾何信息。

2.2 模型求解

本節考慮如何對目標函數式（9）進行求解。通過引入輔助變量B，則目標函數式（9）變為：

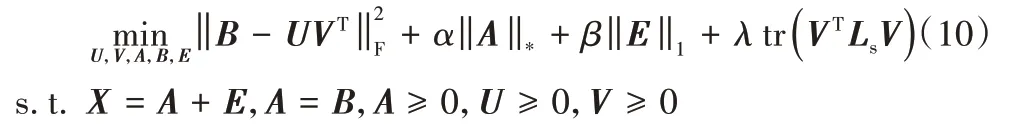
接下來使用增廣拉格朗日法對式（10）進行求解，其增廣拉格朗日函數為：

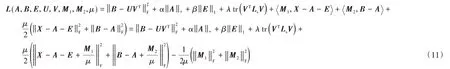
2.2.1 變量A的求解

固定其他變量來計算A，求解式（10）等價于求解：

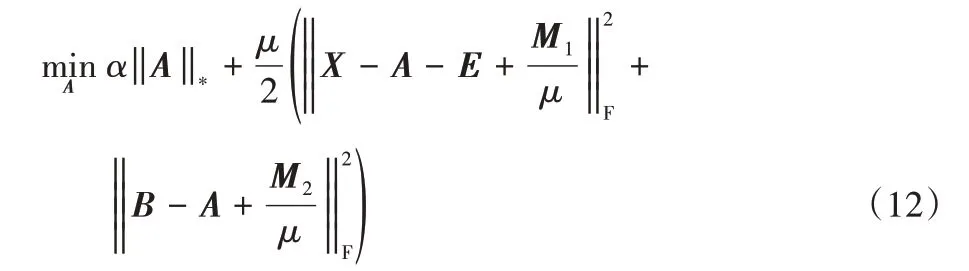
進一步推導，可得：

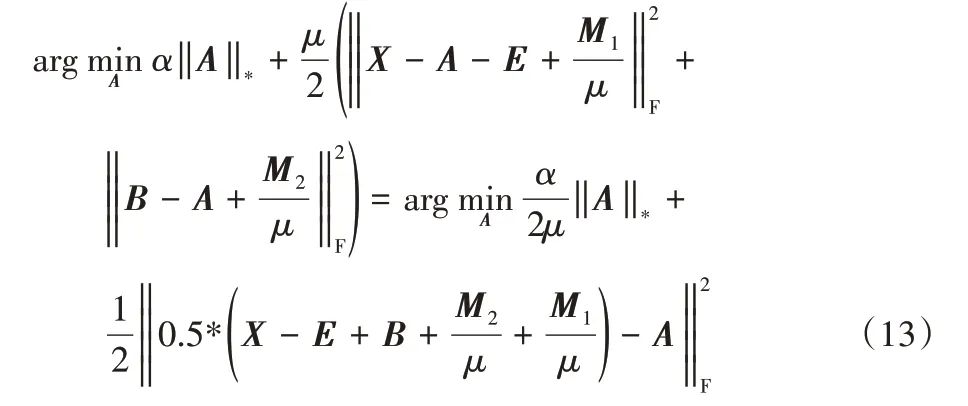
該式可用奇異值閾值法（Singular Value Thresholding，SVT）［27］求解，設的SVD［28］為：

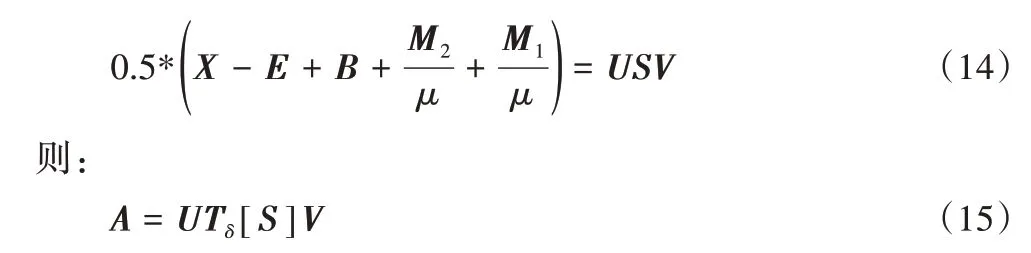
2.2.2 變量E的求解

固定其他變量來計算E，求解式（10）等價于求解下式：

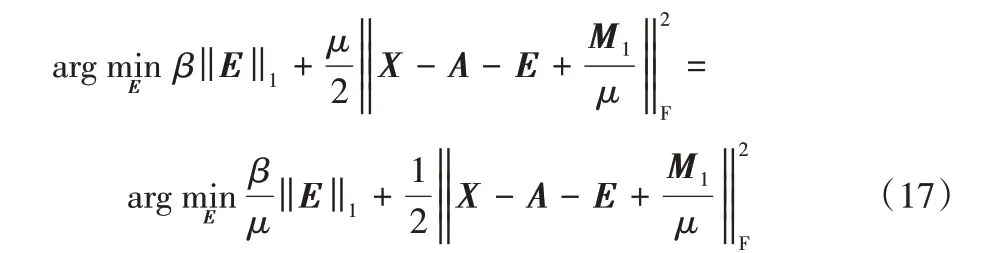
該問題可用shrinkage operator［24］求解。

2.2.3 變量B的求解

固定其他變量來計算B，求解式（10）等價于求解下式：

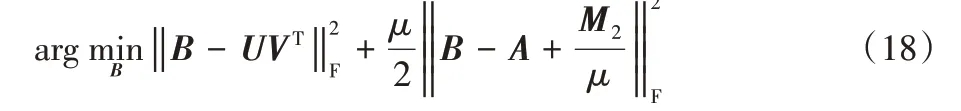
進一步推導得到：

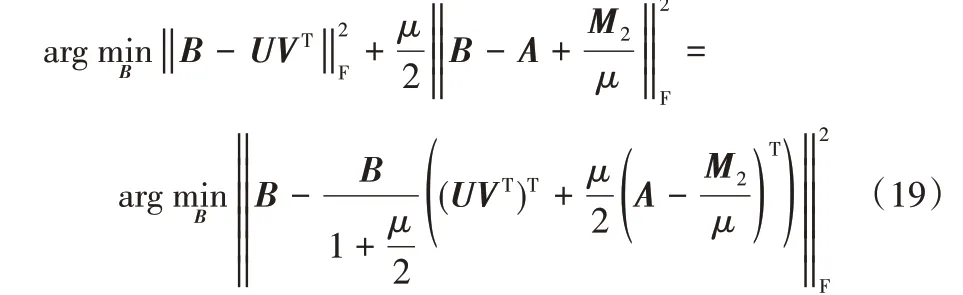
2.2.4 變量U的求解

固定其他變量來計算U，求解式（10）等價于求解下式：

根據矩陣跡的性質，tr(AB)=tr(BA)和tr(A)=tr(AT)，得到：

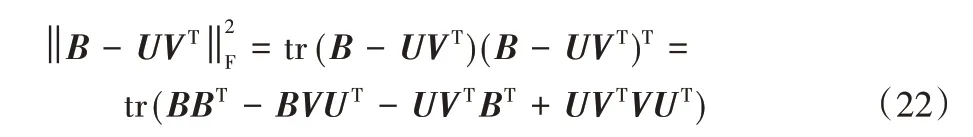
令φik為約束uik≥0 的拉格朗日乘子，定義Φ=[φik]，則拉格朗日函數L(U)為：

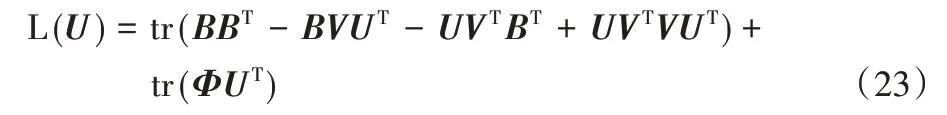
通過式（23）對U求偏導，得到：

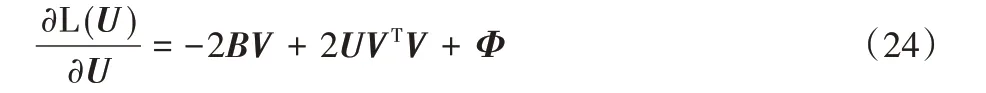
根據Karush-Kuhn-Tuchker（KKT）條件［29］，φikuik=0，得到以下方程：

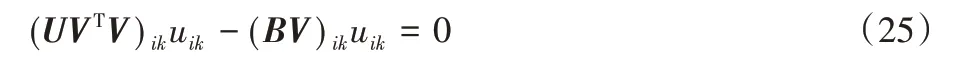
因此得到uij的更新規則：

2.2.5 變量V的求解

固定其他變量來計算V，求解目標函數式（10）等價于求解下式：

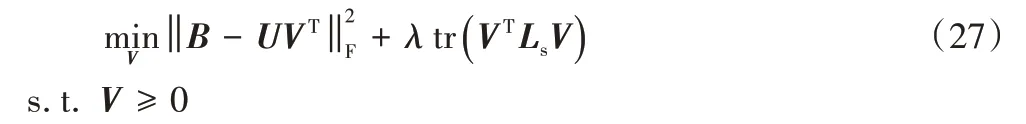
根據矩陣跡的性質，tr(AB)=tr(BA)和tr(A)=tr(AT)，得到：

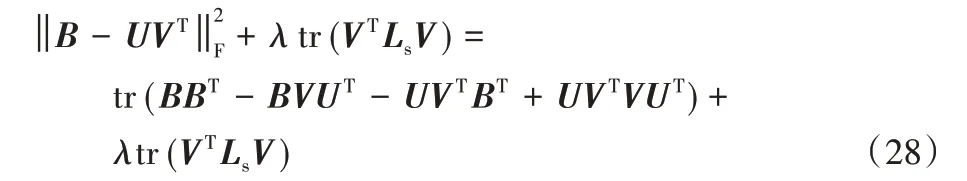
令φjk為約束vjk≥0的拉格朗日乘子，定義Ψ=[φjk]，則拉格朗日函數L(V)為：

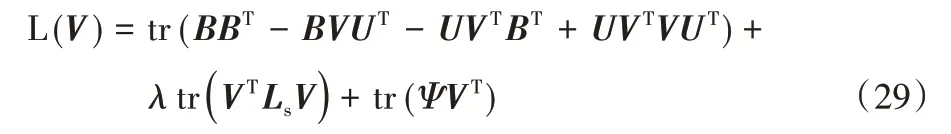
通過式（29）對V求偏導，得到：

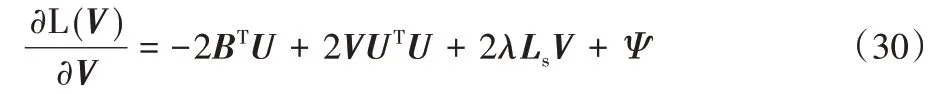
根據KKT條件［29］，φjkvjk=0，得到以下方程：

因此得到vjk的更新規則

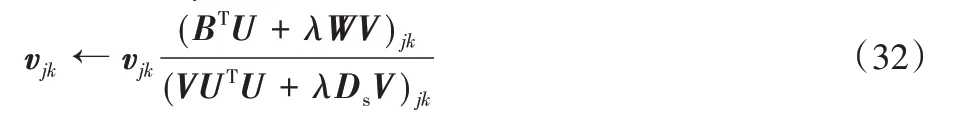
2.2.6 更新變量μ，M1，M2

最后，按照式（33）更新變量μ、M1、M2：

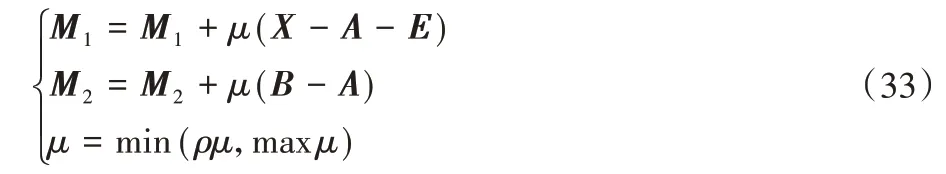
2.3 收斂性分析

本節討論MRNMF/CD算法的收斂性。

定理1 對于U≥0，V≥0，式（10）中的目標函數值在式（15）、（17）、（20）、（26）、（32）中的更新規則下不增加，因此MRNMF/CD算法收斂。

證明 顯然，式（15）、（17）、（20）可分別用第2.2.1 節、2.2.2節和2.2.3節中描述的閉式解來解決。因此，只需要證明式（26）和式（32）在每次迭代中的更新規則下目標值是不增加的。此外，因為式（10）中目標的第二項與U無關，第一項在計算V時不涉及U值的更新，且計算得出V后的操作符合標準NMF，所以MRNMF/CD中的U更新規則與原始NMF完全相同，因此，可以使用NMF 的收斂性證明來證明在等式中更新規則下目標沒有增加。有關詳細信息，可參考文獻［30］。

現在，只需要證明在式（32）中的更新規則下，目標函數不會增加即可。而式（32）中更新規則其實等價于文獻［31］中式（26），式（32）的收斂證明可參考文獻［31］附錄中證明過程，此處不列出。

2.4 時間復雜度分析

本節討論本文算法的計算復雜度。在算法MRNMF/CD中，第1 步的復雜度為O(mn2)，第2 步的主要步驟的復雜度為O(mn)，第3 步的計算復雜度為O(mnk)，第4 步的計算復雜度為O(mnk)+O(mnk)=O(mnk)，因此算法MRNMF/CD 的總計算復雜度為O(t(mn2+mnk))，其中t為迭代次數。表1 給出了ORL 數據集上NMF、GNMF、MRNMF/CD 算法的實際運行時間。從表1中可以看出，MRNMF/CD 算法復雜度比較高，這主要是因為在MRNMF/CD 算法中，需進行多次SVD，而SVD 的算法復雜度相對較高。這可能會限制應用程序使用具有大量樣本的數據。降低算法復雜度的常用方法之一是使用PROPACK進行部分SVD，或者使用文獻［32］中的方法，即：

表1 不同算法在ORL數據集上的運行時間對比Tab.1 Running time comparison of different algorithms on ORL dataset

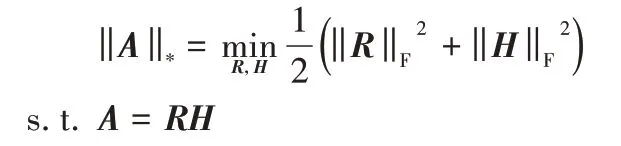
此方法避免了多次SVD，從而降低算法的時間復雜度。在其他數據庫中，MRNMF/CD 算法與其他比較方法在運行時間上的差異與ORL數據集類似。

算法 MRNMF/CD。

輸入 訓練集數據矩陣X∈Rm×n+，參數α、β和λ；

初始化：

B=A，E=0，U=0，V=0，M1=M2=0，μ＞0，λ=0，ρ=0；

迭代：

1）分別使用式（15）、（17）、（20）、（32）、（26）更新A、E、B、V和U；

2）使用下式更新拉格朗日乘子：

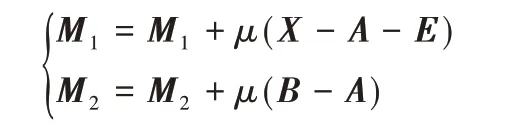
3）更新μ，μ=min(ρμ，maxμ)；

4）t=t+1；

5）得到最優的A、E、B、U、V；

輸出 非負矩陣U和V。

3 實驗及結果分析

為了評估本文提出的基于干凈數據的流形正則化的低秩非負矩陣分解算法MRNMF/CD 的性能，在ORL 人臉數據集、Yale 人臉數據集和COIL20 圖像數據集三個圖像數據集上進行實驗，表2 給出了各數據集及其特征，部分示例圖見圖1。本文實驗條件為11th Gen Intel Core i7-1165G7 @ 2.80 GHz，16 GB DDR3 內存，Matlab2018b。以聚類準確率（ACCuracy，ACC）、標準互信息（Normalized Mutual Information，NMI）兩個指標作為參考，實驗的對比算法為k-means、PCA、NMF 和GNMF，實驗中所用算法的參數已結合原論文根據需要調節至最優。

圖1 ORL、Yale和COIL20數據集中的部分圖像示例Fig.1 Some examples of images in datasets ORL，Yale and COIL20

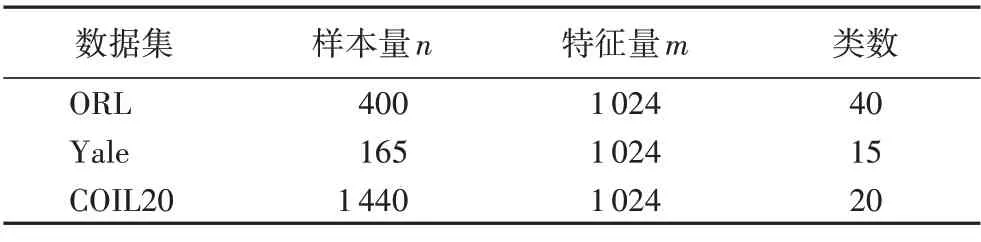
表2 實驗數據集及其特征Tab.2 Experimental datasets and their characteristics

在每個數據集上都進行了算法精度測試，每個數據集均進行5 次聚類實驗，簇數根據各數據集特征量均勻選取，并對5 次測試取平均值來獲得最終的性能得分。對于每個測試，首先應用比較算法中的每個算法，以學習數據的新表示形式，然后在新的表示空間中應用k-means。用不同的初始化將k-means 重復20 次，并記錄關于k-means 的目標函數的最佳結果。

3.1 比較算法

對比算法介紹如下：

1）k-means：在原始數據集上進行，不使用樣本中包含的任何信息；

2）PCA：能夠有效地提取原始數據集中的主要成分；

3）NMF：試圖找出2個非負低維矩陣，其乘積近似為原始矩陣；

4）GNMF：試圖通過構造一個簡單的圖來包含數據中的內在幾何結構信息；

5）MRNMF/CD：使用去噪聲的干凈數據進行非負低秩矩陣分解，并且考慮了數據內在幾何結構信息，實驗中，參數α和β均設為0.1，圖正則化參數設置為10。

3.2 圖像聚類實驗

3.2.1 ORL數據集上的測試

ORL 數據集上的測試結果如表3 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分別為64.61%和77.24%，與GNMF 相比，分別提高了11.91 和19.89 個百分點；與NMF 相比，分別提高了29.01 和39.99 個百分點；與PCA 相比，分別提高了27.61 和38.34 個百分點；與k-means 相比，分別提高了25.11和36.19個百分點。

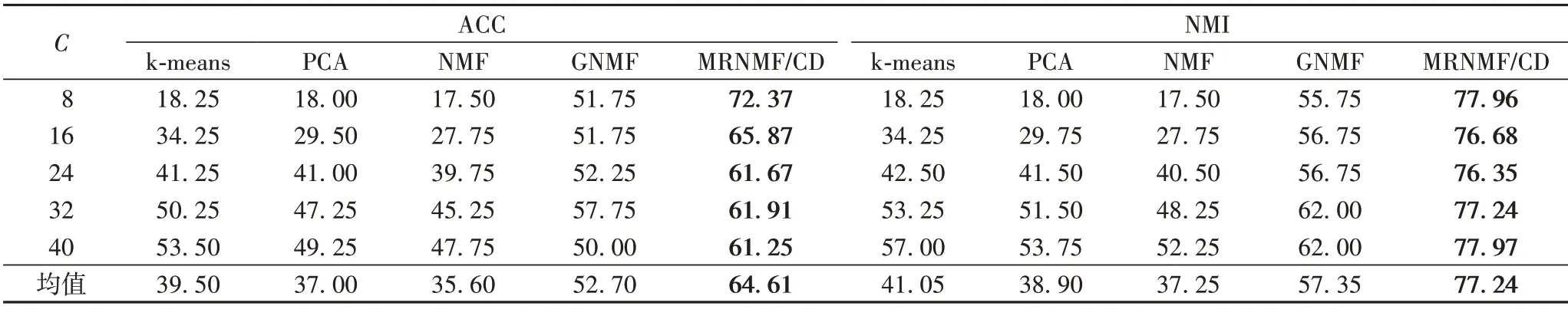
表3 ORL數據集上的聚類結果對比 單位：%Tab.3 Clustering results comparison on ORL dataset unit：%

3.2.2 Yale數據集上的測試

Yale 數據集上的測試結果如表4 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分別為48.90%和42.33%，與GNMF 相比，分別提高了9.14 和1 個百分點；與NMF 相比，分別提高了20.17 和12.63 個百分點；與PCA 相比，分別提高了20.29 和12.87 個百分點；與k-means 相比，分別提高了20.43和13.48個百分點。

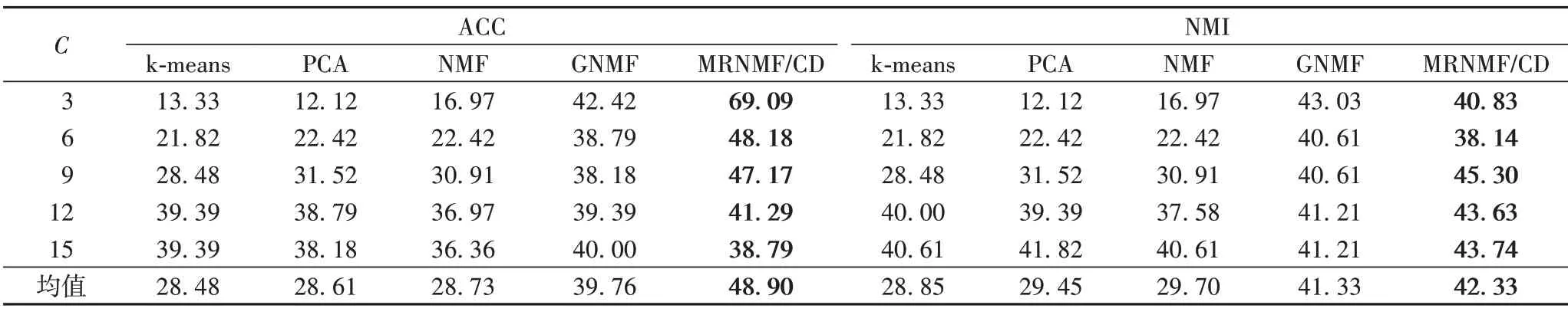
表4 Yale數據集上的聚類結果 單位：%Tab.4 Clustering results on Yale dataset unit：%

3.2.3 COIL20數據集上的測試

COIL20 數據集上的測試結果如表5 所示。可以看出MRNMF/CD 的ACC 和NMI 均值分別為59.91%和64.63%，與GNMF相比，分別降低了2.55和0.58個百分點；與NMF相比，分別提高了16.16 和20.34 個百分點；與PCA 相比，分別提高了19.13 和22.67 個百分點；與k-means 相比，分別提高了17.22和20.85個百分點。

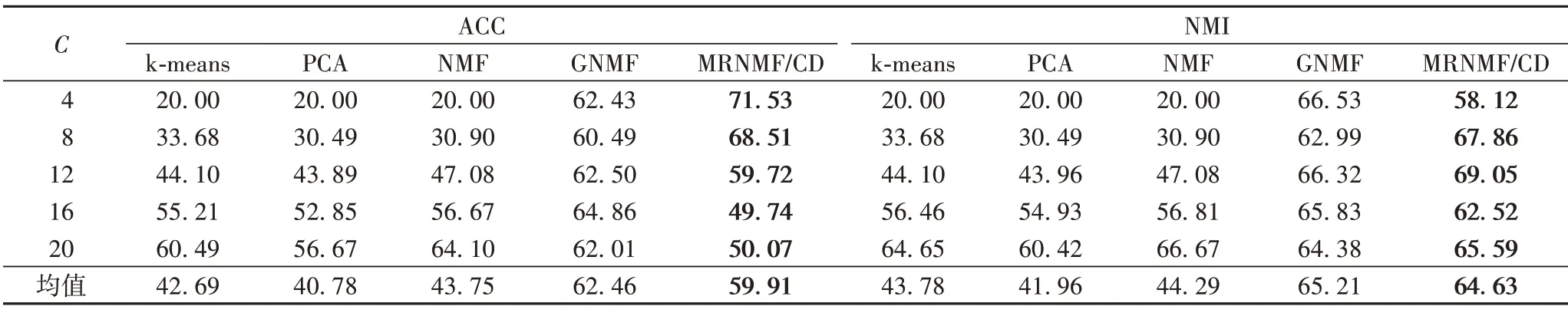
表5 COIL20數據集上的聚類結果 單位：%Tab.5 Clustering results on COIL20 dataset unit：%

3.3 參數選擇實驗

本節對算法中參數α、β和γ的選擇進行討論，分別在ORL、Yale 和COIL20 三個數據集上測試參數α、β和γ對MRNMF/CD 算法性能的影響。所有實驗均使用ACC 指標作為算法評價的標準。為了公平地比較，在每個參數設置下，均會獨立重復實驗20 次。同時，記錄了所有比較方法的最佳平均結果。本節所有方法的迭代次數都根據經驗設置為50，聚類的數量設置為等于真實類的數量。在三個數據集上，分別測試參數α、β和γ值在{0.01，0.1，1，10，100}范圍的聚類精度變化。實驗結果如圖2 所示。可以看出，對于參數α，在ORL數據集上當α=1 時可獲得較好結果，在Yale 數據集上當α=0.1時可獲得較好結果，在COIL20 數據集上當α=1時可獲得較好結果；對于參數β，在ORL 數據集上當β=100 時可獲得較好結果，在Yale 數據集上當β=0.1 時可獲得較好結果，在COIL20 數據集上當β=1 時可獲得較好結果；對于參數γ，在ORL 數據集上當γ=0.01 時可獲得較好結果，在Yale 數據集上當γ=0.01時可獲得較好結果，在COIL20數據集上當γ=1時可獲得較好結果。

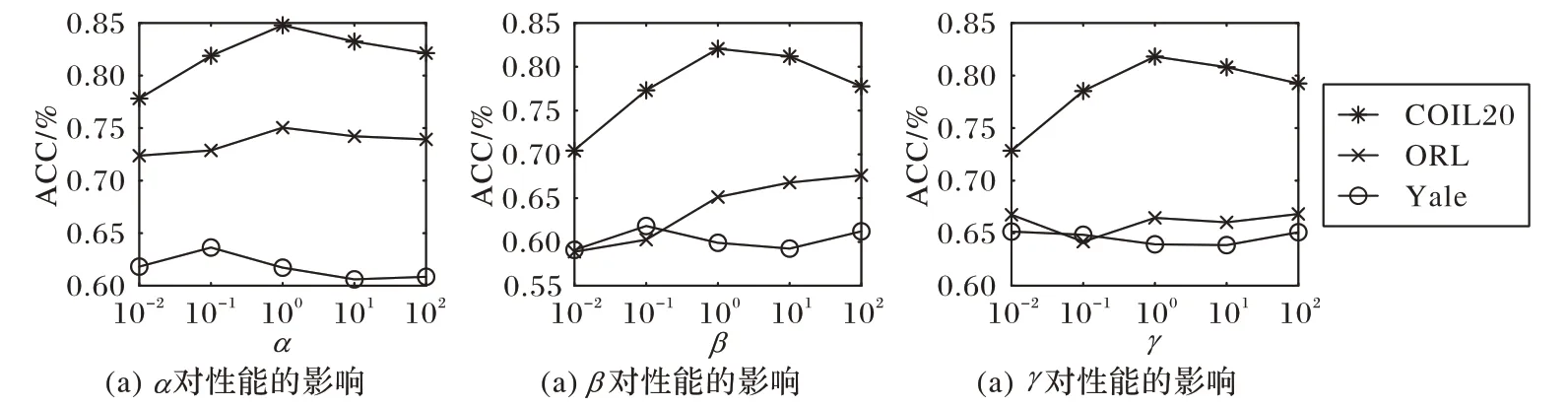
圖2 MRNMF/CD算法中各參數對性能的影響Fig.2 Influence of each parameter on accuracy in MRNMF/CD algorithm

3.4 收斂性研究

本節通過實驗驗證MRNMF/CD 方法的收斂情況。圖3呈現了MRNMF/CD 算法在Yale、COIL20 和ORL 三個數據集上的收斂情況。可以看出，當迭代次數大于35 時，MRNMF/CD算法的目標函數值在Yale 數據集上趨于平穩；當迭代次數大于650 時，MRNMF/CD 算法的目標函數值在COIL20 數據集上趨于平穩；當迭代次數約大于10 時，MRNMF/CD 算法的目標函數值在ORL 數據集上趨于平穩。因此，MRNMF/CD 算法在幾個數據集上均收斂，且速度較快。

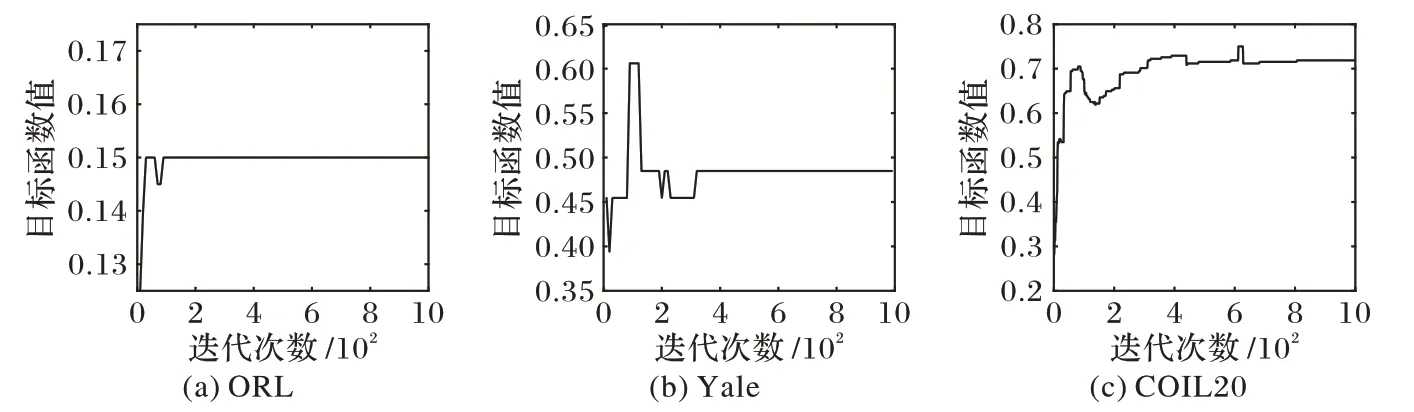
圖3 MRNMF/CD算法在Yale、COIL20和ORL數據集上的收斂曲線Fig.3 Convergence curves of MRNMF/CD algorithm on datasets Yale，COIL20 and ORL

4 結語

本文提出的基于干凈數據的流形正則化非負矩陣分解（MRNMF/CD）算法，考慮原始圖像數據集噪聲干擾和異常值，使用去噪聲的干凈數據進行矩陣分解，具有一定的魯棒性，并且在圖嵌入和數據重構函數中考慮了有效低秩結構和幾何信息，提高了算法的性能。本文還給出了MRNMF/CD 的迭代公式和收斂性證明。最后，MRNMF/CD 在ORL、Yale 和COIL20數據集上的實驗表現出比較好的識別率和優越性。