汽車自動變速器行星輪系數形結合推導速比公式

馮詠軍，關崴，唐諒，袁小星，王墨

汽車自動變速器行星輪系數形結合推導速比公式

馮詠軍，關崴，唐諒，袁小星，王墨

（哈爾濱東安汽車發動機制造有限公司技術中心，黑龍江 哈爾濱 150000）

文章推導了單行星以及雙行星輪系齒輪機構的特性方程式。通過行星齒輪機構變速器的特性方程式，可以分析自動變速器各擋位的速比，為提高計算效率，推導出應用圖形法來計算自動變速器速比的方法。

自動變速器[1]；行星齒輪機構；特性方程式；辛普森式行星輪系；拉維納式行星輪系

引言

目前汽車自動變速器所采用的齒輪機構主要有兩類：單行星輪系結構和雙行星輪系結構[2]。單行星輪系和雙行星輪系都由四部分組成，分別為太陽輪，齒圈，行星輪和行星架，二者的區別在于雙行星輪系有兩個行星輪，單行星輪系只有一個行星輪，見圖1和圖2。

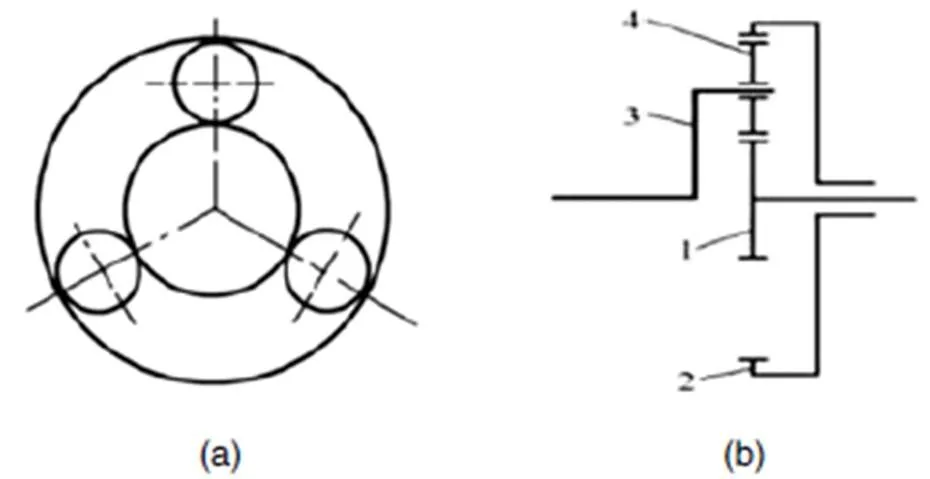
1—太陽輪；2—齒圈；3—行星架；4—行星輪。

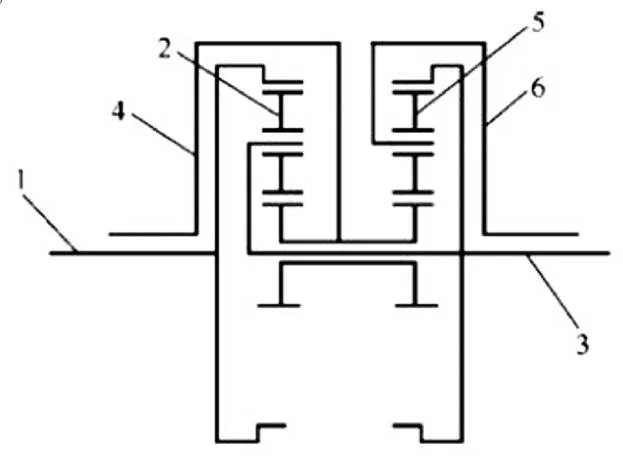
行星輪結構比較有代表性的組合方式有辛普森式和拉維納式行星齒輪機構[3]。辛普森式行星齒輪機構是由兩個簡單的單行星輪系結構組合而成，它分為六部分，分別為前齒圈、前行星架、前行星架和后齒圈組件、前后太陽輪組件、后行星輪、后行星齒輪架，見圖3。拉維納式行星齒輪機構是由一個單行星輪系和一個雙行星輪系組合而成，它也是分為六部分，分別為前太陽輪、后太陽輪、行星架、短行星輪、長行星輪、內齒圈，見圖4。

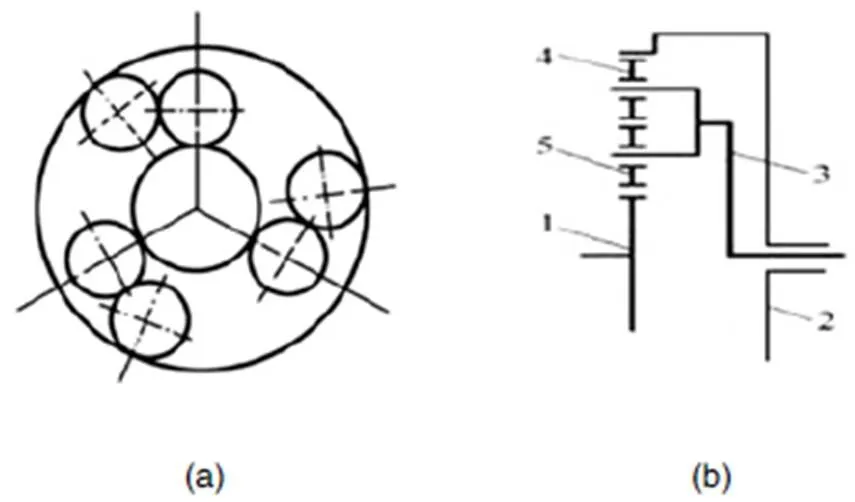
1—太陽輪；2—齒圈；3—行星架；4—外行星輪；5—內行星輪。

1—前齒圈；2—前行星架；3—前行星架和后齒圈組件；4—前后太陽輪組件； 5—后行星輪；6—后行星齒輪架。

1—前太陽輪；2—后太陽輪；3—行星架；4—短行星輪；5—長行星輪；6—內齒圈。

本文主要的研究對象為單雙行星輪系以及由單雙行星輪系組合形成的拉維納式行星齒輪機構。

1 特性方程

行星輪速比計算常采用機構轉化法：假設給整個輪系加上一個與行星架的轉速大小相等，轉向相反的附加轉速“?n”。根據相對運動關系，此時整個輪系中各原件間的相對運動關系并不會發生變化，但此時行星輪架轉速為零，即原來運動的行星輪架轉化為靜止，這樣原來的行星輪系就轉化為一個定軸輪系。對于此轉化機構的速比，則可以按定軸輪系的速比計算方式進行計算，轉化機構速比計算公式為：

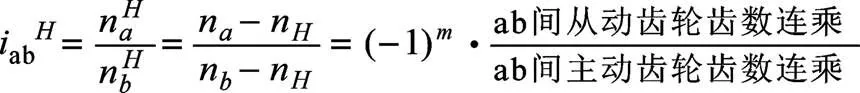
其中：ab表示H件固定主動件對從動件的傳動比；n=n?n表示相對的轉速；n=n?n表示相對的轉速；表示外嚙合次數，“?”負號表示ab轉速方向相反。

上式應用于單雙行星輪結構：

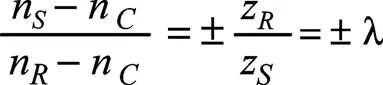
對于單行星，一對外嚙合齒輪，前取負號，得：

n+λn(1)= 0 （3）

對于雙行星，兩對外嚙合齒輪，前取正號，得：

nλn+(1)= 0 （4）

（3）式和（4）式稱為行星排轉速特性方程[4]，其中：

S表示太陽輪，C表示行星架，R表示外齒圈。

為齒圈齒數與太陽輪齒數比，稱為行星排特性參數：（=Z/Z）。

自動變速器內部結構往往由多個行星輪系組成，利用上式（3）和（4）列轉速特性方程組，就可以求得輸出元件的轉速，從而確定特定擋位的速比，下面舉例說明，見圖5：

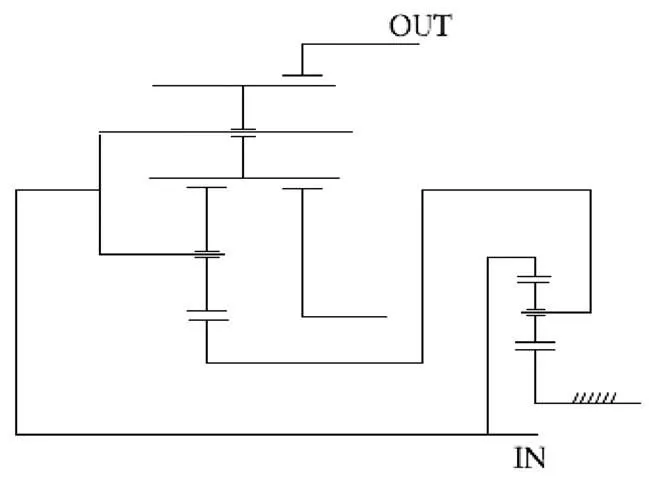
圖5 愛信6AT自動變速器 4擋時結構簡圖

從上圖可知，愛信6AT內部由一個單行星排和拉維納結構組成，當處于4擋時，輸入軸、單行星排外齒圈、拉維納行星架三者轉速相等，單行星排行星架與拉維納前太陽輪轉速相等，單行星排太陽輪固定轉速為0，拉維納后太陽輪空轉，拉維納外齒圈為輸出元件，假設輸入轉速為1個單位，求輸出速比，列轉速方程組：

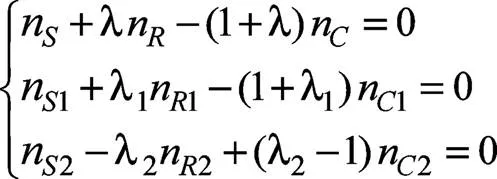
上式中：S、R、C為單行星排元件；1、1、1為拉維納中單行星排元件；2、R2、C2為拉維納中雙行星排元件。

解（5）方程組得：

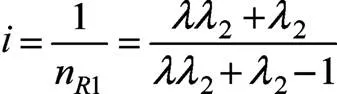
2 圖形法

利用（5）方程組求速比較繁瑣且易出錯，下面介紹一種更簡易的方法，圖形法。

由式（3）得：

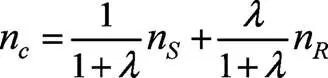
由式（4）得：

觀察式（7）可知，n，n前系數和為1，根據幾何知識一條線段被一個點分成兩段，每條線段所占總線段的比例加在一起和為1。利用這一特性就可以用圖形法來計算速比，首先做任意梯形如圖6：

圖6 任意梯形

其中：=，=，=，=，=，由幾何知識可得：

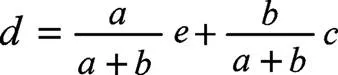
觀察式（9）可知，和前面系數和為1，若我們令梯形中=1，=，= n，= n帶入（9）式則可得到結果：

與式（7）結果一致并且可以得到圖7：

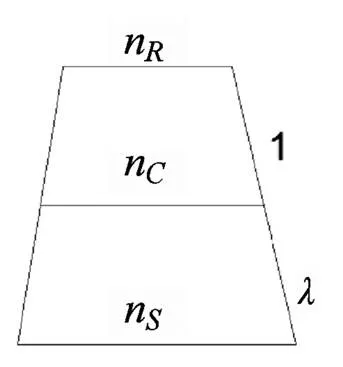
圖7 單行星輪系速比簡圖

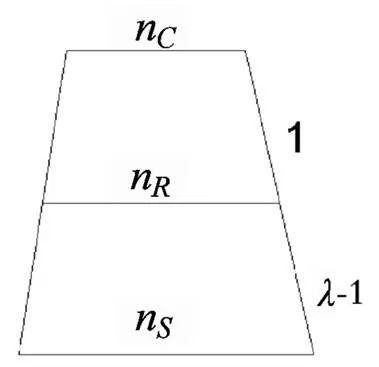
圖8 雙行星輪系速比簡圖

所以只要我們知道單行星輪中三元件中任意兩個元件的轉速，就可以根據圖7快速計算出第三個元件轉速，從而求得速比。

同理，對于雙行星輪結構，根據（8）式及圖6，令圖6中=1，=1，= n，= n，則可得到結果：

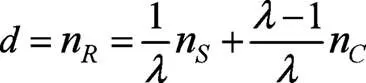
與式（8）結果一致并且可以得到圖8。

依據圖7和圖8這樣簡易的圖形，只要我們知道行星排三元件中任意兩元件的轉速，就可以快速求出第三個元件的轉速。

使用圖形法對圖5 愛信6AT 4擋速比進行求解，依然假設輸入轉速為1個單位，已知邊界條件有：n=0，n= n1n21，n= n2，n1 n2，求。為了更加直觀，將單行星排以及拉維納結構的梯形圖畫在一張圖里，如圖9：

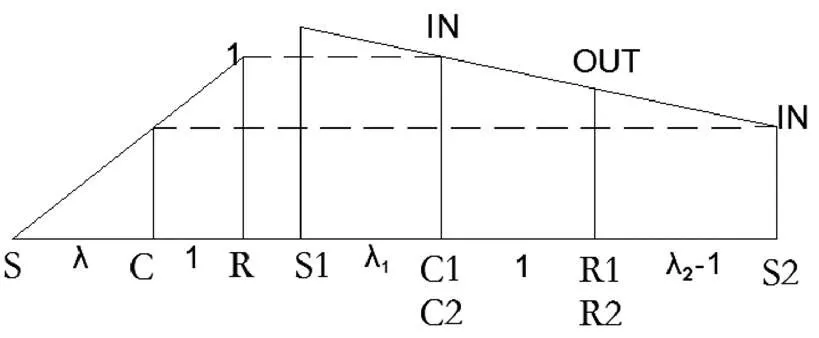
圖9 愛信6AT 4擋速比簡圖

根據幾何知識求得：

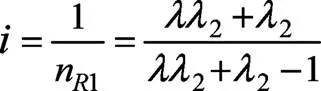
與列特性方程組求得結果（6）一致，可見圖形法計算速比更加直觀和準確。

3 結論

目前汽車行業普遍裝用自動變速器，而汽車自動變速器中以行星輪系為多，一般行星輪系都可以使用單行星輪系、雙行星輪系組合得來，以上應用特性方程求速比以及圖形法求速比的方法，能夠方便并且高效地為初學者提供一種快速分析行星輪系的途徑。

由于作者水平和經驗等原因，文中難免有不足之處，懇切希望讀者提出寶貴的完善意見。

[1] 陳家瑞.汽車構造[M].北京:人民交通出版社,2005.

[2] 齒輪手冊編委會.齒輪手冊[M].北京:機械工業出版社.2004,02.

[3] 黃宗益.現代轎車自動變速器原理和設計[M].上海:同濟大學出版社,2006.

[4] 李巍.自動變速器行星齒輪系統傳動原理[J].汽車維修,2004(4):60.

Combination of Number and Shape to Derive the Speed Ratio of Automatic Transmission

FENG Yongjun, GUAN Wei, TANG Liang, YUAN Xiaoxing, WANG Mo

（Harbin Dongan Automotive Engine Manufacture Co., Ltd., Technology Center, Heilongjiang Harbin 150000）

This article derives the characteristic equation of planetary gear train. The speed ratio of automatic transmission is calculated by the characteristic equation. In order to improve efficiency, a graphic method is derived to calculate the speed ratio of automatic transmission.

Automatic transmission[1]; Planetary gear train; Characteristic equation; Simpson planetary gear train; Ravigneaux planetary gear train

U463.212

A

1671-7988(2021)23-207-03

U463.212

A

1671-7988(2021)23-207-03

10.16638/j.cnki.1671-7988.2021.023.057

馮詠軍，就職于哈爾濱東安汽車發動機制造有限公司技術中心。