基于ARM的時(shí)變頻率測(cè)量算法設(shè)計(jì)

黨存祿，陳國(guó)國(guó)

（蘭州理工大學(xué) 電氣工程與信息工程學(xué)院，蘭州 730050）

國(guó)家規(guī)范對(duì)電力系統(tǒng)的頻率有著嚴(yán)格的要求，一般情況下頻率的偏差值為±0.2 Hz，它反映的是系統(tǒng)有功功率的平衡[1]。風(fēng)力發(fā)電和光伏發(fā)電的裝機(jī)容量越來(lái)越大，但是在這些新型能源系統(tǒng)中，頻率是不穩(wěn)定的，是隨著時(shí)間不斷變化的[2]。例如：負(fù)載波動(dòng)引起的有功功率不平衡，系統(tǒng)發(fā)生各種故障時(shí)，也會(huì)引起有功功率的不平衡。波動(dòng)的頻率不僅會(huì)影響到其測(cè)量的準(zhǔn)確性，而且有可能會(huì)使低頻減載裝置誤動(dòng)作或拒動(dòng)[3]。

在新能源系統(tǒng)中，頻率的測(cè)量主要由嵌入式微機(jī)系統(tǒng)來(lái)實(shí)現(xiàn)[4]。隨著科學(xué)技術(shù)的發(fā)展，新能源系統(tǒng)中各種自動(dòng)裝置對(duì)系統(tǒng)頻率的測(cè)量精度要求日趨嚴(yán)格[5]。當(dāng)前，離散傅里葉變換（DFT）、快速傅里葉變換（FFT）以及過(guò)零點(diǎn)測(cè)頻算法是嵌入式裝置中普遍使用的軟件測(cè)頻算法[6]。其中DFT 測(cè)頻算法當(dāng)采樣點(diǎn)數(shù)比較少時(shí)，會(huì)發(fā)生頻譜泄漏和柵欄效應(yīng)[7]，并且高次諧波對(duì)其影響很大，對(duì)以上的問(wèn)題后期進(jìn)行了各種各樣的改進(jìn)算法，其中加窗函數(shù)修正的DFT 測(cè)頻算法[8]存在主要的問(wèn)題是它的實(shí)時(shí)性達(dá)不到預(yù)計(jì)的要求；文獻(xiàn)[9]結(jié)合插值和迭代的優(yōu)點(diǎn)得到的DFT測(cè)頻算法計(jì)算復(fù)雜，反應(yīng)周期長(zhǎng)，不利于應(yīng)用到嵌入式裝置中。

基于頻率的變化率，本文提出了時(shí)變頻率測(cè)量算法，解決了頻率隨時(shí)間變化時(shí)，現(xiàn)有的測(cè)頻方法精度不高、誤差大、計(jì)算復(fù)雜等問(wèn)題。首先把原始的信號(hào)送入濾波器進(jìn)行濾波，濾除信號(hào)中所含的高次諧波、直流分量和噪聲；然后在每一段小區(qū)間內(nèi)對(duì)濾波后的信號(hào)采用過(guò)零點(diǎn)檢測(cè)算法[10]進(jìn)行頻率值的計(jì)算，將所得到的頻率值作為最小二乘非線性曲線擬合的迭代初值，在每一段小區(qū)間內(nèi)進(jìn)行正弦曲線擬合；最后對(duì)擬合后的曲線以調(diào)整采樣頻率的方式對(duì)其進(jìn)行二次采樣，將所得到的二次采樣數(shù)據(jù)進(jìn)行動(dòng)態(tài)頻率測(cè)量算法計(jì)算頻率，解決現(xiàn)有的算法計(jì)算量大、測(cè)量精度不高和占用內(nèi)存大等問(wèn)題。

1 頻率算法的基本原理

1.1 濾波器的設(shè)計(jì)

在實(shí)際運(yùn)行的電力系統(tǒng)中，信號(hào)波形往往不是標(biāo)準(zhǔn)的正弦曲線，其中夾雜著高次諧波、直流分量以及各種噪聲的復(fù)雜曲線[11]；系統(tǒng)正常運(yùn)行時(shí)，頻率在50 Hz 左右波動(dòng)，其中的諧波頻率也在隨著工頻不斷變化[12]，這就給頻率的準(zhǔn)確測(cè)量帶來(lái)了很大的測(cè)量誤差，因此需要設(shè)計(jì)濾波器。

本文采用基于巴特沃斯型帶通濾波器的設(shè)計(jì)[13]來(lái)濾除原始信號(hào)中所含的噪聲和諧波，文中主要設(shè)計(jì)參數(shù)：通帶范圍為45～55 Hz，通帶上限為60 Hz，通帶下限為40 Hz，通帶最大衰減為2 dB，阻帶最小衰減為15 dB。帶通濾波器頻率響應(yīng)如圖1所示。

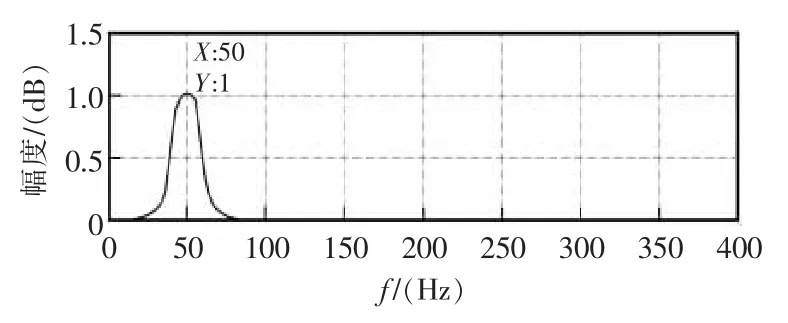
圖1 帶通濾波器頻率響應(yīng)Fig.1 Frequency response of bandwidth filter

分析圖1可得，當(dāng)信號(hào)經(jīng)過(guò)這款濾波器后，信號(hào)中的高次諧波分量和直流分量的衰減接近于0，最后只剩下50 Hz 附近的頻率可以通過(guò)濾波器。從而濾除掉原始信號(hào)中摻雜的直流分量和高次諧波分量，減小其對(duì)基波信號(hào)的干擾。

信號(hào)中不僅含有以上對(duì)信號(hào)的干擾項(xiàng)，而且含有各種隨機(jī)噪聲，帶通濾波器不可能把所有的干擾項(xiàng)全部濾除，經(jīng)過(guò)濾波器濾波后的信號(hào)中仍然含有一部分噪聲，這些未被濾除的噪聲很容易產(chǎn)生頻率泄漏，所以還要對(duì)信號(hào)的噪聲進(jìn)行處理。

1.2 基于列文伯格-馬夸爾特的最小二乘非線性曲線擬合原理

濾波后的信號(hào)中仍然含有部分的噪聲信號(hào)，這些噪聲信號(hào)很容易造成頻率的泄漏[14]，這就在很大程度上影響了現(xiàn)有測(cè)頻算法的測(cè)量精度。

本文運(yùn)用基于列文伯格-馬夸爾特的最小二乘非線性曲線擬合[15]方法對(duì)濾波后的信號(hào)進(jìn)行正弦曲線擬合。其基本原理為在濾波后信號(hào)的每段區(qū)間Vi中把濾波后的信號(hào)擬合成標(biāo)準(zhǔn)的正弦曲線Yi，表示為

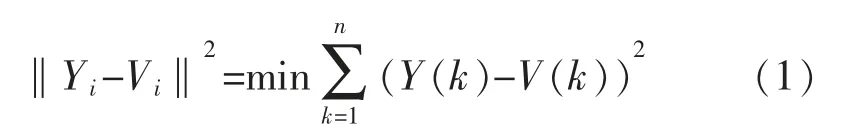
式中：Yi為第i 段的標(biāo)準(zhǔn)正弦擬合函數(shù)。

標(biāo)準(zhǔn)正弦擬合函數(shù)的各種參數(shù)，如相角、幅值和頻率的最優(yōu)值采用列文伯格-馬夸爾特方法來(lái)獲得，其中的初始值設(shè)為0.01。為了減小迭代次數(shù)，把迭代頻率的初始值設(shè)為過(guò)零檢測(cè)算法所得的頻率值，取0～π 中的任意值作為相角θ 的值。假如得到的參數(shù)值不在合理范圍值之內(nèi)，重新調(diào)整θ 的值對(duì)參數(shù)進(jìn)行優(yōu)化估計(jì)，直至參數(shù)值在合理范圍值之內(nèi)。最后對(duì)擬合后的正弦曲線進(jìn)行二次采樣，進(jìn)一步去除信號(hào)中的各種噪聲，從而提高頻率測(cè)量的算法精度。

1.3 頻率變化率與周期的關(guān)系

首先假設(shè)被測(cè)信號(hào)的幅值是Um，頻率為f，相角是φ（f，t），那么信號(hào)的表達(dá)式可以表示為

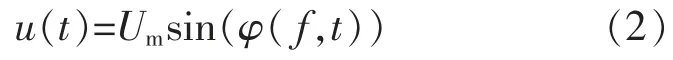
如果f 是隨時(shí)間變化的，那么f 的一階導(dǎo)數(shù)肯定不為零，則每一時(shí)刻的相角φ（f，t）可以表示為

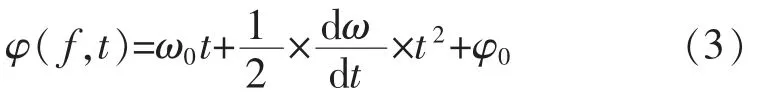
式中：ω=2π f 是角頻率；dω/dt 是角加速度；φ0是零時(shí)刻（t=0）的初始相角；ω0=2π f0是零時(shí)刻的初始角速度，f0為初始頻率。以緊鄰3 個(gè)過(guò)零點(diǎn)處的相位角為研究對(duì)象，如圖2所示。

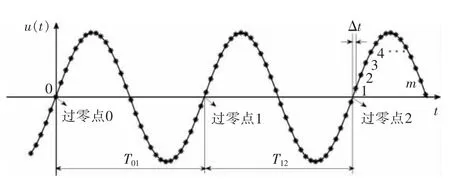
圖2 信號(hào)波形與過(guò)零點(diǎn)示意圖Fig.2 Signal waveform and zero crossing diagram

把過(guò)零點(diǎn)0 設(shè)置為起始點(diǎn)，則在t=0 處，相角φ0=0，頻率為f0。在過(guò)零點(diǎn)1 處，相角為2π，過(guò)零點(diǎn)2 處，相角為4π。

由式（3）得：

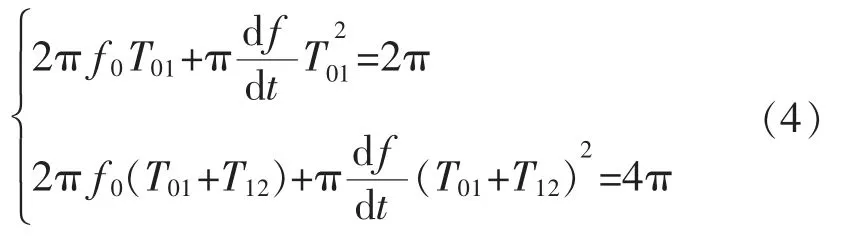
解得：

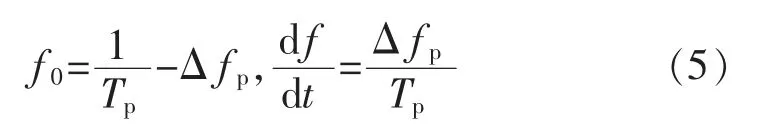
其中：

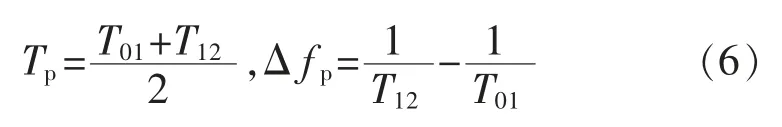
由式（5）和式（6）可以求出頻率的變化率d f/dt和過(guò)零點(diǎn)0 處的初始頻率f0。

根據(jù)以上所求得的結(jié)果可以計(jì)算出每一時(shí)刻的頻率。如圖2所示，假設(shè)過(guò)零點(diǎn)2 為最新的過(guò)零點(diǎn)，采樣點(diǎn)m 為當(dāng)前時(shí)刻的采樣點(diǎn)，過(guò)零點(diǎn)2 到當(dāng)前時(shí)刻之間的采樣值個(gè)數(shù)為m，因此當(dāng)前時(shí)刻的頻率為

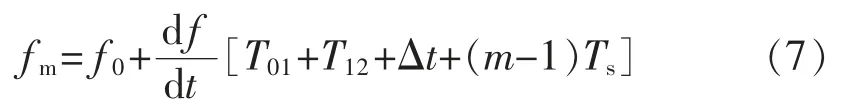
式中：Δt 是過(guò)零點(diǎn)2 與采樣點(diǎn)1 之間的時(shí)間；Ts為相鄰兩個(gè)采樣點(diǎn)之間的時(shí)間，即采樣時(shí)間間隔。

1.4 計(jì)算周期T

1.4.1 Δt 的計(jì)算

如圖2，在采樣的時(shí)候信號(hào)的過(guò)零點(diǎn)經(jīng)常并不一定與采樣點(diǎn)重合，要準(zhǔn)確求出周期T，則必須首先要求出過(guò)零點(diǎn)與過(guò)零點(diǎn)后的第一個(gè)采樣點(diǎn)之間的時(shí)間Δt。

對(duì)于信號(hào)的真正過(guò)零點(diǎn)是沒有辦法直接求解出來(lái)的，但是可以通過(guò)其他的方法近似求解，比如，可以把零點(diǎn)附近的波形看作是直線，然后采用相似三角行的方法來(lái)求解[16]。

為了解決相似三角形方法解得的過(guò)零點(diǎn)值精度不高的問(wèn)題，本文采用牛頓多項(xiàng)式[17]f（x）來(lái)逼近：

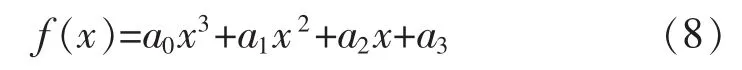
接下來(lái)就是計(jì)算式（8）的各項(xiàng)系數(shù)即a0，a1，a2，a3。

如圖3所示，依據(jù)式（8），從眾多的采樣點(diǎn)中取4 個(gè)采樣點(diǎn)，分別為過(guò)零點(diǎn)之后的第一個(gè)采樣點(diǎn)（tk，uk），過(guò)零點(diǎn)之前的三個(gè)采樣點(diǎn)（tk-1，uk-1）、（tk-2，uk-2）、（tk-3，uk-3）。根據(jù)這4 個(gè)采樣值可以建立向后差分表[18]，見表1。

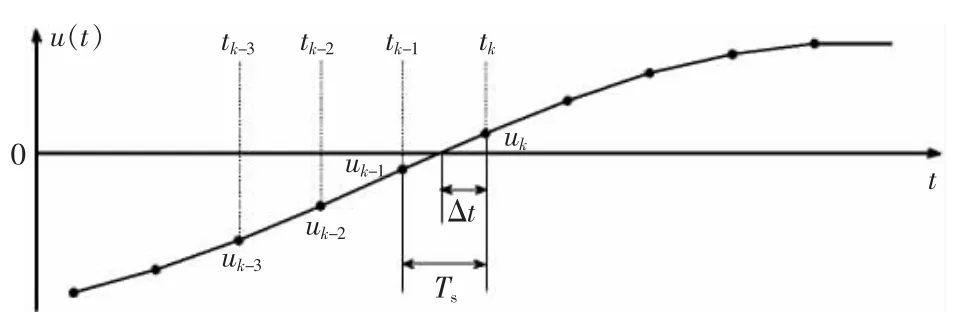
圖3 牛頓插值多項(xiàng)式示意圖Fig.3 Schematic diagram of Newton interpolation polynomial

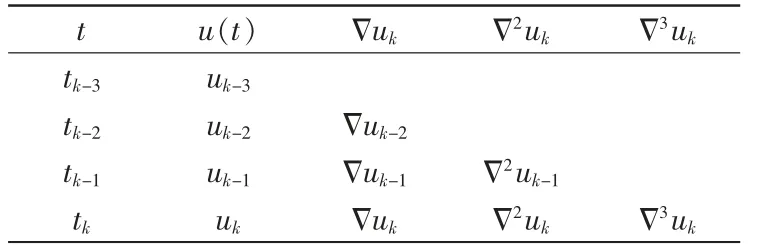
表1 牛頓向后差分表Tab.1 Newton backward difference table

其中，

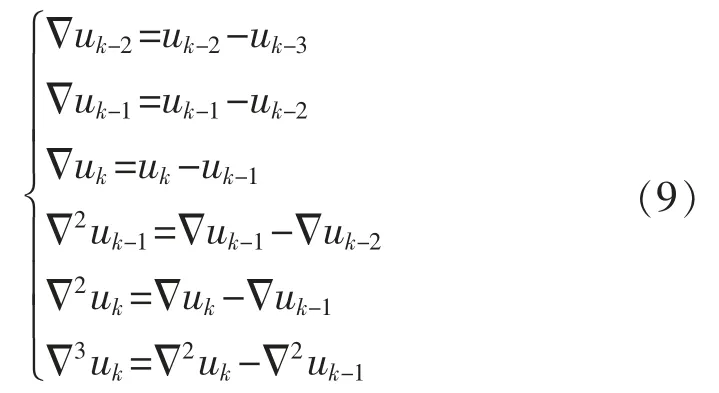
則，式（8）又可表示為

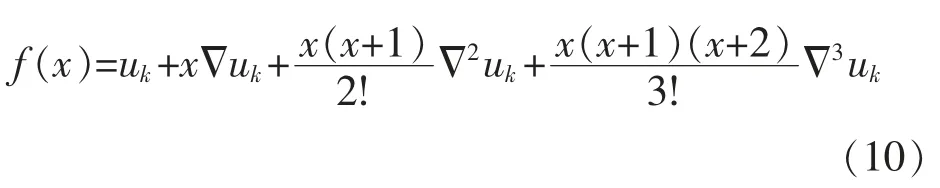
x 與Δt 之間的關(guān)系式為

從而求得式（8）的各項(xiàng)系數(shù)如下：

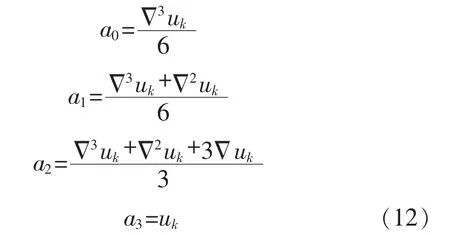
令f（x）=0，求解牛頓三次插值多項(xiàng)式過(guò)零點(diǎn)：

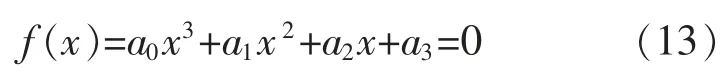
利用牛頓迭代方法求取f（x）=0 的根：

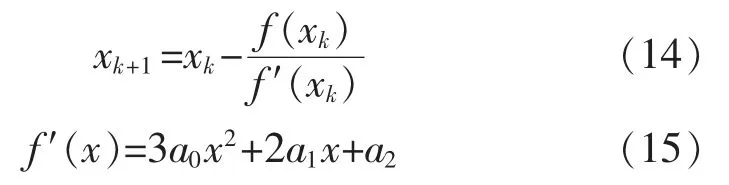
為了減少迭代的次數(shù)，首先采用相似三角形的方法求出迭代初值x0，見圖4所示，由相似三角形原理可得：

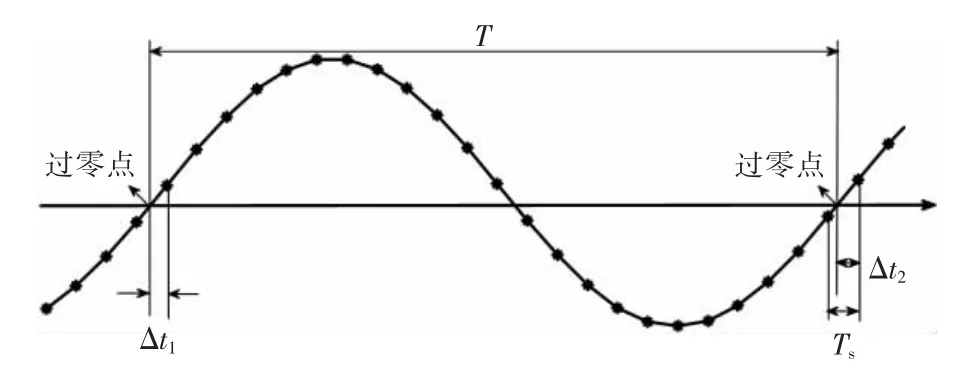
圖4 計(jì)算過(guò)零點(diǎn)時(shí)間方法示意圖Fig.4 Schematic diagram of method for calculating zero crossing time

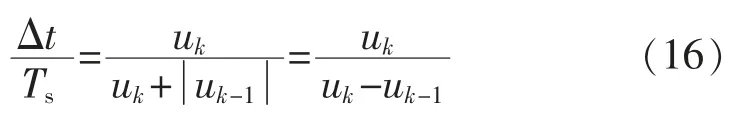
把Δt=-xTs代入式（16），可得：

所以迭代初值可以取為

當(dāng)?shù)冗_(dá)到所要求的精度時(shí)可以得到x 的值，最后計(jì)算出Δt=-xTs的值。

1.4.2 周期T 的計(jì)算

假設(shè)兩個(gè)緊鄰過(guò)零點(diǎn)之間的采樣點(diǎn)數(shù)為N，那么周期T 的計(jì)算公式為

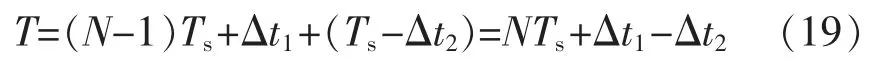
式中：Δt1和Δt2是過(guò)零點(diǎn)與過(guò)零點(diǎn)之后第一個(gè)采樣點(diǎn)之間的時(shí)間值。

2 算法的實(shí)現(xiàn)過(guò)程

（1）對(duì)過(guò)零點(diǎn)的判斷。當(dāng)uk*uk-1<0 時(shí)在uk與uk-1之間必有一個(gè)零點(diǎn)。

（2）按式（9）、式（12）計(jì)算擬合函數(shù)f（x）的系數(shù)a0～a3。

（3）求解過(guò)零點(diǎn)。首先依據(jù)式（18）算出迭代初值，再根據(jù)式（8）、式（13）、式（14）計(jì)算出過(guò)零點(diǎn)的近似解x 的值。

（4）當(dāng)前周期T 的計(jì)算。利用式（11）計(jì)算出Δt的值，再根據(jù)式（19）得到當(dāng)前周期T。

（5）最后計(jì)算采樣點(diǎn)處的頻率。采用式（7）計(jì)算頻率f。

3 算法的仿真

接下來(lái)分別對(duì)標(biāo)準(zhǔn)正弦波信號(hào)、含高次諧波和噪聲、頻率波動(dòng)情況下，對(duì)本文提出的算法進(jìn)行MATLAB 仿真，將仿真所得的結(jié)果與文獻(xiàn)[19]中的DFT 算法和文獻(xiàn)[20]中的過(guò)零點(diǎn)算法進(jìn)行比較，以驗(yàn)證本算法的優(yōu)越性。

3.1 標(biāo)準(zhǔn)正弦波

設(shè)標(biāo)準(zhǔn)正弦信號(hào)的數(shù)學(xué)模型為u（t）＝Umsin（2π ft+φ），頻率f 取45～54 之間，φ 角隨機(jī)選取。測(cè)量數(shù)據(jù)如表2所示。

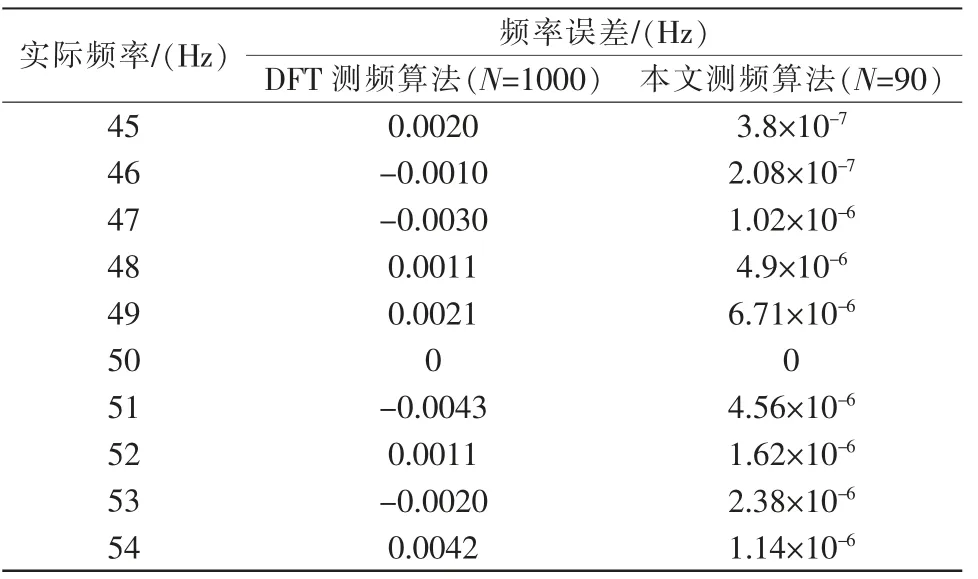
表2 標(biāo)準(zhǔn)正弦信號(hào)下的頻率誤差Tab.2 Frequency error under standard sinusoidal signal

3.2 含有噪聲和諧波

設(shè)含有噪聲和諧波信號(hào)的數(shù)學(xué)模型為

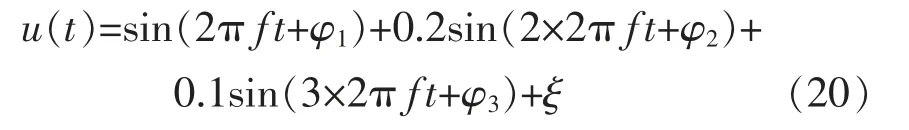
頻率f 取45～54 之間，φ 角隨機(jī)選取，ξ 為50 dB的白噪聲。測(cè)量數(shù)據(jù)如表3所示。

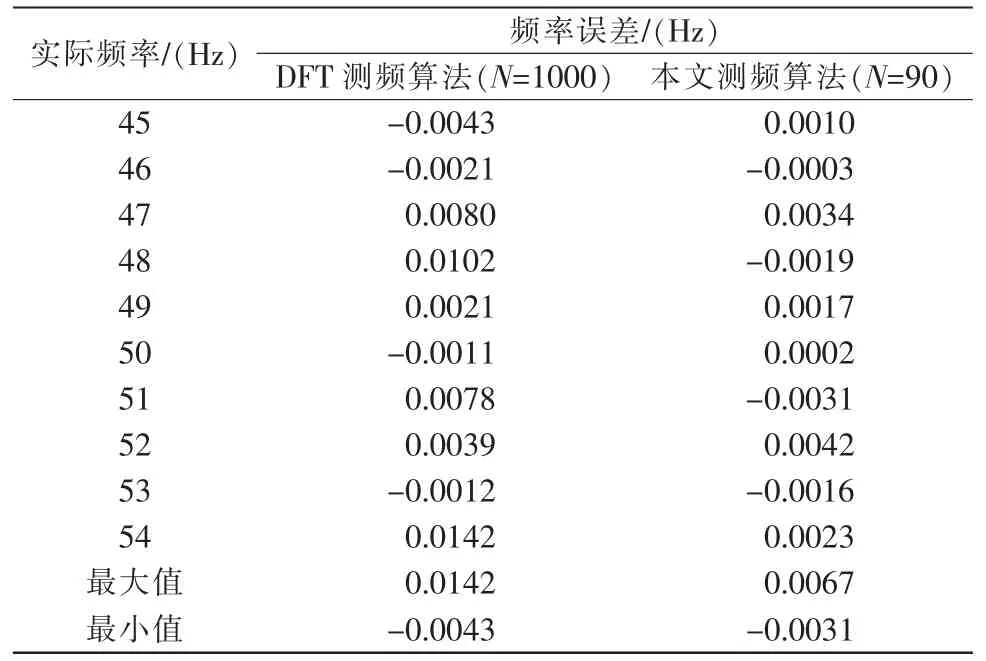
表3 含有噪聲和諧波信號(hào)下的頻率誤差Tab.3 Frequency error with noise and harmonic signal

3.3 頻率發(fā)生波動(dòng)

對(duì)發(fā)電機(jī)啟動(dòng)過(guò)程的頻率進(jìn)行模擬，取開始的頻率為35 Hz，初始相角為-10°，頻率變化率10，那么頻率和輸入電壓信號(hào)模型為

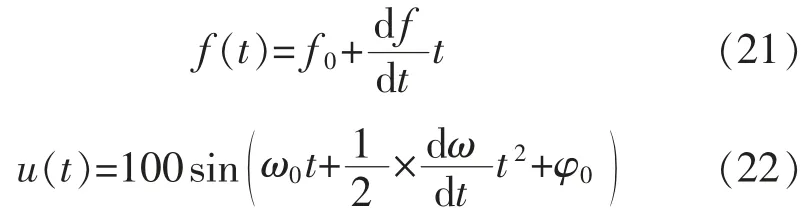
式中：ω0=2π f0；ω=2π f。測(cè)量數(shù)據(jù)如表4所示。

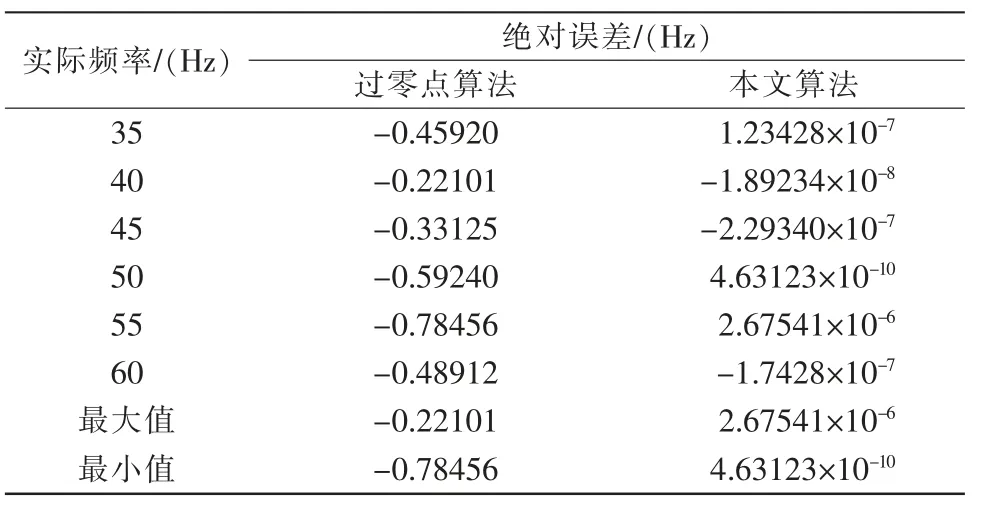
表4 頻率發(fā)生波動(dòng)時(shí)的頻率誤差Tab.4 Frequency error in case of frequency fluctuation

4 結(jié)語(yǔ)

在頻率發(fā)生波動(dòng)的條件下，以緊鄰兩個(gè)過(guò)零點(diǎn)之間的相位為依據(jù)，推算出了每一時(shí)刻頻率的數(shù)學(xué)表達(dá)式，從而提出了一種動(dòng)態(tài)頻率測(cè)量算法。本算法原理簡(jiǎn)單，實(shí)驗(yàn)仿真結(jié)果表明，本文算法在標(biāo)準(zhǔn)正弦信號(hào)下的頻率測(cè)量精度達(dá)到10-6Hz 級(jí)，在含有噪聲和諧波信號(hào)下的頻率測(cè)量精度可達(dá)10-3Hz 級(jí)，在頻率波動(dòng)下的頻率測(cè)量精度達(dá)到10-4Hz 級(jí)。

本文算法測(cè)量頻率的精度高、測(cè)量范圍廣、計(jì)算速度快、能有效地抵抗噪聲的干擾、在算法的準(zhǔn)確性和穩(wěn)定性方面有所提高，驗(yàn)證了本算法的可行性和有效性，解決了頻率波動(dòng)條件下，頻率測(cè)量精度不高、計(jì)算量大、占用嵌入式內(nèi)存大等問(wèn)題。