樹狀結構穩定承載力研究★

張 佳 寧

(遼寧工程技術大學土木工程學院，遼寧 阜新 123000)

1 概述

樹狀結構是德國建筑師Frei Otto于20世紀60年代基于仿生學概念提出的一種新型仿生結構形式，由于其良好的受力性能和美觀的結構外形在廣大的設計師和工程師中得到了廣泛的關注[1-7]。樹狀結構的傳力特點是將作用于結構頂部大范圍荷載沿著分支傳遞到最低級的分支，形成力流，逐級向下傳遞，最后匯聚到樹干，進而傳遞到地面上的一點。具有較高的結構效率[8]，從而被廣泛的應用于大型建筑中，如圖1所示。由于其美觀的結構外形，樹狀結構往往會成為地標性建筑[1,5]。

通過以樹狀結構作為支撐的火車站，機場等一些大跨度空間結構，支撐起來的屋頂結構的剛度要大大超過了樹狀結構自身的剛度。而且樹狀結構像自然界中的樹一樣向外擴展，直接的使自身所要承受的屋頂跨度和撓度減小，這樣就可以忽略屋頂結構產生的變形，假定屋頂剛度遠大于樹狀結構自身的剛度，基于這一假定，屋頂除了會向下傳遞荷載外，樹狀結構還會遭受到水平力的作用，而且樹狀結構自身受力比較均勻，當結構遭受的荷載或者外力到達一定值時，繼續施加荷載，結構的平衡狀態就會發生非常大的改變，這時所出現的現象就稱之為結構失穩或者結構屈曲。

在壓力的作用下，構件會出現失穩現象。所以，不論是整體結構還是單一的構件都需要考慮結構的穩定性問題，結構的穩定性是樹狀結構整體受力性能至關重要的因素。本文作者[9]已對樹狀結構的找形和優化進行了研究，但還未分析樹狀結構的失穩特征和穩定承載力[15]。本文針對于樹狀結構整體穩定性分析進行了系統的研究與闡述，其中主要分為兩部分：分別對樹狀結構找形前和找形后進行特征值屈曲分析和非線性屈曲分析，借此來驗證找形對于樹狀結構穩定性的影響。

2 模型建立

2.1 幾何參數

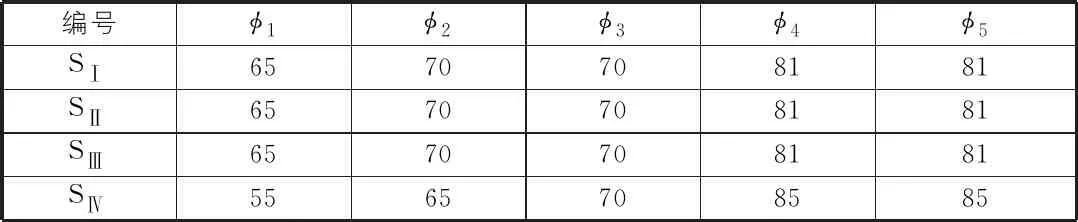
樹狀結構的組成部分可以根據它們相對于樹干位置進行分類，如圖2所示。從樹干上分出的支條被定義為一級分支，從一級分支構件分出被劃分為二級分支。屬于第i級分支的構件分出被劃分為第(i+1)級分支。樹狀結構連接節點可以根據每級分支的數量進行分類。不同連接類型的示意圖如圖3所示。各級分支長度如表1所示。其中Si表示樹狀結構類型。

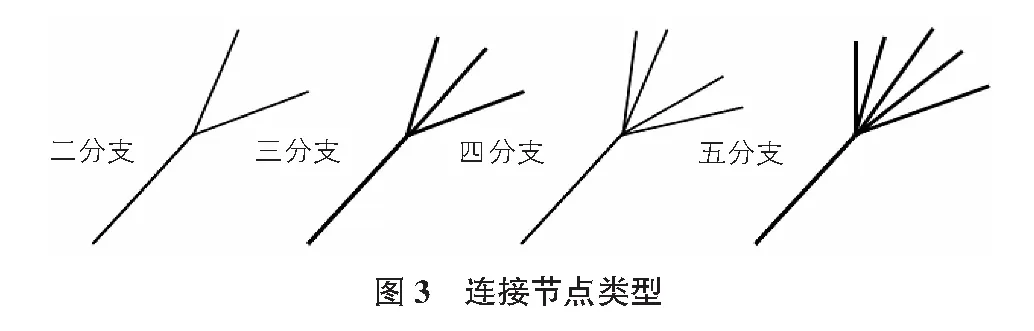
表1 不同情況下樹狀結構各級分支計算長度

m

如圖4所示為樹狀結構幾何參數，H0指樹狀結構樹干高度；Hi為第i級分支的高度;參數li指的是結構軸向上第i級分支的長度;參數Ф指的是一個分支與其更高級分支在軸向之間的夾角。各級樹狀結構分支夾角如表2所示。樹狀結構截面參數見表3。

表2 不同情況下樹狀結構各級分支計算角度

(°)

表3 樹狀結構截面參數

2.2 有限元模型及邊界條件

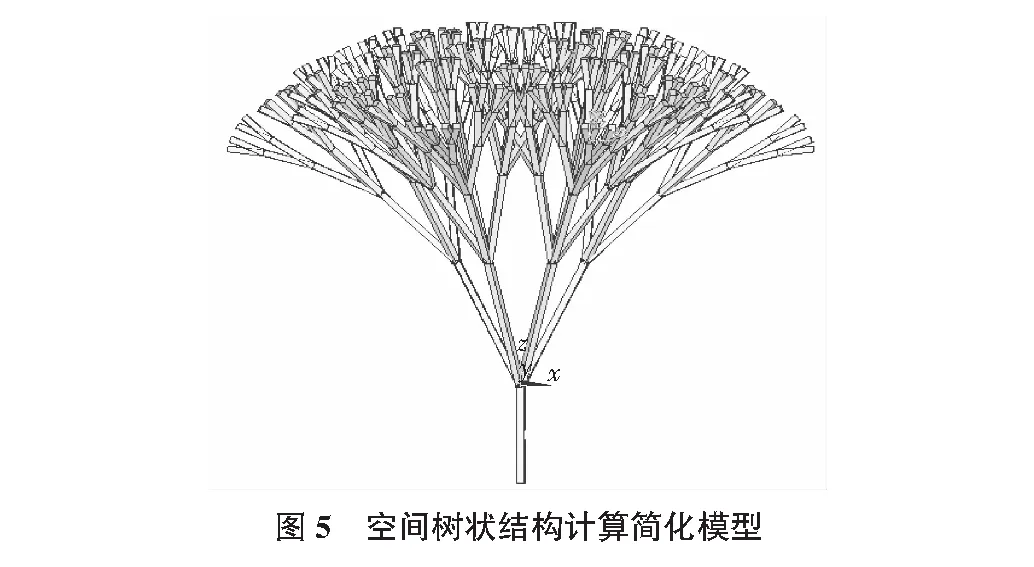
通過通用有限元軟件ANSYS建立樹狀結構，采用雙單元法[10-12]建立簡化模型，這種方法假定樹狀結構的每一個構件由兩個單元組成，即只有抗彎剛度的梁單元和沒有抗彎剛度的梁單元。桿單元的橫截面積遠大于梁單元，梁單元的抗彎剛度遠大于桿單元。在找形分析中，降低抗彎剛度以減小抗彎剛度的影響，因此梁單元可以更好的模擬絲線模型[13,14]。基于逆吊法[3-5]的基本思想在上方施加指定的載荷。如圖5所示為雙單元法建立的五級6-4-4-2-2樹狀結構簡化模型。

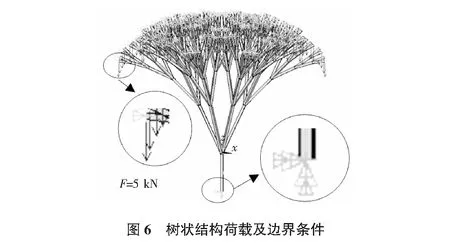
根據連接形式的不同，一般屋架結構與下部支撐結構采用剛接或者鉸接，本文在考慮樹狀結構的基本受力狀態，采用鉸接的形式，樹干底部采用固接形式，結構的頂層各個節點豎直方向施加5 kN的荷載，如圖6所示。

2.3 找形分析

趙中偉等[7]提出并利用雙單元法模擬樹狀結構。在本文中，上端在x和y方向上的平移度是固定的，樹干部位的平移程度均固定。在找形分析中只有水平坐標發生變化。在數值分析中，根據逆吊法的基本概念，向上施加指定載荷。然后進行模擬分析，得到節點位移。提取所有節點的水平位移，將水平位移與初始節點坐標求和得出新的節點坐標，通過新的節點坐標建立樹狀結構的雙單元數值模型，重新計算，通過樹狀結構找形分析的迭代程序，直到節點的最大位移小于允許誤差為止。這樣通過多次迭代，所有構件均只受軸力的作用，彎矩較小可以忽略不計。

3 非線性屈曲分析

為了進一步探討樹狀結構的結構缺陷和結構失穩機理，對樹狀結構進行非線性屈曲分析。其中考慮幾何非線性對于樹狀結構的整體穩定性能的影響。目前非線屈曲分析的應用已經很成熟了。

在固體力學的問題中，所有現象都是非線性的。然而在工程項目中遇見的很多工程問題，近似地使用線性理論來處理是簡單切實可行，并且符合工程中的精度要求。

結構的非線性分析問題可以分為三大類：幾何非線性問題，材料非線性問題，狀態非線性問題。一般來說，結構非線性問題并不是單純的某一類問題，可能需要同時考慮共同作用的非線性問題，其中包括三種非線性問題并存的情況，這些問題都可以用ANSYS來解決。

非線性方程一般采用Newton-Raphon方法，這是求解非線性方程的線性化方法，對于樹狀結構來說，應考慮的是幾何非線性問題，結構的平衡方程為：

[K({u})]{u}={F}

(1)

寫成NR法迭代公式為：

[KT({u}n)]{Δu}n+1={F}-{F}n

(2)

{u}n+1={u}n+{Δu}n+1

(3)

本節對樹狀結構進行非線性屈曲分析時，在進行非線性屈曲分析過程中，根據結構在特征值屈曲分析過程中得到的一階失穩模態施加初始缺陷。材料的非線性考慮使用理想狀態下的彈塑性模型。在進入求解狀態時，采用弧長法對樹狀結構進行非線性整體分析。

3.1 樹狀結構找形前非線性分析

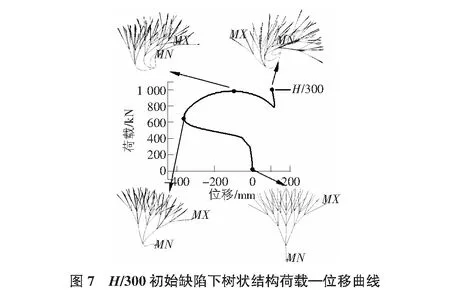
為了探究在樹狀結構非線性屈曲分析找形對于樹狀結構穩定性的影響，先對于5-6-4-4-2-2分支形式的樹狀結構進行非線性分析，選取施加不同程度的初始缺陷大小，研究在不同參數狀態下的樹狀結構失穩形態和失穩過程。如圖7所示為首先施加H/300的初始缺陷。

如圖7所示，選取樹干部位與一級分支連接處的7031節點，給出了在H/300的初始缺陷下樹狀結構的荷載—位移曲線，可以清晰的看出，在幾何非線性條件下，樹狀結構的荷載—位移曲線非常圓滑，在結構失穩變形后，尤其是發生大變形時，樹狀結構在一定范圍內還可以承擔荷載，在結構達到負向的最大位移后，又趨向正向位移，此時樹干受力形式從受壓失穩轉向受拉失穩。同時，從圖中可以清晰的發現，結構失穩已經從樹干失穩轉向了樹狀結構外部高級分支的失穩。通過樹狀結構失穩變形圖，可以發現，在考慮幾何非線性條件下樹狀結構的失穩破壞形式和特征值屈曲分析中一階模態失穩破壞比較相似，最大位移處也發生在最高級分支頂部邊緣處。

3.2 樹狀結構找形后非線性分析

對樹狀結構進行找形，探究找形對樹狀結構非線性屈曲分析的影響，在找形后施加相同條件的初始缺陷，研究找形后樹狀結構失穩形態和失穩過程。施加H/300的初始缺陷。

如圖8可以清晰的看到在H/300的初始缺陷下找形后樹狀結構的荷載—位移曲線，在幾何非線性條件下，樹狀結構的荷載—位移曲線非常圓滑，在結構失穩變形后，尤其是發生大變形時，樹狀結構在一定范圍內還可以承擔荷載，在結構達到負向的最大位移后，樹狀結構從局部受壓轉向局部受拉。可以明顯看出樹狀結構樹干部位變形明顯，和找形前進行對比，分支部位變形較小。

通過樹狀結構失穩變形圖，可以得出一階模態失穩破壞變形圖，數據表明，樹狀結構的最大位移處發生在樹根部位與最高級分支頂部邊緣處。

通過對比研究，結果表明，樹狀結構的非線性失穩模態，一般不受初始缺陷的影響。

4 結語

本文對找形前后的樹狀結構進行了穩定特性分析。以雙單元法建立的樹狀結構數值模型為基礎，提出了樹狀結構的非線性屈曲分析。

1)結果顯示找形對于樹狀結構的穩定性并沒有太大的影響，在找形前后并沒有明顯改變樹狀結構失穩形態。在給定荷載下，大跨度樹狀結構的各個分支因軸力或者軸力與彎矩的共同作用，結構發生的失穩位移更加明顯。

2)基于幾何非線性對樹狀結構的整體穩定性進行了非線性分析。找形前樹狀結構受初始缺陷影響不大，找形后樹狀結構在失穩后仍能在一定范圍內承擔荷載。

3)通過樹狀結構整體穩定性分析發現，樹狀結構受樹干，一級分支以及結構跨度對結構的穩定性起著明顯的作用，設計時可以通過增加樹干和一級分支剛度，減小結構跨度等方法來提高樹狀結構穩定性。