二維耦合諧振子的非對(duì)易能譜

茍立丹

(長(zhǎng)春理工大學(xué)物理學(xué)院, 長(zhǎng)春 130022)

(2021 年1 月14 日收到; 2021 年6 月9 日收到修改稿)

1 引 言

非對(duì)易空間的概念很早就被提出了[1], 但最初并沒(méi)有引起人們的重視. 后來(lái)由于弦理論的發(fā)展[2],非對(duì)易研究重新受到了人們的關(guān)注. 研究人員開始探索一些領(lǐng)域中的非對(duì)易效應(yīng), 例如量子引力[3,4]、凝聚態(tài)物理[5]等. 很多問(wèn)題被納入到了非對(duì)易空間中進(jìn)行研究[6-8], 例如諧振子[9]、氫原子[10]、朗道能級(jí)[9,11]等. 通常研究非對(duì)易空間量子系統(tǒng)的方法是將非對(duì)易算符通過(guò)映射的方法投影到對(duì)易空間, 使得算符滿足標(biāo)準(zhǔn)的海森伯代數(shù), 從而解決非對(duì)易問(wèn)題. 2008 年范洪義等[12]把不變本征算符方法(invariant eigen-operator method, IEO)引入到非對(duì)易范疇, 用于求解非對(duì)易空間諧振子哈密頓量的能譜. 該方法是在海森伯思想和薛定諤算符的基礎(chǔ)上提出的一種求解量子系統(tǒng)能譜的方法[13,14], 已經(jīng)在物理學(xué)的很多領(lǐng)域有著廣泛的應(yīng)用, 如固體物理[15,16]、介觀物理[17,18]、二次型哈密頓量[19]等. 研究表明IEO 方法對(duì)于處理非對(duì)易空間諧振子的能譜問(wèn)題是比較有效的. 目前已有學(xué)者用IEO 方法研究過(guò)非對(duì)易相空間中任意維諧振子[20]、雙模耦合諧振子[21]、三模耦合諧振子能譜[22].

耦合諧振子模型是量子理論、固體物理、原子分子物理等領(lǐng)域中的基礎(chǔ)模型, 對(duì)于研究多體問(wèn)題和關(guān)聯(lián)系統(tǒng)的相互作用具有重要的理論意義和實(shí)際價(jià)值. 例如: 晶體中原子排列成有序的結(jié)構(gòu), 原子與原子之間的相互作用可以用耦合諧振子模型進(jìn)行模擬, 耦合參數(shù)可以描述相互作用強(qiáng)度. 此外,還有很多的物理問(wèn)題都可以簡(jiǎn)化到耦合諧振子模型, 因此研究非對(duì)易空間中的耦合諧振子能譜特性是很有意義的[23-25]. 文獻(xiàn)[26]利用坐標(biāo)變換將非對(duì)易問(wèn)題變?yōu)閷?duì)易問(wèn)題, 然后用通常的量子力學(xué)方法求解. 文獻(xiàn)[27]介紹了變形量子化方法, 即通過(guò)引入時(shí)間演化函數(shù)和魏格納函數(shù)進(jìn)行求解.

目前的研究結(jié)果普遍存在兩方面的問(wèn)題, 一是對(duì)于非對(duì)易空間, 只考慮了坐標(biāo)和坐標(biāo)不對(duì)易的情形, 而忽視了動(dòng)量和動(dòng)量的不對(duì)易, 以及兩者同時(shí)存在不對(duì)易的情形[26]; 二是耦合諧振子模型的哈密頓量只含有某一類耦合項(xiàng), 并沒(méi)有討論同時(shí)包含多種耦合項(xiàng)的哈密量的本征問(wèn)題[21,22,26,27].

在非對(duì)易的理論框架下出現(xiàn)了很多新的問(wèn)題,由于坐標(biāo)算符之間的不對(duì)易和動(dòng)量算符之間的不對(duì)易, 所以求解耦合諧振子的能譜并非易事. 而IEO方法源于海森伯方程, 無(wú)須涉及系統(tǒng)的具體量子態(tài), 只關(guān)注能級(jí)間隙, 避免了哈密頓量的對(duì)角化,可以比較容易地解決一些問(wèn)題. 因此本文嘗試用IEO 方法研究坐標(biāo)和動(dòng)量同時(shí)存在不對(duì)易的非對(duì)易相空間中二維耦合諧振子的量子特性. 用該方法可以較方便地得出同時(shí)包含坐標(biāo)坐標(biāo)耦合、動(dòng)量動(dòng)量耦合及坐標(biāo)動(dòng)量交叉耦合項(xiàng)的哈密頓量的能級(jí)差, 進(jìn)而得到體系的非對(duì)易能譜. 然后詳細(xì)分析了非對(duì)易參數(shù)和耦合參數(shù)對(duì)于非對(duì)易能級(jí)的具體影響, 得到了一些有意義的結(jié)果.

2 不變本征算符方法

量子力學(xué)中海森伯運(yùn)動(dòng)方程為(采用自然單位制 ?=1 )

引入不變本征算符O, 使其滿足方程

由(3)式可知λ=Eb?Ea, 因此,λ就是系統(tǒng)的能級(jí)差 ΔE.

3 二維耦合諧振子的非對(duì)易能譜

在一般的對(duì)易空間中, 坐標(biāo)算符xi和動(dòng)量算符pi滿足海森伯代數(shù)關(guān)系:

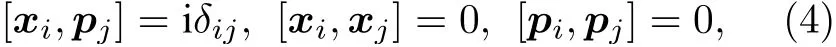
其中i,j=1,2 .在非對(duì)易相空間中, 坐標(biāo)算符Xi和動(dòng)量算符Pi滿足以下關(guān)系:

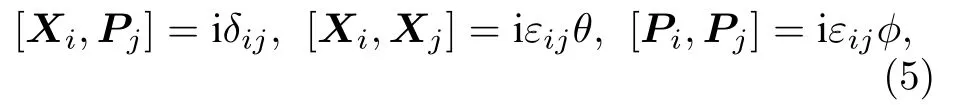
其中,εij是反對(duì)稱張量,θ和?是非對(duì)易參數(shù). 非對(duì)易相空間中的坐標(biāo)和動(dòng)量是缺乏對(duì)稱性的.

文獻(xiàn)[26, 27]研究的二維耦合諧振子模型的哈密頓量?jī)H含有坐標(biāo)耦合項(xiàng), 為了使討論更具有一般性, 本文設(shè)二維耦合諧振子的哈密頓量是

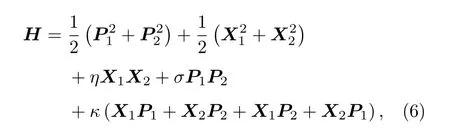
其中,η是坐標(biāo)坐標(biāo)耦合參數(shù),σ是動(dòng)量動(dòng)量耦合參數(shù),κ是坐標(biāo)動(dòng)量交叉耦合參數(shù), 這些耦合參數(shù)可以表示相互作用的強(qiáng)度. 哈密頓量H包含了所有的可能的耦合項(xiàng), 可以作為二維耦合諧振子的一般模型. 通過(guò)(5)式得到

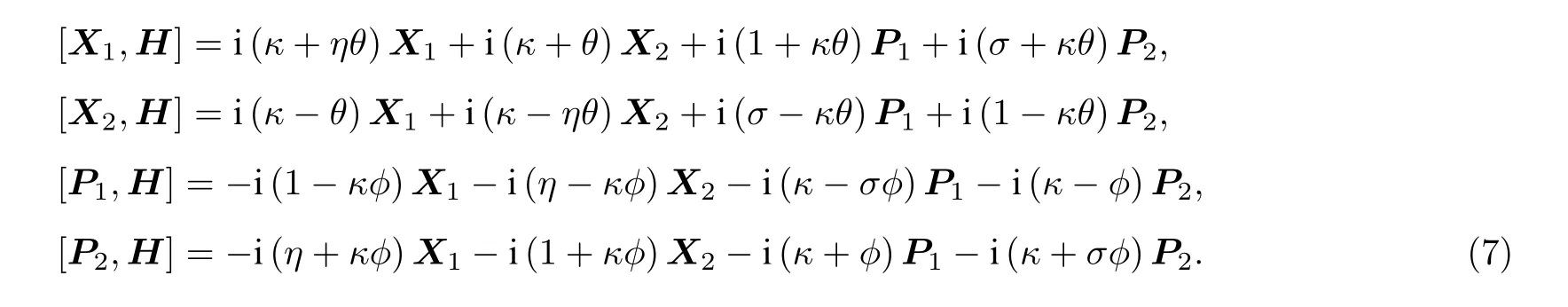
可以看出算符集合{X1,X2,P1,P2}在與H對(duì)易關(guān)系的運(yùn)算中是封閉的, 因此設(shè)不變本征算符為

其中,α,β,γ,ε是待定的系數(shù). 算符O滿足如下方程

將(6)式和(8)式代入(9)式解得

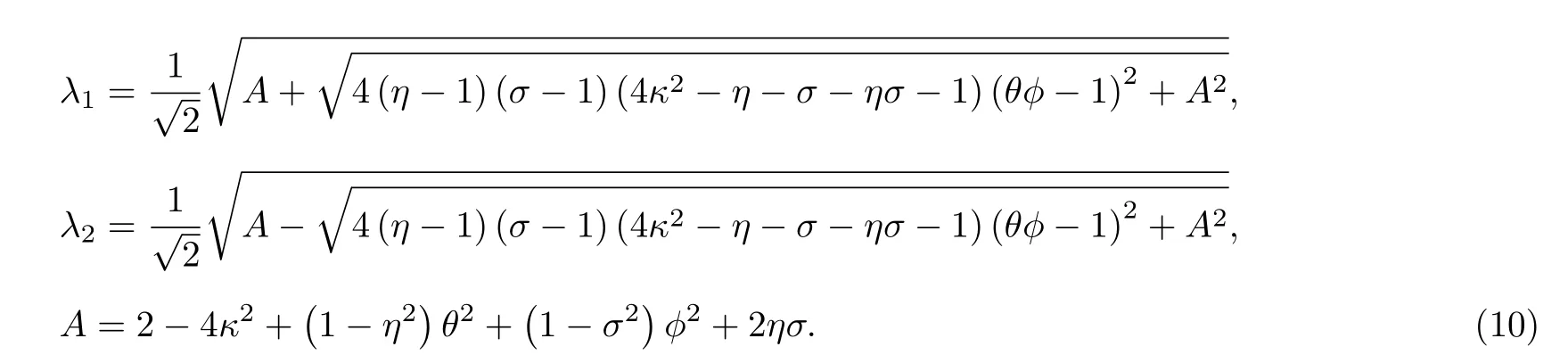
根據(jù)IEO 方法,λ1和λ2為系統(tǒng)的能級(jí)差 ΔE. 由此可以得到二維耦合諧振子的非對(duì)易能級(jí)為

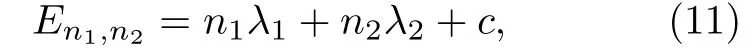
其中,n1,n2是量子數(shù), 且是非負(fù)整數(shù);c是常數(shù).我們所熟知的通常對(duì)易空間中二維諧振子的能級(jí)是En1,n2=n1+n2+1 , 且能級(jí)除基態(tài)外都是簡(jiǎn)并的. 考慮對(duì)(11)式取極限θ →0 ,? →0 , 并且忽略耦合項(xiàng)可以得到通常二維諧振子的能級(jí), 所以取c= 1.

4 討 論

假設(shè)所有耦合參數(shù)都為0, 則二維非耦合諧振子的非對(duì)易能級(jí)可以寫為

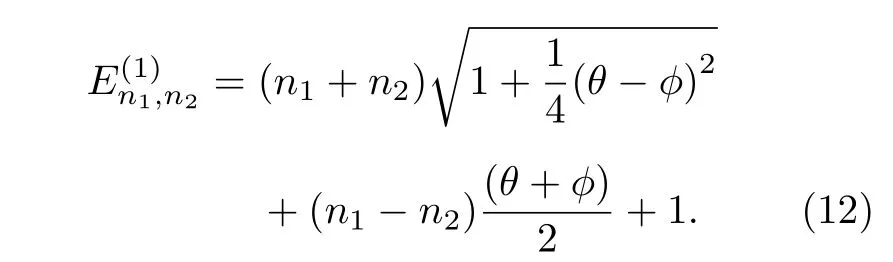
由(12)式可以看出二維非耦合諧振子的非對(duì)易能級(jí)是非簡(jiǎn)并的. 為了展示非對(duì)易性對(duì)該能級(jí)的影響, 我們舉一個(gè)具體的例子, 即當(dāng)n1+n2=2 時(shí),各個(gè)能級(jí)的值如表1 所示.

表1 能級(jí) 的值(n1+n2 = 2, η= σ = κ = 0)Table 1. Values of E (n1+n2 = 2, η = σ = κ = 0).

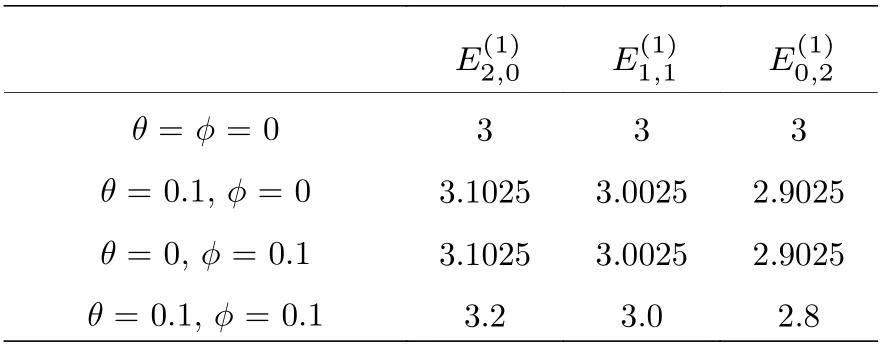
表1 能級(jí) 的值(n1+n2 = 2, η= σ = κ = 0)Table 1. Values of E (n1+n2 = 2, η = σ = κ = 0).

E(1)2,0E(1)1,1E(1)0,2 θ = φ = 0333 θ = 0.1, φ = 03.10253.00252.9025 θ = 0, φ = 0.13.10253.00252.9025 θ = 0.1, φ = 0.13.23.02.8

從表1 可以看到, 第2 行當(dāng)非對(duì)易參數(shù)θ和?都為0 時(shí), 能級(jí)是簡(jiǎn)并的, 這與通常對(duì)易空間中二維諧振子的能級(jí)情況是一致的. 而表中第3 至5 行當(dāng)參數(shù)θ和?不為0 時(shí), 能級(jí)會(huì)出現(xiàn)劈裂. 第3 行參數(shù)θ對(duì)能級(jí)的影響程度和第4 行參數(shù)?的影響程度是一樣的, 即以相同的數(shù)值破壞能級(jí)的簡(jiǎn)并. 第5 行中參數(shù)θ和?的同時(shí)作用會(huì)加大能級(jí)劈裂的程度. 這些結(jié)果表明雖然對(duì)易空間二維諧振子存在對(duì)稱性, 具體表現(xiàn)為能級(jí)的簡(jiǎn)并, 但是非對(duì)易性能夠破壞這種對(duì)稱性, 并產(chǎn)生了能級(jí)劈裂.

當(dāng)非對(duì)易參數(shù)θ和?都為0 時(shí), 二維耦合諧振子的能級(jí)可以寫為

為了展示耦合諧振子能級(jí)的變化, 仍以n1+n2=2時(shí)的能級(jí)為例, 具體能級(jí)值如表2 所示.

表2 說(shuō)明即使非對(duì)易參數(shù)θ和?為0, 但耦合參數(shù)η,σ和κ不為0, 能級(jí)也會(huì)出現(xiàn)劈裂, 即耦合項(xiàng)的加入同樣會(huì)破壞能級(jí)的對(duì)稱性, 使得能級(jí)變成非簡(jiǎn)并的. 表2 第2 至4 行表示系統(tǒng)只包含一類耦合項(xiàng)時(shí)能級(jí)的變化, 可以看出坐標(biāo)耦合參數(shù)η和動(dòng)量耦合參數(shù)σ對(duì)能級(jí)的影響程度是一樣的, 但是坐標(biāo)動(dòng)量交叉耦合參數(shù)κ對(duì)能級(jí)的影響小于η和σ.表2 第5 至7 行表示系統(tǒng)包含兩類耦合項(xiàng)時(shí)能級(jí)的變化. 其中第5 行是系統(tǒng)同時(shí)包含坐標(biāo)耦合和動(dòng)量耦合時(shí)的能級(jí), 與第2 至4 行比較可以發(fā)現(xiàn)當(dāng)系統(tǒng)同時(shí)包含兩個(gè)耦合項(xiàng)時(shí)能級(jí)劈裂的程度變大了.第6 行是系統(tǒng)同時(shí)包含坐標(biāo)耦合和坐標(biāo)動(dòng)量交叉耦合時(shí)的能級(jí), 與第5 行比較可以發(fā)現(xiàn)坐標(biāo)動(dòng)量交叉耦合項(xiàng)的出現(xiàn)使能級(jí)劈裂的程度變小了. 第7 行是系統(tǒng)同時(shí)包含動(dòng)量耦合和坐標(biāo)動(dòng)量交叉耦合時(shí)的能級(jí), 與第6 行的結(jié)果是一樣的. 表2 第8 行是系統(tǒng)同時(shí)包含坐標(biāo)耦合、動(dòng)量耦合和坐標(biāo)動(dòng)量交叉耦合時(shí)的能級(jí), 與第5 至7 行比較可以發(fā)現(xiàn)當(dāng)系統(tǒng)同時(shí)包含三類耦合項(xiàng)時(shí)能級(jí)劈裂的程度進(jìn)一步增大了.

表2 能級(jí) 的值(n1+n2 = 2, θ = φ = 0)Table 2. Values of E(n1+n2 = 2, θ = φ = 0).

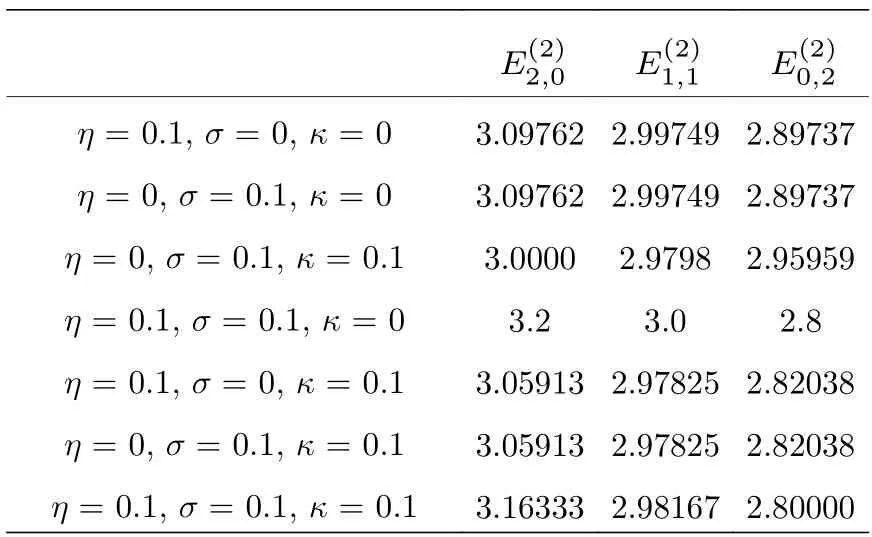
表2 能級(jí) 的值(n1+n2 = 2, θ = φ = 0)Table 2. Values of E(n1+n2 = 2, θ = φ = 0).

E(2)2,0E(2)1,1E(2)0,2 η = 0.1, σ = 0, κ = 03.09762 2.99749 2.89737 η = 0, σ = 0.1, κ = 03.09762 2.99749 2.89737 η = 0, σ = 0.1, κ = 0.13.0000 2.9798 2.95959 η = 0.1, σ = 0.1, κ = 03.23.02.8 η = 0.1, σ = 0, κ = 0.13.05913 2.97825 2.82038 η = 0, σ = 0.1, κ = 0.13.05913 2.97825 2.82038 η = 0.1, σ = 0.1, κ = 0.13.16333 2.98167 2.80000

能級(jí)En1,n2(n1+n2=2) 隨參數(shù)θ的變化情況如圖1 所示. 從圖1 可以看到,E2,0隨著θ的增加而增加.E1,1隨著θ的變化比較平緩, 總體趨勢(shì)是逐漸增加的.E0,2是隨著θ的增加先減小后增加.而且圖1中θ=1 的點(diǎn)是能級(jí)的最小值. 這是因?yàn)楫?dāng)θ?=1 時(shí)(11)式中的第2 項(xiàng)等于0. 另外, 當(dāng)θ取較大值時(shí), 能級(jí)E1,1和E2,0呈現(xiàn)出線性變化的趨勢(shì).能級(jí)En1,n2隨參數(shù)?的變化情況與圖1 相同, 這里不再贅述.

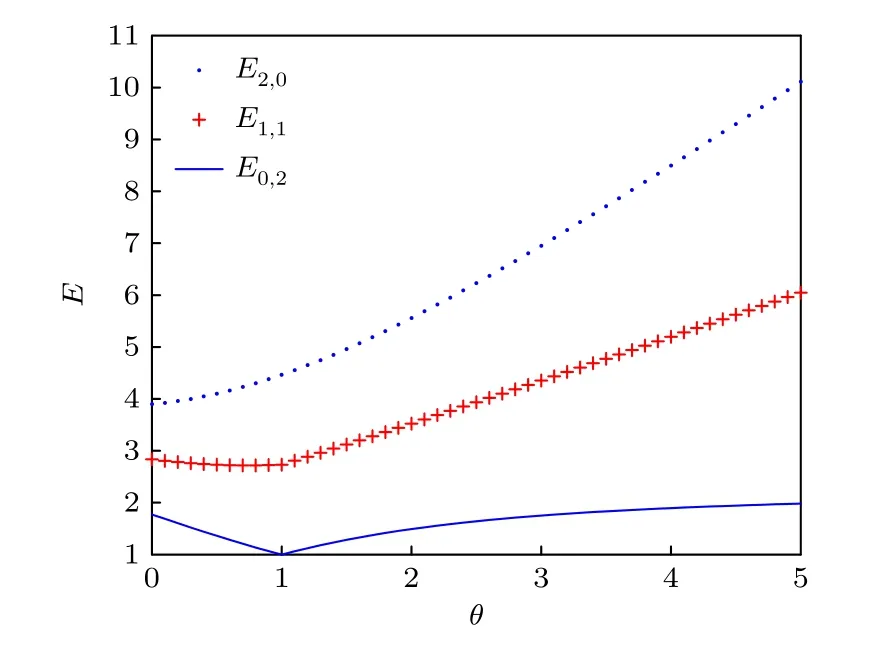
圖1 En1,n2 隨θ 的變化曲線(n1 + n2 = 2, φ = 1, η =0.5, σ = 0.5, κ = 0.5)Fig. 1. En1,n2 versus θ (n1 + n2 = 2, φ = 1, η = 0.5, σ =0.5, κ = 0.5).

5 結(jié) 論

本文構(gòu)造了同時(shí)包含坐標(biāo)坐標(biāo)、動(dòng)量動(dòng)量及坐標(biāo)動(dòng)量交叉的所有耦合項(xiàng)的二維耦合諧振子的模型, 并在非對(duì)易相空間中研究其能譜的特性. 首先,用IEO 方法計(jì)算得到了二維耦合諧振子非對(duì)易能譜的解析解. 從(10)式和(11)式可以看出, 系統(tǒng)能譜是與耦合參數(shù)和非對(duì)易參數(shù)有關(guān)的. 其次, 由于該解析解形式比較復(fù)雜, 所以對(duì)其進(jìn)行了分類討論. 以圖表的形式詳細(xì)分析了耦合參數(shù)和非對(duì)易參數(shù)對(duì)能譜的影響, 得到以下結(jié)果. 1)受到非對(duì)易參數(shù)的影響能級(jí)會(huì)出現(xiàn)劈裂. 一般對(duì)易空間中二維諧振子具有較高的對(duì)稱性, 表現(xiàn)在其能級(jí)除基態(tài)外是簡(jiǎn)并的. 然而, 非對(duì)易性的出現(xiàn)破壞了這種對(duì)稱性,使得能級(jí)出現(xiàn)了劈裂. 由于非對(duì)易相空間中坐標(biāo)和動(dòng)量算符的形變導(dǎo)致了二維耦合諧振子的非對(duì)易能級(jí)出現(xiàn)非簡(jiǎn)并的情況. 這是很重要的性質(zhì), 為我們檢驗(yàn)空間的非對(duì)易性提供了可能的途徑. 2)非對(duì)易參數(shù)θ可以使n1?=0 的能級(jí)值增加, 而且隨著θ值的不斷增加, 能級(jí)會(huì)隨其線性變化. 但是對(duì)于n1=0的能級(jí),θ使其值先減少后增加. 參數(shù)?也有同樣的效果. 3)如果對(duì)非對(duì)易能譜取極限值, 即θ →0,? →0 , 結(jié)果會(huì)與通常對(duì)易空間中的二維諧振子的能譜一致. 4)受到耦合參數(shù)的影響, 能級(jí)會(huì)出現(xiàn)劈裂. 耦合項(xiàng)表示諧振子兩個(gè)維度之間的相互作用, 這種相互作用引起了能級(jí)的移動(dòng), 導(dǎo)致能級(jí)出現(xiàn)非簡(jiǎn)并的情況. 而且當(dāng)系統(tǒng)包含的耦合種類增多時(shí), 能級(jí)劈裂的程度也會(huì)增大. 同時(shí)發(fā)現(xiàn)坐標(biāo)耦合參數(shù)η和動(dòng)量耦合參數(shù)σ對(duì)能級(jí)的影響程度是一樣的, 但是坐標(biāo)動(dòng)量交叉耦合參數(shù)κ對(duì)能級(jí)的影響小于η和σ.