多個(gè)橢圓柱波浪力的一種解析解1)

趙 密 龍彭振 王丕光，2) 張 超 杜修力

* (北京工業(yè)大學(xué)城建學(xué)部建筑工程學(xué)院，北京 100124)

? (福州大學(xué)土木工程學(xué)院，福州 350116)

引言

近年來(lái)，中國(guó)的近海工程迅猛增加，如人工島，跨海橋梁等，對(duì)近海結(jié)構(gòu)的研究日益受到人們的重視.由于上述工程常年遭受波浪的威脅，其支撐結(jié)構(gòu)可能承受著強(qiáng)度相當(dāng)大的波浪力，而支撐結(jié)構(gòu)廣泛使用了多柱體，柱體截面形式不再局限于圓形，因此對(duì)非圓多柱體體系中波浪力的研究可為實(shí)際工程提供一定的理論指導(dǎo).

近海工程中對(duì)波浪力的研究根據(jù)結(jié)構(gòu)尺寸，可以劃分為對(duì)小尺度結(jié)構(gòu)所受波浪力的研究和對(duì)大尺度結(jié)構(gòu)所受波浪力的研究.其中小尺度結(jié)構(gòu)上的波浪力可以通過(guò)莫里森方程求解[1];當(dāng)結(jié)構(gòu)截面尺寸與波長(zhǎng)之比大于0.2 時(shí)，大尺寸結(jié)構(gòu)阻礙了波浪運(yùn)動(dòng)，波浪在結(jié)構(gòu)表面生成不可忽略的散射波，因此波浪力的計(jì)算需要考慮波浪散射現(xiàn)象[2-3].MacCamy和Fuchs[4]提出了繞射波浪理論來(lái)計(jì)算有限水域中大尺寸圓柱線性波浪力.當(dāng)波陡大時(shí)，波浪中的非線性成分增多，用線性波浪理論計(jì)算的結(jié)果誤差增大，國(guó)內(nèi)外學(xué)者就此提出了解決波浪二階作用的方法[5-6].Tao 等[7]和Song 等[8]利用比例邊界元法(SBFEM)分析短峰波在圓柱上繞射以及多個(gè)任意截面形狀柱體和線性波浪相互作用，比例邊界元對(duì)于解決波浪在柱面繞射問(wèn)題較高的求解效率.Wang 等[9]利用有限元方法，解決了傾斜圓柱的波浪繞射問(wèn)題.流場(chǎng)中只存在單個(gè)結(jié)構(gòu)的情形很少，大多數(shù)情況下近海結(jié)構(gòu)的承重構(gòu)件由多柱體構(gòu)成.Linton 和Evans[10]提出了計(jì)算多個(gè)圓柱附近波浪速度勢(shì)的簡(jiǎn)化公式.Kagemoto 和Yue[11]提出了一種精確代數(shù)方法來(lái)分析水波中多個(gè)三維物體之間的相互作用問(wèn)題.Chen 等[12]利用Null-Field 積分方程來(lái)解決波浪在多直立圓柱體中散射問(wèn)題，以免帶來(lái)用格林函數(shù)分析產(chǎn)生的不規(guī)則頻率問(wèn)題.繆國(guó)平等[13]假設(shè)柱體表面有若干波動(dòng)源，就100 根以上的單排圓樁體系在波浪中的響應(yīng)進(jìn)行了研究，得到了多柱體對(duì)流體干擾的特點(diǎn).Wang 等[14]將流場(chǎng)分為結(jié)構(gòu)附近的有限域和無(wú)限域，用橢圓吸收邊界模擬無(wú)限域，最后利用有限元方法求出波浪對(duì)群樁的影響，該方法可應(yīng)用到任意光滑截面的多柱體上.

實(shí)際工程中同樣存在非圓形截面柱體，如橢圓形和類(lèi)橢圓等.Chen 和Mei[15]基于橢圓柱坐標(biāo)系引入Mathieu 函數(shù)，將橢圓形固定平臺(tái)表面的波浪力分解為角向分量和徑向分量，分析了結(jié)構(gòu)表面繞射問(wèn)題，并得到相應(yīng)解.William[16]簡(jiǎn)化了文獻(xiàn)[15]中復(fù)雜級(jí)數(shù)展開(kāi)，并得到兩種近似方法，第一種適用于小曲率橢圓截面柱體，另一種利用格林函數(shù)獲得了柱體表面的流體速度勢(shì).Liu 等[17-18]利用線性繞射理論和傅里葉展開(kāi)，推導(dǎo)了任意光滑截面的鉛直柱體和截?cái)嘀w表面波浪力.Zhang 和Williams[19]研究了水平剛性橢圓形薄板對(duì)入射波浪的繞射效應(yīng).Bhatta[20]推導(dǎo)了橢圓截面樁和圓形截面樁的波浪力計(jì)算公式，并實(shí)現(xiàn)了前者到后者的變換.Wang 等[21-22]首先提出針對(duì)單根橢圓柱上地震引起的動(dòng)水力的解析解，再利用有限元方法改進(jìn)該發(fā)法為適用于工程的附加質(zhì)量矩陣方法，并且針對(duì)短峰波浪下的橢圓柱，推導(dǎo)得到波浪力的解析表達(dá)式，比較短峰波和一般線性波下橢圓柱周?chē)牟ㄅ?

對(duì)于多個(gè)非圓形截面柱體陣列結(jié)構(gòu)，Chatjigeorgiou等[23-25]利用Bessel 函數(shù)和Mathieu 函數(shù)的加法定理，依次研究了流體中橢圓截面群樁波浪散射問(wèn)題，橢圓柱和圓柱間的波浪散射問(wèn)題和截?cái)鄼E圓群樁上的波浪散射問(wèn)題.Lee[26]則應(yīng)用Collocation Multipole方法來(lái)解決橢圓截面多柱體間散射問(wèn)題，免除了Mathieu 函數(shù)加法定理的繁復(fù).Liu 等[27]利用傅里葉級(jí)數(shù)將徑向函數(shù)展開(kāi)，以求解任意光滑截面群樁(如余弦形截面、類(lèi)橢圓截面等)上的波浪力.

上述多個(gè)柱體波浪力解析分析方法中，多數(shù)考慮了入射波及入射波引起的單柱體散射波，但沒(méi)有考慮該散射波入射其他柱體后產(chǎn)生的第二次散射波以及高次散射波[25].本文基于橢圓坐標(biāo)系和繞射波理論等，推導(dǎo)得到考慮高次散射波的橢圓多柱體波浪力公式，研究波數(shù)等參數(shù)變化時(shí)高次波對(duì)總波浪力的貢獻(xiàn)，以期為實(shí)際工程中估算波浪力提供參考數(shù)據(jù).

1 問(wèn)題描述

1.1 控制方法和邊界條件

流場(chǎng)中橢圓形截面柱體的陣列如圖1 所示.假設(shè)所有柱體剛性，a為橢圓的半長(zhǎng)軸，b為橢圓的半短軸，底端固定在深度為h的流體中，流體無(wú)旋、無(wú)黏性并且不可壓縮.該多柱體體系受到與x軸成α，頻率為 ω，幅值為H/2 的簡(jiǎn)諧波浪作用.

圖1 柱體布置和坐標(biāo)系統(tǒng)Fig.1 Arrangement of bodies and coordinates systems

本文使用的橢圓柱坐標(biāo)系(ξ，μ，z)中，ξ和μ分別為橢圓柱坐標(biāo)系的徑向坐標(biāo)和角向坐標(biāo)，兩坐標(biāo)互相正交;坐標(biāo)原點(diǎn)位于橢圓柱底部，z軸沿柱體軸線向上.橢圓坐標(biāo)系和笛卡爾直角坐標(biāo)系轉(zhuǎn)換關(guān)系如下

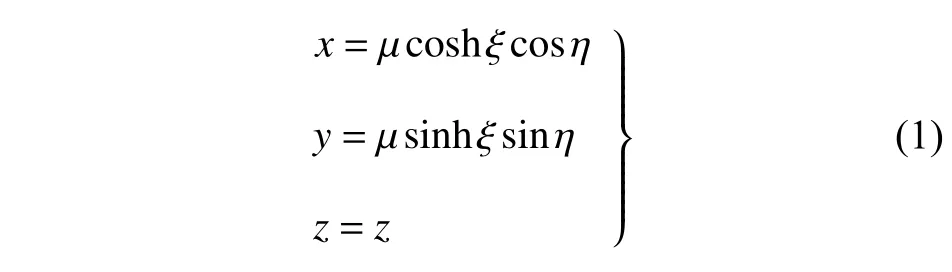
式中，μ2=a2-b2；ξ，μ和z取值范圍分別為0 ≤ξ＜∞，0≤μ＜2π和0≤z≤h.

簡(jiǎn)諧波浪下流場(chǎng)中波浪壓力為

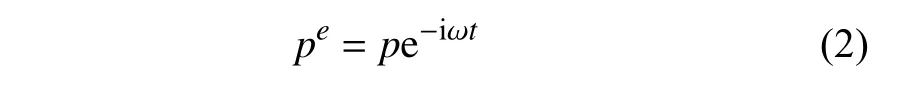
橢圓柱坐標(biāo)系中，頻域下的波浪壓力p滿(mǎn)足如下流體控制方程

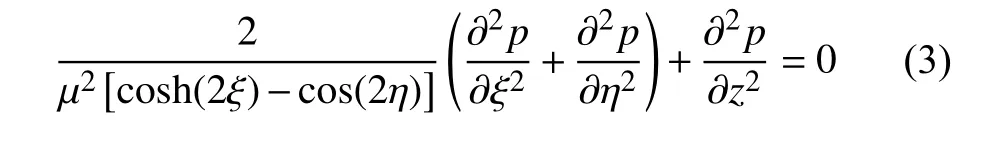
水體自由表面、剛性地面、水體與結(jié)構(gòu)交界面和無(wú)窮遠(yuǎn)處的邊界條件分別為

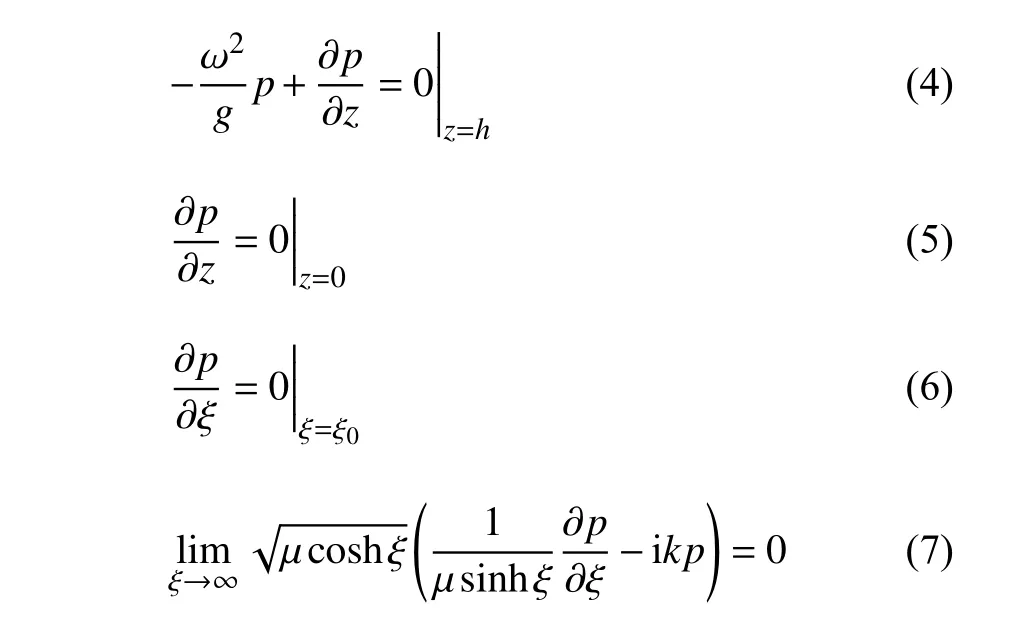
式中，波數(shù)k滿(mǎn)足 ω2=gktanh(kh) ; ξ0為柱體表面在柱體局部坐標(biāo)系中的徑向坐標(biāo).

1.2 波場(chǎng)分解

根據(jù)繞射波浪理論[4]:當(dāng)波浪入射后，波浪會(huì)在大尺寸結(jié)構(gòu)物表面產(chǎn)生散射波，入射波場(chǎng)和散射波場(chǎng)疊加后，形成的新的波場(chǎng).波浪入射后，多柱體陣列中柱體周?chē)牟▓?chǎng)不同于單柱體周?chē)牟▓?chǎng)，多柱體陣列中柱體上的波浪作用需要考慮入射波和散射波，其中散射波還需考慮其在柱間多次繞射，柱體上總的波浪力可以寫(xiě)為

式中，pSc不僅考慮了入射波浪在該柱體上引起的散射波，而且考慮了陣列中其他柱產(chǎn)生散射波、該散射波引起的高次散射波，因此pSc可以寫(xiě)為

對(duì)式(3)應(yīng)用分離變量法，p(ξ，η，z) 可以寫(xiě)為

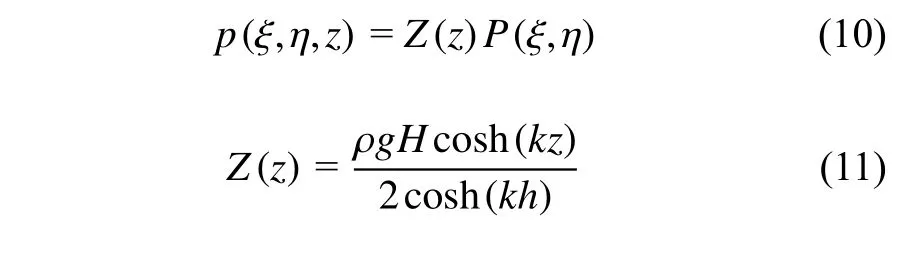
因此柱體總的波浪力可以寫(xiě)為

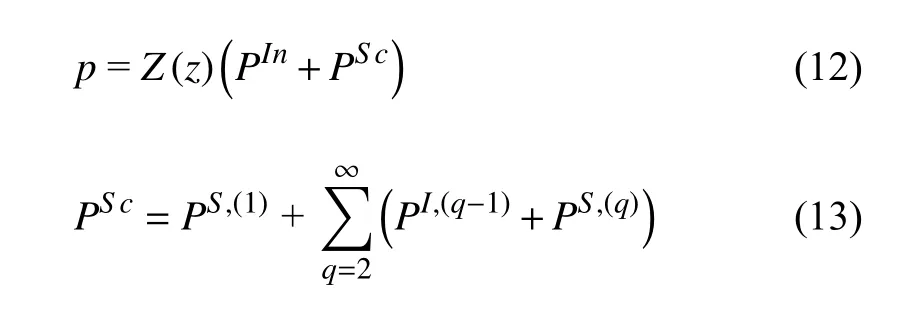
1.3 入射波浪壓力

如圖1 所示，流場(chǎng)中任意一點(diǎn)Q的入射波浪壓力可以表達(dá)為

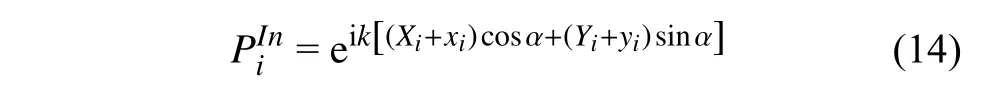
式中Xi和Yi是i號(hào)局部坐標(biāo)系原點(diǎn)在整體坐標(biāo)系中的坐標(biāo)，xi和yi是Q點(diǎn)在i號(hào)局部坐標(biāo)系中的坐標(biāo).

本文采用Abramowitz 和Stegun[28]提出的符號(hào)記法，因此在橢圓柱坐標(biāo)系下，入射波浪壓力可以表示為[25]

2 散射波浪壓力求解

2.1 散射波浪壓力

波浪入射到i號(hào)柱體后，產(chǎn)生的第一次散射波滿(mǎn)足式(3)～式 (5)和式(7)，其一般表達(dá)式可以寫(xiě)為

將式(15)和式(16)代入式(6)，求得

同一個(gè)流場(chǎng)中的其他柱產(chǎn)生的第一次散射波也會(huì)入射到i號(hào)柱體上，表示為.所有柱產(chǎn)生的散射波再入射到i柱后，波浪壓力可以寫(xiě)為

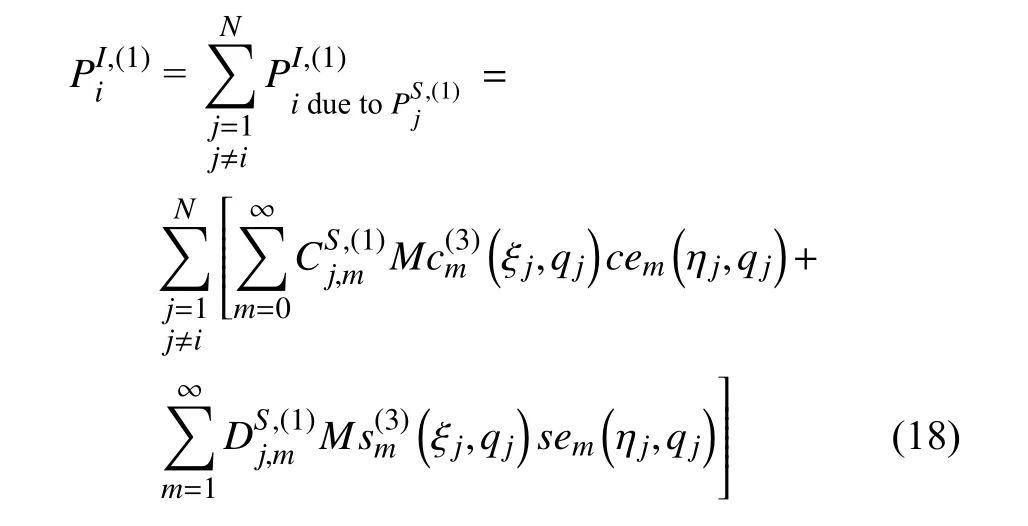
根據(jù)馬蒂厄函數(shù)的加法定理[29-30]，將式(18)中j號(hào)局部坐標(biāo)(ξj，μj)變換到i號(hào)局部坐標(biāo)系(ξi，μi)下，如下所示.馬蒂厄函數(shù)的加法定理詳見(jiàn)附錄1

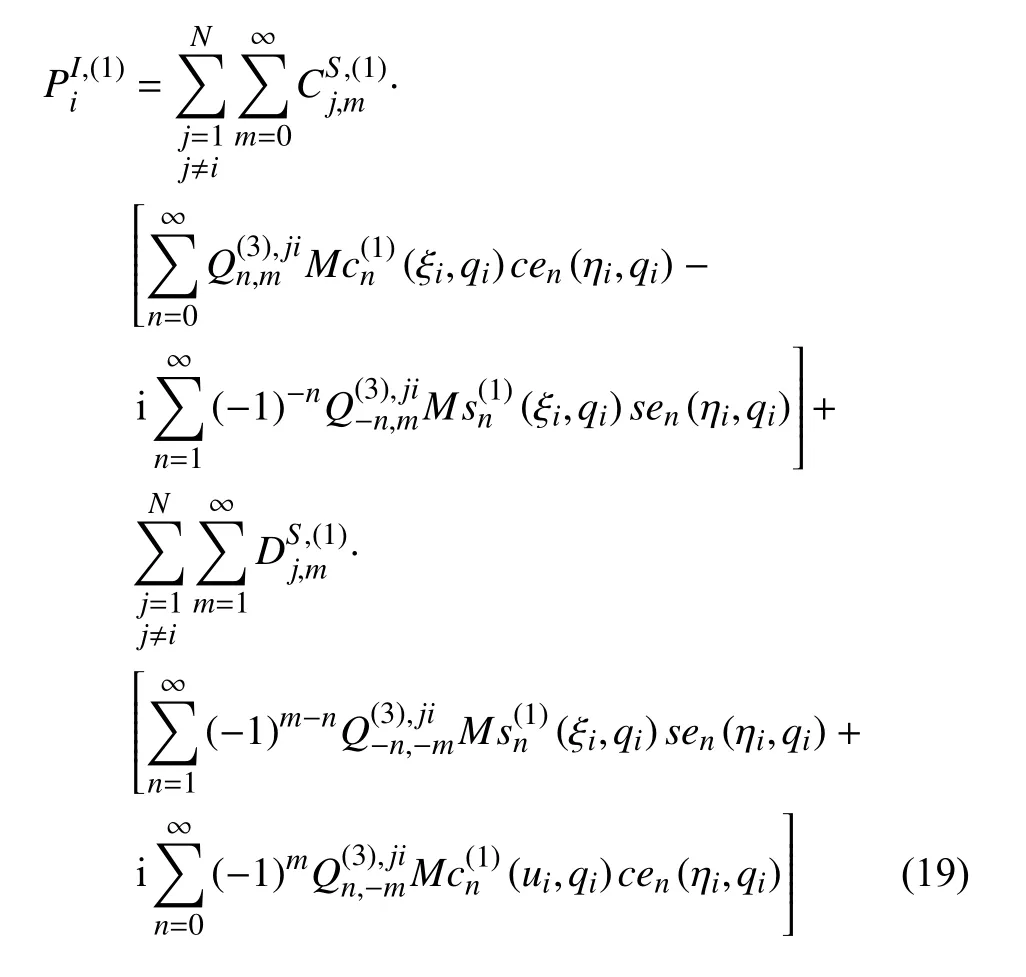
2.2 高次散射波浪壓力

多柱體陣列中低次散射波在柱間傳播，并在柱體表面產(chǎn)生高次散射波.其他柱產(chǎn)生的q-1 次散射波使i號(hào)柱體產(chǎn)生第q次散射波，i號(hào)柱體q次散射波浪力可以表示為

如式(18)，流場(chǎng)中其他柱產(chǎn)生的q-1 次散射波傳播到i號(hào)柱體上產(chǎn)生的波浪壓力可以寫(xiě)為

將式(21)轉(zhuǎn)換坐標(biāo)到i柱局部坐標(biāo)系下為

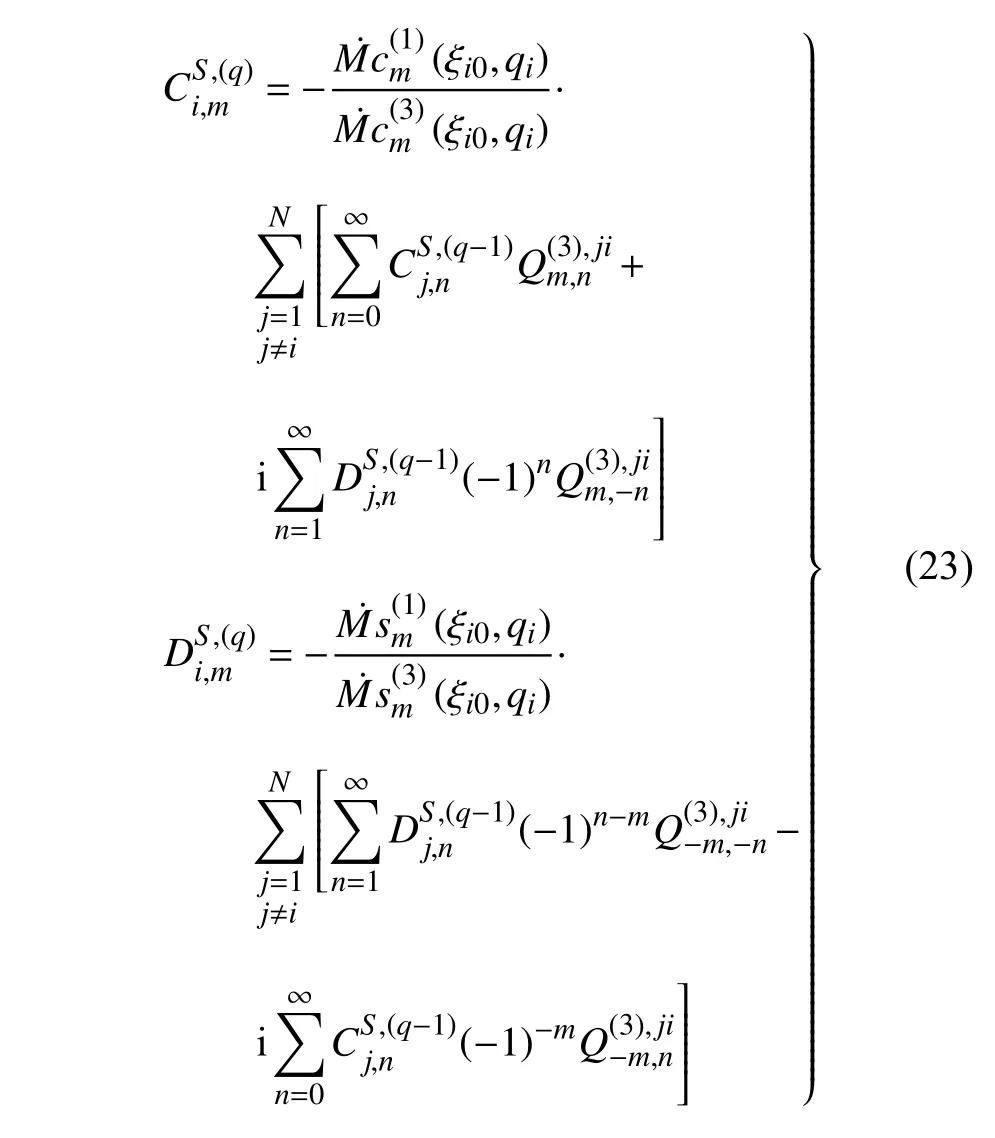
為求式(20)中的待定系數(shù)，將式(20)和式(22)代入式(6)，得到待定系數(shù)如下

2.3 總波浪力

多柱體體系中，i號(hào)柱體上總的波浪壓力可以寫(xiě)為

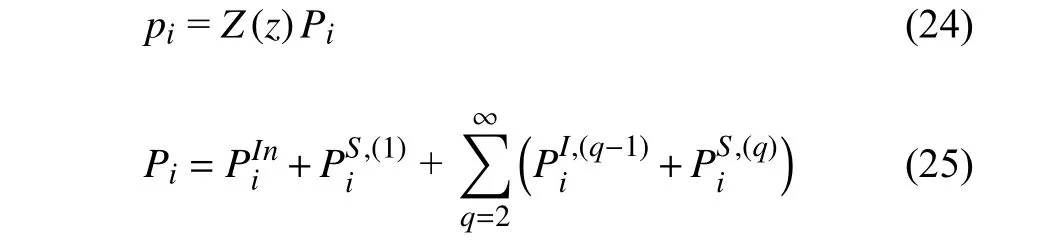
i號(hào)柱體所受的總波浪力可以表示為

3 數(shù)值算例

3.1 方法驗(yàn)證

首先，由于本方法在計(jì)算求解時(shí)會(huì)對(duì)式(25)中高次散射波的累加進(jìn)行截?cái)啵財(cái)鄷?huì)引入一定的截?cái)嗾`差，所以先討論該截?cái)嗾`差對(duì)計(jì)算結(jié)果的影響;其次，通過(guò)Wang 等[14]提出的波浪壓力數(shù)值解驗(yàn)證本文提出的橢圓形截面柱體波浪壓力的解析解.四柱體陣列如圖2 所示，圖2 中D為柱體間凈距，定義其與橢圓長(zhǎng)軸的比值Dr=1.0，4 個(gè)橢圓柱柱體具有相同的尺寸，長(zhǎng)軸和短軸比值a/b=1.5.圖3 給出了圖2 布置下不同截?cái)鄶?shù)q時(shí)，隨波數(shù)ka變化的曲線，可以看出當(dāng)q＞ 12 時(shí)本方法獲得波浪力計(jì)算結(jié)果基本穩(wěn)定，因此為使解析解求解高效且準(zhǔn)確，后續(xù)計(jì)算采用q=15 為高次散射波的截?cái)鄶?shù).圖4 為ka=1時(shí)，本文解析方法和數(shù)值方法得到的柱體上波浪壓力，圖5 為Dr=1 時(shí)，本文解析方法和數(shù)值方法得到的柱體上波浪力，假設(shè)波浪以?xún)蓚€(gè)入射角α入射;圖6 為ka=1 時(shí)，本文解析方法和數(shù)值方法得到的流場(chǎng)波浪壓力云圖，圖7 為解析方法與數(shù)值方法計(jì)算得到的C1 和C2 柱上波浪壓力的相對(duì)誤差;可以看出本文解和橢圓數(shù)值解相對(duì)誤差較小，各圖中本文解結(jié)果和數(shù)值解結(jié)果吻合良好.

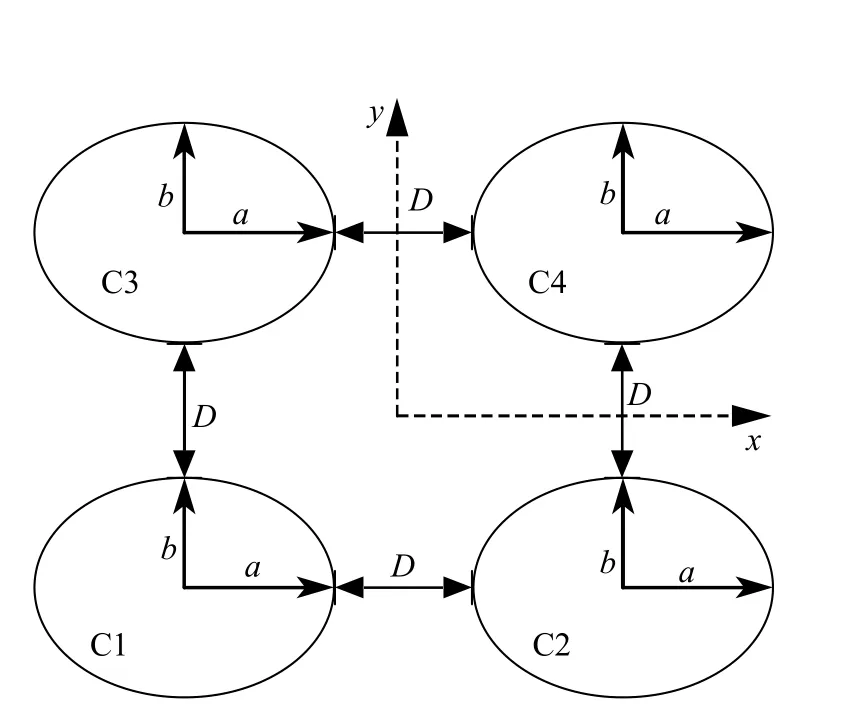
圖2 四柱體陣列圖Fig.2 Sketch of four bodies arranged in a square form.

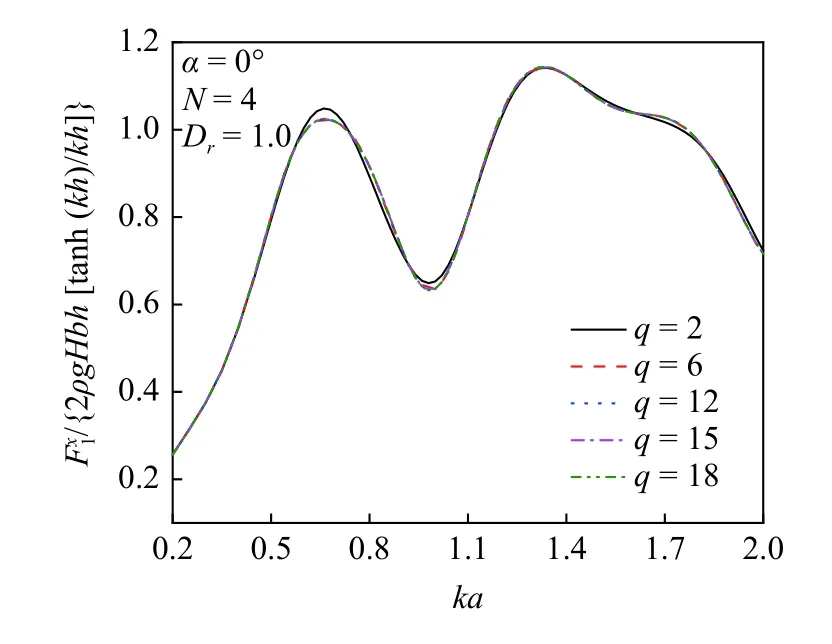
圖3 截?cái)嗾`差對(duì)本文解計(jì)算結(jié)果的影響Fig.3 Impacts of truncation error on the present method

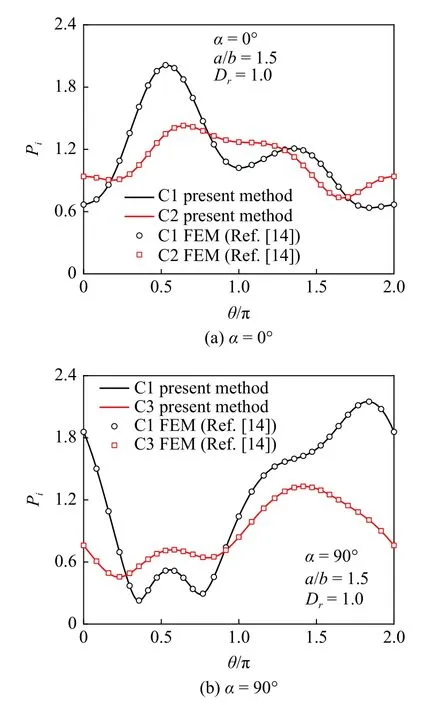
圖4 不同入射角(α=0° 和 α=90°)下數(shù)值解[14]與本文解的對(duì)比Fig.4 The wave pressures on bodies Piversus θ with N=4 and ka=1 obtained present method by and the FEM[14]

圖5 不同入射角(α=0° 和 α=90°)下數(shù)值解[14]與本文解的對(duì)比Fig.5 The wave forces on bodies Fi versus ka with N=4 obtained by the present method and FEM[14]

圖6 入射角 α=0° 時(shí)數(shù)值解[14]與本文解云圖Fig.6 The wave fields with N=4，α=0° and ka=1 obtained by the FEM[14] and present method

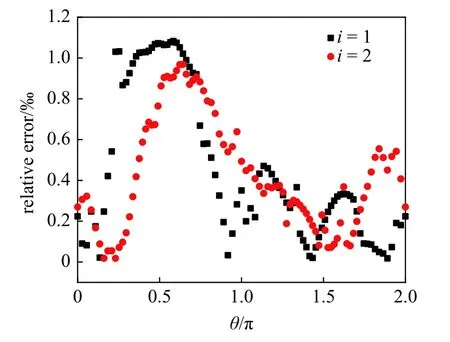
圖7 入射角 α=0° 時(shí)數(shù)值解與本文解的相對(duì)誤差Fig.7 The relative error of the wave pressure between the present method and the FEM with N=4，α=0° and ka=1

3.2 方法應(yīng)用

本節(jié)將討論高次波的影響，根據(jù)柱體排列設(shè)置了兩種柱體陣列:①雙柱(圖8)、②四柱(圖2).所示各工況中柱體截面尺寸相同，長(zhǎng)軸和短軸之比a/b=1.5.q=2 代表的曲線是不考慮高次散射波的解析解，q=15 代表的曲線是考慮高次散射波的解析解.從圖9 可以觀察到，單柱情況下的波浪力和多柱情況下的波浪力是不同的，該現(xiàn)象隨著柱數(shù)的增加而顯著，且和橢圓長(zhǎng)軸與水流方向的夾角有關(guān).

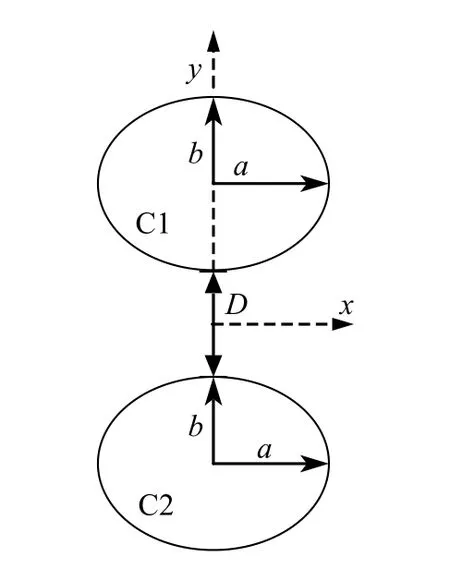
圖8 雙柱體陣列圖Fig.8 Sketch of arrangement of twin bodies standing side by side

圖10 給出了雙柱陣列中，高次散射波對(duì)柱體上波浪作用影響的結(jié)果.圖中縱坐標(biāo)為波浪力比值表示各柱體上考慮高次散射波的總波浪力，表示各柱體上不考慮高次散射波的總波浪力.圖中給出了3 種波浪入射角度下(0°，45°和90°)，ka取值在0.2～2.0 之間的結(jié)果.圖9(a)中，因?yàn)殛嚵醒豿軸對(duì)稱(chēng)所以C1 和C2 上的波浪力比值相等，高次波的影響不明顯;從圖10 (a)和圖10(b)中可以看出，當(dāng)ka小于0.5 時(shí)，高次波對(duì)兩柱體的影響可以忽略，當(dāng)ka大于0.5 后，高次波的影響增大到不可忽略.圖11 給出了ka=1 時(shí)Dr取值在0.5～5.0 之間的結(jié)果.圖11(b) 和圖11(c) 表明Dr大于2 后，二柱陣列的柱體受高次波的影響才會(huì)趨于減少，但即使凈距為柱體長(zhǎng)軸兩倍以上，高次波的影響仍然明顯;圖11(c)中，C1 受到上游柱體C2 的保護(hù)，C1 受到高次波的影響比C2 小.

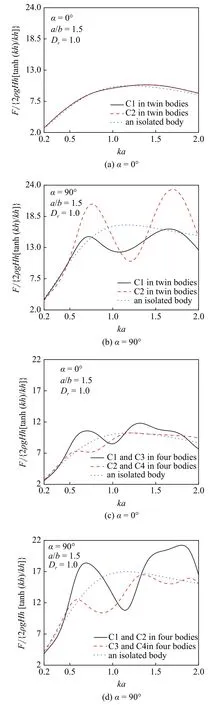
圖9 不同入射角(α=0° 和 α=90°)下兩種陣列的本文解與單柱解的對(duì)比Fig.9 The wave forces on bodies Fi versus ka with N=2 and 4 compared with that of an isolated body

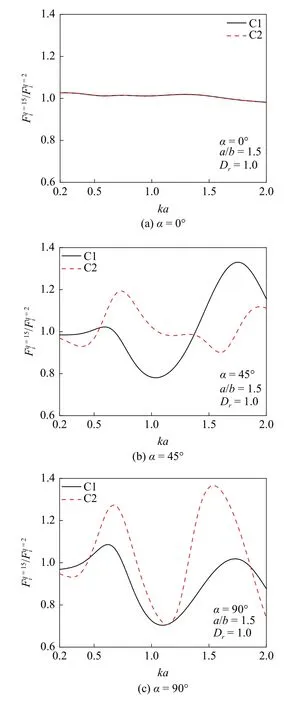
圖10 雙柱陣列中各柱體總受力比值Fig.10 Scaling values of total wave force on bodies versus ka as twin bodies standing side by side

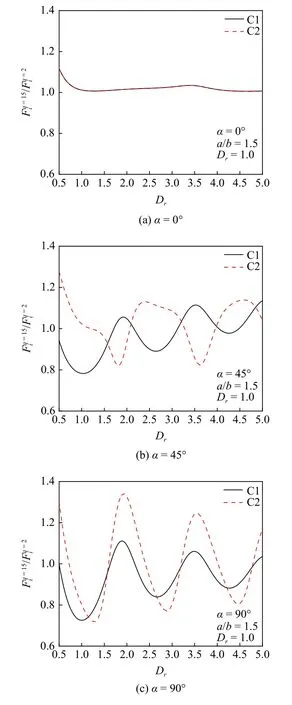
圖11 雙柱陣列中各柱體總受力比值Fig.11 Scaling values of total wave force on bodies versus Dr as twin bodies standing side by side

圖12 給出了四柱陣列中，高次散射波對(duì)柱體上波浪作用影響的結(jié)果.由于對(duì)稱(chēng)性，波浪沿x軸入射時(shí)(α=0°)，C1 和C3 計(jì)算結(jié)果相同，C2 和C4 計(jì)算結(jié)果相同;同理，波浪沿y軸入射時(shí)(α=90°)，C1 和C2 計(jì)算結(jié)果相同，C3 和C4 計(jì)算結(jié)果相同.比較兩個(gè)入射波浪方向不同的結(jié)果，可以發(fā)現(xiàn)因?yàn)橹w在x軸上的投影面積大于柱體在y軸上的投影面積，所以波浪沿y軸入射時(shí)高次波對(duì)柱體所受波浪力的影響更大.圖13 給出了ka=1 時(shí)Dr取值在0.5～5.0 之間的結(jié)果.四柱陣列的下游柱體波浪力比值在0.5 ＜Dr＜ 1.0 間大于上游柱體的比值，在Dr＞ 2.0 之后才小于上游柱體的比值并趨于減小.

圖12 四柱陣列中各柱體總受力比值Fig.12 Scaling values of total wave force on bodies versus ka as four bodies arranged in a square form

圖13 四柱陣列中各柱體總受力比值Fig.13 Scaling values of total wave force on bodies versus Dr as four bodies arranged in a square form

圖14 和圖15 給出了柱體數(shù)量不同的情況下，C1 上波浪力比值隨參數(shù)(ka，Dr)的變化.綜合來(lái)看，隨ka和Dr增加，四柱陣列中C1 波浪力比值變化，比雙柱陣列情況下的比值變化要?jiǎng)×?隨著柱體數(shù)量的增多，由于疊加效應(yīng)，高次波影響也隨之增加.

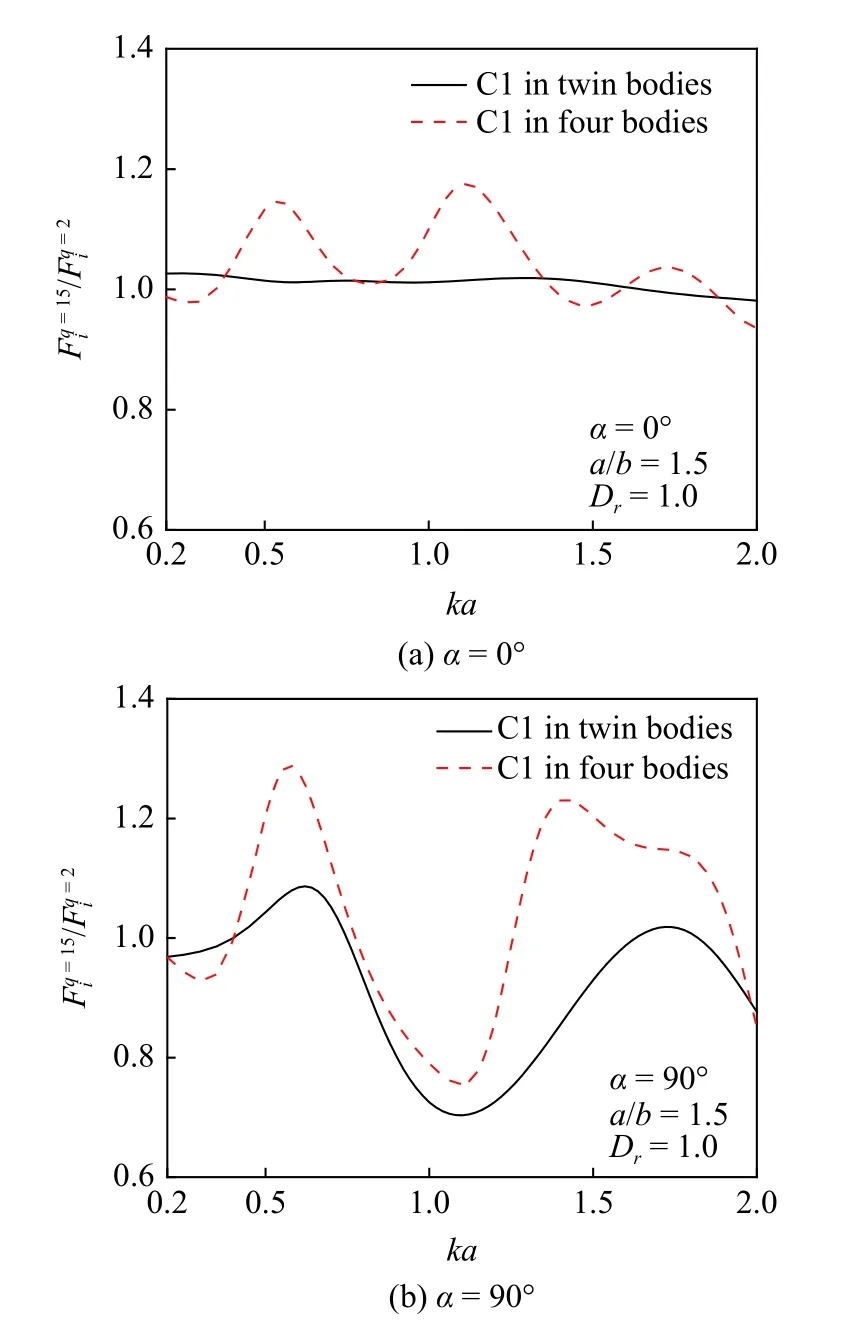
圖14 兩種陣列中C1 柱體總受力比值Fig.14 Scaling values of C1 versus ka in two arrangements

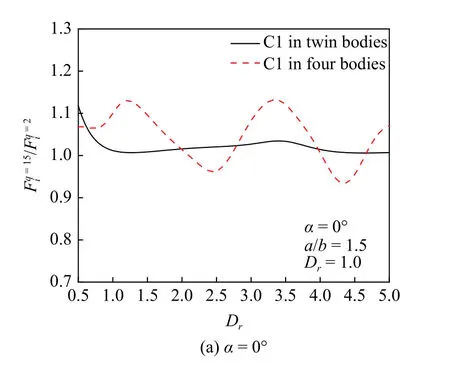
圖15 兩種陣列中C1 柱體總受力比值Fig.15 Scaling values of C1 versus Dr in two arrangements

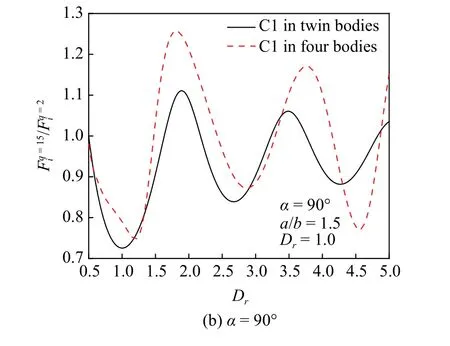
圖15 兩種陣列中C1 柱體總受力比值(續(xù))Fig.15 Scaling values of C1 versus Dr in two arrangements (continued)

表1 對(duì)比了本文解和參考解[14]在ka=1 時(shí)，不同柱數(shù)，不同柱間距時(shí)波浪力計(jì)算效率.因?yàn)橛邢拊椒ㄓ?jì)算耗時(shí)和網(wǎng)格單元?jiǎng)澐执笮∫约熬W(wǎng)格數(shù)目成正相關(guān)，所以當(dāng)柱數(shù)增加或者柱間距增加后，用來(lái)模擬水域的單元也隨之增多，所以本文解比參考解效率高.

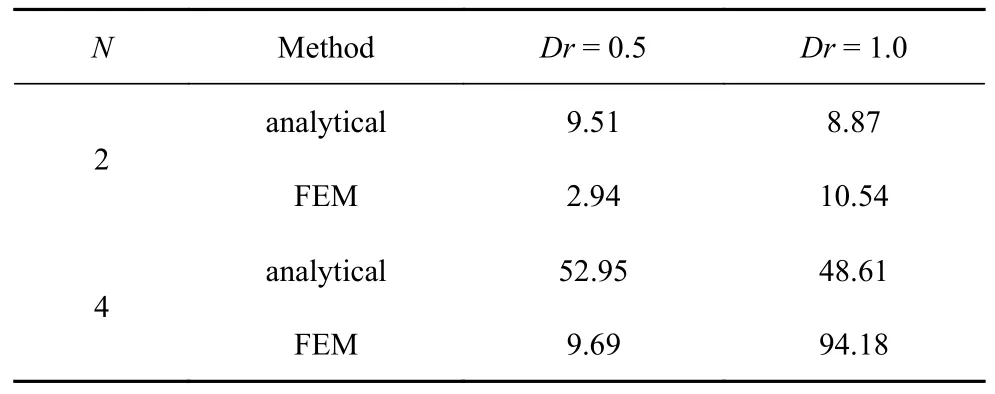
表1 計(jì)算波浪力的用時(shí) (s)Table 1 The numerical costs for calculating the total wave forces (s)

4 結(jié)論

根據(jù)繞射波理論等，基于橢圓柱坐標(biāo)系，首先通過(guò)求解馬蒂厄方程，得到橢圓單柱體結(jié)構(gòu)波浪壓力公式，再考慮多柱體體系中高次散射波問(wèn)題，推導(dǎo)得到多柱體體系中橢圓柱體結(jié)構(gòu)波浪力計(jì)算公式.本文方法與已有數(shù)值方法對(duì)比結(jié)果表明，本文解和數(shù)值解吻合的較好，而當(dāng)柱數(shù)目增加或柱間距增大時(shí)，本文解的計(jì)算效率比有限元方法的高.

將本文方法應(yīng)用于計(jì)算雙柱陣列和四柱陣列的波浪力，分析了高次散射波對(duì)結(jié)構(gòu)所受波浪作用的影響.結(jié)果表明:波數(shù)ka＜0.5 時(shí)，高次散射波影響較小，大波數(shù)的情況下，不能忽略高次波的影響;隨著柱體間距離的增加，高次波的影響有減小的趨勢(shì)，但仍存在波動(dòng);高次波對(duì)上游柱體波浪力的影響比下游柱體大;多柱體體系中，柱體數(shù)量增加后，柱體產(chǎn)生的高次散射波會(huì)疊加，高次波影響也隨之增加，而結(jié)構(gòu)所受的高次波作用因參數(shù)發(fā)生的波動(dòng)會(huì)變劇烈.

附錄1

Chatjigeorgiou 等[17]在S?rmar k 等[21]的基礎(chǔ)上化簡(jiǎn)了將馬蒂厄函數(shù)的加法定理，具體可以表示為

式中，Jm(·) 為第一 類(lèi)m階貝塞爾函數(shù)，Ym(·) 為第二類(lèi)m階貝塞爾函數(shù)，為第一 類(lèi)m階漢克爾函數(shù)，為第二類(lèi)m階漢克爾函數(shù).當(dāng)n-p和s-m為奇數(shù)時(shí)，d′和d為0.