液體火箭發(fā)動(dòng)機(jī)試驗(yàn)流量測量系統(tǒng)可靠性評定

楊懿,郭亞男,王永鵬,賈志杰,陳文麗,呂守國,吉喆

(北京航天試驗(yàn)技術(shù)研究所,北京100074)

0 引言

液體火箭發(fā)動(dòng)機(jī)試驗(yàn)中,液體推進(jìn)劑的流量數(shù)據(jù)是計(jì)算發(fā)動(dòng)機(jī)比沖量的重要數(shù)據(jù),測量數(shù)據(jù)的準(zhǔn)確性和可靠性關(guān)系到對火箭的運(yùn)載能力和射程的評估[1]。流量測量系統(tǒng)的高可靠性是保障系統(tǒng)長期正常、穩(wěn)定工作,測量數(shù)據(jù)滿足試驗(yàn)任務(wù)書要求的重要基礎(chǔ)。

在可靠性研究和實(shí)踐領(lǐng)域,一般從結(jié)構(gòu)可靠性和性能可靠性兩個(gè)維度對產(chǎn)品/系統(tǒng)的可靠性進(jìn)行評估。性能可靠性一般是指產(chǎn)品/系統(tǒng)在規(guī)定工作條件下、規(guī)定工作時(shí)間內(nèi),其性能參數(shù)滿足規(guī)定的容許限要求的概率[2-3]。如導(dǎo)彈的射程、著彈點(diǎn)的準(zhǔn)確度,測量系統(tǒng)的數(shù)據(jù)準(zhǔn)確度等等。結(jié)構(gòu)可靠性一般是指產(chǎn)品/系統(tǒng)保持正常工作、性能滿足規(guī)定要求的能力[4]。在發(fā)動(dòng)機(jī)試驗(yàn)中,測量系統(tǒng)的性能可靠性與結(jié)構(gòu)可靠性是同等重要的。性能可靠性是測量系統(tǒng)能夠投入使用的前提和保障測量數(shù)據(jù)質(zhì)量的重要基礎(chǔ)。結(jié)構(gòu)可靠性是保障測量系統(tǒng)能夠長久、正常運(yùn)行的重要基礎(chǔ)。在測量系統(tǒng)的工作壽命周期內(nèi),不僅需要具備優(yōu)越的性能可靠性,還需要具備保持其性能可靠性的能力。多位研究人員對產(chǎn)品的性能可靠性、功能可靠性評估方法進(jìn)行了研究。

陳保家等人[5]從軸承運(yùn)行數(shù)據(jù)中提取狀態(tài)信息和設(shè)備的閾值信息,采用基于比例協(xié)變量和Logistic回歸模型相結(jié)合的可靠性評估方法求解故障率和協(xié)變量函數(shù),并不斷更新故障率函數(shù)信息,從而提高航空發(fā)動(dòng)機(jī)軸承運(yùn)行可靠性評估精度和可信性。但是由于航天產(chǎn)品試驗(yàn)的測量系統(tǒng)一般由多個(gè)組成單元或者設(shè)備構(gòu)成,彼此之間的測量原理、測量參數(shù)類型存在差異,確認(rèn)測量系統(tǒng)的閾值信息存在較大的困難,該方法不適用于對測量系統(tǒng)可靠性的評估。

張曌等人[6]采用故障樹方法分析多個(gè)影響測量系統(tǒng)可靠性的因素,給出了影響因素的重要度排序,并對測量系統(tǒng)進(jìn)行故障診斷,有效提高了系統(tǒng)的平均無故障時(shí)間和連續(xù)工作時(shí)間。但是該方法重點(diǎn)在于實(shí)現(xiàn)測量系統(tǒng)的定性分析,缺少對測量系統(tǒng)性能可靠性的分析,也未給出系統(tǒng)可靠性的定量評價(jià)方法。

葉亮等人[7]根據(jù)軸承的數(shù)據(jù)特征,采用不同的指標(biāo)描述軸承振動(dòng)性能,建立不同指標(biāo)和振動(dòng)性能可靠性之間的關(guān)系。采用基于信息理論和概率統(tǒng)計(jì)的方法計(jì)算、分析軸承振動(dòng)性能的可靠度。其研究的重點(diǎn)是基于數(shù)據(jù)特征來描述性能可靠性,對本文有一定啟發(fā)。該方法并未考慮結(jié)構(gòu)功能可靠性對產(chǎn)品可靠性的影響,而且當(dāng)發(fā)動(dòng)機(jī)在多工況下試驗(yàn)時(shí),流量的變化必然導(dǎo)致數(shù)據(jù)表征指標(biāo)相應(yīng)變化,增加了評估的難度,并不適用本文的研究方向。

張根保等人[8]將機(jī)電產(chǎn)品分解成最小的元?jiǎng)幼鲉卧?將產(chǎn)品性能可靠性問題轉(zhuǎn)化為元?jiǎng)幼鲉卧阅芸煽啃詥栴}。根據(jù)元?jiǎng)幼鲉卧獌?nèi)部零件和結(jié)構(gòu)的依賴耦合關(guān)系,建立隨機(jī)過程和元?jiǎng)幼鲉卧阅芸煽啃苑治瞿Ｐ?分析產(chǎn)品性能退化與特定功能之間的關(guān)系。該方法適用于對機(jī)械產(chǎn)品的結(jié)構(gòu)可靠性評估,缺少對性能數(shù)據(jù)的分析。而測量系統(tǒng)性能可靠性指標(biāo)主要以大量實(shí)測數(shù)據(jù)為基礎(chǔ),對實(shí)測數(shù)據(jù)的合理分析是判斷性能可靠性的主要依據(jù)。

綜上所述,單從結(jié)構(gòu)可靠性或者性能可靠性對液體火箭發(fā)動(dòng)機(jī)試驗(yàn)流量測量系統(tǒng)的可靠性進(jìn)行分析是遠(yuǎn)遠(yuǎn)不夠的。需要將性能可靠性和結(jié)構(gòu)可靠性結(jié)合起來,實(shí)現(xiàn)航天產(chǎn)品試驗(yàn)測量系統(tǒng)可靠性的定量分析。本文給出了行業(yè)背景下測量系統(tǒng)性能可靠性和結(jié)構(gòu)可靠性的定義,將試驗(yàn)數(shù)據(jù)作為性能可靠性的衡量指標(biāo),將測量系統(tǒng)組成單元的失效數(shù)作為結(jié)構(gòu)可靠性的衡量指標(biāo)。從性能可靠性和結(jié)構(gòu)可靠性兩個(gè)維度對液體火箭發(fā)動(dòng)機(jī)流量測量系統(tǒng)的可靠性進(jìn)行評估。對行業(yè)內(nèi)技術(shù)人員評估測量系統(tǒng)指標(biāo)具有重要的參考價(jià)值。

1 流量測量系統(tǒng)

在液體火箭發(fā)動(dòng)機(jī)試驗(yàn)中,流量測量系統(tǒng)一般由渦輪流量計(jì)、信號(hào)發(fā)生器、二次儀表和數(shù)據(jù)采集系統(tǒng)組成[9]。系統(tǒng)原理組成如圖1所示。

圖1 流量測量系統(tǒng)圖Fig.1 Diagram of flow measurement system

流量參數(shù)的基本測量原理:推進(jìn)劑經(jīng)過貯箱增壓后,推動(dòng)渦輪流量計(jì)的葉輪轉(zhuǎn)動(dòng)。轉(zhuǎn)動(dòng)葉輪切割信號(hào)發(fā)生器所產(chǎn)生的磁力線,生成正弦波式感生電動(dòng)勢。當(dāng)管路橫截面積不變時(shí),感生電動(dòng)勢的頻率與推進(jìn)劑流速成正比。頻率和被測流量的線性關(guān)系為

式中:Q為通過傳感器的體積流量,L/s;A,B為傳感器常數(shù);f為傳感器輸出頻率,Hz。

2 流量測量系統(tǒng)可靠性定義及評定方法

2.1 測量系統(tǒng)性能可靠性定義

根據(jù)引言中性能可靠性的定義,針對測量系統(tǒng)的特殊性,需要對其性能可靠性的定義進(jìn)行相應(yīng)的擴(kuò)充,其定義如下。

測量系統(tǒng)性能可靠性是指在規(guī)定的時(shí)間內(nèi)和規(guī)定的條件下,測量系統(tǒng)工作正常,系統(tǒng)輸出的測量數(shù)據(jù)滿足所規(guī)定的允許限度要求的能力或概率。其中,規(guī)定時(shí)間是指系統(tǒng)完成試驗(yàn)測量任務(wù)所需的時(shí)間。規(guī)定條件是指系統(tǒng)工作時(shí)所處的符合對應(yīng)要求的全部外界條件,如環(huán)境、溫濕度、振動(dòng)等。正常工作是指系統(tǒng)的各項(xiàng)組成單元均工作正常。

2.2 性能可靠性評定方法

大量的試驗(yàn)統(tǒng)計(jì)數(shù)據(jù)表明,液體火箭發(fā)動(dòng)機(jī)性能參數(shù)(推力、比沖、流量、混合比等)一般服從正態(tài)分布[2]。因此,設(shè)系統(tǒng)的性能X~N(μ,σ2),其中,μ,σ未知。對X取容量為n的樣本x1,x2,…,xn,通常要求系統(tǒng)的性能參數(shù)保持在容許的偏差范圍之內(nèi),則

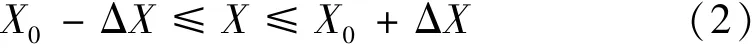
式中:X0為性能參數(shù)的額定值;ΔX為性能參數(shù)容許的偏差范圍。

可以得到

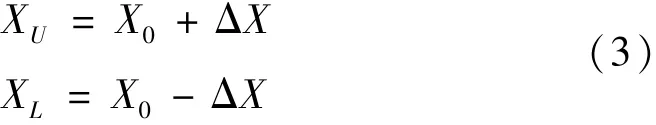
式中:XU為性能參數(shù)的容許上限;XL為性能參數(shù)的容許下限。

在可靠性理論中,根據(jù)產(chǎn)品/系統(tǒng)的功能定位,對性能參數(shù)的要求大致可以分為3類[10]:

1)單側(cè)下限參數(shù)性能可靠性

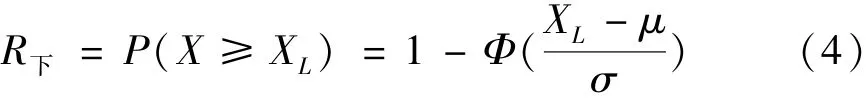
2)單側(cè)上限參數(shù)性能可靠性

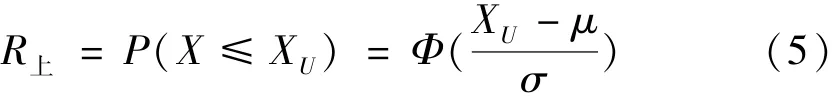
3)雙側(cè)參數(shù)性能可靠性,即XL≤X≤XU。

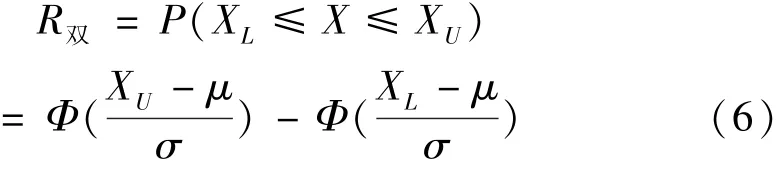
一般情況下,只能通過產(chǎn)品的有限次試驗(yàn)或者有限個(gè)系統(tǒng)試驗(yàn)測試數(shù)據(jù)得到性能X的樣本均值與樣本標(biāo)準(zhǔn)差S。以樣本均值與樣本標(biāo)準(zhǔn)差S分別替代μ,σ求得性能可靠性的點(diǎn)估計(jì)。區(qū)間估計(jì)的推導(dǎo)方法為[2]等價(jià)于令,

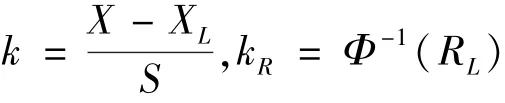
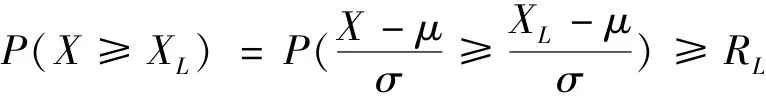
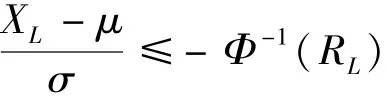
則有,

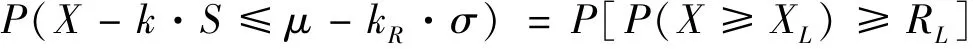
通過調(diào)整變換得到

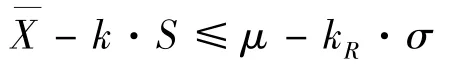
等價(jià)于

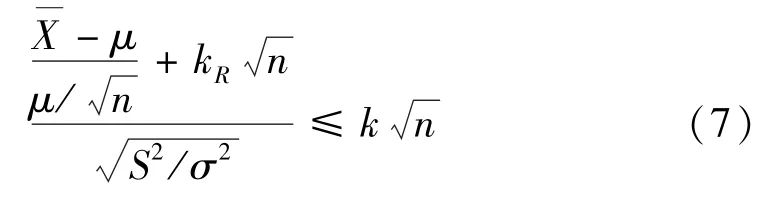
在置信水平γ下,計(jì)算γ,即

由上述分析可知,當(dāng)給定置信度γ,已知參數(shù)k,n時(shí),即可求出kR,從而求得性能可靠性單側(cè)下限RL=Φ(kR)。由于求解計(jì)算的過程較為較為復(fù)雜,可以通過查表的方式進(jìn)行求解。求解方法如下:

2)根據(jù)給定的置信水平γ,樣本量n和k值,對于單側(cè)置信下限可靠度,可以查參考文獻(xiàn)[11],求解kR值,從而可得到置信下限可靠度RL=Φ(kR)。對于雙側(cè)置信下限估計(jì),可以查參考文獻(xiàn)[12]求得近似解。

2.3 測量系統(tǒng)結(jié)構(gòu)可靠性定義

根據(jù)引言中結(jié)構(gòu)可靠性的定義,針對測量系統(tǒng)的特殊性,其結(jié)構(gòu)可靠性的擴(kuò)充定義為:

測量系統(tǒng)結(jié)構(gòu)可靠性是指測量系統(tǒng)各組成單元在規(guī)定的時(shí)間內(nèi)和規(guī)定的條件下正常工作的概率。其中,規(guī)定時(shí)間是指測量系統(tǒng)在系統(tǒng)調(diào)試、正式試驗(yàn)等程序中的工作時(shí)間。規(guī)定條件主要是指測量系統(tǒng)需要滿足試驗(yàn)任務(wù)書規(guī)定的相關(guān)要求。

2.4 結(jié)構(gòu)可靠性評定方法

在液體火箭發(fā)動(dòng)機(jī)試驗(yàn)以及系統(tǒng)調(diào)試等過程中,影響流量測量系統(tǒng)結(jié)構(gòu)可靠性的因素主要有以下幾個(gè)方面:

1)渦輪流量計(jì)的軸承、葉輪等部件長時(shí)間受氣流、低溫介質(zhì)的高速推動(dòng),容易損壞。

2)受液氧、液氫等低溫介質(zhì)的影響,渦輪流量計(jì)外接信號(hào)發(fā)生器頻繁處于溫差變化較大的環(huán)境中,嚴(yán)重影響信號(hào)發(fā)生器的工作穩(wěn)定性。接插件暴露在空氣中,冷凝現(xiàn)象也影響了接插件的可靠性。

基于上述原因,對流量測量系統(tǒng)的結(jié)構(gòu)可靠性進(jìn)行研究和分析,對提高流量測量系統(tǒng)可靠性具有重要的意義。氫氧火箭發(fā)動(dòng)機(jī)試驗(yàn)流量測量系統(tǒng)可靠性框圖如圖2所示。

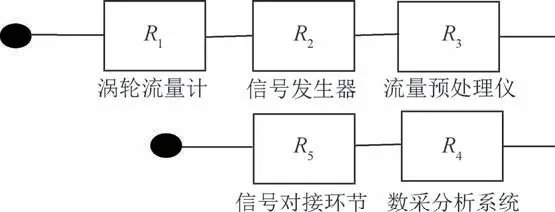
圖2 流量測量系統(tǒng)可靠性框圖Fig.2 Reliability block diagram of flow measurement system

圖2 中,信號(hào)對接環(huán)節(jié)主要是指流量測量系統(tǒng)在運(yùn)行過程中,設(shè)備接插件(如流量計(jì)信號(hào)發(fā)生器的插頭、流量預(yù)處理儀的插頭等)的對接狀態(tài)。根據(jù)以往的統(tǒng)計(jì)數(shù)據(jù)顯示,接插件的對接狀態(tài)也是影響流量測量系統(tǒng)是否正常工作的重要因素之一。因此,本文將信號(hào)對接環(huán)節(jié)作為影響系統(tǒng)可靠性的因素,納入可靠性框圖中。

從圖2可知,流量測量系統(tǒng)結(jié)構(gòu)可靠性為一般串聯(lián)系統(tǒng)。工程應(yīng)用中一般采用L-M法對系統(tǒng)可靠性進(jìn)行近似求解。根據(jù)串聯(lián)型系統(tǒng)可靠性的性質(zhì),系統(tǒng)的可靠性由組成系統(tǒng)的最薄弱單元決定[2]。

圖2 中,渦輪流量計(jì)、信號(hào)發(fā)生器、流量預(yù)處理儀(R1~R3)的單元失效類型為壽命型,數(shù)采分析系統(tǒng)(R4)和信號(hào)對接環(huán)節(jié)(R5)的失效類型為成敗型。為便于可靠性試驗(yàn)信息的折合,需要將不同失效類型數(shù)據(jù)轉(zhuǎn)換為相同失效類型數(shù)據(jù)。本文將指數(shù)壽命型試驗(yàn)信息轉(zhuǎn)換為二項(xiàng)成敗型試驗(yàn)信息。文獻(xiàn)[13-14]介紹了指數(shù)型與成敗型試驗(yàn)數(shù)據(jù)的折合轉(zhuǎn)換方法,本文不再贅述。

L-M法的基本原理[10]為:設(shè)系統(tǒng)由k個(gè)單元組成,試驗(yàn)數(shù)據(jù)為(ni,Fi),其中,i=1,2,…,k,ni為第i個(gè)單元的試驗(yàn)次數(shù),Fi為第i個(gè)單元的失敗試驗(yàn)次數(shù)。則系統(tǒng)可靠性最大似然估計(jì)為

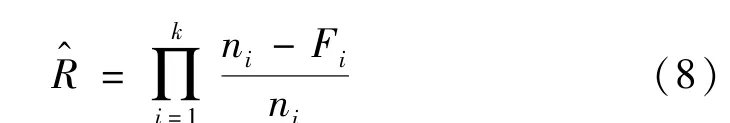
將系統(tǒng)各組成單元的試驗(yàn)次數(shù)按照從小到大的順序排列,{n(1),n(1),…,n(k)}為將ni,(i=1,2,…,k)重新進(jìn)行排列后的數(shù)據(jù)集,取系統(tǒng)等效試驗(yàn)次數(shù)為

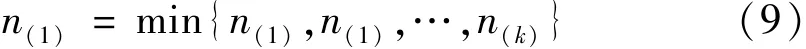
系統(tǒng)等效失敗次數(shù)為

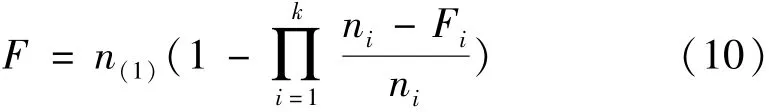
設(shè)[F]為不超過F的整數(shù)部分,在給定置信水平γ時(shí),通過公式(11),(12)計(jì)算R1和R2。再采用線性插值法,得到失敗次數(shù)為F時(shí)的系統(tǒng)可靠性置信下限RL。

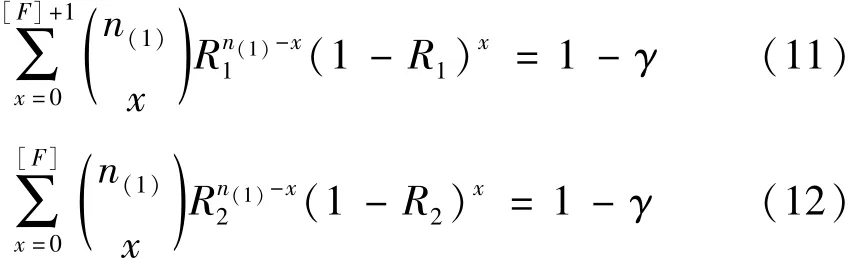
3 案例分析

以某型號(hào)發(fā)動(dòng)機(jī)試驗(yàn)為例,對流量測量系統(tǒng)可靠性進(jìn)行評定。

3.1 測量系統(tǒng)性能可靠性評定

根據(jù)任務(wù)書的要求,在某工況下,液氧額定流量為5.200 L/s,下限為5.096 L/s,上限為5.304 L/s,給定置信水平γ=0.9。選取該工況下10個(gè)子樣的液氧流量數(shù)據(jù),如表1所示。

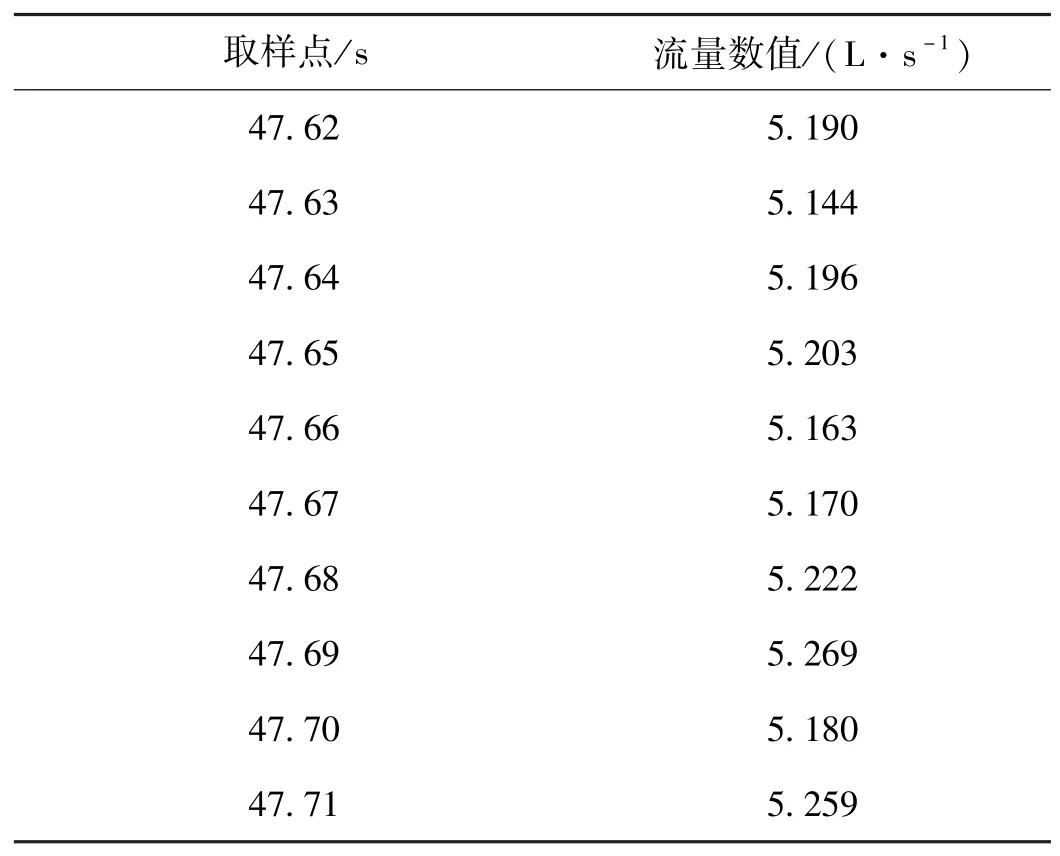
表1 液氧流量數(shù)據(jù)表Table.1 Data sheet of liquid oxygen flow

可靠度估值

根據(jù)n=10,γ=0.9,k1=2.5660,k2=2.5859,查《正態(tài)分布雙側(cè)容許限系數(shù)表》得到p1=0.00745,p2=0.00726。計(jì)算得到測量系統(tǒng)性能可靠性下限RL=1-(p1+p2)=0.98529。

3.2 測量系統(tǒng)結(jié)構(gòu)可靠性評定

取置信水平γ=0.9,測量系統(tǒng)各組成單元的等效試驗(yàn)數(shù)據(jù)如表2所示。

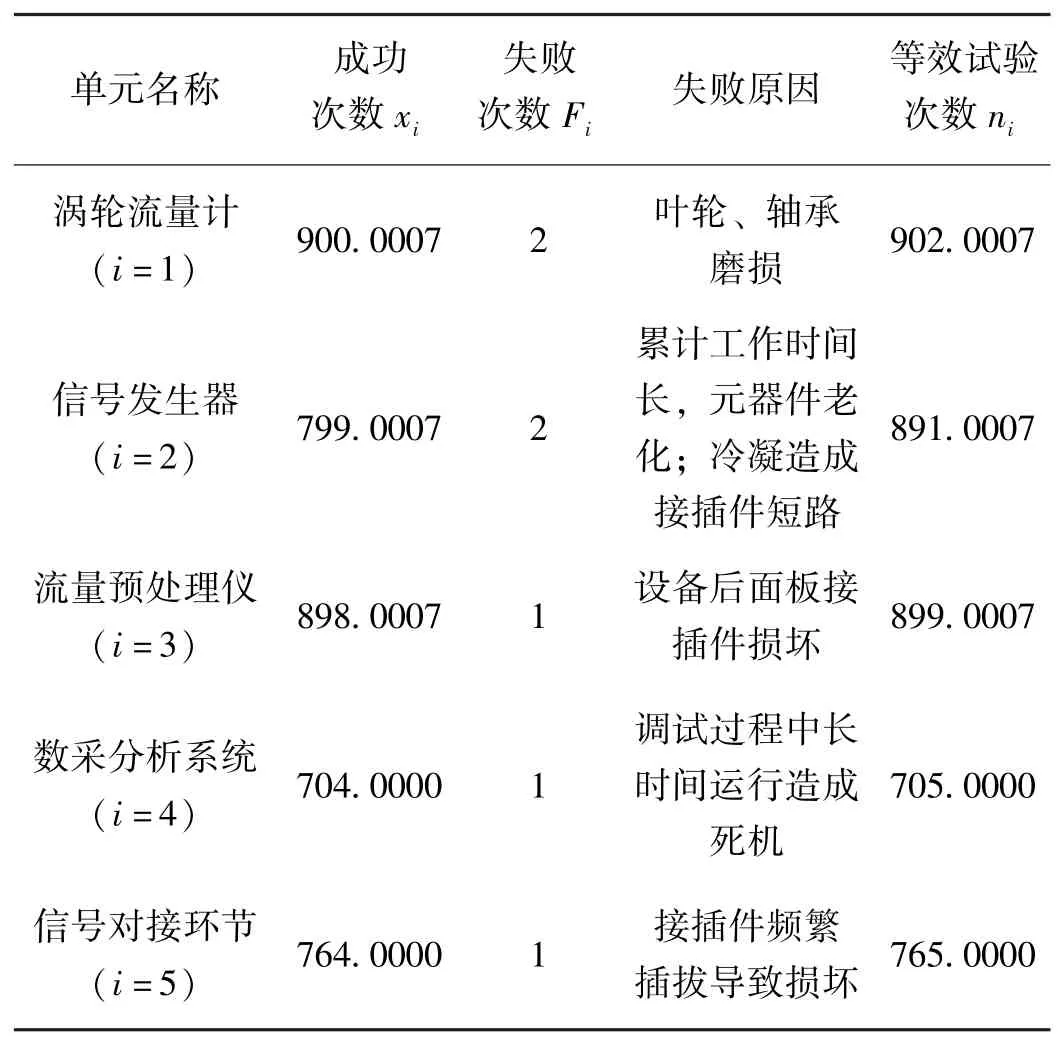
表2 流量測量系統(tǒng)各組成單元等效試驗(yàn)數(shù)據(jù)表Table.2 Equivalent test data of each unit of flow measurement system

根據(jù)表2的數(shù)據(jù),將系統(tǒng)各組成單元的試驗(yàn)數(shù)按照從小到大的順序排列{705.0000,765.0000,891.0007,899.0007,902.0007},取系統(tǒng)等效試驗(yàn)次數(shù)為n(1)=705.0000。則最大似然估計(jì)為

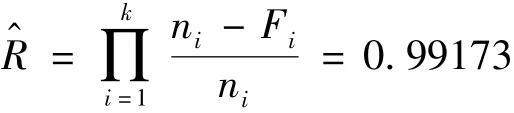
等效失敗次數(shù)F為

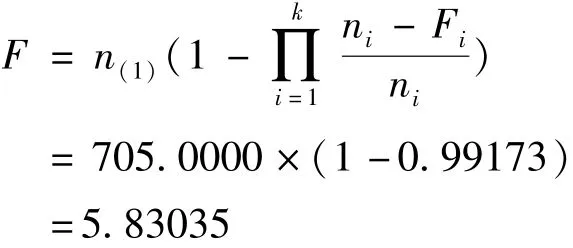
根據(jù)公式(11)、(12)得到

求解上述方程得到R1=0.98511,R2=0.98688。根據(jù)(F=6,R1=0.98511)和(F=5,R2=0.98688),采用線性插值法求得當(dāng)失效數(shù)F=5.83035時(shí),置信下限RL=0.98521。

4 總結(jié)

測量系統(tǒng)的性能可靠性和結(jié)構(gòu)可靠性是衡量測量系統(tǒng)的兩個(gè)重要的指標(biāo)。本文從性能可靠性和結(jié)構(gòu)可靠性兩個(gè)維度評定液體火箭發(fā)動(dòng)機(jī)試驗(yàn)流量測量系統(tǒng)可靠性。

1)根據(jù)試驗(yàn)任務(wù)書給出的流量上下限值,以及試驗(yàn)數(shù)據(jù)的分布特征,采用雙側(cè)性能可靠性方法,計(jì)算得到性能可靠性置信下限,得到性能可靠性的下限值為0.98529。雖然高于試驗(yàn)任務(wù)書對發(fā)動(dòng)機(jī)的可靠度要求(0.98000),但是還有較大的提升空間。

2)建立流量測量系統(tǒng)可靠性框圖以及串聯(lián)系統(tǒng)的特征,將流量測量系統(tǒng)組成單元中指數(shù)失效型數(shù)據(jù)轉(zhuǎn)換為成敗型失效數(shù)據(jù),采用L-M法和線性插值法計(jì)算得到系統(tǒng)結(jié)構(gòu)可靠性置信下限為0.98521。其結(jié)果雖然滿足要求,但是還存在較大的優(yōu)化余地。表2中的失敗次數(shù)和失敗的原因?yàn)樘岣邷y量系統(tǒng)結(jié)構(gòu)可靠性指明了方向。提高產(chǎn)品質(zhì)量、加強(qiáng)設(shè)備和零部件使用壽命的分析以及及時(shí)更換接插件等方法是有效提高結(jié)構(gòu)可靠性的手段。

綜上所述,雖然本文所采取的可靠性評估方法只得出了系統(tǒng)可靠性的近似解,但是針對測量系統(tǒng)的特殊性,上述評估方法對行業(yè)內(nèi)測量技術(shù)人員合理評價(jià)測量系統(tǒng)可靠性、研究提高系統(tǒng)可靠性方法提供了重要的參考。