汽輪發(fā)電機集電環(huán)機械設(shè)計計算

李 德，李志和，蘭 波，劉繼慧，李海龍

(1. 哈爾濱電機廠有限責任公司，黑龍江哈爾濱 150040；2. 哈爾濱大電機研究所，黑龍江哈爾濱 150040)

0 引言

集電環(huán)也稱滑環(huán)，是汽輪發(fā)電機關(guān)鍵部件之一，其與電刷、轉(zhuǎn)子繞組配合，起到提供電機旋轉(zhuǎn)磁場的作用。現(xiàn)今汽輪發(fā)電機集電環(huán)普遍采用通過絕緣套筒整體套裝在軸上的結(jié)構(gòu)方式，集電環(huán)、絕緣套筒與轉(zhuǎn)軸之間為典型過盈配合。發(fā)電機運行時，集電環(huán)既承受熱套過盈配合力的作用，同時又承受旋轉(zhuǎn)離心力的作用，受力情形較為復雜，故準確計算集電環(huán)機械應(yīng)力對其結(jié)構(gòu)設(shè)計具有重要的指導意義。資料顯示：熊東旭[1]對集電環(huán)的內(nèi)外徑、軸向尺寸與材質(zhì)，絕緣套筒厚度及配合緊量，集電環(huán)螺旋溝尺寸等問題給出設(shè)計建議；王迪等[2]基于有限元理論，采用ANSYS Workbench對1 000 MW汽輪發(fā)電機集電環(huán)裝配應(yīng)力進行了三維仿真分析；汪耕等[3]就汽輪發(fā)電機集電環(huán)的材質(zhì)、套裝工藝、冷卻方式、電腐蝕等問題進行過深刻討論，在進行汽輪發(fā)電機集電環(huán)設(shè)計時還應(yīng)關(guān)注和避免集電環(huán)和電刷在發(fā)電機運行過程中的各類故障；史德利等[4]曾針對300 MW汽輪發(fā)電機集電環(huán)與電刷磨損發(fā)熱問題改進優(yōu)化了相關(guān)結(jié)構(gòu)；李賢明等[5]對發(fā)電機運行中電刷和集電環(huán)常見故障和處理方法也進行了系統(tǒng)的介紹。

本文基于經(jīng)典彈性力學理論對汽輪發(fā)電機集電環(huán)、絕緣套筒與轉(zhuǎn)軸過盈配合變形協(xié)調(diào)方程進行了推導，計算了靜止、額定、超速三種工況下的集電環(huán)應(yīng)力與分離轉(zhuǎn)速，并與ANSYS Workbench非線性接觸仿真結(jié)果進行對比，以驗證本文所推導的集電環(huán)機械設(shè)計計算方法的有效性。

1 集電環(huán)裝配變形協(xié)調(diào)方程推導

1.1 集電環(huán)裝配結(jié)構(gòu)簡化

汽輪發(fā)電機典型的轉(zhuǎn)軸-絕緣套筒-集電環(huán)裝配結(jié)構(gòu)剖面見圖1。集電環(huán)包含正負兩環(huán)，由高質(zhì)量合金鋼制成，熱套在經(jīng)絕緣處理的套筒上。為保證有效通風冷卻和去除粉塵，集電環(huán)外表面開有螺旋形溝槽，內(nèi)部開有軸向、斜向通風孔，且常在兩個集電環(huán)之間的軸上安裝風扇裝置，以降低由勵磁電流引起的溫升。

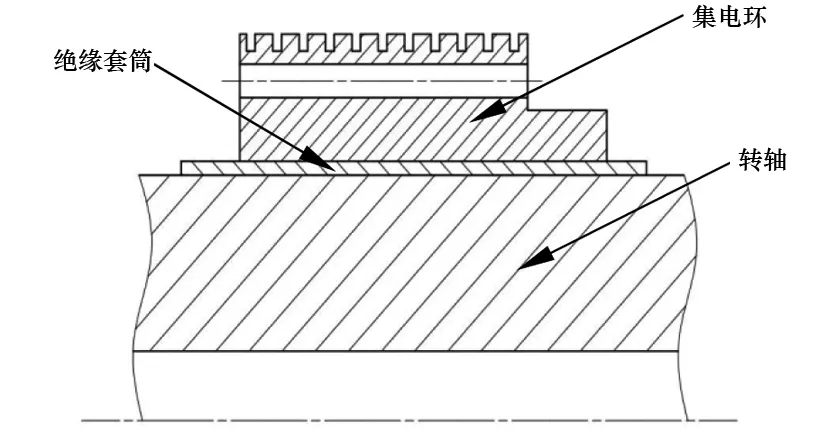
圖1 集電環(huán)裝配結(jié)構(gòu)示意

在汽輪發(fā)電機運行狀態(tài)下，集電環(huán)既承受自身旋轉(zhuǎn)的機械離心力、又承受過盈配合力的作用。本文對集電環(huán)機械計算進行推導時不計集電環(huán)表面螺旋溝槽與通風孔的影響，將集電環(huán)裝配簡化為圓筒式結(jié)構(gòu)，簡化后的轉(zhuǎn)軸-絕緣套筒-集電環(huán)裝配結(jié)構(gòu)見圖2。圖中，Li為絕緣套筒長度，Lc為集電環(huán)長度，D0為轉(zhuǎn)軸內(nèi)徑，Dsi為轉(zhuǎn)軸與絕緣套筒配合直徑，Dic為絕緣套筒與集電環(huán)配合直徑，Dc為集電環(huán)外徑。各部件材料屬性見表1。

表1 集電環(huán)裝配材料屬性

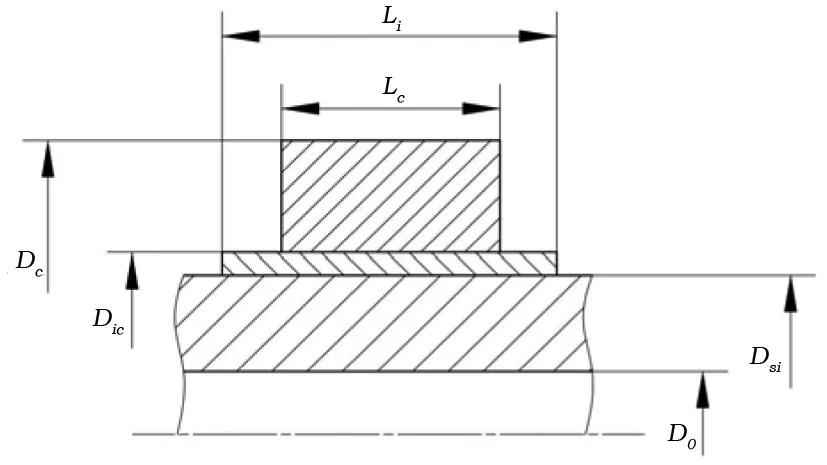
圖2 集電環(huán)裝配結(jié)構(gòu)簡化

集電環(huán)熱套安裝完成后，轉(zhuǎn)軸可視作承受外壓作用的圓筒模型，集電環(huán)可視作承受內(nèi)壓作用的圓筒模型，而絕緣套筒則可視作同時承受內(nèi)壓和外壓作用的圓筒模型。基于彈性力學理論[6]，內(nèi)半徑為a，外半徑為b的圓筒承受內(nèi)壓Pi和外壓Pe時的位移表達式為：

(1)

內(nèi)半徑為a，外半徑為b的等厚圓盤旋轉(zhuǎn)工況下的位移表達式為：

(2)

式中：ω為角速度；a≤r≤b。

聯(lián)立式(1)、式(2)可推導出轉(zhuǎn)軸、絕緣套筒、集電環(huán)承受過盈配合及機械旋轉(zhuǎn)作用下的變形和柔度。

1.2 集電環(huán)裝配變形和柔度推導

由1.1節(jié)可知，考慮集電環(huán)承受內(nèi)壓P1情況，令Pi=P1，Pe=0，a=Dic/2，b=Dc/2，代入式(1)，則集電環(huán)內(nèi)徑變形量為：

(3)

(4)

式中：Q1為集電環(huán)與絕緣套筒配合力。

根據(jù)柔度定義，可求得集電環(huán)柔度為：

(5)

考慮集電環(huán)以角速度ω旋轉(zhuǎn)時，令a=Dic/2，b=Dc/2，代入式(2)，則其內(nèi)徑變形量為：

(6)

同理，也可推導出轉(zhuǎn)軸與絕緣套筒的變形及柔度表達式。為簡化書寫格式及便于計算，現(xiàn)引入如下無量綱系數(shù)：

(7)

(8)

令轉(zhuǎn)速n=1 000 r/min，將表1材料屬性代入式(5)、式(6)，整理，可求得集電環(huán)柔度為：

(9)

集電環(huán)變形系數(shù)為：

(10)

內(nèi)徑處配合力引起絕緣套筒內(nèi)徑柔度為：

(11)

外徑處配合力引起絕緣套筒內(nèi)徑柔度為：

(12)

內(nèi)徑處配合力引起絕緣套筒外徑柔度為：

(13)

外徑處配合力引起絕緣套筒外徑柔度為：

(14)

絕緣套筒外徑變形系數(shù)為：

(15)

絕緣套筒內(nèi)徑變形系數(shù)為：

(16)

轉(zhuǎn)軸柔度為：

(17)

式中：ξ為考慮轉(zhuǎn)軸外伸端對柔度影響而進行修正的系數(shù)。

轉(zhuǎn)軸變形系數(shù)為：

(18)

根據(jù)式(10)、(15)、(16)、(18)，可進行集電環(huán)裝配配合緊量的初步計算及選取，集電環(huán)與絕緣套筒之間配合緊量初值計算公式為：

(19)

(20)

式中：np為超速轉(zhuǎn)速。

在進行緊量設(shè)計時，需綜合考慮集電環(huán)裝配的應(yīng)力及變形問題，既要保證各種工況下集電環(huán)應(yīng)力滿足強度要求，又要保證在超速工況下集電環(huán)裝配各部件不發(fā)生脫離或松動。

1.3 集電環(huán)裝配變形協(xié)調(diào)方程

綜上，根據(jù)集電環(huán)裝配受載及接觸變形情況，獲得集電環(huán)裝配變形協(xié)調(diào)方程為：

(21)

式中：Q1為集電環(huán)與絕緣套筒配合力；Q2為絕緣套筒與轉(zhuǎn)軸配合力；δci為集電環(huán)與絕緣套筒之間的設(shè)計緊量；δis為絕緣套筒與轉(zhuǎn)軸之間的設(shè)計緊量。

方程(21)為二元一次線性方程組，其表征了集電環(huán)裝配受熱套過盈及旋轉(zhuǎn)離心力作用下的變形關(guān)系。根據(jù)方程(21)，求解配合力Q1、Q2，從而計算集電環(huán)內(nèi)徑位置的環(huán)向應(yīng)力為：

(22)

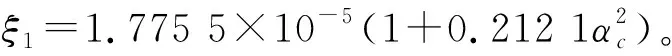
由式(22)可看出，式中右邊第一項為熱套配合作用產(chǎn)生的應(yīng)力分量，第二項則為旋轉(zhuǎn)機械作用引起的應(yīng)力分量。

根據(jù)方程組(21)，亦可求得在設(shè)計緊量狀態(tài)下轉(zhuǎn)軸-絕緣套筒-集電環(huán)的分離轉(zhuǎn)速，令Q1=0，消元，求得絕緣套筒與轉(zhuǎn)軸分離轉(zhuǎn)速表達式為：

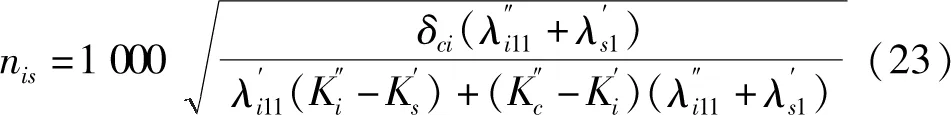
同理，令Q2=0，消元，求得集電環(huán)與絕緣套筒分離轉(zhuǎn)速表達式為：

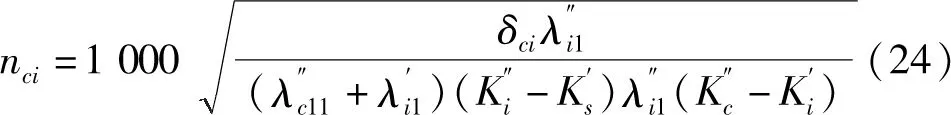
2 算例及有效性驗證

基于本文推導的集電環(huán)機械設(shè)計計算方法，選取某一產(chǎn)品發(fā)電機集電環(huán)軸段作為算例，計算該集電環(huán)在靜止、額定、超速三種工況下的最大環(huán)向應(yīng)力及分離轉(zhuǎn)速。為驗證該計算方法的有效性，采用ANSYS Workbench建立了集電環(huán)裝配二維接觸軸對稱模型，集電環(huán)與絕緣套筒、絕緣套筒與轉(zhuǎn)軸之間施加相應(yīng)的接觸設(shè)計緊量，并約束轉(zhuǎn)軸端面軸向位移。對于分離轉(zhuǎn)速的仿真，是通過漸進式提高轉(zhuǎn)速，觀測模型的接觸壓力分布狀態(tài)來判斷，當接觸壓力接近于0時可認為接觸失效，集電環(huán)裝配發(fā)生分離。有限元仿真結(jié)果應(yīng)力平均值為集電環(huán)內(nèi)徑位置的路徑應(yīng)力，理論計算和有限元仿真結(jié)果見表2。靜止、額定、超速三種工況下集電環(huán)裝配環(huán)向應(yīng)力及徑向位移分布見圖3、圖4。

圖3 集電環(huán)裝配環(huán)向應(yīng)力分布

圖4 集電環(huán)裝配徑向位移分布

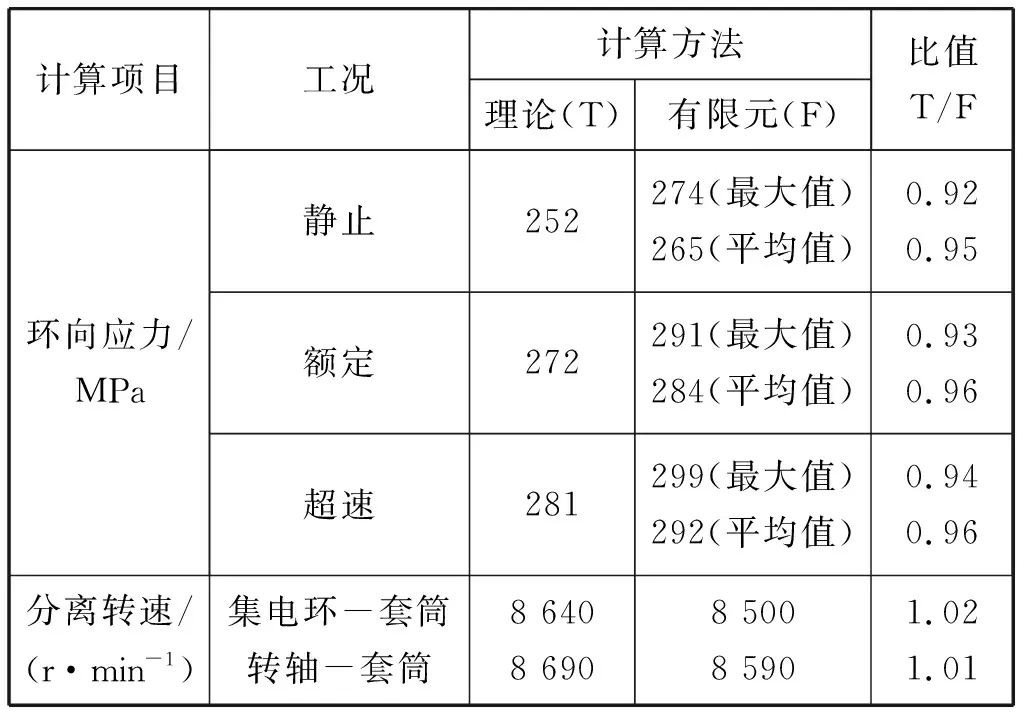
表2 集電環(huán)裝配計算結(jié)果匯總

由表2可知，集電環(huán)裝配理論計算與有限元仿真結(jié)果吻合較好，表明了本文推導的集電環(huán)機械設(shè)計計算方法的有效性，集電環(huán)最大環(huán)向拉應(yīng)力位于集電環(huán)內(nèi)徑位置。有限元仿真應(yīng)力普遍高于理論計算結(jié)果，其原因在于有限元仿真可有效模擬因剛度差異引起的絕緣套筒徑向變形的不均勻性，這種變形不均勻性使得集電環(huán)最大環(huán)向拉應(yīng)力位置出現(xiàn)在集電環(huán)內(nèi)徑端部，這是理論計算所不能計及的。與有限元方法相比，本文推導的集電環(huán)理論計算方法更為高效和便捷，特別適用于集電環(huán)結(jié)構(gòu)初步設(shè)計階段。

3 結(jié)論

基于經(jīng)典彈性力學理論，本文系統(tǒng)地推導了汽輪發(fā)電機集電環(huán)機械設(shè)計計算過程并計算了不同工況下的集電環(huán)機械應(yīng)力及分離轉(zhuǎn)速。研究表明：集電環(huán)機械設(shè)計理論計算與ANSYS Workbench有限元接觸非線性仿真結(jié)果吻合較好，本文推導的理論計算方法可有效用于汽輪發(fā)電機集電環(huán)的機械設(shè)計。