不同支撐體系下的矮塔斜拉橋線形參數分析

阮猛　李鵬飛　王之強

【摘 要】文章以某大跨度矮塔斜拉橋為研究對象，分別選取塔墩梁全固結，墩梁分離、墩塔固結，塔梁固結、塔墩分離三種不同支撐體系進行線形敏感參數研究，探究主梁剛度及容重、斜拉索剛度及容重、預應力張拉力、溫度效應對不同支撐體系下的線形影響程度。結果表明：塔墩梁全固結體系對溫度影響最為敏感，其余兩種體系對主梁容重最為敏感。主梁容重、預應力張拉力、溫度是影響線形的關鍵控制參數，主梁剛度、斜拉索剛度及容重則對線形的影響較小。

【關鍵詞】矮塔斜拉橋; 支撐體系; 線形; 敏感性分析

【中圖分類號】U448.27【文獻標志碼】A

矮塔斜拉橋是介于連續梁與斜拉橋之間的一種橋型，具有剛度大、跨越能力強等優勢，在我國得到了廣泛應用[1-2]。在矮塔斜拉橋建設時，因為施工現場環境復雜多變，結構參數與設計參數容易出現偏差，因此，準確把握橋梁結構變化規律，找尋關鍵控制參數，是矮塔斜拉橋施工控制的重要任務[3-4]。同時，在橋梁設計時，為了滿足抗震性能的要求，往往會對邊界結構進行調整，從而對橋梁關鍵控制參數產生影響[5]。因此，本文針對不同支撐體系的矮塔斜拉橋進行分析，分別建立3種體系的有限元模型。考慮主梁剛度及容重、斜拉索剛度及容重、預應力荷載、溫度這些參數的影響，探究結構參數變化對不同支撐體系下的矮塔斜拉橋的線形影響程度，找尋關鍵控制參數，從而為類似工程提供參考。

1 工程概況與有限元模型

1.1 工程概況

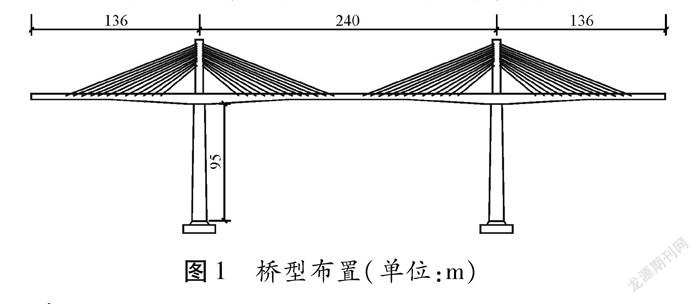
本文以某3跨矮塔斜拉橋為分析對象，對其進行不同支撐體系下的參數敏感性分析。橋梁全長512 m，布置形式如圖1所示。其中，主梁為變截面預應力混凝土箱梁，設置三向預應力體系，主梁高度4～8.2 m，采用二次拋物線變化。橋塔采用矩形空心橋塔。橋墩采用矩形實心斷面，最大墩高95 m。斜拉橋采用扇形布置，共采用48對斜拉索，索間距7 m。

1.2 有限元模型與比較體系

采用MIDAS軟件進行建模分析，主梁、橋墩均采用梁單元進行模擬，斜拉橋采用桁架單元模擬。全橋共建立526個單元和368個節點，有限元模型如圖2所示。

為了考慮不同支撐體系的影響，分別選取塔墩梁固結（體系1），墩梁分離、墩塔固結（體系2），塔梁固結、塔墩分離（體系3），這3種支撐體系進行比較分析，并對其邊界條件進行模擬。邊界條件模擬方法見表1所示。

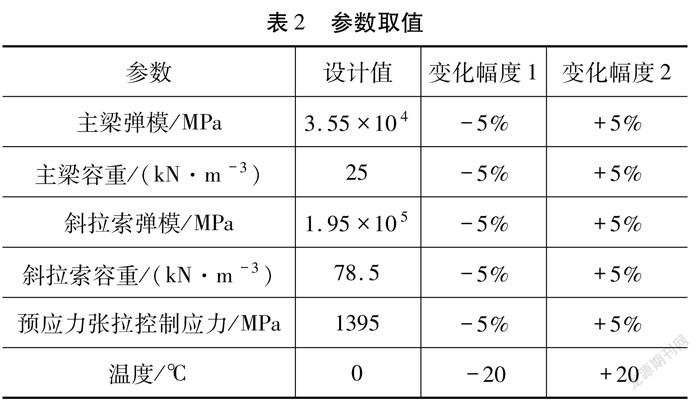
為了探究參數變化的影響，分別選取主梁彈模、主梁容重、斜拉索彈模、斜拉索容重、預應力荷載、溫度這六個參數進行分析。并選取在各自設計參數的基礎上，增加5 %與減少5 %這兩個變化幅度進行分析，分別計算這兩個變化幅度下橋梁撓度數值。結構參數取值見表2所示。

2 不同支撐體系下的結構參數敏感性分析

2.1 主梁剛度及容重

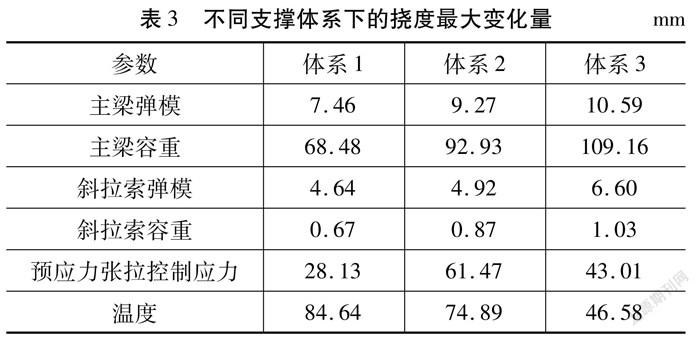
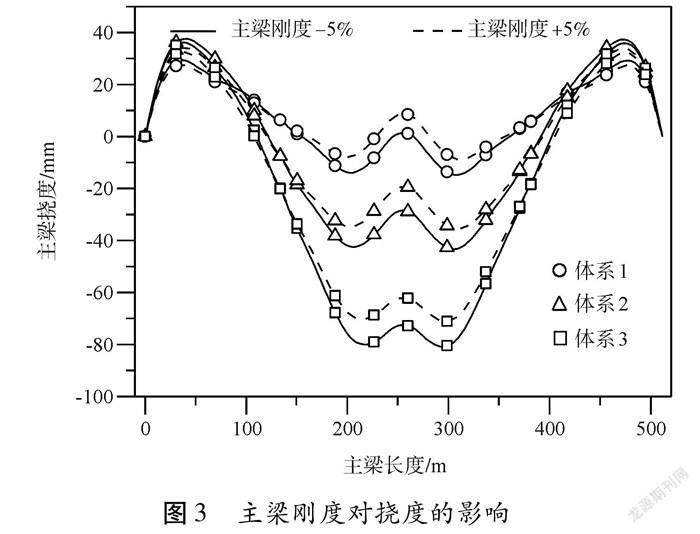
分別分析主梁剛度變化和容重變化對主梁撓度的影響。對主梁彈性模量進行改變，從而模擬主梁剛度變化。從圖3可以看出，在3中支撐體系下，體系1即塔墩梁全固結體系下，主梁撓度隨著主梁剛度的變化其變化幅度最小;體系3即塔梁固結，塔墩分離體系下，主梁撓度隨著主梁剛度的變化其變化幅度最大。并且，對于不同的支撐體系，體系3具有最大的主梁撓度，同時對主梁剛度的變化也最敏感。

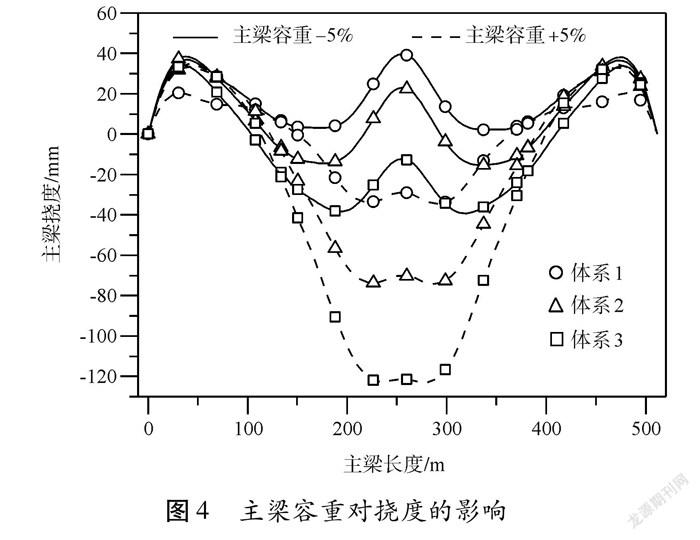
從圖4可以看出，在同一支撐體系下，主梁容重變化對主梁撓度的影響巨大，兩者最大差值達到109.16 mm。對于不同支撐體系，在體系3下主梁容重改變其對應的主梁撓度幅值變化最為明顯，故主梁容重對支撐體系3最為敏感。

2.2 斜拉索剛度及容重

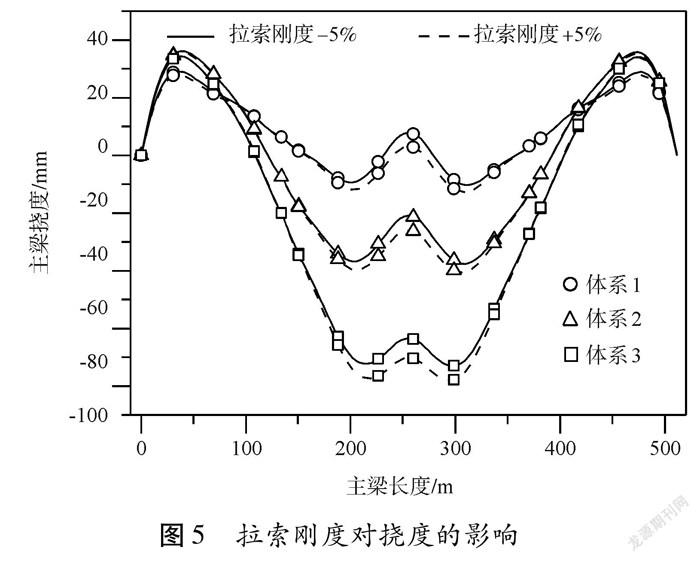
對拉索彈性模量進行改變，以模擬拉索剛度變化，從而探究斜拉橋剛度變化對主梁撓度的影響。從圖5可以看出，對于相同支撐體系下，斜拉索剛度變化對主梁撓度的影響很小，最大差值為6.6 mm。在不同支撐體系下，拉索剛度變化對主梁撓度的影響均較小，說明斜拉索剛度對主梁撓度的影響不顯著。

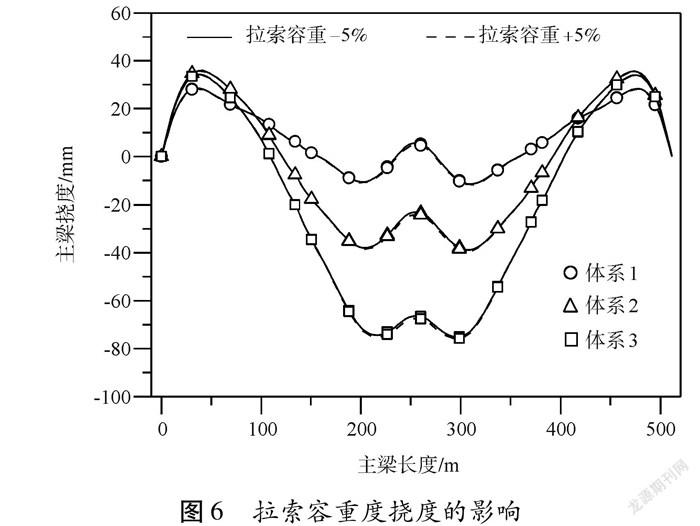
對斜拉索容重進行改變，探究其對主梁撓度的影響。如圖6所示，在不同支撐體系下，撓度隨著拉索容重的改變變化非常微小，因此表明拉索容重對線形的影響很小。這主要是因為斜拉索的重量占上部結構總重量的比例很小，因此影響微弱。

2.3 預應力效應

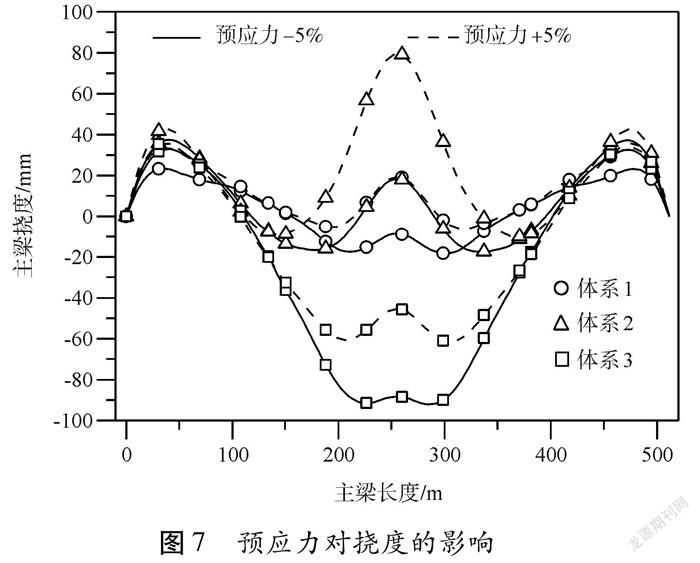
探究主梁預應力張拉力變化對主梁撓度的影響。從圖7可以看出，預應力改變在不同支撐體系下，對主梁撓度均有較大影響，最大變化幅度為61.47 mm，出現在體系2時。并且，對于同一支撐體系，從圖7可以看出，中跨撓度變化最為明顯，說明中跨線形控制極為重要。

2.4 溫度效應

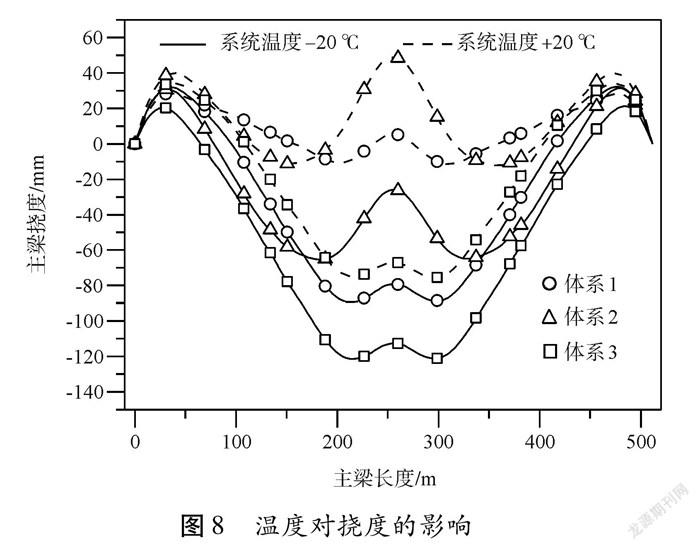
探究系統溫度改變對橋梁撓度的影響。從圖8可以看出，體系溫度變化對3種體系下的主梁撓度均有較大影響，最大撓度變化幅值為84.64 mm，發生在體系1中。同時，以上分析也可以說明，全固結體系對溫度的影響更為敏感，在施工控制中體系溫度的影響不可忽略。

2.5 參數敏感性分析

將以上各參數變化對主梁撓度的影響進行匯總，如表3所示。從表3可以看出，主梁容重、預應力荷載、溫度這三個參數對不同支撐體系下的主梁撓度均有較大的影響，這三個參數均可視為關鍵控制參數。其余參數對主梁撓度的影響較小，可視為不敏感參數。對于支撐體系1，主梁撓度對溫度的變化最為敏感，其次為主梁容重、預應力荷載、主梁彈模、主梁容重;對于支撐體系2，主梁撓度對主梁容重最為敏感，其次為溫度、預應力荷載、主梁彈模、斜拉索彈模;對于支撐體系3，主梁撓度對主梁容重最為敏感，其次為溫度、預應力荷載、主梁彈模、斜拉索彈模。

4 結論

本文針對矮塔斜拉橋結構參數特點，分別探究塔墩梁全固結，墩梁分離、墩塔固結，塔梁固結、塔墩分離，這三種支撐體系下的矮塔斜拉橋線形敏感參數，分析支撐體系對線形關鍵控制參數的影響。主要結論如下：

（1）主梁容重、預應力荷載、溫度對于主梁撓度變化最為敏感，是施工控制中的關鍵參數，而主梁剛度、斜拉索剛度及容重則對撓度的影響較小，其為次要敏感參數。

（2）不同支撐體系對主梁撓度的關鍵控制參數影響較大，對于塔墩梁全固結體系，撓度對溫度變化最為敏感;對于墩梁分離、墩塔固結與塔梁固結、塔墩分離體系，撓度對主梁容重變化最為敏感。

（3）在施工控制中，應特別注意混凝土超方，預應力張拉控制應力以及合龍溫度的影響，應該嚴格遵守設計值，控制模板變形量，預應力張拉量，從而減小線形誤差。

（4）對不同支撐體系下的矮塔斜拉橋，其關鍵控制參數具有較大差別，應注意橋梁支撐體系的影響，本文分析結果可為同類工程提出參考。

參考文獻

[1]劉榕， 伍英， 丁延書， 等. 多塔矮塔斜拉橋結構參數敏感性分析 [J]. 鐵道科學與工程學報， 2018， 15（5）： 1224-1230.

[2]王立峰， 姜洪偉， 崔海龍. 波形鋼腹板矮塔斜拉橋參數敏感性分析 [J]. 公路工程， 2015（2）： 117-121.

[3]周勇軍， 吳領領， 劉將， 等. 預應力混凝土矮塔斜拉橋線形敏感參數研究 [J]. 公路， 2020， 65（3）： 91-96.

[4]寇靜. 矮塔斜拉橋結構參數敏感性分析 [J]. 四川建筑， 2020， 40（3）： 159-162.

[5]劉士林， 王似舜. 斜拉橋設計 [M]. 北京：人民交通出版社， 2006.

[定稿日期]2021-01-26

[作者簡介]阮猛（1986～），男，本科，工程師，主要從事施工控制與管理工作;李鵬飛（1976～），男，本科，高級工程師，主要從事施工控制與管理工作;王之強（1975～），男，本科，高級工程師，主要從事施工控制與管理工作。