基于應變模態能檢測板狀結構內部損傷的模型建立

□□ 惠子君

(山西職業技術學院，山西 太原 030006)

引言

隨著科學技術的不斷發展，人們對產品質量的要求不斷提高。如交通方面，汽車、火車、飛機等各種交通工具為人們的出行提供了便利，但時有發生的交通事故也給人們的生命安全帶來了威脅。發生各種事故的重要誘因之一便是材料的疲勞負載。如何滿足人們對材料安全性的要求是相關科研人員面臨的新挑戰。如果能在不破壞被檢測件的前提下利用某項參數高效準確地檢測出隱藏于材料或結構中的損傷，從而及時采取相應的措施來補救，則可大大降低事故發生的可能性，保證人們的生命財產安全。

每種材料都有其固有屬性，如密度、質量、剛度、頻率與振型等。材料的振型是材料運動模式中的一種，在此運動模式下，每一部分都以同樣的頻率振動，形成如類正弦曲線一樣的波，每一個固有頻率對應一個振型。這些固有特性會由于損傷或是材料內部缺陷等而改變。當損傷或是缺陷產生時，材料的剛度會有所下降，柔度會增大。絕大多數的損傷探測法是基于材料的這些基本特性提出的，并且隨著時間的推移而不斷發展。

通常情況下，完整的損傷檢測包含四個階段：第一階段是檢測該材料是否存在損傷；第二階段是確定損傷的位置；第三階段是判定受損程度；第四階段是預估其殘余壽命。如何精確完整的獲取數據信息，并找到一個更加精準且能快速響應的指標參數是檢測的關鍵，通常使用參數β值來量化檢測損傷位置。

1 材料損傷檢測方法

損傷檢測的方法有好幾種，利用振動特性的信號來探測損傷的方法是目前最直觀、應用最廣的方法。振動特性可以用頻率、柔度以及應變模態等形式來表現，所以相應的損傷檢測法有基于固有頻率法、基于振型法、基于曲率法、基于殘余力向量法、基于組織柔性法和基于應變模態能法。

1.1 基于固有頻率法

在航空或橋梁的懸臂梁結構中多使用該法來測定材料內部損傷。固有頻率是材料最為直觀的振動特性，是最易被測得的一組信號。早在1969年，Lifshitz J M和Rotem A已經使用該方法來檢測材料結構中的損傷[1]。

該方法最為明顯的缺陷是材料的其他固有特性會在試驗過程中改變，且這些改變在檢測中會被忽略，比如材料損傷會引起質量的變化，而質量改變往往易被忽略。另一個缺陷是，材料中相同的頻率變化引起的原因有許多種，如一些特殊的結構特征也會引起頻率變化，不能簡單認為頻率的變化就是由材料缺陷而引起的[1]。可見，該方法對損傷位置的定位不夠靈敏和準確，所以逐漸被淘汰。

1.2 基于振型法

West W M是第一個使用振型置信度準則來檢測損傷的[2]。MAC模態置信度準則(modal assurance criterion)[3]和COMAC空間坐標模態置信度準則(coordinate modal assurance criterion)[4]都是在這一基本準則的前提下提出的。通過MAC和COMAC法計算出的β值介于0～1之間，使用該法可以近似地反映出結構的一些相關特性。然而，該方法在應用過程中也存在同樣的缺陷，對損傷的定位反映不夠靈敏，精準度還有待提高，致使該方法在應用上大大受限。

1.3 基于曲率法

材料的曲率是探測損傷的另一思路，因而基于振型曲率法也被用于測定材料的損傷[5]。該方法利用損傷狀態與完整狀態之間的絕對方差值的不同來確定損傷區域。材料受損后，損傷部位的剛度會下降，該區域的曲率會增大。與振型法相比，該方法對于材料損傷部位的定位較靈敏，但是，使用該方法需要具有嚴格的模態和采樣精度。

1.4 基于殘余力向量法

由楊秋偉、劉濟科教授首先提出，在檢測材料的損傷過程中，可以使用殘余力向量作為一個指標來探測損傷[6]。該方法引入了數值矩陣模型，準確地構造了質量矩陣和剛度矩陣。然而使用該方法時仍有一些不可避免的因素易被忽略，如結構質量及剛度的不均勻性會導致檢測結果存在一定的誤差。該方法在探測明顯裂紋的情況下效果甚好。

1.5 基于組織柔性法

當材料中存在1處不明顯裂紋時，質量矩陣和剛度矩陣的變化是不易察覺的。Pandey A K等是較早使用組織柔性變化來提高損傷位置探測精度的[7]。材料結構振動會產生撓度，撓度可使檢測方向更明確。該方法可以通過計算應變能來指示損傷位置，且經放大計算后可得到更大的數值，從而更好地用于模擬損傷位置。

1.6 基于應變模態能法

使用應變模態能來檢測結構損傷的方法已經日漸成熟，目前已經應用于檢測板狀結構和橋梁結構的損傷[8]。該法是在使用應變模態能作為指標參數的同時，輔助使用強大的矩陣來提高其計算精準度，且靈敏度高，是目前較為先進的探傷手段，優于以上幾種方法，因而在檢測中得到了廣泛使用。

最早研究是利用頻率來進行損傷測定，但外界的干擾對該方法的影響不可避免。隨著對精度要求的不斷提高，結合材料力學與固體力學等多重研究，發現應變模態能是當前最佳的定損指標。

2 基于應變模態能檢測板狀結構損傷的數學模型

板狀結構的自然屬性與代數計算之間有著相當密切的關系，可以使用大量的矩陣論來進行轉換模擬。對該結構損傷的檢測步驟是：首先，計算板的質量矩陣和剛度矩陣；其次，使用線性代數中的特征值和特征向量來模擬板狀結構的固有頻率和振型。根據特征值與特征向量一一對應的代數屬性，結合固有頻率與振型相互映射的特點，材料的固有頻率可用特征值來表征，而振型可以用與特征值相對應的特征向量來表示，則材料的固有頻率與振型可以利用代數矩陣進行轉化計算。圖1所示為被測板狀結構模型圖。

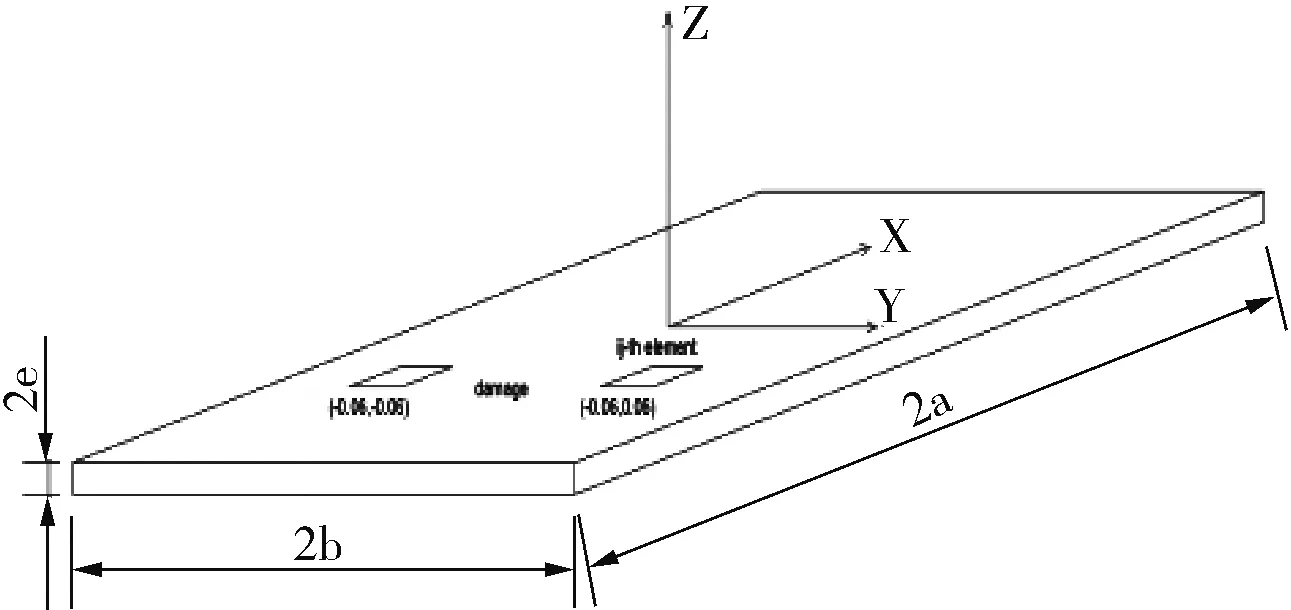
圖1 被測板狀結構模型圖

使用板件損傷部位的應變模態能與無損板件的應變模態能的比率來模擬反映被檢測部位的損傷情況。在模擬過程中，將板件細劃為均勻的小格，從而提高探傷精度。使用參數β值來量化檢測損傷位置，在式(1)中，即是使用損傷部位應變模態能與無損條件下的應變模態能的比率來反映[9]。

(1)

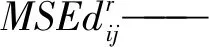
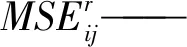
可以用式(2)來計算第r階模態下，第i行第j列對應小格的應變模態能[10]。

2(1-υ)(φ″r,ij)xy2)dxdy

(2)

式中：φr,ij——第i行第j列小格在第r階模態下的位移量；

(φ〃r,ij)x、(φ〃r,ij)y——在第r階模態下分別在x方向和y方向上的應變模態；

D——板的抗彎剛度；

v——該材料的泊松比。

與其他方法比較，基于應變模態能檢測板狀結構的內部損傷技術有明顯的優勢且備受關注。在該項技術中，通過不同的傳感器位置可獲取大量的試驗數據，傳感器位置的確定是一個重要環節，它是前期采集數據的關鍵，優化傳感器的位置及分布方式是優化過程中的研究方向之一。

優化指標參數是優化過程中的另一個研究方向，將收集到的數據經特定的算法可得到相對應的參數，損傷部位的參數值相較于完整無損傷部位的參數值會有明顯的差異，通過對比，可確定機構內部損傷位置。因此，在模擬仿真過程中，模擬圖像均成對出現，參數β模擬圖像如圖2所示，應變模態能模擬圖如圖3所示。

圖2 參數β模擬圖像

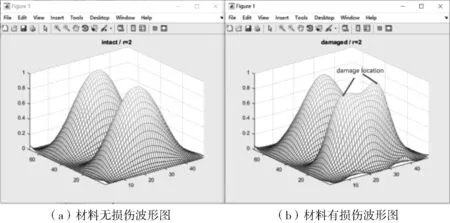
圖3 應變模態能模擬圖

由式(1)可看出，參數β包含了兩方面的信息，一個是應變模態能的收集，另一個是被測板件(可能存在損傷)與無損板件應變模態能之間的比值。為了能夠更精確地定位被測板件的損傷位置，盡可能提高指標參數β的指示作用，前期的數據采集工作至關重要。而傳感器位置的選擇與數據的采集息息相關，傳感器位置布置越合理，越能降低一些無關因素的干擾，減少極值誤差的產生。

3 結語

后三種方法較前三種方法在損傷定位的過程中更為有效，且其精準度也隨著矩陣的引入而大大提高。在今后的損傷檢測方法改進的過程中，通過改進算法提高損傷檢測精度仍是首要工作。

在后續的研究中，可將一些概率統計的內容融入到優化指標參數的過程中，對數據的分析將更加精準。同時，可將極大值或誤差值等小概率事件忽略，從而提高損傷檢測精度。