基于ANN 的加工零件表面粗糙度和能耗預測方法

肖小平，李晶晶，張超，周光輝，楊雄軍

1.湖南省計量檢測研究院，湖南 長沙 410014 2.西安交通大學 機械工程學院，陜西 西安 710049

隨著制造業自動化和智能化的快速發展，提高制造效率、降低成本和減少資源浪費成為各企業的共同目標。精準預測零件加工能耗與表面粗糙度(常用Ra表示)已成為當前智能車間綠色制造的主要研究熱點。目前對零件粗糙度和能耗的預測方法眾多，如正交試驗[1]、遺傳算法[2]、BP 神經網絡[3]、回歸模型[4-5]、支持向量機[6]等。上述關于粗糙度、能耗的預測模型大多將切削參數作為自變量，其他因素以系數方式影響計算結果。但在實際加工過程中，同一規格的刀具仍存在著因磨損狀況不同而導致的切削參數差異，其磨損狀況對粗糙度和能耗等有著不可忽視的影響。

ANN 因其在處理隨機數據、非線性數據等方面的自學習、自適應優勢而被廣泛應用于預測、分類等研究。Paturi 等[7]以切削參數為自變量，利用回歸模型和ANN 預測AISI 52 100 鋼硬車削過程中的表面粗糙度。Kant 等[8]結合實際加工實驗，研究了ANN 對能耗的預測能力。Gupta 等[9]提出了用ANN 和支持向量回歸相結合的車削參數優化方法。Sangwan[10]和Kumar 等[11]提出了一種將ANN 和遺傳算法相結合的方法對車削加工參數進行優化。從上述研究可以看出，使用ANN 模型考慮加工參數和加工性能之間的非線性關系，對預測實際加工過程中表面加工質量和切削能耗時，比傳統經驗模型更具優勢。基于以上分析與思考，本文從切削過程出發，考慮實際切削過程中影響刀具磨損與切削條件的因素，以刀具后刀面磨損量和切削三要素為自變量，采用ANN 模型對能耗和表面粗糙度進行預測，通過與回歸模型進行實驗對比，分析ANN 模型的優越性，據此擴展切削能耗的預測方法，為研究和踐行智能車間低碳制造提供理論和方法指導。

1 基于ANN 的粗糙度和能耗預測

1.1 粗糙度和能耗預測模型

本文以刀具后刀面磨損量和切削三要素為輸入，采用ANN 構建了零件加工能耗和表面粗糙度在線預測模型，如圖1 所示。

圖1 粗糙度和切削比能預測的ANN 結構

ANN 為該模型的核心，其結構主要包括輸入層、輸出層、隱含層及各層的神經元。輸入層和輸出層主要依據樣本數據來設定。其中，自變量為刀具切削速度、進給量、切削深度和后刀面磨損量，故輸入層應包含4 個神經元。同理，因變量為粗糙度和切削比能，因此輸出層包含2 個神經元。由于輸入變量和預測變量較少，且樣本數據量也較少，為避免由于網絡結構過于簡單而造成較大的誤差，在ANN 中設置2 層隱含層。

1.2 ANN 的參數設計

由ANN 結構可知，輸入層包含4 個神經元即M=4，輸出層包含2 個神經元即N=2，隱含層數為2。隱含層中神經元的數目會對網絡的收斂速度和穩定性產生巨大影響：神經元數目過少，則導致網絡對切削比能和粗糙度的預測準確率低，達不到預定的目標；而較多的神經元則會增加ANN 復雜度和降低其穩定性。當前常用試湊法或經驗法來確定中間隱含層中所包含的神經元數目，廣泛使用的經驗公式[12]如下：

式中：Li為隱含層所包含的神經元數，m為輸入層中所包含的神經元數，n為預測層中所包含的神經元數，a為0～10的正整數。

通過式(1)只能確定隱含層神經元數目的大致范圍，要想得到精確的神經元數還需通過實際數據對網絡進行訓練，進一步比較選出最優的隱含層神經元數目。選取不同數量的神經元在相同環境下對ANN 進行訓練并比較其輸出誤差值，進而選出最優的ANN 結構，如圖2 所示。

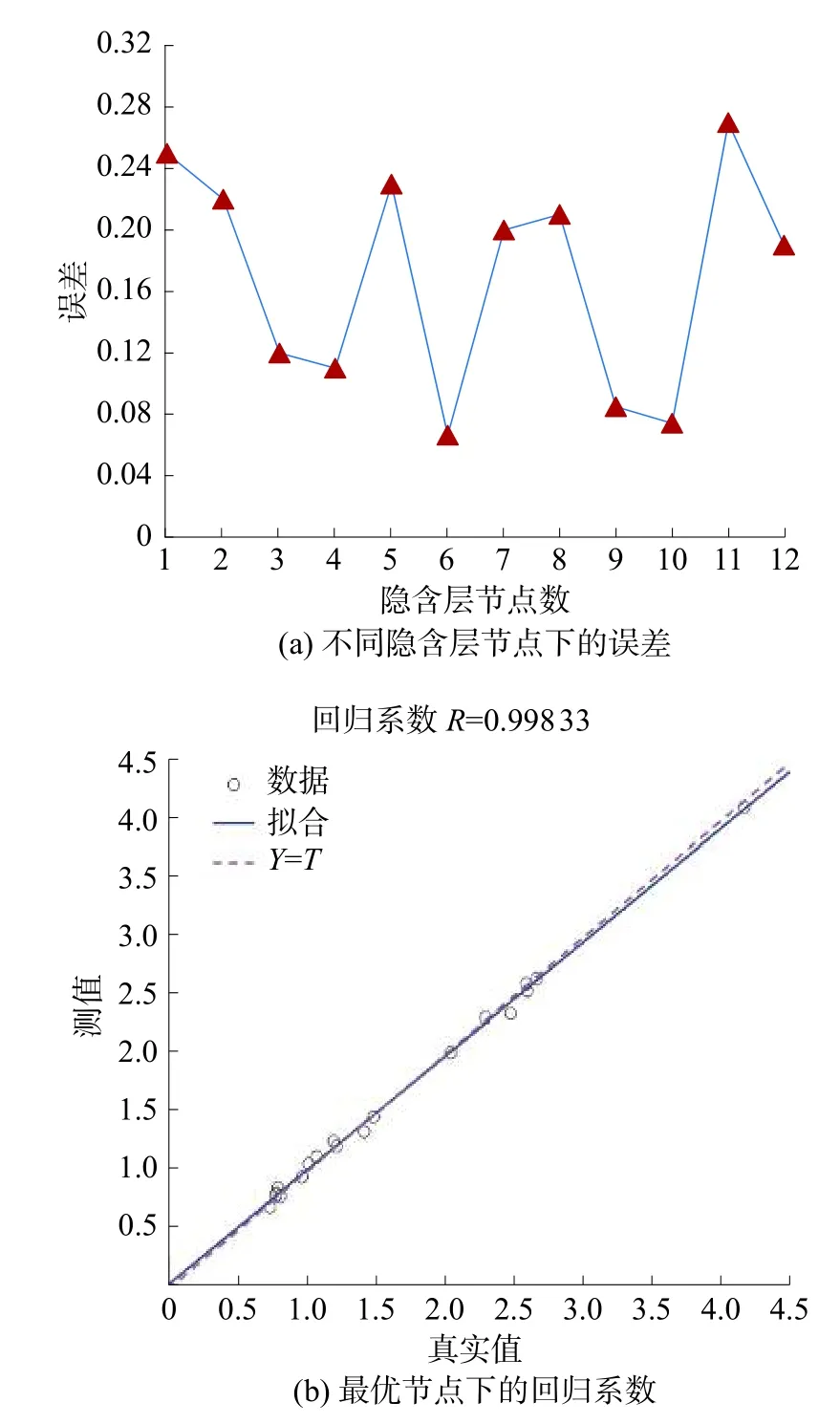
圖2 隱含層節點的選擇

由圖2 可知，當2 個隱含層皆由6 個神經元組成時，驗證集數據的平均絕對誤差最小，訓練數據集的回歸系數為0.99833，接近1，說明實驗結果與預測結果具有很強的相關性。因此，確定4-6-6-2 結構為最優的ANN 模型。

學習率是影響ANN 預測結果的一個關鍵變量。學習率過小會致使網絡的收斂速度降低；相反，較大的學習率可能會造成ANN 很難收斂。因此，訓練過程中需要不斷調整學習率以使網絡的準確率最高，經過多次試驗，最終學習率取0.002，動量系數取0.8，網絡中的學習算法如下：

式中：xk為權值參數矩陣，α為網絡的學習率，β為動量變量的系數，gk為ANN 中的學習函數梯度。

1.3 ANN 函數的選擇

1.3.1 傳遞函數

ANN 層與層之間通過傳遞函數進行聯系，經過多次對ANN 進行訓練發現，輸入層到第一個隱含層、第一個隱含層到第二個隱含層以及第二個隱含層到最終預測層的傳遞函數分別選擇線性函數、對數函數和線性函數。

1.3.2 優化函數

ANN 的訓練過程包括正向傳遞過程和反饋傳遞過程，傳遞過程中根據訓練誤差的大小通過優化函數不斷調整網絡各個節點的權值，以使網絡的精度最高。常用的優化函數有梯度下降法、牛頓法、變學習率反向傳播(back propagation,BP)算法和動量BP 算法[13-14](traingdm 函數)等。在本文中采用動量BP 算法traingdm 作為優化函數。

2 樣本數據集構建

2.1 樣本集構建及歸一化方法

本文以刀具后刀面磨損量和切削三要素為實驗變量，以粗糙度和切削比能為因變量的車削實驗數據作為訓練樣本。

由于訓練樣本的數量級和量綱不同，相互之間的差異較大，如若直接用于ANN 的訓練，將會導致較大的誤差，甚至可能無法獲得收斂的模型。因此，為了消除輸入樣本的數量級差異，將其無量綱化。在訓練樣本數據之前需對其執行歸一化操作，計算公式為

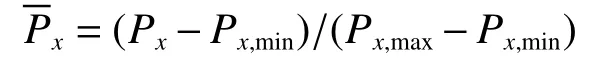
式中：Px為訓練樣本中的一組數據，Px,min為該組數據中的最小值，Px,max為該組數據中的最大值，為歸一化處理后的數據。

當對實驗數據進行預測后，需要對數據執行反歸一化操作才能夠使預測結果有實際的物理意義，計算公式為

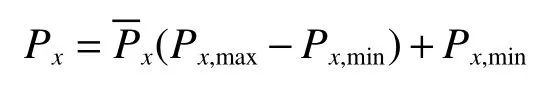
2.2 基于車削實驗的樣本數據集構建

1)車削實驗環境

為驗證提出的粗糙度和切削比能預測模型，在數控車床FTC20 進行車削實驗。車削實驗的刀片選用不同磨損程度的U6RW3862-R2-R1-P0，材料選用長度100 mm、直徑100 mm 的鑄鐵棒料。刀片的后刀面磨損量由激光共聚焦顯微鏡OLS4000 進行測量，表面粗糙度由高性能粗糙度儀TIME3221 進行測量，功率測量采用鉗式功率計PW3360 完成，如圖3 所示。

圖3 實驗使用機床、刀具及后刀面磨損測量圖

2)樣本數據集

在數控車床FTC20 上進行車削實驗。車削一共包含24 組實驗，隨機抽取第2、7、9、14 和21 組共5 組實驗數據作為驗證組，其余19 組作為擬合組，正交實驗水平如表1 所示。

表1 FTC20 車削實驗切削實驗水平表

切削比能(specific cutting energy，SCE)通常被定義為去除工件特定體積材料所消耗的切削能量，其值用ESC表示。SCE 可用于描述機床的能耗情況，能耗通過測量機床的功率來進行監測。為保證實驗的準確性，在同一組實驗下每測量5 次表面粗糙度值求一次平均值，每測量10 次功率值求一次平均值，獲得的實驗數據如表2 所示。

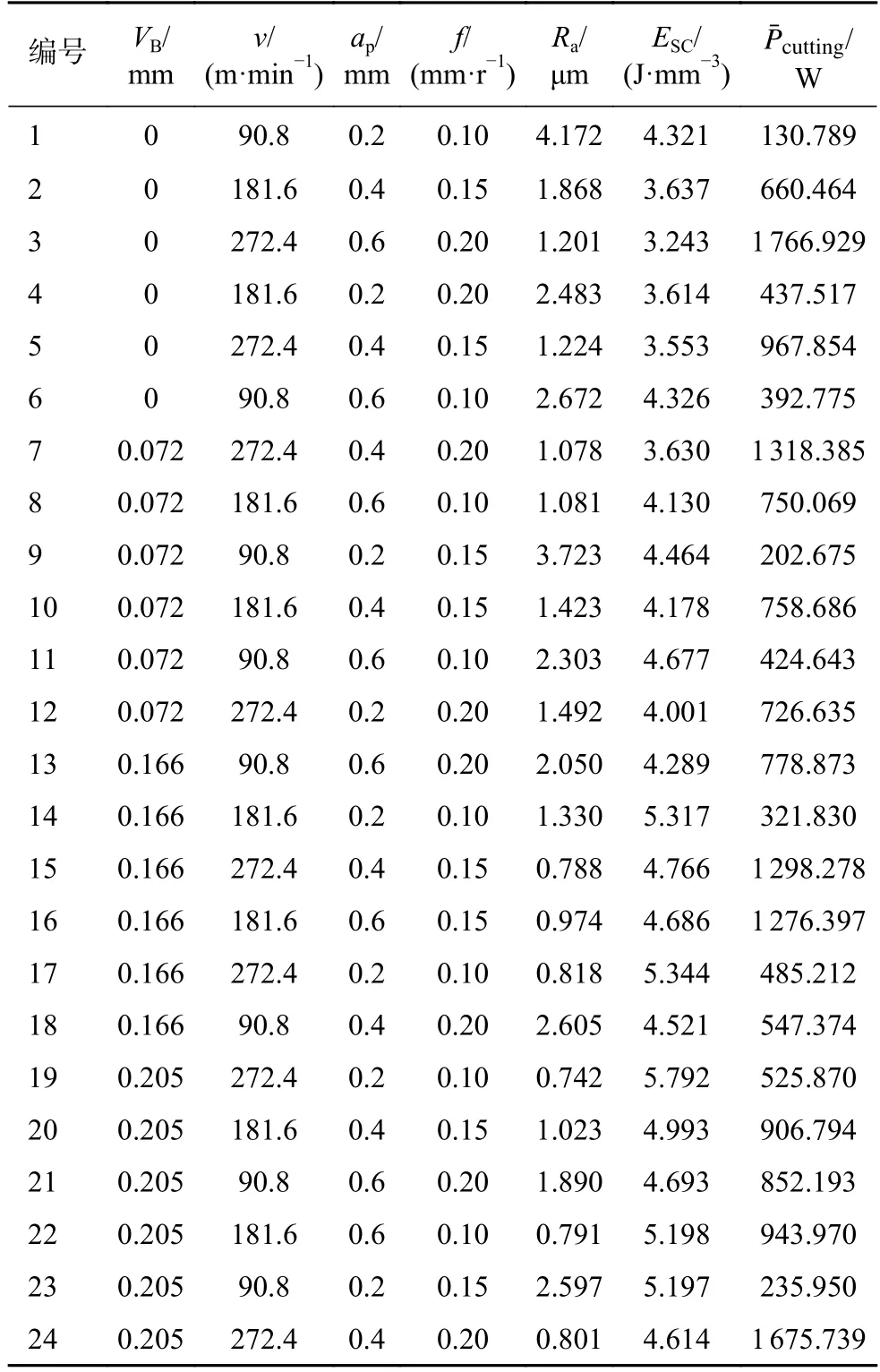
表2 實驗結果

3 案例研究

基于構建的樣本數據集，本節訓練得到了考慮刀具磨損的粗糙度和能耗預測模型，并通過與回歸模型預測方法進行對比，驗證了所提模型與方法的正確性和有效性。

3.1 基于ANN 的粗糙度和能耗預測模型訓練與應用

為了方便與回歸模型進行對比分析，同樣以樣本數據中的19 組實驗數據作為訓練集，另外5 組數據作為驗證集。

ANN 對Ra預測結果與實測值的比較如圖4所示。圖4(a)是在訓練組上ANN 預測值與實測值的比較情況，最大百分比誤差(maximum percentage error，MPE)值eMP為6.24%，平均絕對百分比誤差(mean absolute percentage error，MAPE)值eMAP為2.48%；在驗證組圖4(b)中，eMP為6.44%，eMAP為5.12%。采用ANN 的預測誤差值均在7%以內，說明了采用本文提出的ANN 結構能夠準確且有效地預測機床實際加工中的特征表面粗糙度，證明了本文提出的ANN 結構的合理性。

圖4 Ra 的ANN 預測結果與實測值對比

ANN 對切削比能的預測結果與實測值比較如圖5 所示。

圖5 ESC 的ANN 預測結果與實測值對比

圖5(a)是在訓練組上ANN 預測值與實測值的比較情況，eMP為6.38%，eMAP為2.65%；在驗證組圖5(b)中，eMP為3.31%，eMAP為1.66%。采用ANN 的預測誤差值均在7%以內，說明了采用本文提出的ANN 結構也能夠準確且有效地預測機床實際加工中的切削比能，進而實現能耗的有效預測，同樣證明本文提出的ANN 結構的合理性。

3.2 基于回歸模型的刀具磨損的粗糙度和能耗預測

基于刀具磨損建立表面粗糙度和切削功率的回歸模型(regression model，RM)[15-16]為

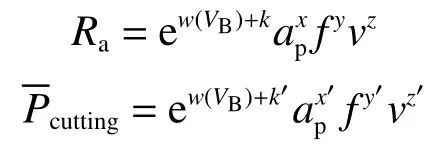
式中：Ra為表面粗糙度，mm；VB為后刀面磨損量，mm；k、k′為待定系數；ap為切削深度，mm；f為進給量，mm/r；v為切削速度，m/min；為切削功率，W；w、x、y、z、x′、y′和z′為待擬合系數。

根據文獻[17-18]得Esc的計算公式為

式中：Ecutting為切削過程消耗的能量，J；Q為材料去除體積，mm3；MRR為材料去除率，mm3/s；ESC為切削比能，J/mm3。

整理后得：

表面粗糙度和切削比能的回歸模型皆與刀具切削參數及后刀面磨損量等存在復雜的冪函數關系，因此，為方便進行實驗驗證，整理得：

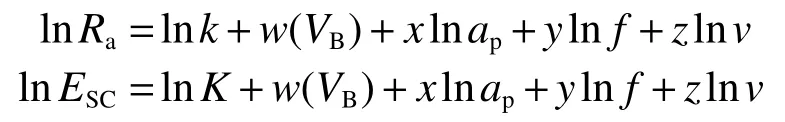
采用IBM SPSS Statistics 進行回歸處理得到回歸模型中的各個系數，獲得Ra的多元線性擬合分析結果如表3 所示。根據線性回歸分析，R2=0.99 ＞0.85，表明模型擬合情況良好。

表3 多元非線性擬合分析結果

因而得到的模型擬合公式如下：

通過對擬合數據的進一步分析判斷模型擬合的效果，給出FTC20 車削實驗中表面粗糙度的擬合效果及驗證組誤差百分比圖，如圖6 所示。

圖6 Ra 的擬合效果及驗證組誤差

圖6(a)給出的是回歸擬合粗糙度與實際實驗結果的比較情況，擬合組的eMP為6.47%，eMAP為2.98%；在圖6(b)驗證組中，eMP為6.70%，eMAP為3.43%。由此說明擬合誤差較小，效果理想。

同理，對切削比能也進行回歸和數據分析，R2=0.96 ＞0.85表明模型擬合情況良好。得到模型的擬合公式為

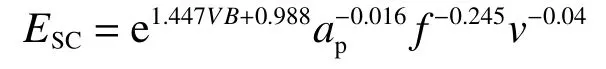
同樣通過對切削比能的擬合數據進一步分析來判斷模型擬合的效果，給出FTC20 車削實驗中切削比能的擬合效果及驗證組的誤差對比如圖7所示。

圖7 ESC 的擬合效果及驗證組誤差

圖7(a)給出的是回歸擬合切削比能與實際實驗結果的比較情況，擬合組中的eMP為6.62%，eMAP為2.25%；在圖7(b)驗證組中，eMP為4.50%，eMAP為1.92%。由此說明擬合誤差較小，效果理想。

3.3 模型驗證和性能分析

為了充分評價回歸模型(regression model,RM)和ANN 分別對表面粗糙度和切削比能的預測能力，將ANN 和回歸模型的預測結果與實測值進行對比，并計算了模型預測結果與實測值之間的絕對誤差百分比值。表面粗糙度實測值與模型預測結果對比如圖8 所示，詳細數據如表4所示。

圖8 Ra 的實測值與不同方法預測值對比

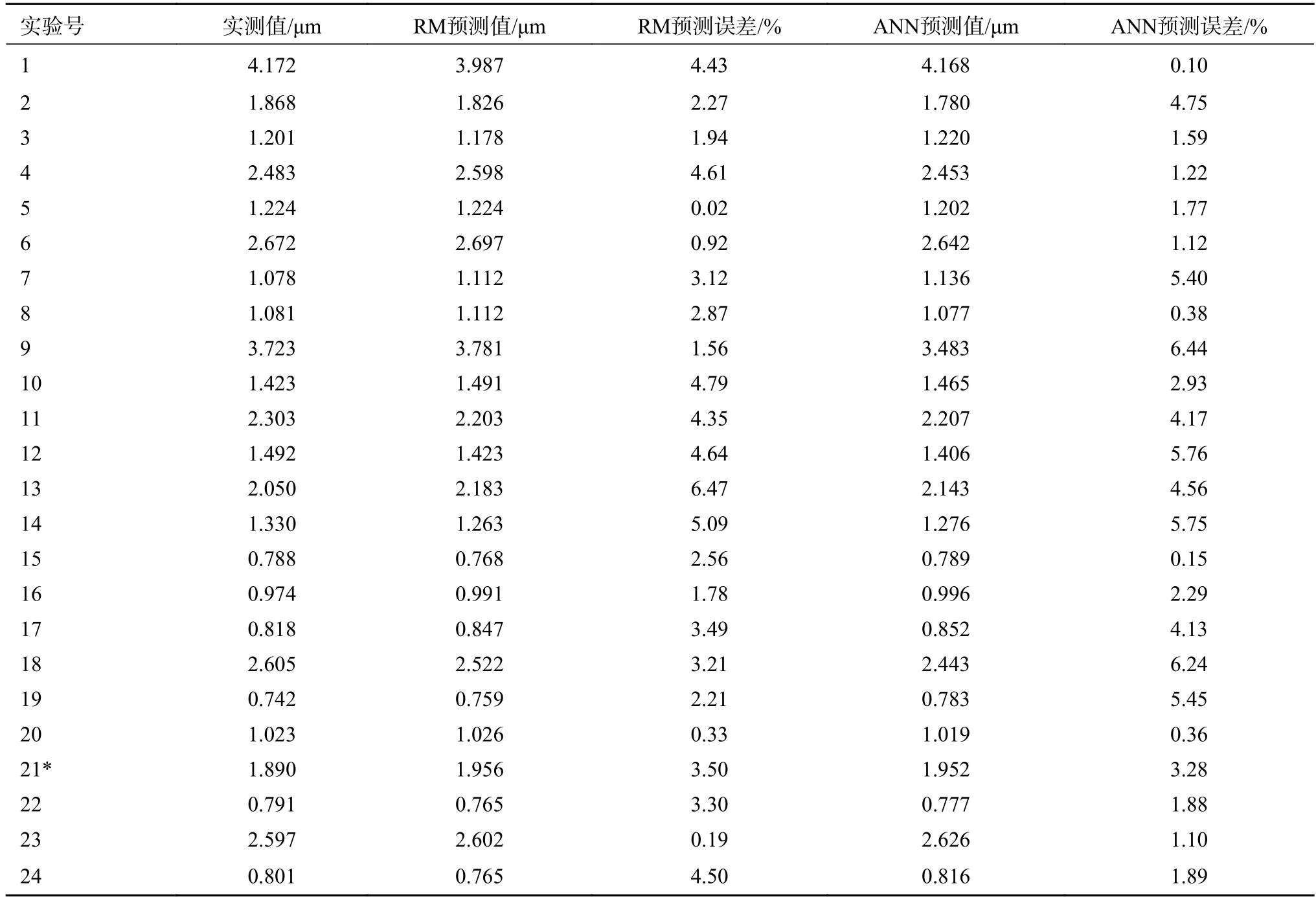
表4 Ra 的模型預測值與實驗實測值之間的絕對百分誤差

同理，對切削比能的實驗數據也進行了對比分析，如圖9 所示。

圖9 ESC 的實測值與不同方法預測值對比

在Ra驗證集上，RM 和ANN 的eMP分別為6.70%和6.44%。在ESC驗證集上，RM 和ANN 的eMP分別為3.50%和3.31%，eMAP分別為1.92%和1.66%。由此可以看出，2 種預測方法的預測結果都在可接受的誤差范圍內，均適用于對Ra和ESC進行預測。但是與RM 相比，ANN 的預測結果更接近實測值，預測效率更高。因此，選用ANN 進行Ra和ESC預測更準確。

4 結論

本文考慮了刀具后刀面磨損對切削比能和表面加工質量的影響，基于ANN 模型進行工件表面粗糙度和能耗預測，并通過與回歸模型對比，驗證了ANN 方法的優越性。

1)本文以刀具磨損對能耗和粗糙度預測的影響為考慮因素，從實際切削過程出發，以刀具后刀面磨損量和切削三要素為自變量，設計了基于ANN 的粗糙度和能耗預測模型，相較于傳統的預測模型更符合切削實際過程。

2)采用RM 和ANN 對能耗和表面粗糙度進行評估，通過實驗比較分析，在Ra和ESC驗證集上，ANN 的預測結果最大百分比誤差更接近實測值，相較于RM，ANN 對表面粗糙度和能耗的預測精度分別提升了5.4%和13.5%，驗證了ANN 模型在預測效率和預測精度上的優越性。