考慮延時補償的配電網柔直網側諧波電流抑制策略

朱海勇，吳小丹，董云龍，吳永華，劉 鵬，裘 鵬，戚宣威

（1.南京南瑞繼保電氣有限公司，南京 211102；2.國網浙江省電力有限公司電力科學研究院，杭州 310014）

0 引言

基于MMC-MVDC（模塊化多電平換流器中壓直流）的配電網系統以其靈活可控、不依賴交流電網、可隔離交流故障、易于分布式能源并網等特性，可實現配電網、多元能源及負荷的電能互聯，具備能量多向柔性控制、均衡負荷和連續負荷轉供，提升供電質量及可靠性的能力[1-4]。

隨著MMC-MVDC 的廣泛應用，其應用場景也多種多樣。非線性負載產生的諧波電流污染是電網主要電能質量問題之一，對電網安全運行產生嚴重危害并降低電能使用效率。MMC-MVDC本質上是電壓源型換流器，其經典的PI（比例-積分）控制器在基于旋轉坐標變換的矢量控制方案中可實現直流量的無靜差調節，實現有功功率、無功功率、直流電壓以及交流電壓控制。然而非線性負載產生的諧波電流頻率范圍較寬，PI 控制器高頻增益較低，不能滿足控制要求。PR（比例-諧振控制器）在諧振點處有無窮大增益，能無靜差地跟蹤諧波電流，是諧波治理的良好選擇。當前，網側諧波電流抑制方法主要集中在有源電力濾波器領域，文獻[5]提出了一種基于矢量諧振調節器的有源電力濾波器網側電流檢測控制方法，文獻[6]提出一種基于基波和諧波電流獨立的雙閉環控制結構的有源電力濾波器網側電流檢測控制方法。然而，MMC-MVDC 領域關于網側諧波電流抑制文獻較少。文獻[7]探討了直流配電網中直流側電能質量問題，文獻[8]對柔性直流配電網交流側不對稱故障進行研究，文獻[9]提出了基于諧振補償的MMC 網側低次諧波抑制方法。由于控制鏈路延時是造成柔性直流系統接入交流電網后引發高頻震蕩的重要原因[10-13]，因此，在考慮延時補償條件下，研究MMC-MVDC 諧波電流抑制策略具有重要意義和工程應用價值。

本文以MMC-MVDC 為研究對象，以諧波抑制和功率控制為研究目標，分析了基于控制鏈路延時補償的PR 控制器的網側電流閉環諧波抑制的原理。基于MATLAB 分析了功率控制環和諧波抑制環幅頻特性，并與傳統PR 控制器的諧波抑制穩定性進行對比。最后將該方案應用到三端柔直配電網系統，通過RTDS 仿真試驗，驗證了所提控制策略的正確性和有效性。

1 MMC-MVDC 系統結構和控制策略

三端柔直配電網系統結構如圖1 所示。三端交流系統通過三端背靠背柔直連接，實現交流系統合環。

圖1 三端MMC-MVDC 系統結構

以端口1 為例，分析網側電流閉環控制方法。圖2 為柔直系統端口1 接入交流電網的等效電路圖。

圖2 中usj（j=a，b，c）為交流系統的網側三相電壓，uvj為閥側三相電壓，isj為網側三相電流，ivj為閥側三相電流，iLj為網側非線性負載三相電流，ibpj、ibnj分別為上下橋臂的橋臂電流，udp、udn分別為正負極直流電壓，idp、idn分別為正負極直流電流，箭頭方向表明各個電流的正方向，L 為橋臂電感。

1.1 柔直系統功率控制系統結構

首先分析柔直系統數學模型。按照圖2 所示參考方向，忽略回路電阻，建立柔直與交流系統平衡運行方式下的網側電壓、閥側電流、閥側電壓表達式，如下所示：

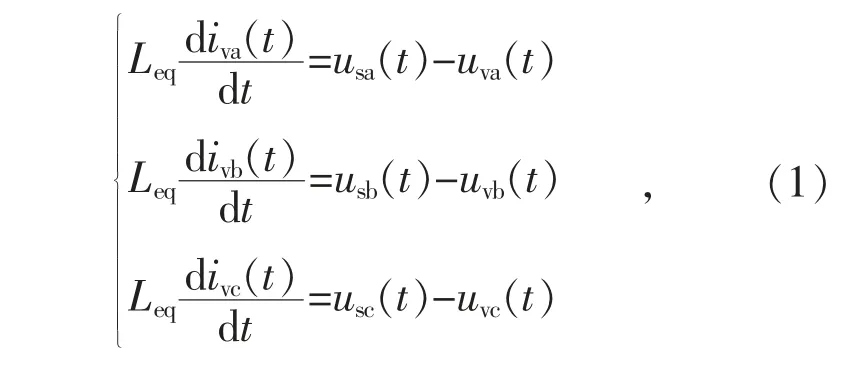
對式（1）進行dq 坐標變換，從而得到dq 坐標系下的電壓、電流表達式：

式中：ivd，ivq為閥側電流的d、q 軸分量；usd，usq為網側電壓的d、q 軸分量；uvd，uvq為閥側電壓的d、q 軸分量；ω 為角頻率。

根據公式（2），可以得到MMC 的電流控制框圖如圖3 所示。

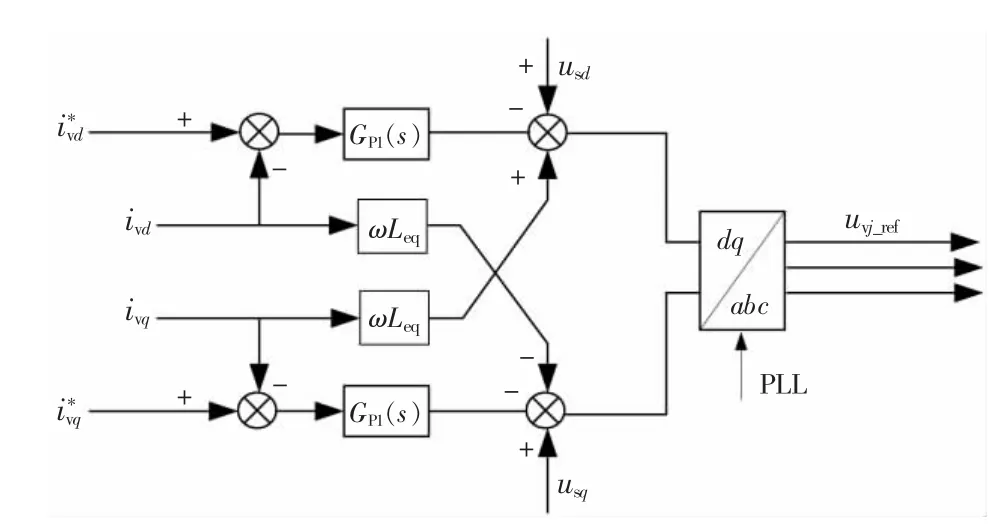
圖3 柔直系統電流控制框圖

1.2 網側諧波電流抑制系統結構

圖2 中非線性負載將在網側電流中引入諧波成分，對電能質量產生危害。MMC-MVDC 本質上是電壓源型換流器，其經典的PI 控制算法可在dq 坐標系中完成直流側電壓穩定和直流量指令跟隨，實現有功功率、無功功率、直流電壓以及交流電壓控制。然而非線性負載產生的諧波電流頻率范圍較寬，以5 次、7 次、11 次居多，傳統PI 控制器高頻增益較低，不能滿足控制要求。PR在諧振點處有無窮大增益，能無靜差跟蹤諧波電流，是諧波治理的良好選擇。使用PR 控制器做諧波控制時，在αβ 靜止坐標系中，無需鎖相環節并且無需對正負序諧波進行分離控制，可由一個諧振控制器同時控制正負序諧波。

由此基于網側諧波電流檢測的閉環PR 控制框圖如圖4 所示。在柔直系統電流內環疊加諧波抑制環節，以負載諧波電流為指令值，經過PR控制器，對5 次、7 次、11 次諧波無靜差跟蹤，由閥側電流ivj補償諧波電流，最終實現網側電流的諧波治理。圖中，分別為網側非線性負載電流α，β 軸分量指令值，簡稱諧波電流α，β 軸分量指令值，ivα，ivβ為閥側電流的α，β 軸分量，GH（s）為諧波抑制PR 控制器的傳遞函數。

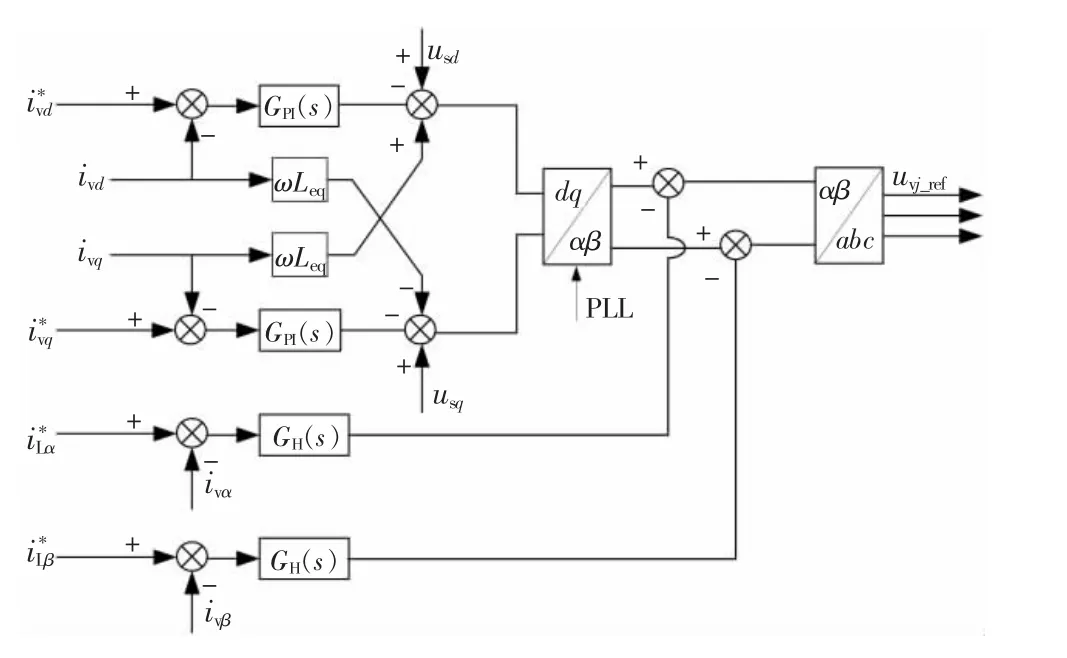
圖4 含網側諧波電流抑制的電流控制框圖

將圖4 轉化成圖5 MMC-MVDC 網側電流閉環控制策略。圖中為s 域下諧波電流αβ 坐標系下的指令值，為s 域下閥側電流dq 坐標系下的指令值，us為s 域下網側電壓，iv_abc為s 域下閥側abc 三相電流，GPI（s）為柔直系統功率控制環節PI 控制器的傳遞函數，GMMC（s）為被控對象的傳遞函數，GH（s）為諧波抑制PR 控制器的傳遞函數，Gd（s）為控制系統延時傳遞函數，KPWM為換流器輸出增益，本文取KPWM≈1。

圖5 MMC-MVDC 網側電流閉環控制策略

2 電流環控制器設計

2.1 具備延時補償的PR 控制器原理

MMC-MVDC 的受控對象可視為典型的阻感性負載，其在αβ 靜止坐標系下的傳遞函數可表示為[15]：

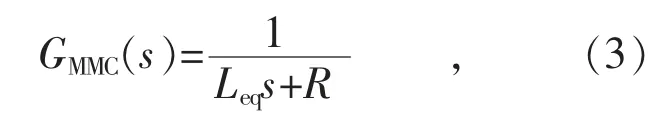
式中：Leq和R 分別為MMC-MVDC 連接電抗器的電感和等效電阻[16-17]。

在dq 旋轉坐標系中，正序及負序電流控制均可利用PI 控制器實現對電流的無靜差控制，PI 控制器由下式給出：

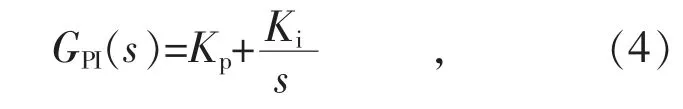
式中：Kp為比例系數，Ki為積分系數。在同步旋轉坐標系（dq）和靜止坐標系（αβ）中，通過卷積變換可以實現旋轉坐標系統下的PI 控制器向靜止坐標系統下的PR 控制器的轉換：

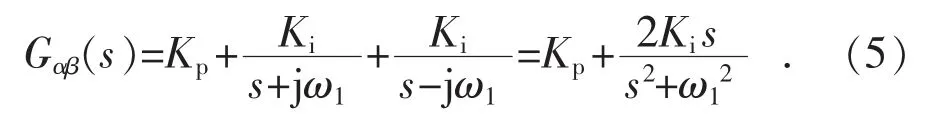
PR 控制器傳遞函數GPR（s）為：

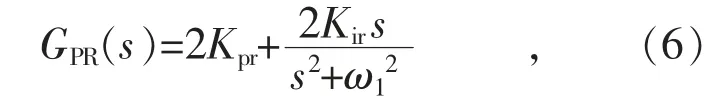
式中：Kpr和Kir為PR 控制器的比例系數和諧振系數；ω1為基波角頻率。

由于MMC-MVDC 控制鏈路延時在高頻段將給諧波控制帶來顯著的影響。為了降低系統延時在高頻段帶來的相位偏移影響，諧波抑制采用帶延時補償的PR 控制器[18]，因此式（5）需修改為：

工程應用中，為了獲得被控制諧波頻率處較大的控制效果，可以將完全諧振控制改為準諧振控制，對于多次諧波抑制，將PR 控制器并聯成組[18]，得到的諧波抑制控制器傳遞函數GH（s）為：

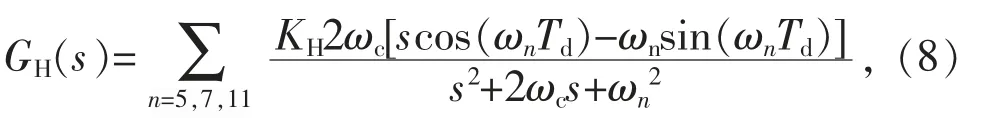
式中：KH為n 次諧波PR 控制器的諧振系數；ωn為n 次諧波角頻率；ωc為用于設計諧振控制器帶寬，一般取0.01ωn；Td為控制鏈路延時時間。

圖5 中的延時傳遞函數Gd（s），可采用二階派德等效近似表示為[17]：

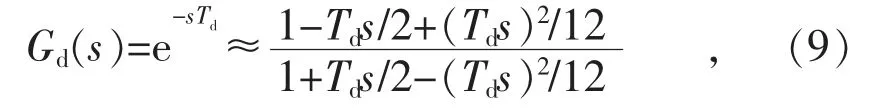
式中：Td=1.5T，T 為控制系統采樣周期。

2.2 穩定性分析

dq 坐標系中的PI 控制器等效為αβ 坐標系中的PR 控制器后，圖5 中坐標變化得到簡化，可全部統一至αβ 坐標系中，如圖6 所示。圖中為s 域下閥側電流αβ 坐標系下的指令值；iv_αβ為s 域下αβ 坐標系的閥側電流。

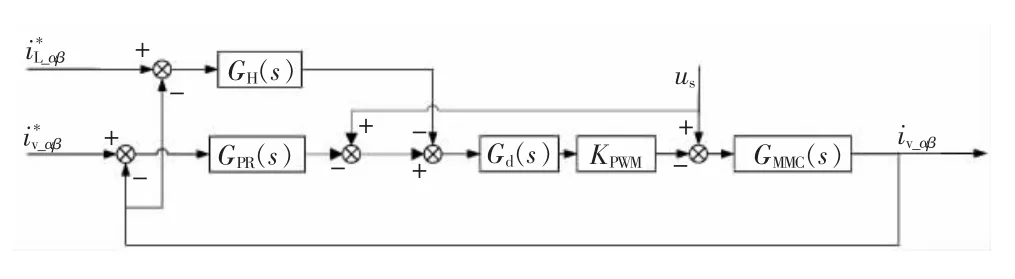
圖6 αβ 坐標系中MMC-MVDC 閉環諧振控制策略

根據疊加原理，圖6 可分為以有功無功功率電流指令為輸入的功率控制環和以負載電流變化為輸入的諧波控制環如圖7 所示。

圖7 簡化后的電流閉環諧振控制策略

其中，功率控制環和諧波控制環的開環傳遞函數分別為GH1（s），GH2（s）：

采 用MATLAB 繪 制GH1（s），GH2（s）的 伯 德圖。功率控制環開環傳遞函數GH1（s）的伯德圖如圖8（a）所示。幅頻曲線中，基波頻率處的增益很大，有利于減小功率控制穩態誤差，在諧波頻率處增益很小，對諧波抑制作用十分有限；相頻曲線中，相位裕度大于45°，滿足穩定性要求。

諧波控制環開環傳遞函數GH2（s）的伯德圖如圖8（b）所示。幅頻曲線中，基波頻率處的增益很小，避免了諧波控制環對基波的影響，在各諧波頻率處增益很大，有利于減小諧波控制穩態誤差；相頻曲線中，相位裕度大于90°，滿足穩定性要求[19]。

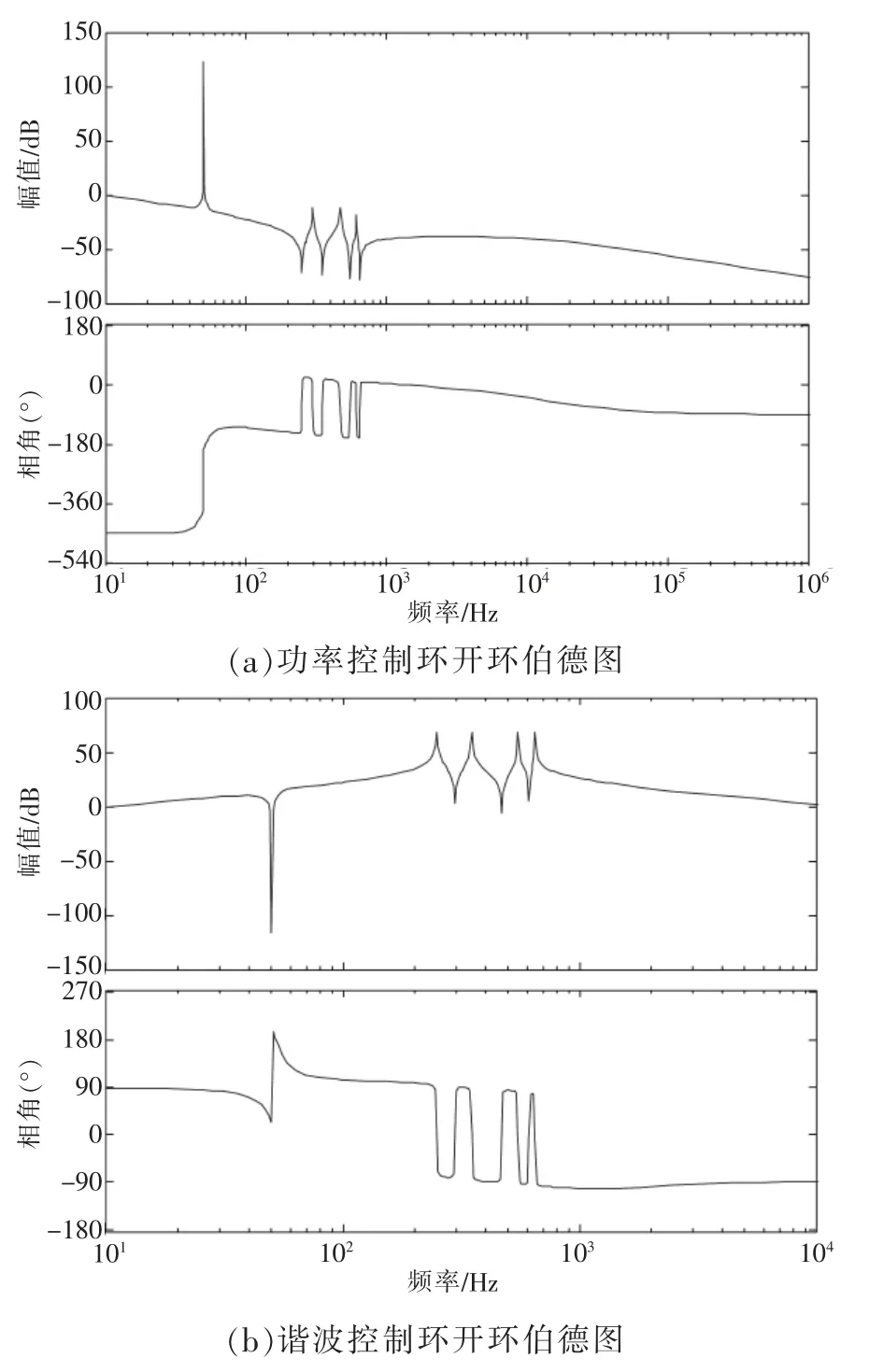
圖8 功率控制環和諧波控制環的開環伯德圖

2.3 傳統PR 控制器的諧波控制環穩定性分析

為了與傳統方法進行對比，諧波抑制控制器傳遞函數GH（s）可采用式（6）傳統PR 控制器進行并聯成組，得到諧波抑制控制器傳遞函數Gh（s）：

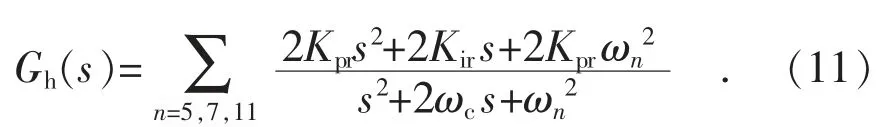
將式（11）代入到式（10）諧波控制環的開環傳遞函數GH2（s）中，得到基于傳統PR 控制器的諧波控制環的開環傳遞函數Gh2（s），采用MATLAB繪制Gh2（s）的伯德圖，如圖9 所示。

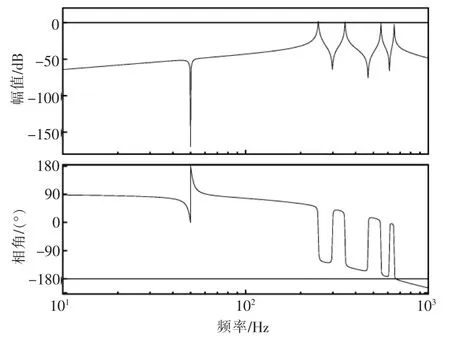
圖9 傳統PR 控制器的諧波控制環開環伯德圖

相頻曲線中，由于控制鏈路延時和被控對象（阻感性負載）自身的相位滯后，增大Kpr，Kir很容易使得相頻曲線在高頻段最先穿-180°線，使得系統不穩定。而采用控制鏈路延時補償的PR 控制器圖8 所示，諧波控制環高頻段相頻曲線依舊滿足穩定性要求。

3 試驗驗證

為了驗證所提網側電流控制方法的正確性，在RTDS 動模實驗平臺搭建了如圖1 所示的三端MMC-MVDC 配電網仿真平臺。三端MMC-MVDC配電網RTDS 仿真平臺是一種半實物的架構，RTDS 仿真系統通過對模型的運算來實現一次系統的功能，其與工程實際使用的控制保護設備的連接如圖10 所示[20-21]。

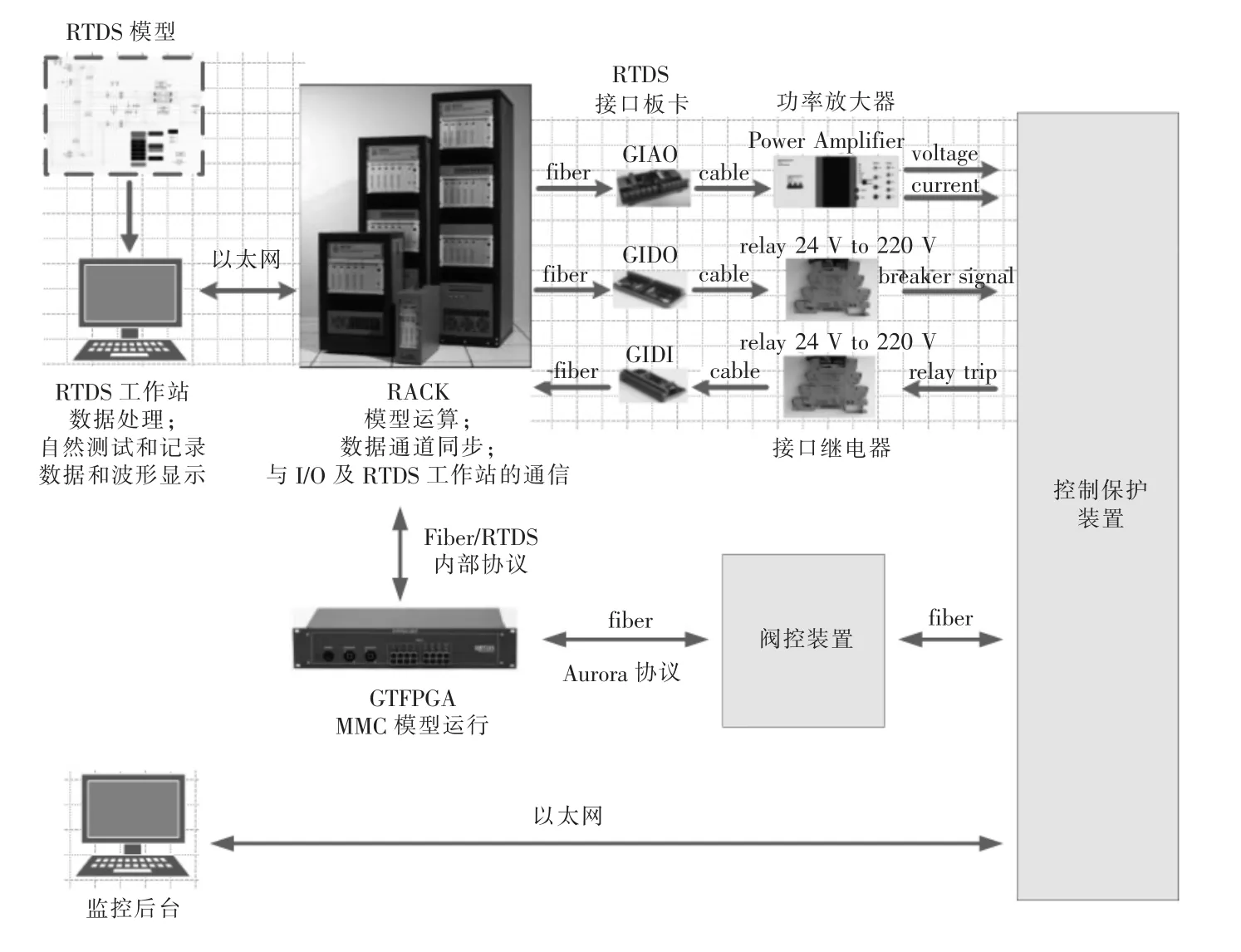
圖10 三端MMC-MVDC RTDS 試驗平臺整體架構

實驗使用的三端MMC-MVDC 柔直工程，相關控制參數如表1 所示。

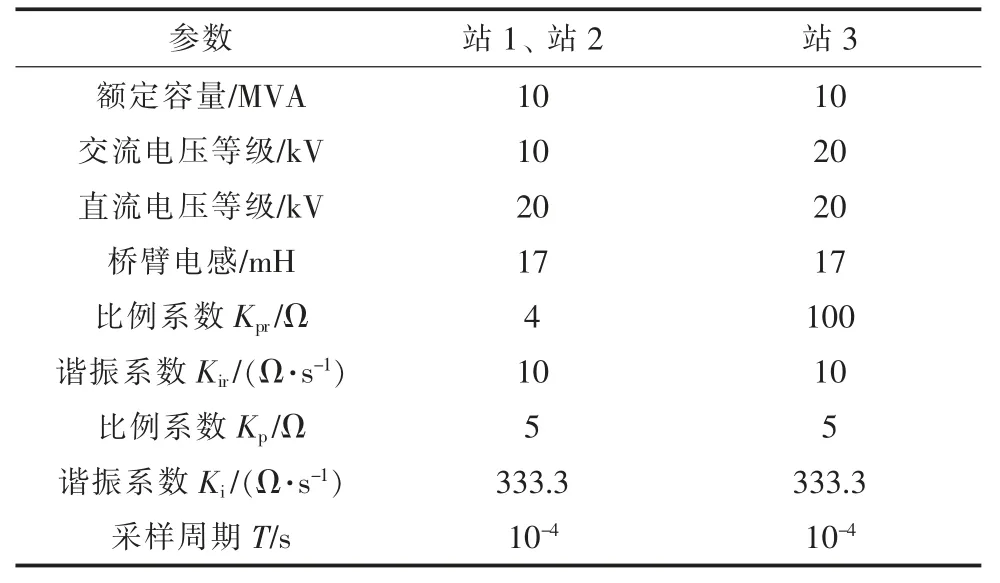
表1 三端MMC-MVDC 試驗參數

試驗中，在站1 進行網側電流諧波抑制試驗。站1 工作于PQ 控制模式，有功功率指令值為2 MW，無功功率指令值為0 Mvar，非線性負載設置為諧波注入形式，5 次、7 次、11 次諧波電流均為12 A。

MMC-MVDC 運行過程中，有功功率、無功功率控制是基礎功能，諧波抑制功能可根據需要投退，本試驗驗證諧波抑制策略投入后，網側諧波電流的治理效果。

3.1 單次諧波抑制試驗

非線性負載分別注入5 次、7 次、11 次諧波電流，0.04 s 時分別投入5 次、7 次、11 次諧波抑制功能，5 次、7 次、11 次單次諧波抑制結果如圖11（a）、（b）、（c）所示，諧波抑制功能投入后，換流器電流ivj補償諧波電流，ivj中諧波電流明顯增加，約一個基波周期內，網側電流isj中的諧波被有效抑制。

3.2 多次諧波同時抑制試驗

非線性負載同時注入5 次、7 次、11 次諧波電流，0.04 s 時同時投入5 次、7 次、11 次諧波抑制功能，5 次、7 次、11 次諧波同時抑制結果如圖12（a）所示，諧波抑制功能投入后，換流器補償電流中諧波電流明顯增加，約在一個基波周期內，網側電流中的諧波被有效抑制。

諧波抑制的數據統計如圖12（b）、表2 所示，20 次諧波范圍內無其他次諧波放大，5 次、7 次、11 次諧波抑制比均超過83%，THD 下降超過84%。

表2 諧波抑制數據統計

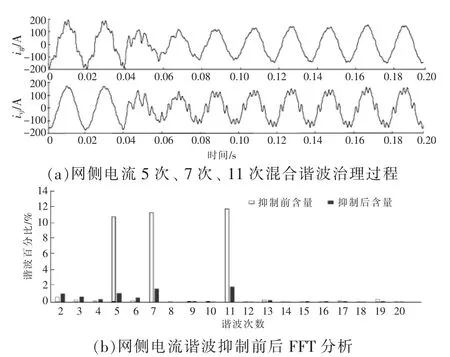
圖12 多次諧波電流同時抑制試驗

4 結論

為實現配電網柔直功率控制兼諧波抑制功能，滿足對非線性負荷應用場景的電能質量治理需求，本文提出了基于諧振控制器的網側諧波電流抑制策略，并補償控制鏈路延時，提升系統在高頻段的穩定性。通過MATLAB 分析了功率控制環和諧波抑制環幅頻特性，并與傳統諧振控制器穩定性對比，驗證了本文所提的控制策略的優越性。最后進行RTDS 單次和多次諧波抑制試驗，試驗結果表明，本文提出的控制策略對5 次、7次、11 次諧波有良好的治理能力。