城市軌道交通控制測量問題解決方案探討
李 禺,陳尚云
(四川中水成勘院測繪工程有限責任公司,四川 成都 610072)
0 前 言
目前部分城市存在交通擁堵現象并且日益嚴重,為了長期有效地解決城市內部出行擁堵問題,各大城市均在進行城市軌道交通建設。而任何一個建設項目均包括規劃設計、施工建設和運行維護三個階段,測量在這三個階段中均是不可缺少的工作,而測量工作的關鍵環節是控制測量。
本文對城市軌道交通控制測量常見問題進行了詳細敘述,并結合實際項目發現的問題給出了相應解決方案。
1 城市軌道交通控制測量的目的和控制測量系統建立方法
1.1 城市軌道交通控制測量的目的
城市軌道交通控制測量的目的是為項目提供平面基準和高程基準[1]。
1.1.1 平面基準
平面基準應包括:
(1)大地基準,如國家采用的現行大地基準為2000國家大地坐標系;
(2)平面坐標系。①標準3°分帶或6°分帶高斯投影平面直角坐標系,投影面大地高為零;②改變投影中央子午線、改變投影面大地高或既改變投影中央子午線又改變投影面大地高的獨立坐標系(即工程獨立坐標系);獨立坐標系應與標準坐標系建立轉換關系。③工程獨立坐標系邊長投影變形不應大于15 km[2]。
1.1.2 高程基準
城市測量應采用統一地高程基準[3]。國家采用的現行基準為1985國家高程基準,高程成果為正常高,也有因保密需要采用與1985國家高程基準正常高有轉換關系的獨立高程系(即工程獨立高程系)。
1.2 城市軌道交通控制測量系統建立方法
由于城市建(構)筑物密集,人口密度大,給控制測量帶來很多的不利,為了最大程度地降低不利因素對控制測量工作的影響,線路平面控制網采用GNSS網建立,高程控制網采用二等水準網建立[4]。
GNSS網具有如下優勢:點位不受通視條件的限制;網形結構無強制要求;可全天候觀測;可多臺套聯合作業提高作業效率和成果精度。
不足之處是誤差來源多,主要體現在:與衛星有關的誤差;與信號傳播有關的誤差;與接收機有關的誤差;相對論效應;圖形強度的影響;其他因素。
二等水準網的優勢在于:點位選擇靈活;觀測時受外界影響小;控制誤差的方法多,成果精度高;復測成果穩定性分析較為簡單。
從GNSS測量的誤差來源可知,GNSS成果受很多因素的影響使得GNSS網復測成果包含多方面的誤差,給穩定性分析帶來較大的難度,本文著重對GNSS網復測常見問題進行分析,并針對這些問題提出相應的解決方案。
2 GNSS網復測常見問題
2.1 GNSS定位原理
GNSS定位系統由地面控制部分(跟蹤站)、空間部分(工作衛星和在軌備用衛星)和用戶設備部分(接收機)組成。GNSS定位原理是通過觀測GNSS衛星和用戶接收機天線之間距離,并根據已知的衛星瞬間坐標按空間后方交會的公式來確定用戶接收機所對應點的三維坐標,如圖1所示。
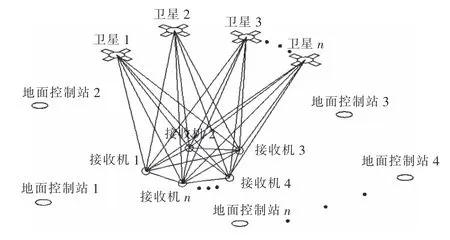
圖1 GNSS定位示意
2.2 GNSS定位中的誤差來源
2.2.1 與衛星有關的誤差
衛星星歷誤差。星歷誤差指的是衛星理論位置與實際位置之差。星歷誤差的大小取決于衛星定規系統的質量和星歷的外推時間間隔。
衛星鐘的鐘誤差。衛星上使用的雖然是高精度的原子鐘,但同樣也存在系統誤差(如鐘差及鐘速、頻漂等偏差)和隨機誤差。
2.2.2 與信號傳播有關的誤差
與信號傳播有關的誤差包括:電離層延遲、對流層延遲、多路徑誤差。
2.2.3 與接收機有關的誤差
與接收機有關的誤差有:接收機的鐘誤差、接收機的位置誤差、接收機的測量噪聲。
2.2.4 圖形強度的影響
由于GNSS定位原理是空間后方交會,因此點位精度與圖形強度密切相關,而圖形強度取決于GNSS衛星的空間分布和GNSS接收機所在的位置。
2.2.5 其他因素
此外還包含一些其他因素,如GNSS控制部分人為或計算機造成的影響;由于GNSS控制部分的問題或用戶在進行數據處理時引入的誤差等;數據處理軟件的算法不完善對定位結果的影響。
經過眾多項目驗證GNSS網復測成果與前期成果比較除偶然誤差外,主要表現在系統誤差,因此后期復測資料采用單點掛靠無約束平差成果間存在一定的平移、縮放和旋轉,為了消除或削弱系統誤差的影響,采用已知系統分析法將復測單點掛靠成果歸算為以前期成果為已知系統的成果。
3 項目成果分析
3.1 某地鐵項目平面控制網約束平差成果
3.1.1 某地鐵項目平面控制網首級網約束平差成果
首級控制網點首期成果與復測固定點約束平差成果見表1。

表1 首級控制網點首期成果與復測固定點約束平差成果分析比較
從表1可知Δx和Δy絕大多數為負,顯然存在系統差。GNSS網首級網點分布情況如圖2所示。
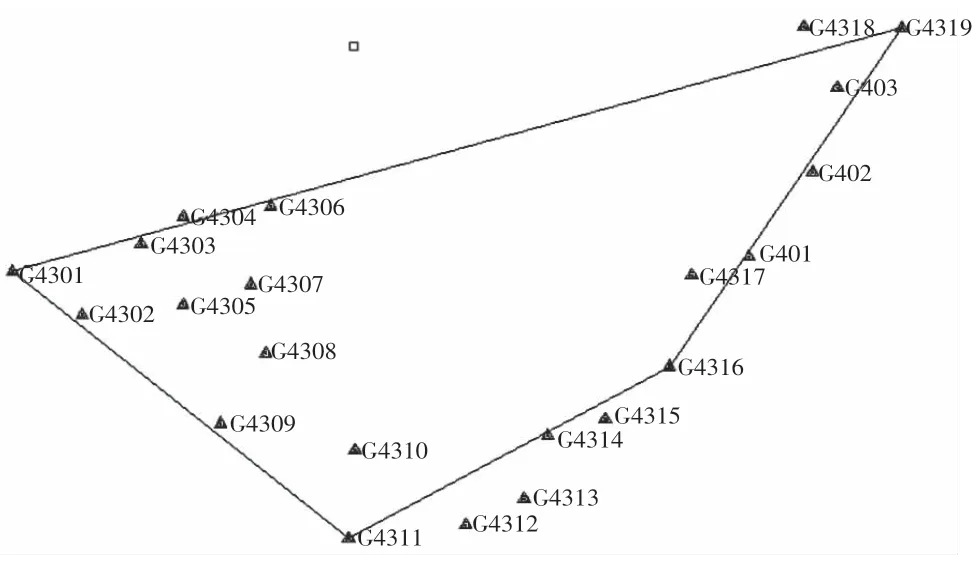
圖2 GNSS首級網點分布
3.1.2 某標段加密網約束平差成果
某標段加密網點首期成果與復測固定點約束平差成果見表2。
從表2可知,復測成果與已知成果間較差全為負值,顯然存在系統誤差。加密網網形見圖3。
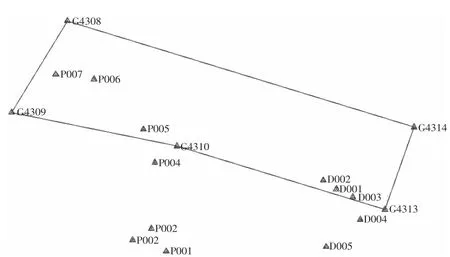
圖3 加密網網形
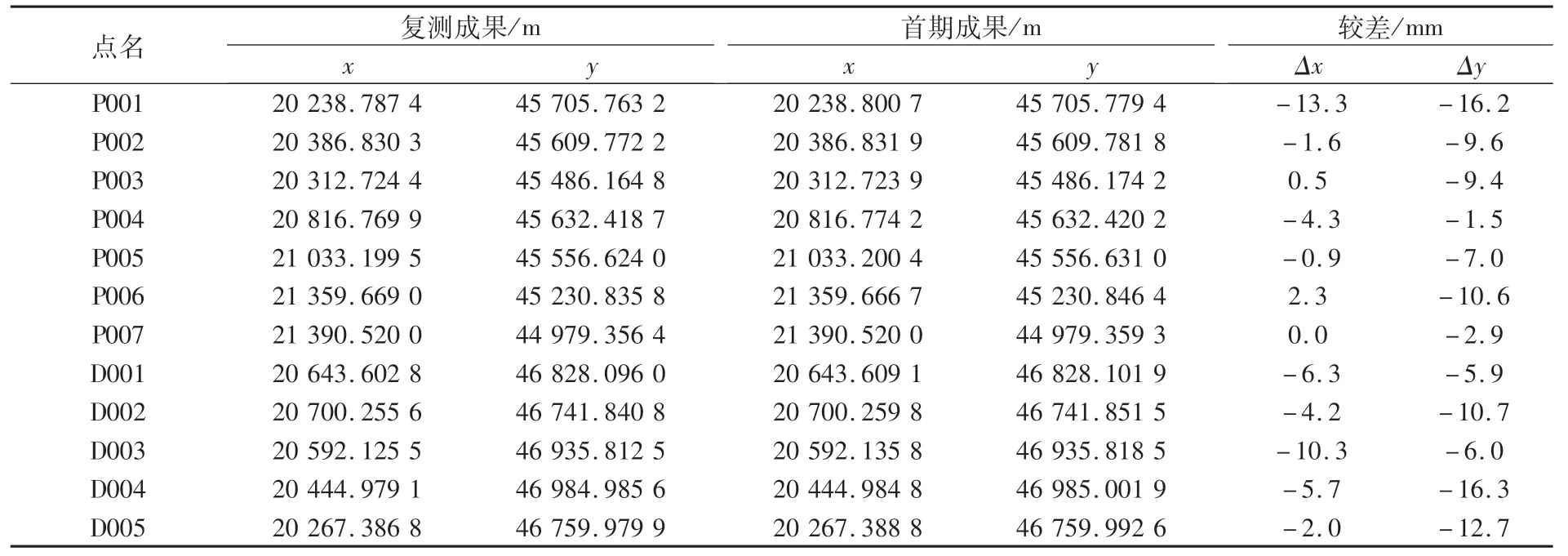
表2 某標段加密網點首期成果與復測固定點約束平差成果分析比較
3.2 某地鐵項目平面控制網無約束平差成果
3.2.1 首級無約束平差成果
首級網復測無約束平差成果和首期成果見表3。
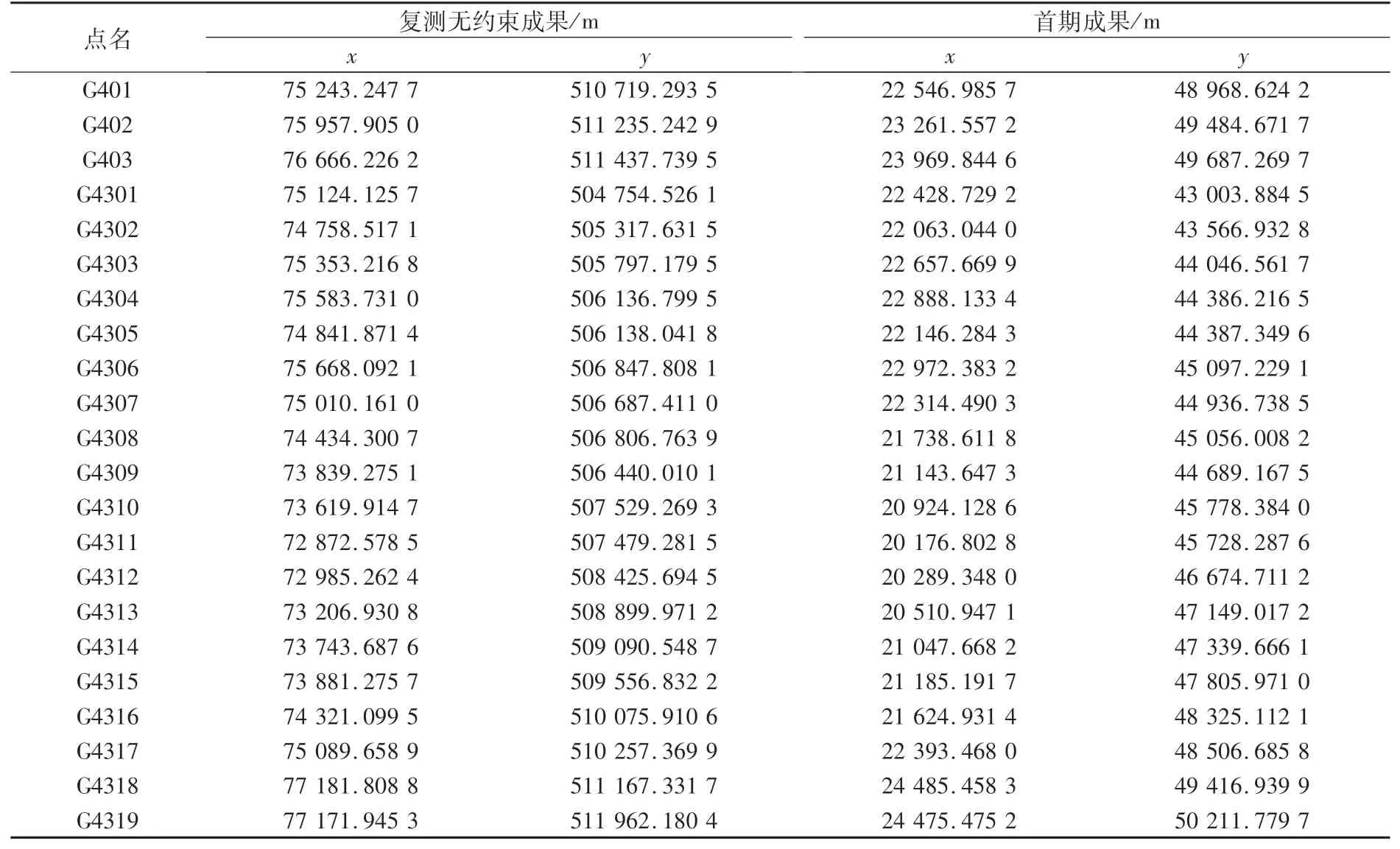
表3 首級網復測無約束平差成果和首期成果
利用表3中的數據采用二維已知系統穩定性分析法計算復測成果的穩定性情況,計算結果見表4~7。
從表4~5可知有19個穩定點計算的已知系統穩定性分析轉換模型縮放系數為0.999 991 809 6,說明實際投影面大地高并非是成果表注明的大地高h,而是h-(1-0.999 991 809 6)×6 369 000。

表4 二維已知系統穩定性分析轉換模型計算
復測無約束平差成果—首期成果已知系統轉換模型:

式中,x、y為復測無約束平差成果;X、Y為復測無約束平差成果—首期成果已知系統轉換成果。

表5 二維已知系統穩定性分析轉換模型特征值計算
從表6可知,復測無約束成果已知系統轉換后與首期成果比較,僅有3個點偏差大于6 mm,最大偏差為10.6 mm,由此可見復測成果與首期成果精度均很高。復測最終成果取穩定點的均值和偏差點的已知系統轉換值見表7。
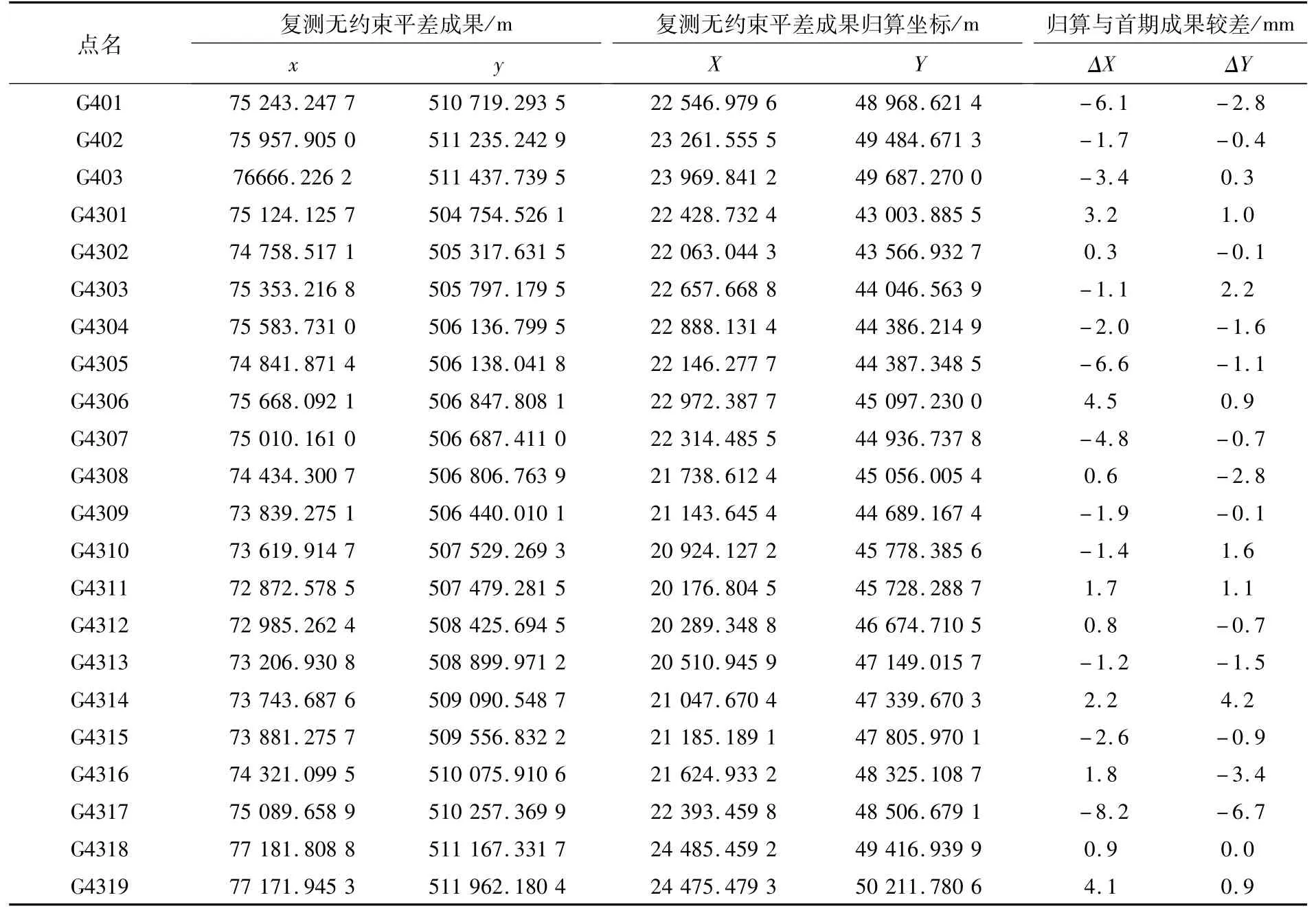
表6 復測無約束平差成果已知系統轉換計算
從表7可知,除3個漂移點外,ΔX有9個負值,極值為-2.4 mm,有10個正值,極值為2.2 mm,ΔY有8個負值,極值為-1.7 mm,有8個正值,極值為2.1 mm;由此可見采用已知系統分析后的最終成果除漂移點外,坐標較差基本符合正態分布,證明已知系統分析法科學合理。
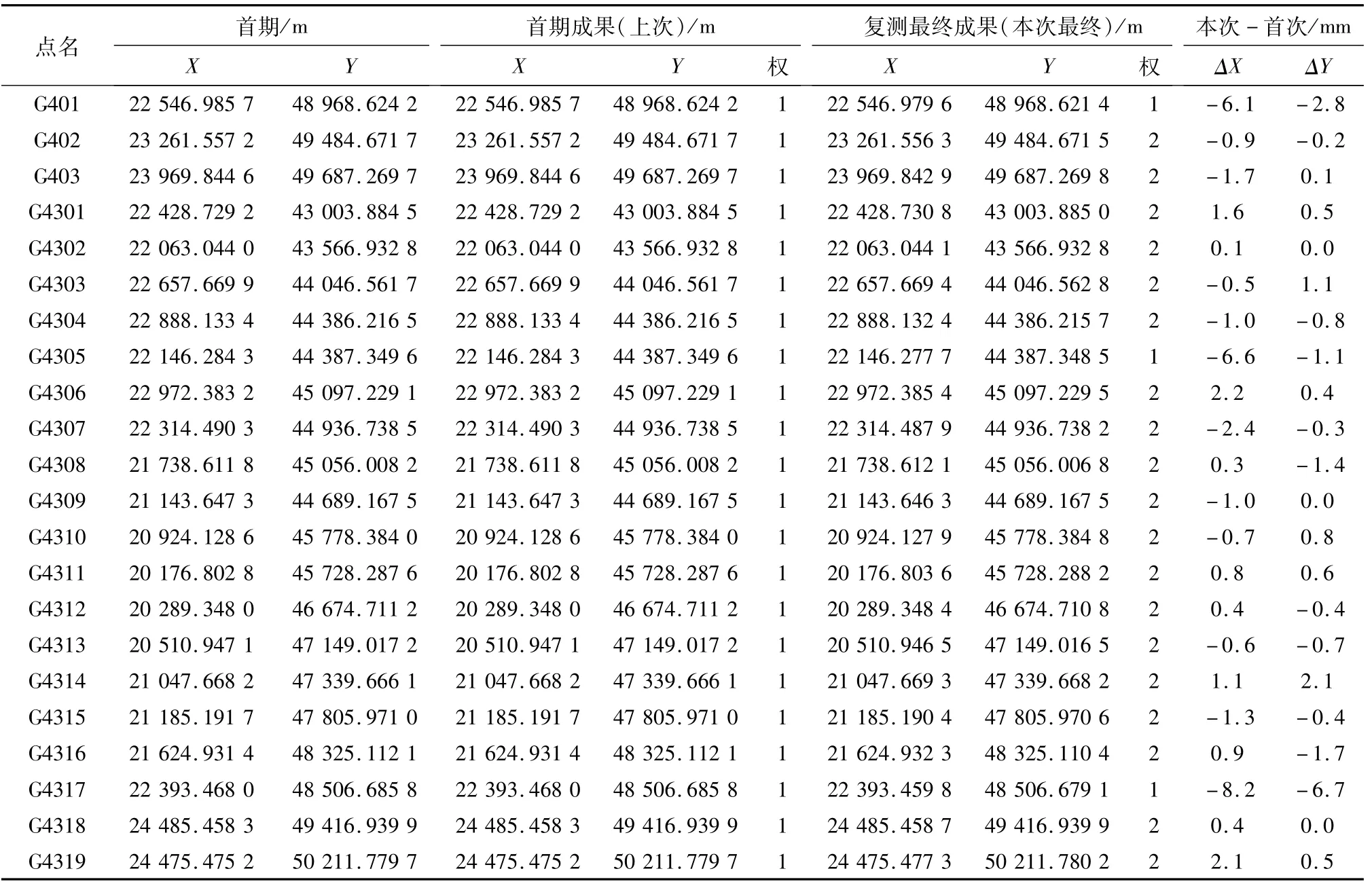
表7 復測最終成果計算
3.2.2 加密網無約束平差成果
加密網復測無約束平差成果和首期成果如表8所示。
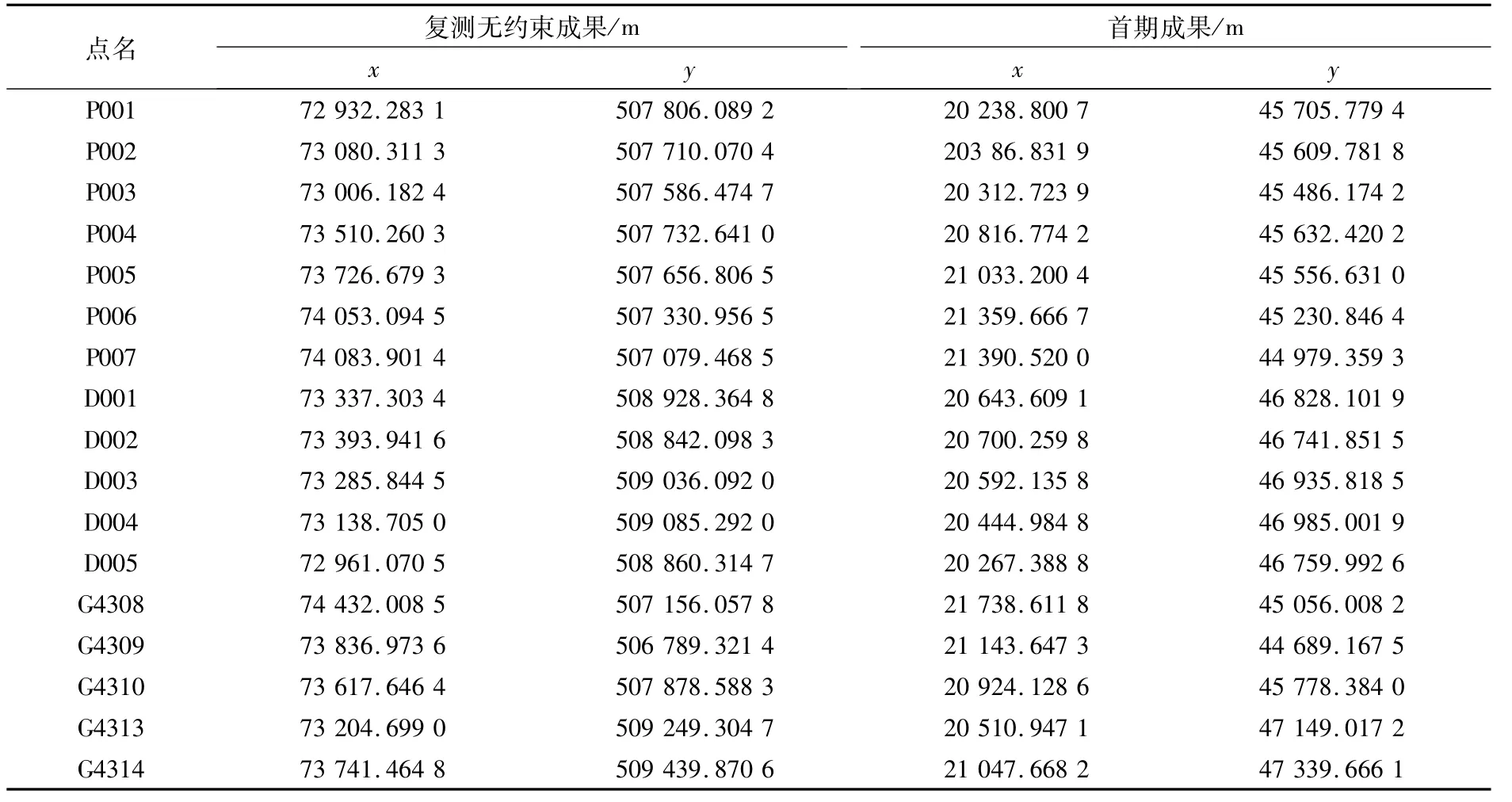
表8 加密網復測無約束平差成果和首期成果
利用表8中的數據采用二維已知系統穩定性分析法計算復測成果的穩定性情況,計算結果見表9~12。
從表9~10可知13個穩定點計算的已知系統穩定性分析轉換模型縮放系數為0.999 990 367 1,說明實際投影面大地高并非是成果表注明的大地高h,而是h-(1-0.999 990 367 1)×6 369 000。

表9 二維已知系統穩定性分析轉換模型計算
復測無約束平差成果—首期成果已知系統轉換模型:

式中,x、y為復測無約束平差成果;X、Y為復測無約束平差成果—首期成果已知系統轉換成果(見表11)。

表11 復測無約束平差成果已知系統轉換計算

表10 二維已知系統穩定性分析轉換模型特征值計算
從表12可知,除4個漂移點外,ΔX有6個負值,極值為-1.4 mm,有6個正值,極值為1.2 mm,ΔY有7個負值,極值為-2.3 mm,有5個正值,極值為2.3 mm;由此可見采用已知系統分析后的最終成果除漂移點外,坐標較差基本符合正態分布,證明已知系統分析法正確性。
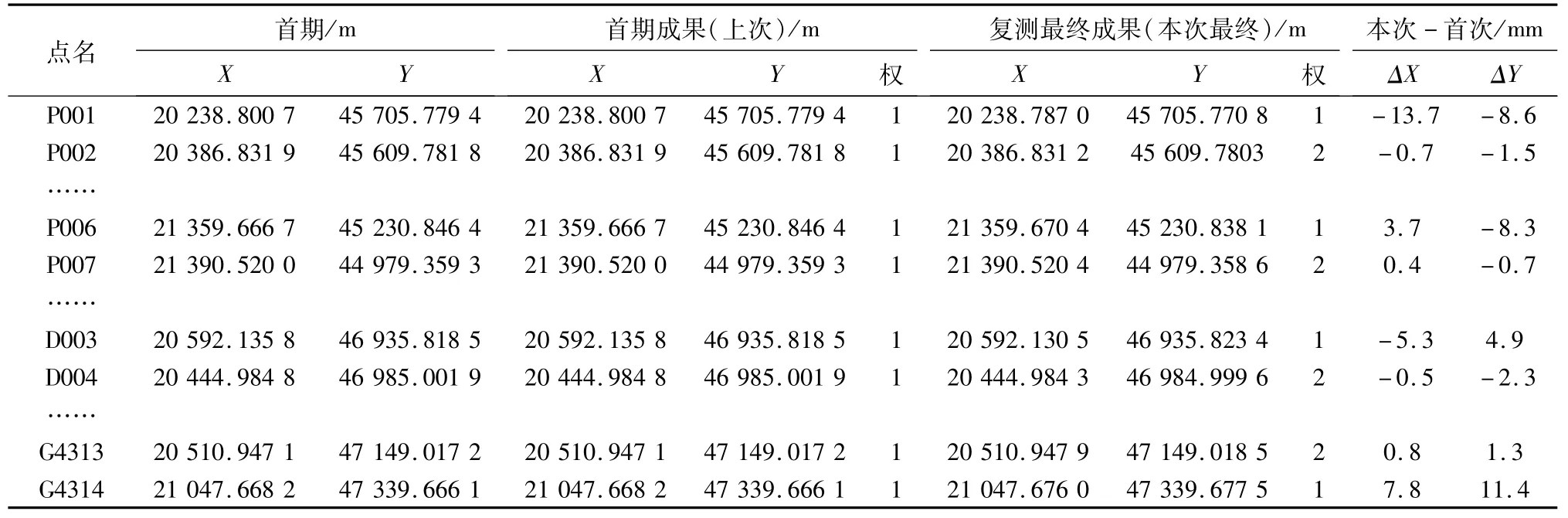
表12 復測最終成果計算
3.2.3 約束平差成果與無約束成果已知系統歸算成果差異原因分析
從無約束平差成果與首期成果已知系統分析可知,GNSS復測存在點位漂移,如同期復測資料中首級網復測G4314為穩定點,但加密網復測G4314為漂移點,因首級網和加密網為同期復測,點位不可能發生位移,故強制采用固定點約束平差,必將把含有漂移的成果差異傳遞到其他點上,使得復測固定點平差成果含有系統差。
4 結 論
由于城市建(構)筑物密度大,通常城市地鐵控制采用GNSS測量法建立首級平面控制網和加密平面控制網,但GNSS測量受諸多因素影響,復測采用固定點平差的成果與前期成果間通常存在系統誤差,本文提出的已知系統分析法既能剔除漂移點,又能使處理后的成果符合正態分布,由此證明本文提出方法的正確性。
對復測成果異常的點,若相鄰點反算的邊長相對中誤差大于《城市軌道交通工程測量規范》(GB/T 50308—2017)表3.2.1的規定,則應采用高精度全站儀測邊比較確定最終采用前期成果,還是本期復測最終成果。

