高考課標卷概率統計試題的特點及其教學啟示——基于2011—2020年全國課標卷的分析

李亞瓊，徐文彬

高考課標卷概率統計試題的特點及其教學啟示——基于2011—2020年全國課標卷的分析

李亞瓊1，2，徐文彬1

（1．南京師范大學 課程與教學研究所，江蘇 南京 210079；2．南京藝術學院附屬中等藝術學校，江蘇 南京 210013）

基于2011—2020年52套全國課標卷，從考查總分、考查知識、試題特點和命題導向4個方面對課標卷中概率統計試題特點進行了統計與分析．概率統計試題在全國卷中考查總分占比呈增加趨勢．具體而言，側重用數據呈現的規律解釋隨機現象，用概率或統計模型表達隨機現象的統計規律；情境的創新融入了綜合化的新趨勢；重視概率與函數、概率與不等式、概率與數列等交匯知識在試題中的融合考查；呈現出重視數學文化滲透、問題情境載入和知識融合創新的命題導向．基于高考對教學的導向作用，概率統計專題教學應重視：研究新課標，關注新舊過渡；回歸教材，重視知識的整體結構性；基于學情，加強學生“四能”培養；落實教學，嘗試“整—分—聯”教學思路．

高考課標卷；概率統計；試題特點；整體教學；“整—分—聯”教學思路

概率統計是研究隨機現象數量規律的數學學科，包括通過有效地收集、整理和分析相關數據，從而對所考查的問題做出推斷和預測[1]．陳希孺在《概率論與數理統計》中提到：從實用的角度來看，概率的統計定義是一種通過實驗去估計事件概率的方法，而統計是研究怎樣收集數據，并對數據進行分析，進而對研究的問題進行推斷的方法．概率統計知識是高中數學學習的重要內容之一，2000年高考試卷中首次出現概率試題，2001年高考試卷中出現統計試題，2004年高中教材中大量增加概率統計內容，考查題型、考查方式等有了較大的變化[1]．《普通高中數學課程標準（2017年版）》（以下簡稱新課標）中提到：概率的研究對象是隨機現象，引導人們從不確定性的角度認識客觀世界，同時提供重要的思維模式和解決問題的方法．統計的對象是數據，核心是數據分析，概率為統計的發展提供理論基礎[2]．總之，對概率統計的考查已由摸索、穩定進入到創新的階段．

1 問題提出

傳統概率統計教學中，往往重視概率統計的科學工具性價值，而忽視其文化內涵與育人功能[3]．2014年啟動的新高考方案，提出了文理不分科的新要求．高中文理科學生的較大差異體現在空間想象能力和數據處理能力，與之相應的知識內容是立體幾何和概率統計[4]．新課標將“數據分析”作為高中數學課程目標中培養學生所必備的數學素養之一，這既凸顯高中課程中概率統計內容的教育價值，也是對概率統計的育人價值提出更高的要求．高考實行不分文理科的改革后，數學科考試中概率統計的定位、考查內容和形式以及考生群體和水平都會隨之發生變化，所以需要研究概率統計試題、試卷結構和難度要求等[5]，結合試題研究回歸課標目標要求、落實課標教學目標、開展有效教學[6]，發揮新高考數學科對中學數學教學的積極導向作用，以期促進學生實現自我發展．

新高考數學科概率統計試題有哪些特點？新課標在概率統計的考查要求上作了哪些變化？新高考概率統計的導向教學作用可能體現在哪里？研究者結合2011—2020年全國卷（其中包含2020年新高考卷），匯總了這10年的全國Ⅰ、Ⅱ、Ⅲ文理卷和2020年的新高考Ⅰ、Ⅱ卷共52套試卷（其中2011—2015年共20套、2016—2019年共24套及2020年共8套），并對比了不同時期全國卷概率統計考查的題型和分值，研讀新課標中對概率統計的要求．基于高考導向教學，引起教學上的重視，加大概率統計在教育教學中的貢獻[3]．

2 概率統計試題的特點

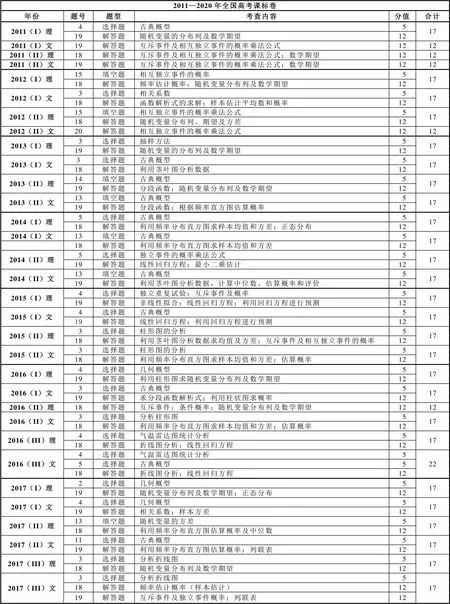
結合近10年全國課標卷，梳理出高考概率統計部分的考查知識及對應分值（具體可參見附錄），需要說明的是，因計數原理、排列組合及二項式定理較概率統計知識具有相對獨立性，故這3部分不在附表統計范圍之內，以下分析中不再說明．

2.1 總體特點

從歷年試題統計可以看出：試題在考查概率與統計知識的同時，更側重于問題情境的嵌入以及思想方法的滲透．

（1）從考查總分來看：該專題考查總分17分的出現37次，總分22分的出現9次，總分12分的出現6次，試題的題量、題型、分值均有適度的變化，總體趨勢是選填題考查1題左右和解答題考查1題，以中檔題或中檔偏易題為主，考查總分約占全卷總分的12%左右．

對選填題的知識統計（如表1所示）表明，52套試卷中共考查了56道選填題，其中有22次考查古典或幾何概型；統計圖分析（如頻率分布直方圖、餅形圖、柱形圖、折線圖、莖葉圖、氣溫雷達圖等）、抽樣及樣本估計、互斥事件及獨立事件概率共考查29次；隨機變量分布列及其數字特征、回歸方程或相關系數共考查5次．由此可以看出，文理卷在選填題上均側重考查古典概型、抽樣及樣本估計、統計圖分析及互斥或獨立事件概率．

表1 2011—2020年全國課標卷概率統計（選填題） 知識考查次數分布

表2 2011—2020年全國課標卷概率統計（解答題） 知識考查次數分布

注：由于解答題考查的綜合性，表中對相關知識進行了融合統計，共統計4個知識的考查情況．其中將“互斥或獨立事件概率”并入“隨機變量”進行統計；因為統計圖分析的工具性作用及知識交叉考查特點，以主要考查知識來統計次數，比如“統計圖分析”與“回歸分析”結合考查時，記入“回歸分析”；“統計圖分析”與“樣本估計”結合考查時，記入“抽樣及樣本估計”．

2.2 試題特點

結合近10年52套全國卷的研究，對高考概率統計的考查進行了總體分析，基于此，將繼續進行試題考查特點的分析．

2.2.1 重視基礎知識的變式考查

2.2.2 重視問題情境的創新考查

新課標在劃分學業質量水平時，首先考慮了“情境與問題”，可見高考對數學素養的考查需要在一定情境中進行[7]．而通過對近10年全國課標卷概率統計試題的研究發現：試題重視情境的創設和問題的提出，這與新課標的要求相契合，也是以后研究需要繼續關注的．

所分析的52套試卷中，共計考查109道概率統計題（同一年文理卷出現題目相同均重復計算）．依據新課標對情境進行劃分：現實情境、數學情境和科學情境[2]．由表3知：現實情境考查了94次，占比達86.2%；數學情境考查了11次；科學情境考查了4次．由此可以看出解答題及客觀題以現實為情境較多，主要考查考生的分析問題、解決問題的能力（以例1—例3來舉例說明）．

表3 2011—2020年概率統計試題的“情境”分布

例1 （2012年全國Ⅰ卷·理15）

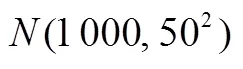
例2 （2018年全國Ⅱ卷·理8）

例3 （2020年全國Ⅰ卷·理5）

以上3個例子中，例1是以科學情境融入考查正態分布，例2是以數學情境為背景考查古典概型，例3考查現實情境背景下的回歸分析，這3個例子均考查學生對新情境的學習能力、結合新情境及相關統計知識解決問題的能力．

2.2.3 重視數學建模能力的考查

歷年課標卷概率統計考查學生能根據實際問題正確建立概率模型，并能在實際問題中加以解釋，將數學解答轉化成對現實對象的分析．當然對概率的考查不應只停留在概率計算的層面，其出發點和歸宿都是解決問題，即能夠利用計算結果為決策提出關鍵性的依據．而對統計的考查側重于用樣本數字特征對總體進行估計，考查樣本估計總體的統計思想[8]．

近10年全國卷中，概率統計試題多以現實情境為背景，這就要求學生能夠從數學的視角去發現問題、提出問題、分析問題、構建模型、計算結果及依據結果提出決策．全國卷重視對學生數學建模能力的考查，而概率統計的知識與現實生活和科技發展緊密相關，具有較強的理論性和應用性，是數學模型的重要載體[1]．

2.3 命題導向分析

以全國課標卷概率統計試題的統計數據為基礎，結合統計圖分析及試題特點[9]，將繼續探討命題導向啟示，具體分析如下．

2.3.1 知識融合創新

結合表4和圖1可以看出，概率統計考查總分占比呈增加趨勢．隨著文理不分科的實行，概率統計命題有了綜合化的趨勢，重視概率與函數、概率與不等式、概率與數列等交匯知識在試題中的融合考查．知識點考查上，加大了學科間知識融合命題，注重隨機思想、抽樣思想、或然與必然思想[10]；注重與情境的結合，突出概率統計在解決實際問題中的作用．素養考查上，側重理解抽樣方法的統計意義，側重考查用數據呈現的規律來解釋隨機現象，側重用概率或統計模型來表達隨機現象的統計規律．

2.3.2 數學文化滲透

高考概率統計試題重視考查數據分析和統計素養的同時，也重視數學文化的育人價值．數學學習的主要目的是引導學生形成邏輯思維能力和形象思維能力，形象思維是先導，邏輯思維是核心．試題通過滲透數學文化背景，如音樂中的數學、體育中的數學、數學史料等，重視形象思維和邏輯思維的有機融合，在形象思維的基礎上增強學生的理性思維能力，培養學生從感性走向理性，從而走向以文化人的目標．

表4 2011—2020年概率統計試題的考查總分均值分布

圖1 2011—2020年考查分值均值變化趨勢

2.3.3 問題情境載入

情境是高考實現價值引領、素養導向、能力為重、知識為基的綜合考查載體，高考試題以知識為基礎，情境為載體，從而可以實現考查目的與形式的統一[11]．概率統計試題中情境載入目的是：引導學生能進行模型識別、現象解釋并據此提供決策；能夠在熟悉的數學情境中，選擇合適的抽樣方法去收集數據，選擇合適的概率模型去分析數據等；能夠在關聯的現實情境中，選擇合適的隨機變量刻畫隨機現象，理解抽樣方法的統計意義，運用適當的概率或統計模型表達隨機現象的統計規律；能夠在綜合的情境中，結合數據規律，理解統計意義并做出合適的統計決策．當然，為保證試題情境能夠發揮準確價值，情境創設時需要遵循真實性、簡潔性、公平性和一致性[12]．

3 結合試題分析 啟示教學實踐

如何將知識融合創新、數學文化滲透及問題情境載入有機結合并能運用于教學？結合新舊課標的變化比較，提出新課標下的概率統計的教學啟示．

3.1 研究課標 關注新舊過渡

3.2 回歸教材 重視知識的整體結構性

概率統計試題重視基礎概念，預示教學要回歸教材．教材中，關于概率統計專題的知識點較為分散，前后知識交叉排列．新課標重視數學科知識體系結構化，這就需要教師結合課標回歸教材，關注概率統計的整體性，系統地進行單元整體教學[13]．當然，整體性需要教師關注知識的層次性，教材知識邏輯與學科知識邏輯的關聯性，及教師對主題知識的整體結構把握[14]，即概率統計知識整體性體現為層次性、關聯性和結構化．于是研究中結合對新課標的解讀，將教材中概率統計的內容進行了結構化梳理（如圖2所示）．需要說明，從知識的整體性考慮，結構圖中包含了計數原理和二項式定理的內容．

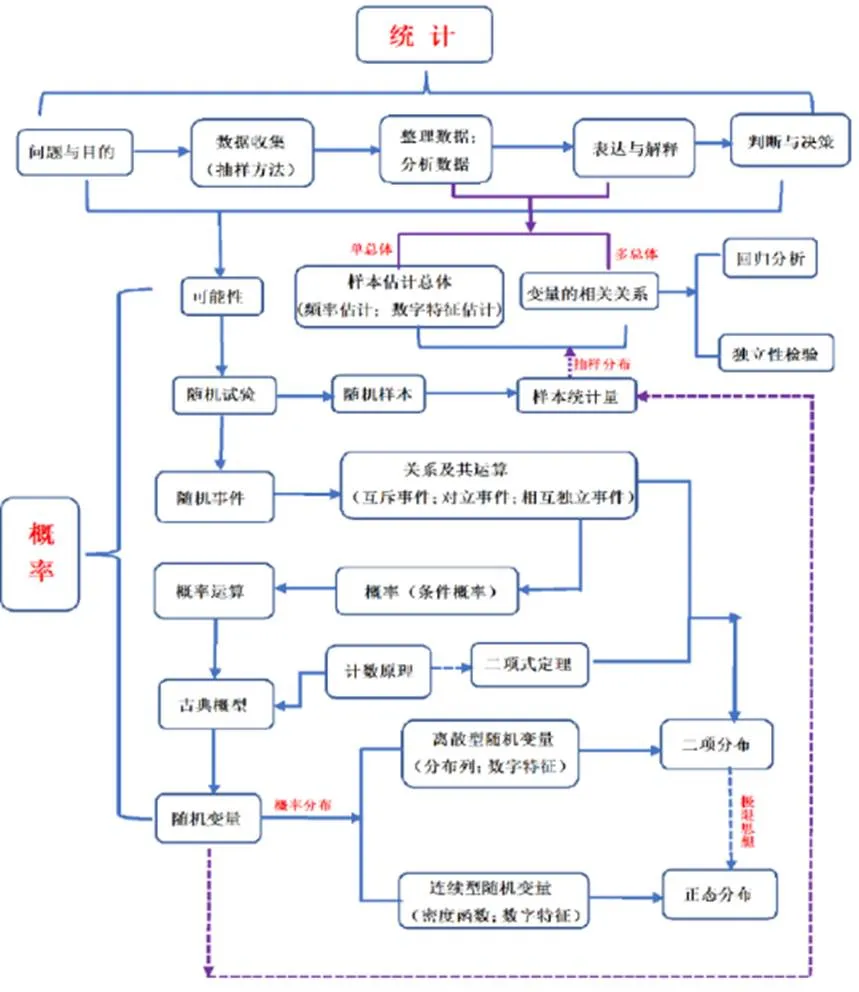
圖2 2017版課標中概率統計內容的整體結構

3.2.1 知識的層次性

圖2縱向關注了概率統計知識的結構層次及知識融合，橫向關注了必修內容和選擇性必修內容的銜接，體現知識的螺旋式上升．比如統計的目的是服務于概率，這個結構圖能較好地呈現統計知識與概率知識的內在關系．由隨機試驗、隨機事件、事件的關系自然呈現接下來的知識點——概率運算、隨機變量等，體現知識的動態生成性與層次性．

3.2.2 知識的關聯性

從圖2可以看出，“整理、分析數據”和“表達與解釋”共同為研究“樣本估計”和“相關關系”作鋪墊．另外，隨機變量的本質是樣本統計量，而利用樣本統計量又可以進行樣本估計和相關系數的研究，這樣可以明確知識間的關聯性，使得知識系統更加清晰．比如，由隨機事件及古典概型到計數原理再到隨機變量，這3塊知識如何融合過渡？需要教師去思考．再比如必修教材中，在相關系數部分涉及線性回歸分析，在選擇性必修時會繼續涉及更一般的回歸分析以及獨立性檢驗，所以教師需要關注到知識的關聯性和層次性去組織教學．

3.2.3 知識的結構化

了解知識整體結構圖（如圖2所示）是教師進行整體教學的前提，需要教師對知識進行整體把握，理解知識體系中直觀和嚴謹的關系[15]，厘清知識間的聯系以及同一部分內容中知識的關聯性和層次性，最后呈現出結構化知識體系，再用于教學實踐．因此，回歸教材預示教師首先要回歸教材中的知識內容，消化理解內容蘊含的層次性、關聯性和結構化．教師只有站在這樣的整體視角，才能更好地實施從教到學，在教學中才能關注到概率統計內容的人文價值滲透．

3.3 基于學情 加強學生“四能”培養

高考的導向作用啟示教師在進行整體教學的同時，也要關注學生的“四能”培養[16]．教師在教學中需要關注：

（1）關注學生審題能力，提升學生的數學抽象與直觀想象的數學素養，培養學生發現問題和提出問題的能力；（2）滲透培養數學建模能力，引導學生根據實際問題構建概率模型，分析數據，提升學生數據分析和數學建模能力，培養學生分析問題解決問題的能力；（3）重視數據計算，規范學生的解題習慣和思維訓練，提升學生的邏輯推理和數學運算能力，培養學生解決問題的能力．解題中應體現數學模型化、綜合應用性，強調從知識能力立意轉向統計素養立意．統計素養是學生在掌握知識能力的基礎上，經過反復實踐與反思而后逐漸深化形成[17]，于是在教學中需要滲透思維訓練，培養學生統計學習興趣和提升其統計素養．

3.4 落實教學 嘗試“整—分—聯”教學思路

概率統計知識的整體教學需要教師從章節或單元的角度對教學內容重構，根據章節中不同知識點的教學要求及學生的特點，轉化為符合學生實際的教學結構安排．教學安排上，需要關注學習內容與學習方式是否適應學生的能力要求[14]．結合歷年試題的分析及課標中內容的變化，探討整體視角下對概率統計內容的教學思路，具體包括3個方面．

（1）突出層次，整合教學內容．教師在進行整體教學前，需要進行如圖2的知識梳理．然后教師在教學中才能關注到知識的生長性、必修和選擇性必修中相應知識的聯結性．

（2）突出重點，分解教學內容．教師在進行專題教學中，需要做好知識的再現與深化，教學中需要滲透思想方法、需要關注確定性思維和統計思維的差異、歸納推斷與演繹證明的區別，理解統計推斷結果的或然性．比如，條件概率是含參變量的集合函數，是概率的推廣[18]．教師在教授條件概率時，需要從概念的本質出發，解釋條件概率的理論價值，激發學生學習條件概率的興趣，從而更好地指導教學．（3）設計活動，聯結教學內容．概率統計試題在重基礎的同時，題型靈活、知識交匯、不斷滲透應用與創新，所以教師應該設計典型案例開展教學活動，在案例教學中提煉出時代特色的應用情境，引導學生關注經濟、科技、人文等方面的信息．

綜上所述，在教學中關注“數學文化滲透、問題情境載入及知識融合創新”的有機結合，需要教師：基于學情，以加強學生“四能”培養為目標追求，以課標、教材、知識的整體結構性為關鍵，從而達到“整—分—聯”教學思路，這樣才是高考數學科對教學的正確導向．

4 小結

高考評價體系是包括“核心價值、學科素養、關鍵能力、必備知識”在內的高考考查內容體系，是實現“招—考—教—學”各個環節無縫銜接、良性互動的關鍵，也是發揮高考正向積極導向作用的基礎[19]．基于高考評價體系的意義和原則，對全國課標卷的研究可以起到較好的教學啟示．所以，高中概率統計教學需要關注新舊課標中相應內容的變化，比如，新課標中強調，概率統計內容應關注運用數據分析解決實際問題，重視統計思維和確定性思維的差異，關注理解統計結果解釋實際問題等．當然，教學更需要回歸教材重視概率統計知識的整體結構性，需要基于學情落實“整—分—聯”教學思路，從而提升學生統計素養．總之，教師需要結合課標變化和歷年課標卷概率統計試題的特點，在教學內容上做出整體規劃，做好新舊平穩過渡．

[1] 趙軒，任子朝．高考概率統計試題考查目標的沿革與實現[J]．數學通報，2019，58（10）：39–43．

[2] 中華人民共和國教育部．普通高中數學課程標準（2017年版）[M]．北京：人民教育出版社，2018：30–31，70，75．

[3] 藺云．哲學與文化視角下概率統計課的育人功能[J]．數學教育學報，2002，11（2）：24–26，102．

[4] 張遠增．高考數學不分文理科的探索[J]．中國考試，2019（5）：6–15．

[5] 任子朝，陳昂，黃熙彤，等．高考數學新題型試卷質量分析研究[J]．數學教育學報，2019，28（1）：1–7，48．

[6] 張定強，裴陽．新高考改革背景下數學試卷與課標一致性研究[J]．數學教育學報，2019，28（4）：55–60．

[7] 胡鳳娟．“概率與統計”在高考中的定位與考查研究[J]．基礎教育課程，2019（15）：14–21．

[8] 周遠方，余錦銀．2014年高考“概率與統計、計數原理”專題分析[J]．中國數學教育，2014（7–8）：106–119，127．

[9] 任子朝，趙軒，關丹丹，等．圖形分析法在高考試題評價中的應用研究[J]．數學教育學報，2021，30（1）：37–41．

[10] 王雅琪．談高考中概率與統計的考查[J]．數學通報，2016，55（4）：42–46．

[11] 覃創，嚴忠權，李敏．落實素養為本的高考測評研究——以2020年全國Ⅰ卷數學為例[J]．數學教育學報，2020，29（6）：21–24．

[12] 常毓喜．中學數學教學如何應對高考考試內容的變化以及核心素養的提出[J]．中國考試，2017（2）：52–58．

[13] 浦敘德，顏延亮．例談單元整體教學中的“首呼、中聯、尾應”[J]．中學數學教學參考，2018（5）：50–52．

[14]徐文彬，彭亮，任利平，等．小學數學教材中“認識三角形和四邊形”的內容編排分析與比較——以“人教版”“蘇教版”“北師版”為例[J]．數學教育學報，2021，30（2）：1–7．

[15] 楊怡，梁會芳，張定強．“數學探究”研究二十年：回顧經驗展望[J]．數學教育學報，2020，29（6）：40–45．

[16] 徐穎．“分”“合”“聯”，整體設計三角形單元教學[J]．中國數學教育，2019（12）：17–20．

[17] 嚴卿，喻平．初中生邏輯推理能力的現狀調查[J]．數學教育學報，2021，30（1）：49–53，78．

[18] 李杰民，廖運章．條件概率的本質及其教學建議[J]．數學教育學報，2021，30（1）：54–60．

[19] 教育部考試中心．中國高考評價體系[M]．北京：人民教育出版社，2019：3．

An Analysis of Items Related to Probability and Statistics in College Entrance Examinations from 2011—2020

LI Ya-qiong1, 2, XU Wen-bin1

(1. Curriculum and Teaching Institute, Nanjing Normal University, Jiangsu Nanjing 210079, China;2. Secondary Art School Affiliated to Nanjing University of Arts, Jiangsu Nanjing 210013, China)

Based on 52 sets of national course standard papers from 2011 to 2020, statistics and analysis of the characteristics of the probability and statistics test questions in the papers was carried out along four aspects: the total score of the test, the knowledge assessed on the test, the characteristics of the test questions, and the proposition orientation. The proportion of probability and statistics tests in the national papers is increasing. Specifically, the emphasis is on using the laws presented by data to explain random phenomena, and probability or statistical models are used to express the statistical laws of random phenomena; the integration of situational innovation has a new trend of integration; emphasis on probability and function integrate examination of the intersection of knowledge, probability and inequality, probability and sequence of numbers, etc.; present a proposition orientation that emphasizes the penetration of mathematics culture, the loading of problem situations, and the innovation of knowledge integration. Based on the guiding role of the college entrance examination for teaching, the teaching of probability and statistics should pay attention to the following: studying the new curriculum standards and transitioning between the new and the old; returning to the textbook and emphasizing the holistic structure of knowledge; based on the academic conditions, strengthening the training of students’ “four abilities”; implementing teaching and trying the teaching ideas of “integral-sub- union.”

college entrance examination papers; probability statistics; characteristics of test questions; holistic teaching; teaching ideas of “integral-sub-union”

附錄：2011—2020年全國卷概率統計試題統計匯總