直墻半圓拱巷道圍巖應力分布解析

龐大偉

（潘二煤礦掘進一區103 隊，安徽 淮南 232001）

直墻半圓拱巷道以其受力均勻和穩定性好的優點在煤礦回采巷道中有著廣泛應用。樊曉飛[1]優化了大斷面直墻半圓拱巷道錨桿支護參數；劉朝偉[2]研究了厚煤層直墻半圓拱巷道圍巖破壞特征；何治良等[3]研究了側壓系數不同時直墻半圓拱巷道底腳受力特點；單仁亮等[4]對大斷面直墻半圓拱巷道支護參數進行了優化；陸莉娜等[5]優化了直墻半圓拱巷道襯砌結構；單仁亮等[6]對直墻半圓拱巷道進行了爆破震動數值分析。本文采用復變函數法求解了直墻半圓拱巷道圍巖的應力分布，并分析了直墻半圓拱巷道主應力分布規律。

1 直墻半圓拱巷道圍巖應力分布求解

直墻半圓拱巷道圍巖的自重應力與巷道的原巖應力相比很小，可以忽略不計。直墻半圓拱巷道的原巖應力包括垂直應力σV、水平應力σH和剪應力τ。直墻半圓拱巷道的受力如圖1。

圖1 直墻半圓拱巷道受力示意圖

直墻半圓拱巷道圍巖應力求解問題屬于平面應變問題，可采用復變函數法求解[7]。圍巖應力可由2 個復位勢函數φ（z）和Ψ（z）表示：

式（1）中：ξ=ρ·eiθ為復變量；函數φ0（ξ）和Ψ0（ξ）表示解析函數，可依據文獻[7]求解；函數ω（ξ）表示巷道外域到單位圓內的共形映射函數，可依據文獻[8]進行求解；其他參數、和α取值為：

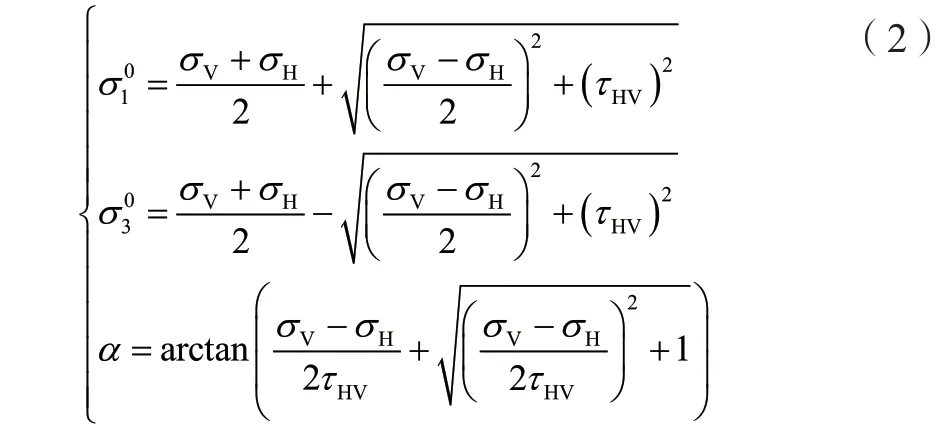
依據求解得到的復位勢函數φ（z）和Ψ（z）可求得巷道圍巖的應力分布為：

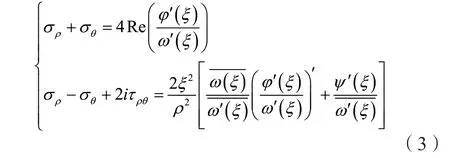
由式（3）求得的應力分布是基于共形映射函數ω（ξ）確定的正交曲線坐標系，可直接按下式計算其主應力分布：

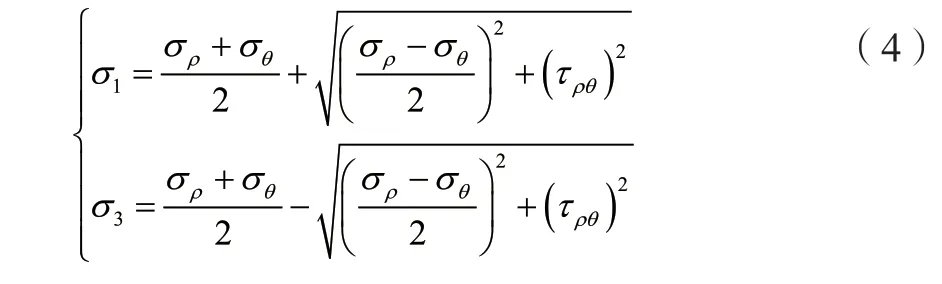
2 應力分析

淮南礦業集團潘二煤礦11221 工作面上順槽局部采用直墻半圓拱斷面巷道，使用U 型鋼進行支護，巷道斷面參數如圖2。

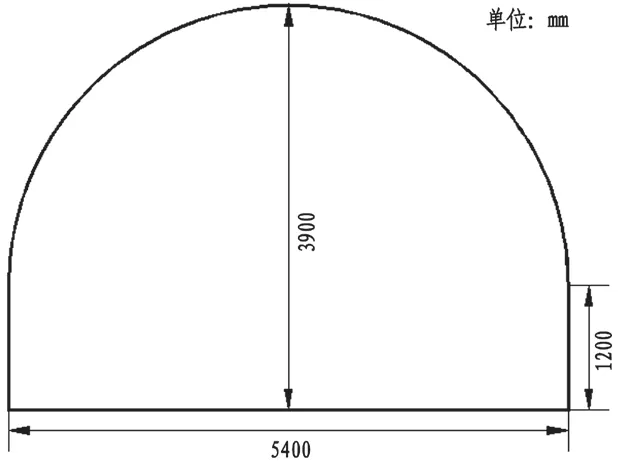
圖2 11221 工作面上順槽局部巷道斷面

11221 工作面上順槽埋深500 m 左右，參考地應力測試結果，取垂直應力σV=12.5 MPa，水平應力σH=10.2 MPa，剪應力τHV=-0.2 MPa。通過第1 節的計算，可獲得直墻半圓拱巷道圍巖主應力和主應力集中系數分布圖如圖3、圖4。

由圖3（a）和圖4（a）可知，直墻半圓拱巷道圍巖的最大主應力和最大主應力集中系數的分布規律相似。在直墻半圓拱巷道底角處，直墻半圓拱巷道圍巖的最大主應力和最大主應力集中系數達到最大值，分別超過30 MPa 和3。巷道幫部的最大主應力和最大主應力集中系數較拱頂大。最大主應力和最大主應力集中系數沿半圓拱拱角至拱頂的方向逐步減小。直墻半圓拱巷道底板中的最大主應力和最大主應力集中系數最小。

圖3 直墻半圓拱巷道圍巖主應力分布圖

圖4 直墻半圓拱巷道圍巖應力集中系數力分布圖

由圖3（b）和圖4（b）可知，直墻半圓拱巷道圍巖的最小主應力和最小主應力集中系數的分布規律相似。在直墻半圓拱巷道底角處，最小主應力和最小主應力集中系數達到最大值，分別超過20 MPa 和2。巷道圍巖表面的最小主應力和最小主應力集中系數為0。在圍巖內部，最小主應力和最小主應力集中系數逐漸增加。

由圖3（c）和圖4（c）可知，直墻半圓拱巷道圍巖的最大剪應力和最大剪應力集中系數的分布規律相似。在直墻半圓拱巷道底角處，直墻半圓拱巷道圍巖的最大剪應力和最大剪應力集中系數達到最大值，分別超過30 MPa 和10。巷道幫部和半圓拱表面的最大剪應力和最大剪應力集中系數取較大值，向圍巖深部發展，剪應力集中系數逐漸減小。巷道底板的最大剪應力和最大剪應力集中系數取值較兩幫和半圓拱小。

3 結論

本文以11221 工作面上順槽為工程背景，采用復變函數法分析了直墻半圓拱巷道圍巖的主應力和主應力集中系數的分布規律，得到以下結論：

（1）在直墻半圓拱巷道底角處，最大主應力和最大主應力集中系數達到最大值，分別超過30 MPa 和3。巷道幫部的最大主應力和最大主應力集中系數較拱頂大。最大主應力和最大主應力集中系數沿半圓拱拱角至拱頂的方向逐步減小。

（2）在直墻半圓拱巷道底角處，最小主應力和最小主應力集中系數達到最大值，分別超過20 MPa 和2。巷道圍巖表面的最小主應力和最小主應力集中系數為0。在圍巖內部，最小主應力和最小主應力集中系數逐漸增加。

（3）在直墻半圓拱巷道底角處，直墻半圓拱巷道圍巖的最大剪應力和最大剪應力集中系數達到最大值，分別超過30 MPa 和10。巷道幫部和半圓拱表面的最大剪應力和最大剪應力集中系數取較大值，向圍巖深部發展，剪應力集中系數逐漸減小。巷道底板的最大剪應力和最大剪應力集中系數取值較兩幫和半圓拱小。