基于新型倍壓單元的準Z源耦合電感高電壓增益DC-DC變換器

衛 科 周雪松 馬幼捷 李 微

1(國網晉城供電公司 山西 晉城 048000)2(天津理工大學電氣電子工程學院 天津 300384)

0 引 言

伴隨著全球性能源危機和全球變暖問題的日益嚴峻，新能源的開發與利用在世界范圍內快速推進，光伏、風能等清潔能源均得到了發展，在光伏發電并網系統中，光伏電池組在并網過程中需要用到大功率高增益的DC-DC直流變換器以解決光伏儲能裝置的電壓遠低于電網所需要的高電壓之間的矛盾。近年來，升壓變換電路的發展主要分為兩部分：隔離型與非隔離型，其中非隔離型的高增益直流變換器主要拓撲結構有開關電感、開關電容、耦合電感和由二極管和電容器組成的倍壓單元。

Boost直流變換器是經典的升壓變換器，但是其升壓增益特性有限，不適用于高功率場合。文獻[1-3]將傳統Boost的輸入電感用耦合電感代替，并將耦合電感的副邊與輸出二極管串聯，降低了變換器增益對占空比的依賴，避免變換器工作在極限占空比狀態，提高了變換器增益范圍，但是依然存在輸入電流不連續、動態元件過多等問題，不適用于光伏系統。為了解決上述問題，文獻[4]中提出了一種改進型的基于開關電容的Z源逆變器，與傳統的Z源逆變器相比，它可以實現輸入電流的連續，但升壓能力沒有提升。文獻[5]提出了準Z源結構，具有輸入電流連續、電容應力低、輸入與輸出共地等優點從而得到了廣泛的應用。

目前倍壓單元用于提高直流變換器增益的研究較為廣泛[6-7]，文獻[8]提出了一種新型的耦合電感倍壓單元，并將該單元應用在了傳統的Boost中，但其存在升壓能力有限、輸入電流不連續等問題。本文提出了一種基于新型倍壓單元的準Z源耦合電感直流變換器，顯著提升了電壓增益，減小器件應力，同時提高了變換器效率。

本文變換器拓撲如圖1所示，電路由電感L1，電容C1、C2、C3、C4，耦合電感L2、L3,二極管D1、D2、D3、D4，開關管S組成。其中耦合電感由漏感Lk、勵磁電感Lm和變比為Np∶Ns的一個理想變壓器等效[9]。

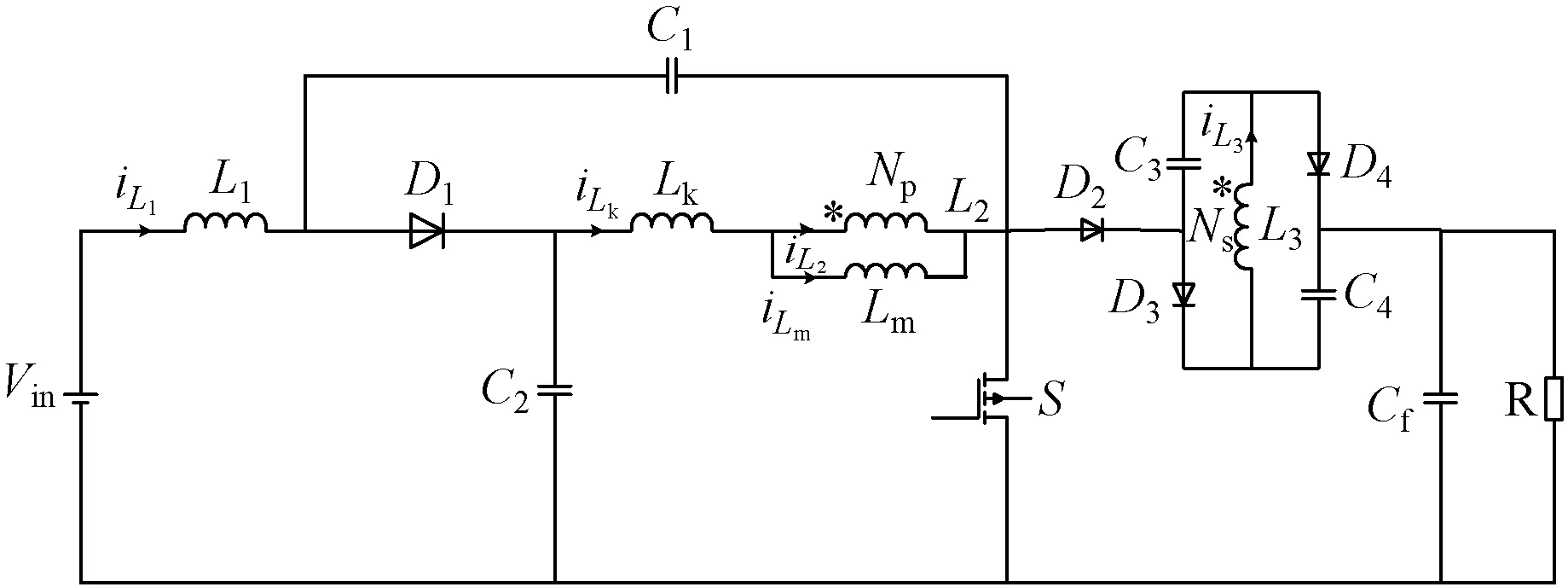
圖1 高增益直流變換器拓撲

1 電路特性分析

1.1 工作模態分析

1.1.1電感電流連續狀態

變換器工作在電感電流連續狀態時，其主要元件的工作波形和模態劃分如圖2所示。

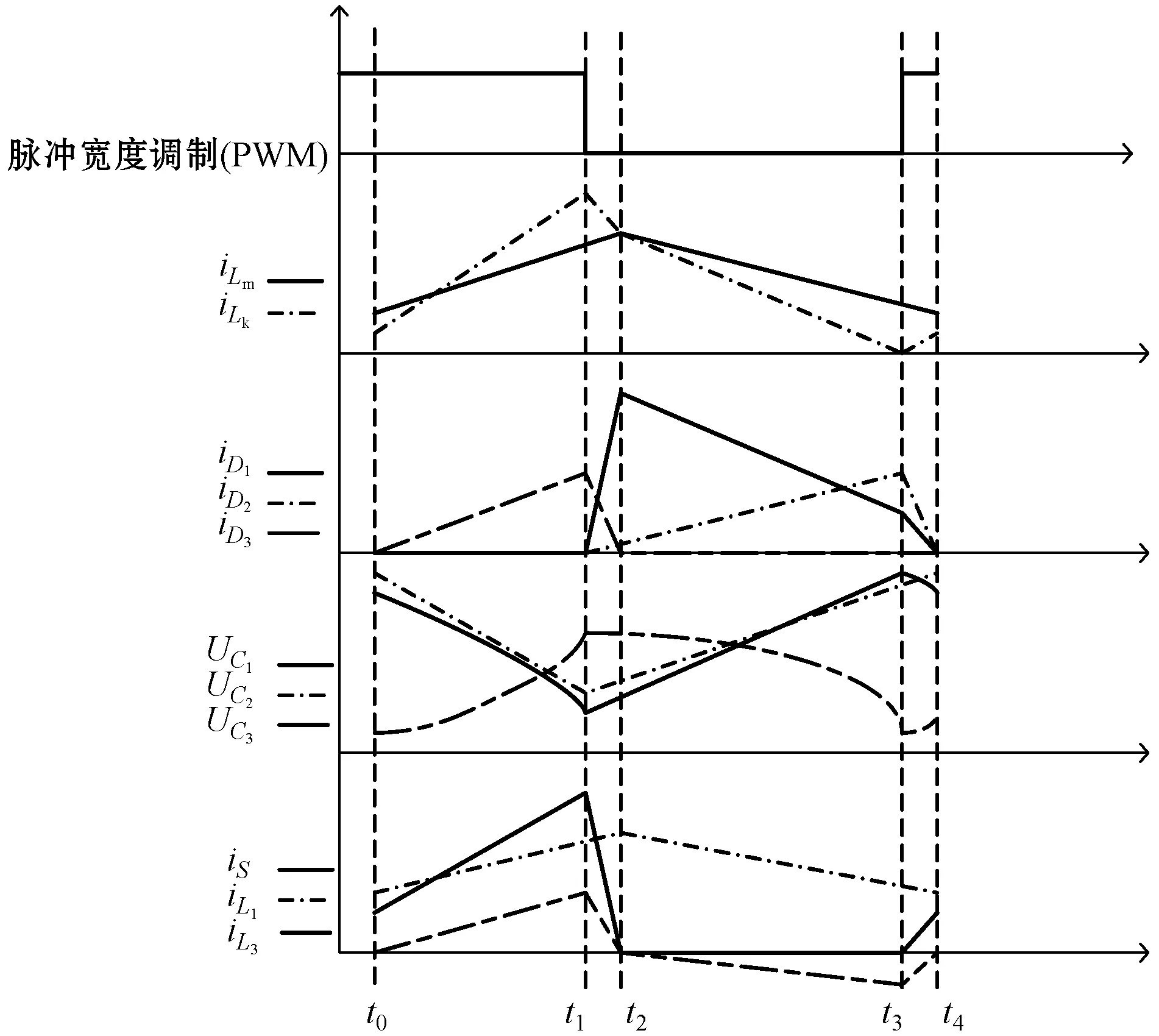
圖2 電感電流連續工作波形圖

模態1(t0-t1)：t1時刻之前，開關管S導通，在這一時間段內，輸入電壓源Vin與C1通過開關管S給電感L1儲能，C2通過開關管S向漏感Lk和勵磁電感Lm儲能，耦合電感原邊電壓左正右負，電流由同名端流入，并向耦合電感的副邊感應上正下負的電壓，產生由同名端流出的電流向倍壓電容C3、C4充電。此時間段內iL1、iLk、iLm和iL3線性上升，C1、C2電壓下降，C3、C4電壓上升，二極管D1、D2截止，D3、D4導通，負載R由電容Cf供電。

(1)

(2)

式中：N=Np∶Ns。

(3)

模態2(t1-t2)：t1時刻，控制開關管S使其關斷，上一模態的能量傳輸通道關閉，二極管D1承受正向電壓導通，由輸入電壓源Vin與C2通過D1向電感L1充電，iL1線性上升。漏感Lk向電容C1充電，漏感兩端電壓變為左負右正，勵磁電感電壓方向不變，因漏感值較小，故漏感電流減小很快，副邊耦合電感電流iL3快速減小，iLm繼續線性上升，電容C1、C2兩端電壓開始上升。

(4)

(5)

模態3(t2-t3)：t3時刻之前，開關管S仍處于關斷狀態。T2時刻,耦合電感副邊電流iL3減小為0，此時間段內副邊電流iL3反向并線性增大，勵磁電感上的電流iLm線性減小。此時二極管D2導通，D3、D4反向截止，電感L1耦合、電感的勵磁電感Lm、耦合電感副邊上的電流iL3和電容C3、C4共同向負載供電。

(6)

(7)

模態4(t3-t4)：t4時刻，開關管S導通，二極管D2處于反向恢復狀態，副邊電感上電流iL3上電流快速下降為0，二極管D1截止。電容C1電壓開始下降，漏感電流開始上升，從下一時刻開始，電路重新工作于模態1。

(8)

(9)

(10)

1.1.2電感電流斷續狀態

變換器工作在電感電流斷續模式時，其主要工作波形和模態劃分如圖3所示。

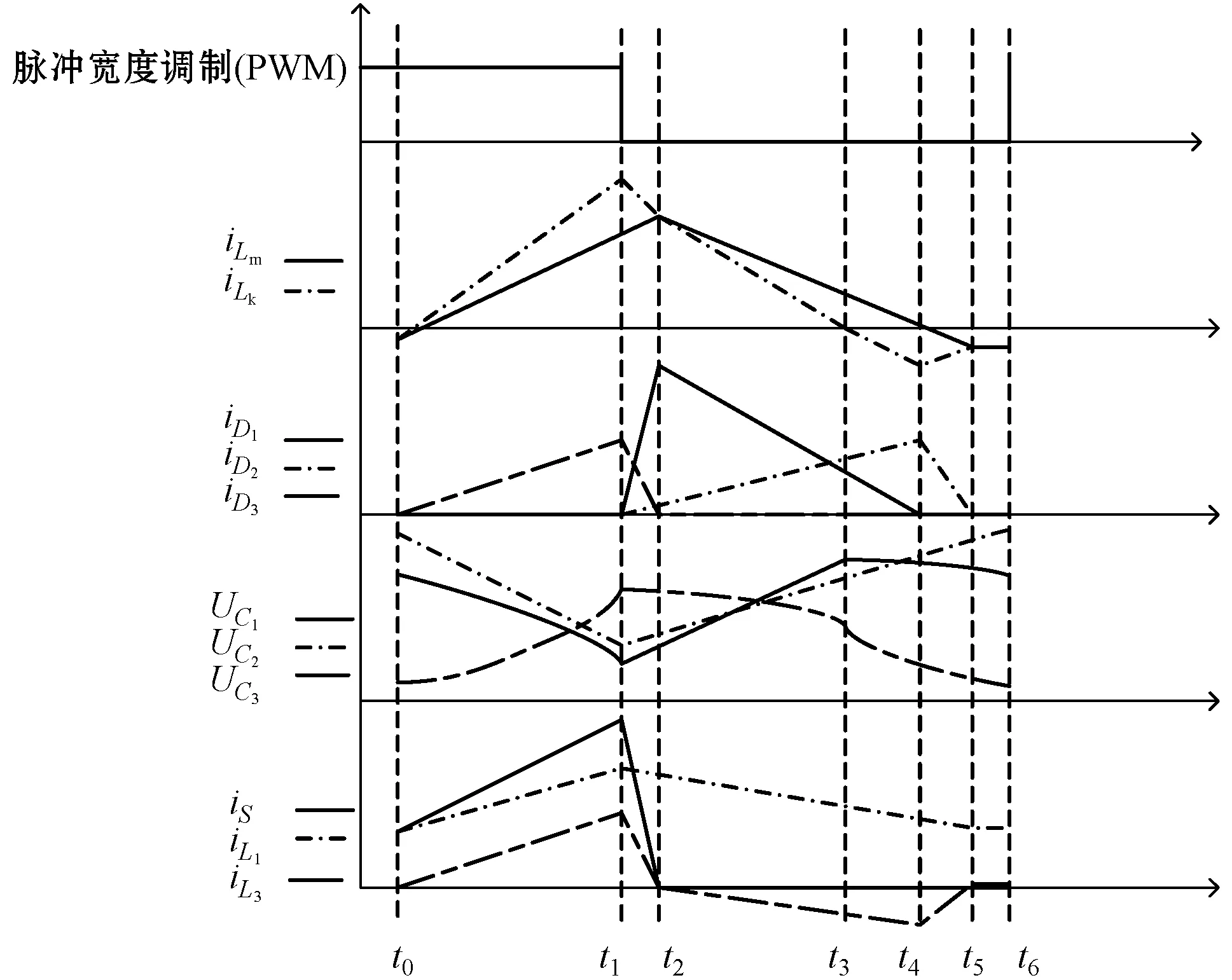
圖3 電感電流斷續工作波形圖

模態1(t0-t1)：在t1時刻之前，開關管S導通，電感L1、L2和Lk分別由輸入電源、C1和C2供電，耦合電感原邊電壓左負右正，電流從同名端流入，在耦合電感副邊產生由同名端流出的感應電流為倍壓電容C3、C4供電。此時間段內對應的電流表達式為式(1)-式(3)。

模態2(t1-t2)：在t1時刻，開關管S被控制關斷，二極管D1承受正向電壓導通，電容C1、C2分別由漏感Lk和輸入電源供電，漏感兩端電壓變為左負右正，但是勵磁電感電壓的方向不變，且電流繼續線性上升。對應電流表達式同式(4)-式(5)。

模態3(t2-t3)：開關管S仍然處于關斷狀態，t2時刻耦合電感副邊電流減小為0，然后反向并線性增大，二極管D2承受正向電壓導通，D3、D4截止，漏感與勵磁電感上的電流線性減小，電容C1、C2電壓上升，倍壓電容電壓下降，輸入電源Vin、輸入電感L1和勵磁電感Lm向負載供電。相對應的電感電壓表達式同式(6)-式(7)。

模態4(t3-t4)：t3時刻，漏感上的電流減小為0，輸入電源、L1、勵磁電感與C1向電容C2與耦合電感副邊供電，C1上的電壓開始下降，漏感上開始電流反向增加，副邊電流線性上升并繼續向負載供電。

模態5(t4-t5)：開關管S狀態不變，t4時刻，漏感電流開始反向減小，二極管D1反向截止，耦合電感副邊感應電流iL3也開始反向減小。勵磁電感上的電流減小為0并反向繼續增加。

模態6(t5-t6)：開關管S狀態不變，t5時刻，副邊電流減小到0，二極管D2反向截止。輸入電源與輸入電感L1向漏感Lk和勵磁電感充電，漏感與勵磁電感上的電流線性上升。電路工作狀態與連續模式的模態4相同。直到下一個周期到來開關管S導通，電路重新工作于模態1。

1.2 高升壓增益特性分析

根據上述的工作模態分析，可以看出工作于電感電流連續模式的新型倍壓單元和耦合電感的高增益直流變換器的四個模態中，模態2與模態4所占時間都很短，所以主要考慮模態1與模態3。由電感伏秒平衡原理，分別得到L1、L2與Lk的伏秒平衡方程式為：

(11)

式中：D為占空比；K為耦合電感的繞組系數。

由模態3可得：

V0=VC2+VC3+VC4+VC1+NVC1

(12)

由式(11)、式(12)可得：

(13)

式中：Vg為輸入電壓。

將式(13)代入式(12)得到增益M為：

(14)

1.3 器件應力分析

根據上述由增益分析可得開關管S在關斷期間的電壓應力：

(15)

則：

(16)

二極管D1、D2、D3、D4電壓應力：

(17)

(18)

(19)

綜上，相比于傳統準Z源變換器的開關管與二極管電壓應力V0/(1-D)[10]，本文提出的新型變換器的二極管應力得到了顯著的降低。

由模態分析可知，一個周期內，流經電容C3、C4的電流平均值為0，因此一個周期內耦合電感的副邊電流iL3的平均值為0，則原邊電流iL2平均值也為0，由伏秒平衡原理可得電容C1、C2上電流平均值為0，則可以得到電感L1上的電流iL1與勵磁電感電流iLm在一個周期內電流平均值為輸入電流Iin。開關管S在導通狀態下流經二極管D3、D4，在關斷狀態下流經二極管D2，由電容安秒平衡原理，可知流過二極管D2的電流平均值ID2即為輸出電流I0，同理，二極管D3、D4上的電流平均值ID3、ID4亦為I0/2，參考iL3的波形圖可得：

(20)

式中：iL3_on與iL3_off分別為副邊電流在開關管導通和關斷狀態下的峰值。iL3_on和iL3_off的計算如下：

(21)

(22)

則可以得到二極管D1、D2、D3和D4的電流應力為：

(23)

(24)

(25)

圖4為當耦合系數k=1、匝比N=3時不同變換器的電壓增益M與占空比的關系圖，可以看出，相同占空比的情況下，本文所提變換器的電壓增益顯著高于傳統的Z源變換器。

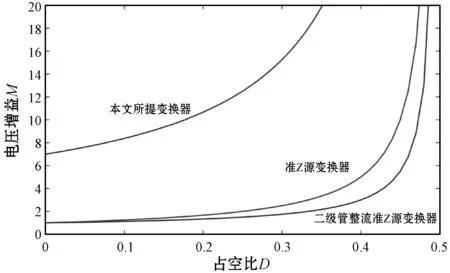
圖4 變換器增益曲線對比

1.4 電路參數設計

由增益表達式可以看出，變換器占空比應被限制在0～0.5之間，同時避免占空比在此區間內過大或過小。占空比過小，增益可能達不到所期望的值，占空比過大，由應力分析可知會導致元器件電流應力過大，電路中出現電流尖峰等對元器件產生損害并會增大損耗[11-12]。故權衡考慮電流和電壓應力，選擇占空比D=0.3，耦合電感匝比N=3。設計額定輸入電壓25 V，額定輸出電壓220 V，額定功率500 W。

1.4.1電感參數設計

準Z源直流變換器工作在電感電流連續狀態與不連續狀態的臨界條件為：

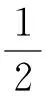
(26)

根據模態3，在開關管S導通期間，由基爾霍夫電壓定律可得：

(27)

要使變換器工作在電感電流連續模式，L1應滿足：

(28)

同理可得勵磁電感Lm應滿足：

(29)

1.4.2電容參數設計

由式(13)的電容電壓分別為：

(30)

電容器的電壓紋波為：

(31)

選擇電容C1、C2、C3、C4的電壓紋波ΔC1、ΔC2、ΔC3、ΔC4為電容電壓的1%。可得電容值為：

(32)

(33)

(34)

在選取電容器的參數時，選擇的電容值越大，則等效的串聯電阻就越小，因此考慮到損耗的因素，往往選值比上述值更大一些[13]。

1.4.3開關器件選擇

根據前面對器件應力分析式(16)可得：

(35)

開關管閉合時，開關管S的電流平均值：

(36)

則有效值為：

(37)

根據上述電壓電流應力計算，選擇開關管型號為IPP110N20N3G。

根據式(17)-式(19)可得二極管的電壓應力分別為：

(38)

根據式(23)-式(25)可得二極管電流平均值：

(39)

根據上述二極管電壓與電流的應力參數，D1選擇型號為STTH3003CW，D2選擇型號為STTH3003CW，D3、D4選型號為STTH6002C[14]。

2 功率損耗分析

2.1 MOSFET功率損耗

MOSFET的損耗主要包括兩部分：通態損耗、開關損耗。通態損耗電流有效值和導通電阻計算得到：

(40)

開關損耗分兩部分計算，首先是開通損耗：

(41)

式中：UDS為開關管S上的電壓；tr為開關管S的導通時間。

第二部分為關斷損耗：

(42)

式中：tf為開關管S關斷時間。

則MOSFET總損耗：

PMOS=P0+Pon+Poff=7.13 W

(43)

2.2 二極管損耗

二極管的功率損耗為二極管的正向壓降與二極管導通時的平均電流相乘得到：

PD=PD1+PD2+2PD3=1×20×0.7+1×3.75×

0.7+2×0.75×4.38×0.3=18.596 W

(44)

2.3 電容功率損耗

電容功率損耗主要由電容串聯等效電阻造成[15]。查詢得到470 μF與47 μF的等效串聯電阻分別為120 mΩ與50 mΩ，由RESR表示。計算可得電容功率損耗為：

(45)

(46)

(47)

電容損耗合計為：

PC=PC1+PC2+PC3=8.37 W

(48)

2.4 其他功率損耗

其他損耗主要指耦合電感的磁芯產生的損耗，常用磁芯損耗約為1.6 W，則系統磁芯損耗為3.2 W,則可得變換器效率為：

(49)

3 仿真分析

3.1 數學建模與頻域分析

為了更好地分析變換器的穩態性能和動態性能，本節將對變換器進行系統建模和頻域分析，由于變換器中含有二極管和全控型開關管等非線性元件，因此屬于非線性時變系統。但是當直流變換器工作在穩態時，其小信號變換量之間可以等效看作為線性關系。目前普遍采用狀態變量平均法對變換器進行建模，狀態空間平均法是指對非線性的系統，利用平均法的一階近似建立線性的數學模型，從而使非線性的系統可以得到線性模型，可以使用經典的線性控制理論對其進行穩態和小信號分析。

狀態空間平均法的基本思想是根據占空比將開關管不同狀態下的狀態方程進行平均化處理，以電感電流和電容電壓作為狀態變量，輸出電壓和電流作為輸出變量，建立系統平均狀態方程。

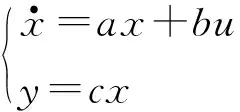
(50)

式中：x為系統狀態變量；y為輸出變量；a、b、c為未知系數。設變換器工作在穩態時(滿足低頻假設與小波紋假設)，則根據占空比對前面所分析的模態1開關管導通時的狀態方程系數A1、B1、C1與模態3開關管關斷時的狀態方程系數A2、B2、C2根據式(51)得到平均狀態方程。

(51)

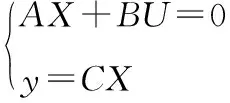
(52)

其中：

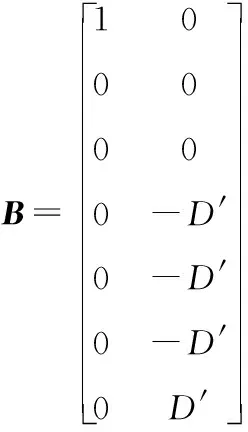
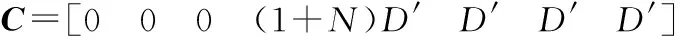
將本文變換器參數代入，由于本文變換器中儲能元件較多，為高階狀態方程，故直接求解了系統的數值表達傳遞函數如式(53)所示。

Gvs=

(53)

根據式(53)繪制系統的開環伯德圖如圖5所示。

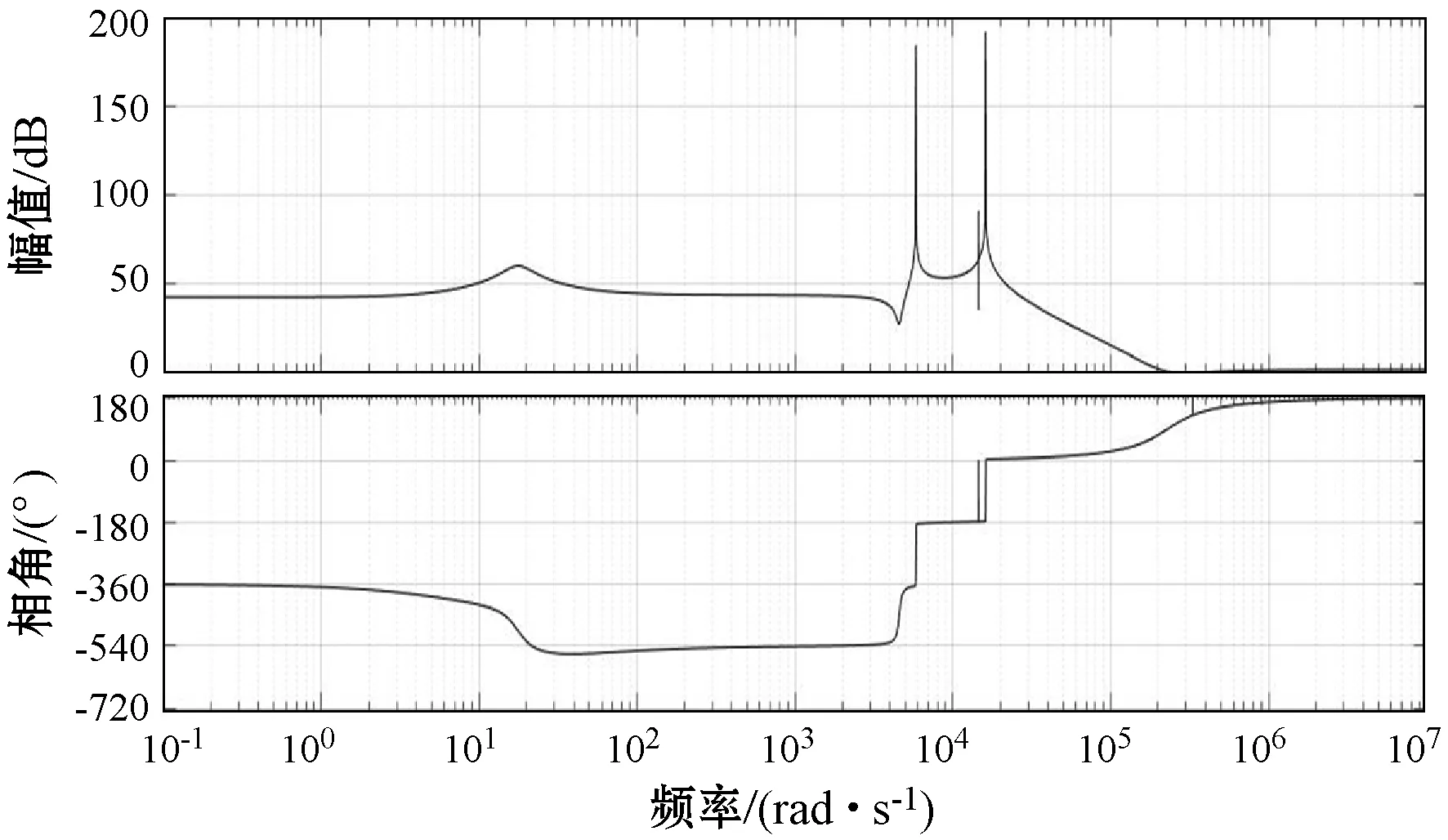
圖5 系統開環伯德圖

從圖中看到系統幅值裕度-1.94 dB，相位裕度-49.3°，不能滿足工程使用要求，根據系統開環頻域特性，為了增加變換器閉環傳遞函數的穩定性，增加系統相位裕度，綜合考慮后選擇超前校正作為其補償網絡的設計方案。

本文設計校正網絡增加增益環節，傳遞函數表達式為：

(54)

式中：α為分度系數；TS為時間常數；k為增益值。由式(54)可知，采用此補償網絡時，系統整體的增益會下降a倍，因此需要提高放大器增益用以補償。由開環頻率特性可知，系統開環相位裕度r0=-49.3°，而一般系統要求相位裕度r應該在45°左右。考慮誤差ε，根據所期望的相位裕度可得系統最大超前角度：

φm=r-r0+ε=105°

(55)

其中最大超前角度：

(56)

可以計算出：

(57)

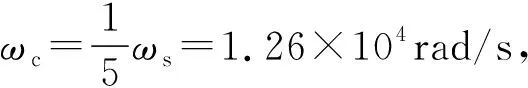
(58)

將上述的參數代入超前補償的傳遞函數中，可得不加增益補償時的傳遞函數如式(59)所示，伯德圖如圖6所示。

(59)

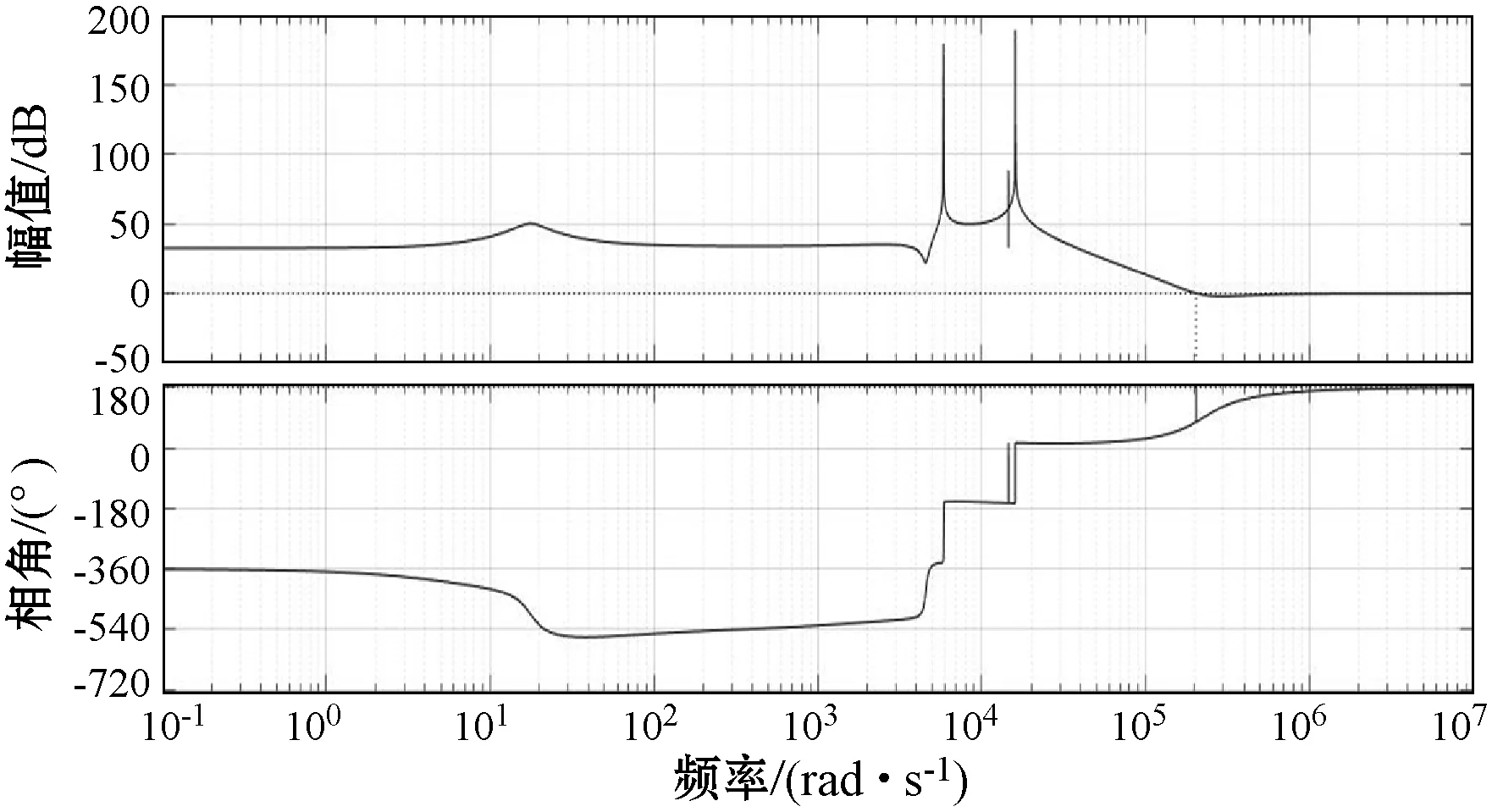
圖6 不加增益時校正后的系統伯德圖

可以看出，此時系統在期望截止頻率的增益裕量約為10 dB，由：

L(ωc)=-20lgk

(60)

可得k=0.316，則可以得到完整的校正環節傳遞函數如下：

(61)

根據伯德圖如圖7所示，可以看出，系統加入校正環節后，其相位裕度明顯改善達到了47.7°，符合期望值的45°左右，幅值裕度為13.6 dB，也是比較理想的，期望值10 dB左右，截止頻率為ωp=1.46×104rad/s，在開關頻率的五分之一左右。同時系統的穩態誤差也得到了一定程度的減小，滿足了工程應用的性能指標。

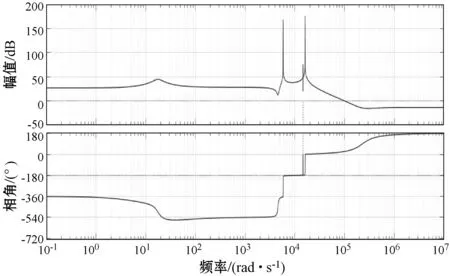
圖7 加增益校正環節后系統伯德圖

3.2 PSIM仿真

根據設定條件，經過優化的電路仿真參數如表1所示。

表1 仿真參數

根據上述參數，在仿真軟件PSIM中搭建了一個500 W的仿真模型。

圖8為輸入電壓Uin、輸出電壓U0的波形。增益效果與理論分析基本一致，當占空比為0.3時，輸出電壓約為370 V，略低于理想增益的輸出380 V，這是因為在仿真過程中加入了漏感，導致耦合電感系數降低，儲能電容的充電速率受到影響，倍壓電容沒有達到理想增壓效果。

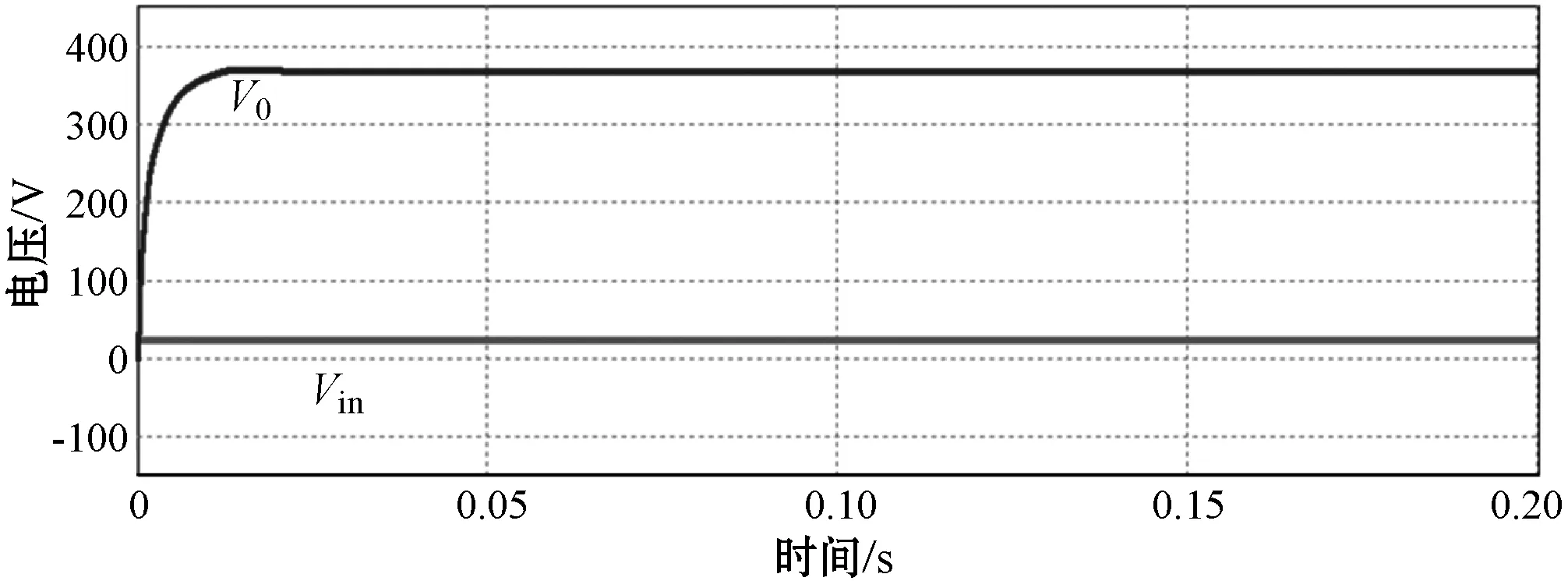
圖8 25 V輸入380 V/500 W電感電流連續模式輸出仿真圖

由圖9可見，25 V輸入、380 V/500 W輸出情況下的開關管S、二極管D1和二極管D2電流應力分別為62 V、250 V左右，與理論分析基本一致，可以看出其中開關管的電壓應力為V0/(1+N(2-D))，低于傳統準Z源耦合電感的開關管應力V0/(1+D(N-1))，輸出二極管的電壓應力為V0(1+N)/(1+N(2-D))，低于傳統準Z源耦合電感輸出二極管的應力V0。相比傳統的拓撲，本拓撲在進一步提高增益的同時降低了開關元件的電壓應力。

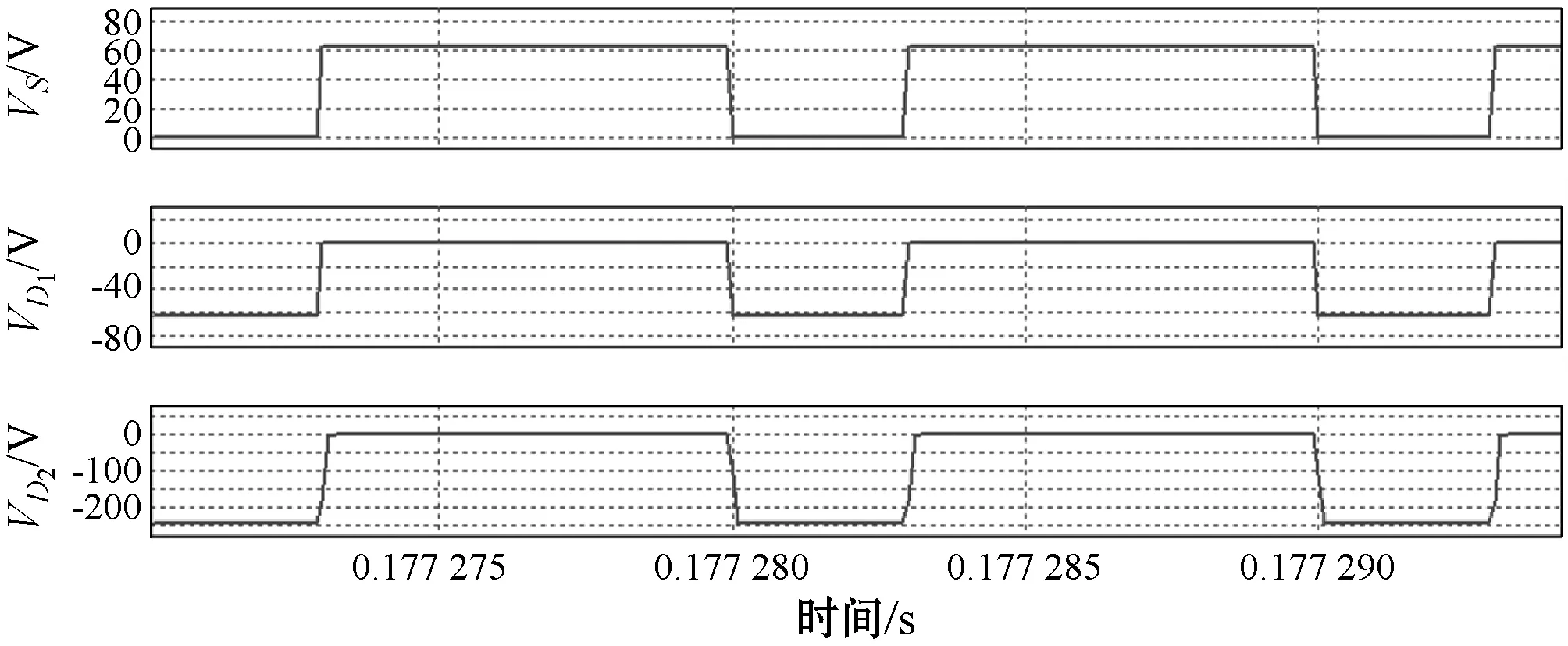
圖9 25 V輸入380 V/500 W電感電流連續模式開關元件應力仿真圖

從圖10可以看到，電容C1、倍壓電容C3、勵磁電感與漏感的工作波形，與理論分析一致，驗證了理論分析的正確性。

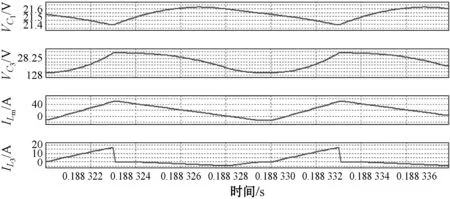
圖10 25 V輸入380 V/500 W電感電流連續模式工作波形仿真圖

圖11為電感電流斷續模式下輸入與輸出波形，也實現了理想的高增益，圖12為斷續模式下各個元件的工作模態圖，其中勵磁電感電流出現負值，輸出二極管D2提前截止，變換器工作狀態與理論分析的模態圖形一致，驗證了理論分析的正確性，也實現了電壓的高增益。

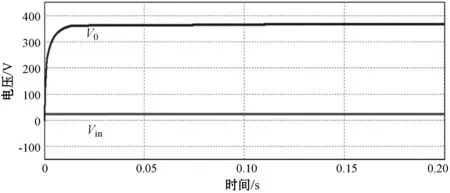
圖11 25 V輸入380 V/500 W電感電流斷續模式輸入輸出仿真圖

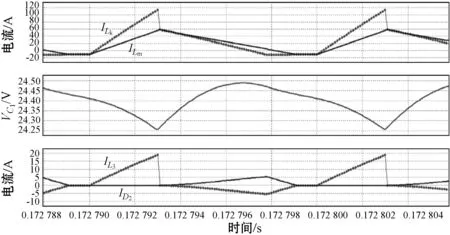
圖12 25 V輸入380 V/500 W電感電流斷續模式工作模態仿真圖

4 結 語

本文提出一種基于新型CLC倍壓單元的準Z源耦合電感高增益的非隔離直流變換器拓撲，該拓撲解決了傳統非隔離直流變換器電壓增益有限、開關元件應力大、輸入電流不連續等諸多問題。對系統進行了建模和頻域分析，驗證了系統閉環應用中的良好性能。按照500 W的PSIM仿真結果，可以看到：通過倍壓單元的改進，該拓撲在適當的占空比與耦合電感匝比情況下顯著提高了直流變換器的電壓輸出，達到了理想電壓增益，同時進一步降低了開關元件的電壓與電流應力，提高了變換器的可靠性，提高了變換器轉換效率，在電感電流連續模式下滿載效率可達93.05%。