基于有限差分法的金屬復合板冷卻過程溫度分布預測

李亞冠，王濤,2，武越，李志強，馬更生

基于有限差分法的金屬復合板冷卻過程溫度分布預測

李亞冠1a,1b，王濤1a,1b,2，武越1b，李志強1a,1b，馬更生1a,1b

（1. 太原理工大學 a. 機械與運載工程學院；b. 先進金屬復合材料成形技術與裝備教育部工程研究中心，太原 030024；2. 太原重型機械（集團）有限公司，太原 030027）

研究金屬復合板在冷卻過程中的溫度變化規律以及經過冷卻后金屬復合板的表面及內部溫度分布規律。利用二維有限差分法對金屬復合板材冷卻過程中的溫度變化規律進行了分析，從理論上推導了使用等步長節點法求解溫度的差分方程，通過設置合理的邊界條件解決了金屬復合板基板和復板接觸界面互相影響的傳熱問題。通過設置等步長節點的有限差分法計算得出金屬復合板冷卻過程的溫度變化規律以及冷卻后金屬復合板的表面及內部溫度分布，對比有限元軟件模擬計算和有限差分程序計算結果，得出結論。界面處溫度高，越靠近兩邊溫度越低，通過與有限元軟件模擬計算作對比，驗證了差分法計算的準確性。

復合板；接觸；冷卻；有限差分法；溫度場

有限差分法是工程計算中常用的一種數值計算方法，其基本思想是將求解問題的定義域劃分為有限個網格，用有限個網格節點代替連續的求解域。在網格點上利用數值微分公式把微商換成差商，從而把原定解問題離散為差分格式，進而利用計算機來進行數值求解[1]。應用于軋制領域，可求解板材加熱、軋制和冷卻過程中的溫度場變化以及軋輥在軋制和冷卻過程中的熱凸度變化等[2]。研究復合板冷卻過程的溫度分布，可以更加有效精確地制定軋制工藝，例如，確定軋件出爐到軋機的時長，以及軋后冷卻時長的控制[3—4]，精確控制軋制工藝[5]，可以得到質量更優的軋制產品。

研究表明，微觀上物體表面是粗糙不平的，因此一定載荷下，復合板基板和復板界面間的接觸是不完全接觸，實際接觸僅發生在一些離散的點或微小的面積上，其余大部分是氣體間隙或者其他雜質[5—7]，如圖1所示，a和b分別為基板和復板表面。實際應用中，將界面處的熱流傳遞方式等效為一個合理的接觸換熱系數來進行計算[8]，該系數大小與基板和復板的導熱系數、接觸面積、界面壓力以及界面溫度等都有關系，至今仍無法用理論公式進行精確計算，通常取值為10～30 kW/(m2·K)[9—10]。

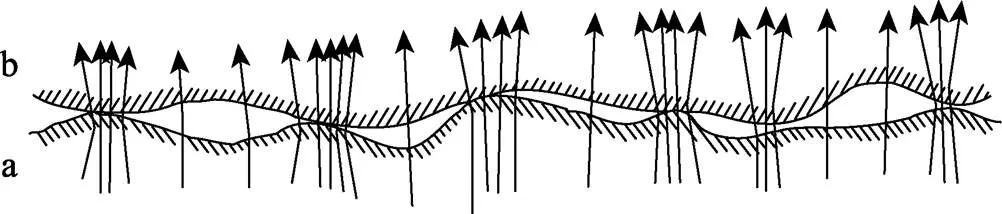
圖1 復合板接觸面附近熱流變化

1 二維導熱微分方程

對于穩態傳熱，二維導熱微分方程可表示為[11]：

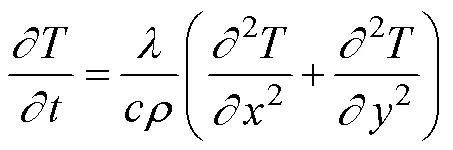
式中：為溫度（℃）；為時間（s）；為導熱系數（W/(m2·℃)）；為密度（g/cm3）；為比熱容（J/(kg·℃)）；，為坐標。

有限差分法包括顯式差分和隱式差分2種方式，其中顯式差分法每個節點方程均可獨立求解，而隱式差分法需聯立每一層各個節點的方程組才可求解[12]，因顯式差分法計算簡便，因此文中采用等步長顯式差分法來求解復合板冷卻過程的溫度變化。

2 等步長顯示差分法

等步長顯式差分法中的等步長是指劃分單元格的大小相等。實際生產中軋制所需的復合板，板材長度遠大于其寬度和厚度，因此，計算復合板冷卻過程的溫度變化時，只考慮復合板寬度和厚度方向，利用二維有限差分法來計算冷卻過程的溫度變化。

對式（1）進行差分處理后得：

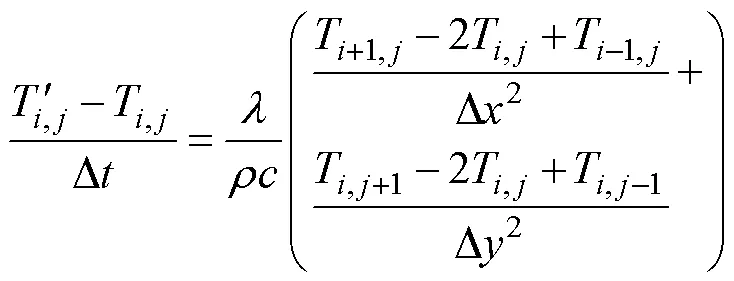
式中：T,j為節點（，）的當前溫度（℃）；T',j為節點或者單元（，）冷卻Δ時間后的溫度（℃）；Δ為時間步長（s）；Δ和Δ分別為和方向上的空間步長（mm）。

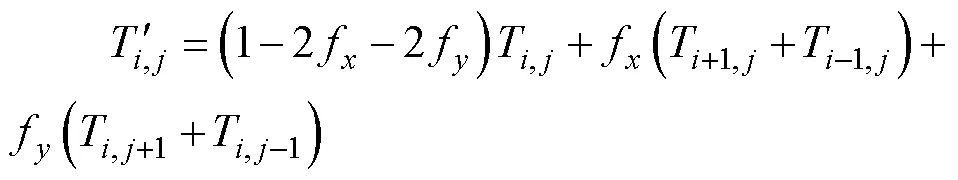
如圖2所示，ABE1F1指基板，E2F2DC指復板，沿x軸（復合板寬度）方向平均劃分為m個單元，單元大小為，節點總個數為m+1個，沿y軸（復合板厚度）方向平均劃分為n個單元，單元大小為，節點總個數為n+1個。圖2中直線箭頭表示中心節點向接觸界面節點傳熱情況，曲線箭頭表示復合板表面向空氣散熱情況。

該方法中，采用基板和復板分別劃分網格的方式。為了簡化計算，基板和復板寬度方向劃分相等的節點數。板材頂點處為1/4個單元大小，邊界處為1/2個單元大小。計算基板和復板接觸界面溫度時，分別以對方接觸邊界的溫度作為自身的邊界條件，實現界面處溫度互相傳遞的計算，計算時假設界面接觸換熱系數為一常數。

假設復合板外表面與外界環境為均勻冷卻，考慮到輻射傳熱和與空氣的對流換熱[13]，推導出復合板表面與空氣接觸的邊界條件為：

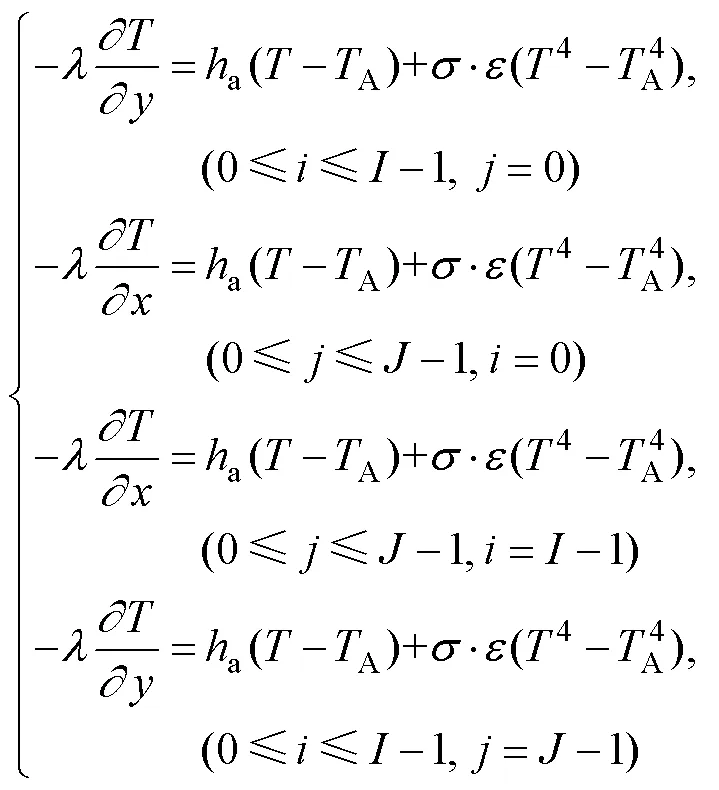
式中：A和分別為空氣溫度和復合板外表面溫度（K）；為復合板寬度方向節點數；為復合板厚度方向總節點數；a為與空氣的換熱系數（W/(m2·℃)）；為輻射率，文中取0.8；為Stefan-Boltzmann常數，文中取5.67×10?8W/(m2·K4)。根據以上條件，推導出以下的差分方程：

1）基板內部：

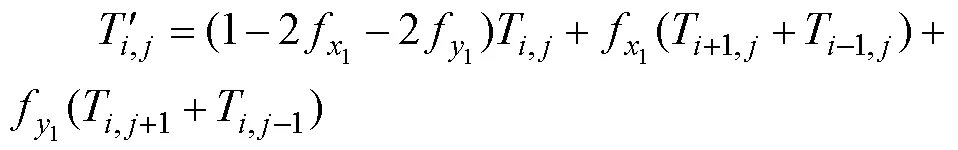
2）復板內部：

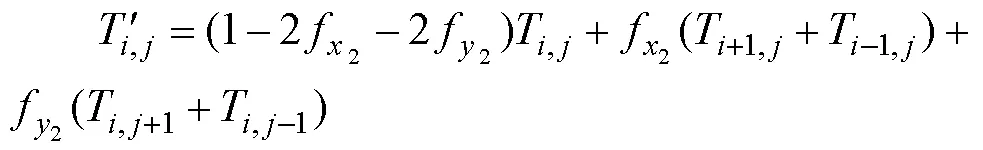
3）基板外表面：

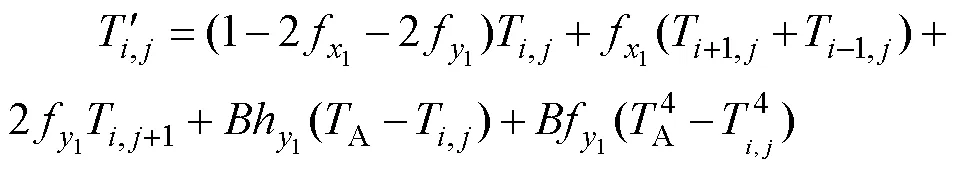
4）接觸位置基板表面：

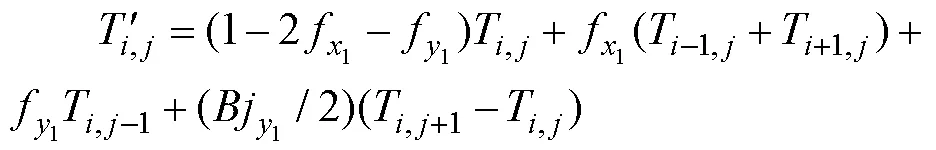
5）接觸位置復板表面：

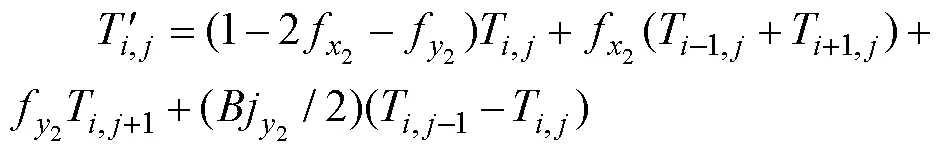
6）復板外表面：

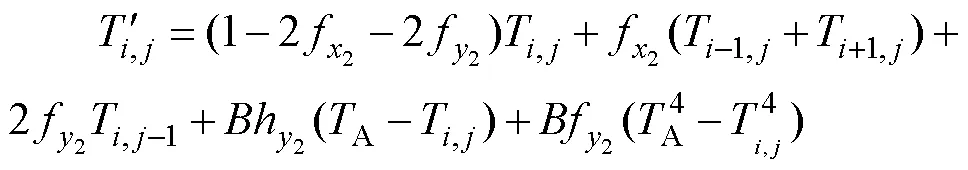
7）基板外部頂點：

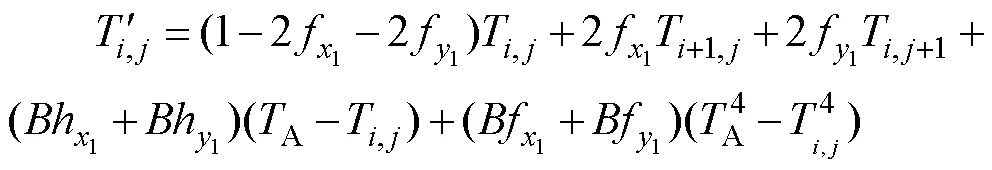
8）接觸位置基板頂點：

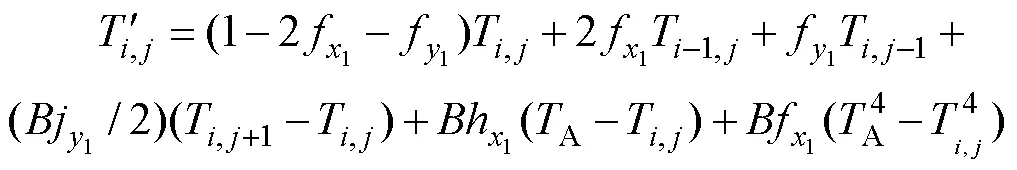
9）接觸位置復板頂點：

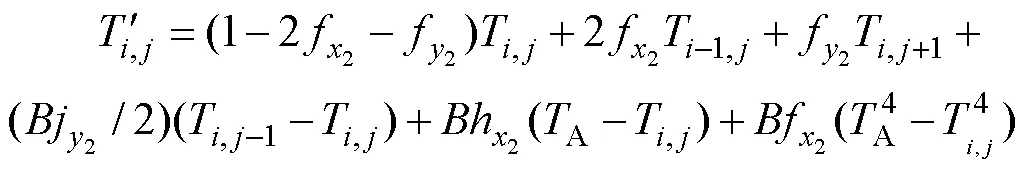
10）復板外部頂點：

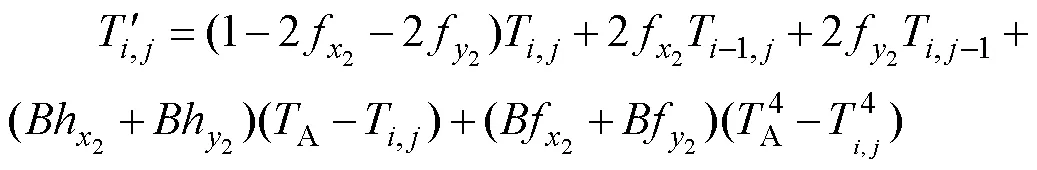
為了保證算法收斂，時間步長需滿足以下條件：

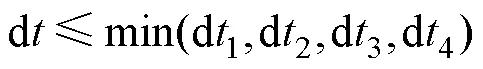
式中：

3 計算分析

基于Microsoft Visual Studio平臺，采用C#[14]語言編寫了復合板冷卻過程溫度變化的計算程序，計算方法為有限差分法。基板的寬度和厚度分別為400 mm和20 mm，寬度和厚度方向步長分別為20 mm和2.5 mm，時間步長為0.02 s，其余計算參數如下：密度為7.8 g/cm3，比熱容為662 J/(kg·℃)，導熱系數為300 W/(m·℃)，復板的寬度和厚度分別為400 mm和10 mm，寬度和厚度方向步長分別為20 mm和2.5 mm，時間步長為0.02 s。其余計算參數如下：密度為7.8 g/cm3，比熱容為462 J/(kg·℃)，導熱系數為60 W/(m·℃)，空氣換熱系數為30 W/(m·℃)，界面換熱系數為30 000 W/(m·℃)，基板復板的初始溫度為1250 ℃，空氣溫度為25 ℃，冷卻時間為20 s。

基于以上參數，利用有限元模擬軟件ABAQUS，采用顯示算法，計算了復合板冷卻過程的溫度變化，模擬時復合板界面處作如下處理：建立二維模型時，基板和復板界面分別用各自的邊界，并且保證基板和復板沿寬度方向劃分相同的單元數[14—15]，單元格的劃分方式如圖3所示。為了驗證該有限差分法計算的準確性，假設一個固定的界面接觸換熱系數進行計算。

圖3 復合板網格劃分

3.1 計算時間

采用相同的時間步長進行計算，有限差分法計算時間為1.406 s（程序運行時間），而有限元模擬時間為44 s（軟件計算時間），可以看出有限元模擬計算所需時間遠遠大于有限差分法程序的運算時間。

3.2 計算結果

3.2.1 溫度隨時間變化變化

基板表面和復板表面及兩板材接觸界面處溫度隨時間的變化情況如圖4所示，復合板不同位置處的溫度均隨冷卻時間的增加而減小。從圖4可以看出，有限差分法與有限元模擬的結果曲線幾乎重合，說明2種方法計算結果比較吻合。

3.2.2 溫度沿寬度方向變化

為了進一步對比等節點有限差分法與有限元模擬結果之間的差別，用冷卻后溫度在復合板不同位置沿寬度方向的分布情況來進行說明，沿寬度方向的溫度分布如圖5所示，給出了冷卻以后基板表面、復板表面和接觸界面處溫度沿寬度方向的分布情況。復合板不同位置處沿板材寬度的分布均呈現中心高，邊部低的趨勢。從圖5可以看出，有限差分法與有限元模擬的結果曲線幾乎重合，吻合度較高，誤差較小。

復合板冷卻后整體溫度分布云圖如圖6所示，可知，不同方法得出的復合板冷卻后溫度分布云圖是一致的。對比冷卻之后每種方法每個節點的溫度值可知，有限差分法計算的結果與有限元模擬的結果溫度差值最大不超過3.31 ℃，再次說明等步長差分法的計算結果與有限元模擬的結果比較吻合。

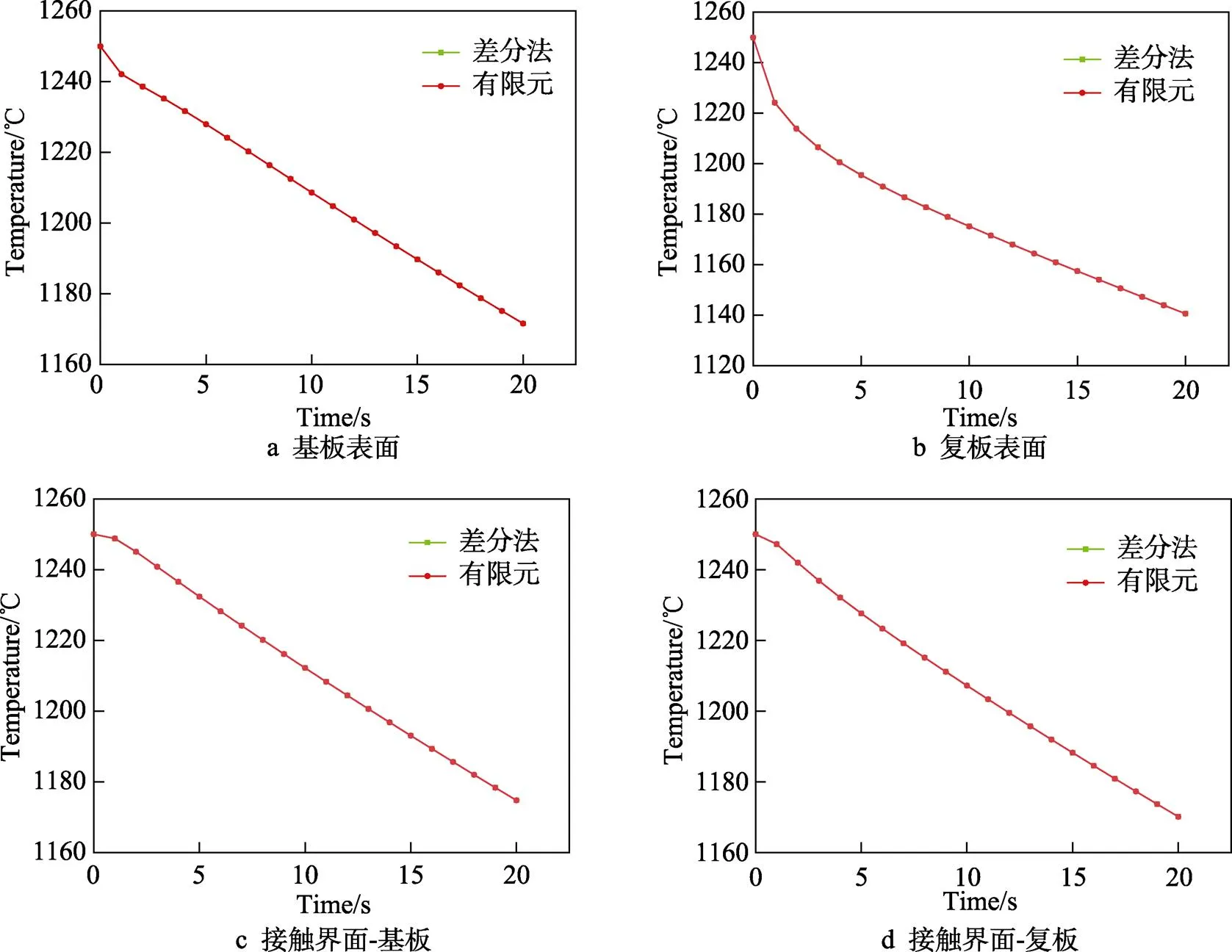
圖4 采用不同方法計算復合板不同位置溫度隨時間變化情況

圖5 復合板冷卻后不同位置處沿寬度方向的溫度分布

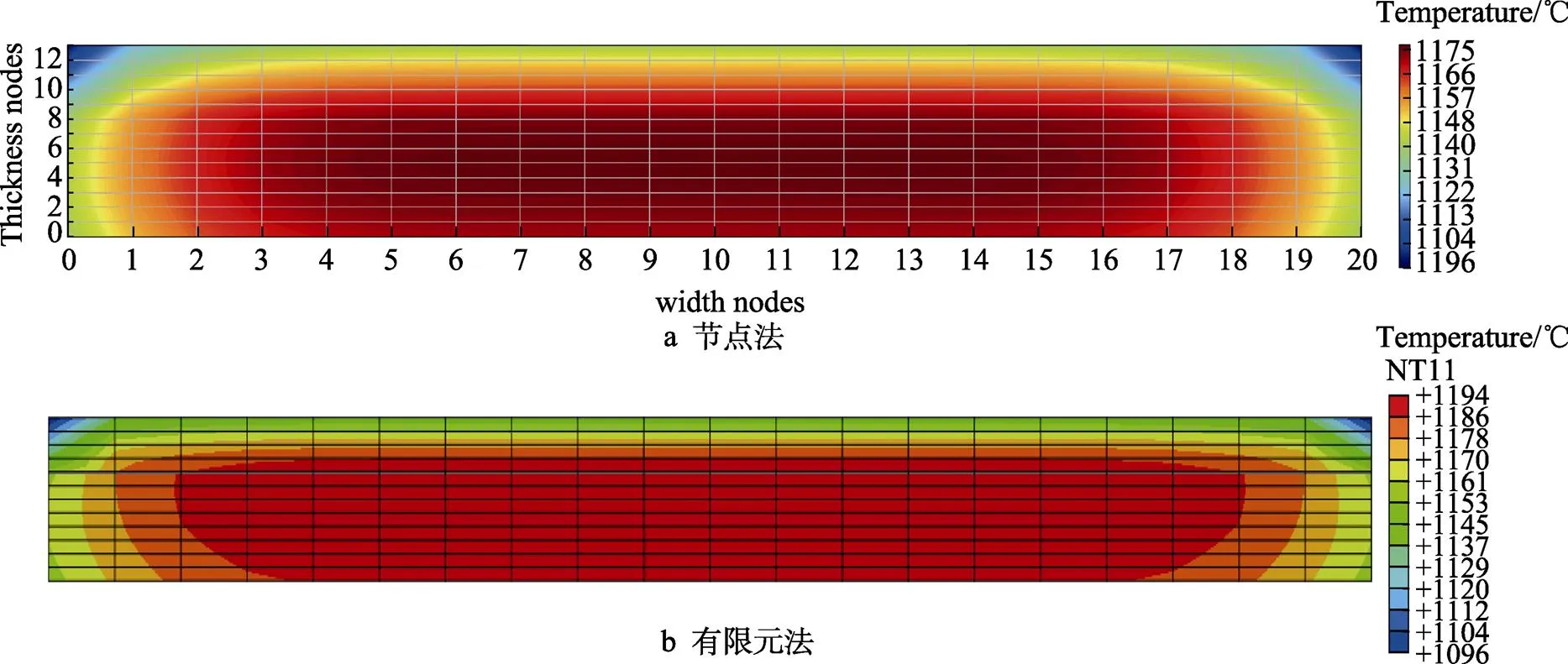
圖6 采用不同方法計算復合板冷卻后的溫度分布云圖

4 結論

1）采用基板復板邊界溫度互為對方邊界條件的方式，差分法計算和有限元模擬所得的溫度分布結果一致。

2）從運算時間來看，利用有限差分法編寫程序計算的時間遠小于有限元模擬計算所需的時間，并且差分法算法簡單，占用計算機內存較小。

3）綜上所述，利用有限差分法計算復合板冷卻溫度變化時，不僅算法簡單、用時短、占用計算機內存小，而且計算結果比較精確，因此在實際軋制過程中，可優先考慮采用等步長節點法來進行計算。

[1] 辛啟斌. 材料成型計算機模擬[M]. 北京: 冶金工業出版社, 2006: 5—15.

XIN Qi-bin. Computer Simulation of Material Forming[M]. Beijing: Metallurgical Industry Press, 2006: 5—15.

[2] 王濤. 熱軋帶鋼板凸度和板形計算及預設定建模理論研究[D]. 秦皇島: 燕山大學, 2012: 38—43.

WANG Tao. Theory Research on Strip Crown and Shape Calculation and Pre-set Modeling in Hot Rolling[D]. Qinhuangdao: Yanshan University, 2012: 38—43.

[3] 韓東序, 杜林秀, 吳紅艷, 等. 軋后冷卻速率對GCr15軸承鋼球化組織的影響[J]. 東北大學學報(自然科學版), 2019, 40(10): 1392—1397.

HAN Dong-xu, DU Lin-xiu, WU Hong-yan, et al. Effect of Cooling Rate on Spheroidized Microstructure of GCr15 Bearing Steel[J]. Journal of Northeast University (Natural Science Edition), 2019, 40(10): 1392—1397.

[4] BHADESHIA H. Steels for Bearings[J]. Progress in Materials Science, 2012, 57(2): 268—435.

[5] 李大偉, 張磊, 周遠航, 等. 2014鋁合金軋制工藝研究[J]. 熱加工工藝, 2020, 49(3): 110—112.

LI Da-wei, ZHANG Lei, ZHOU Yuan-hang, et al. Research on Rolling Process of 2014 Aluminum Alloy[J]. Hot Working Technology, 2020, 49(3): 110—112.

[6] 朱德才, 張立文, 裴繼斌, 等. 固體界面接觸換熱系數影響因素的實驗研究[J]. 鍛壓技術, 2008, 33(1): 139—142.

ZHU De-cai, ZHANG Li-wen, PEI Ji-bin, et al. Experimental Research of Influence Factors on Solid Interface Thermal Contact Conductance Coefficient[J]. Forging & Stamping Technology, 2008, 33(1): 139— 142.

[7] 石零. 低溫固-固接觸界面熱傳輸研究[D]. 武漢: 華中科技大學, 2006: 66—81.

SHI Ling. The Investigation of Solid-Solid Contact Interface Thermal Transfer[D]. Wuhan: Huazhong University of Science and Technology, 2006: 66—81.

[8] TANG Q, HE J, ZHANG W. Influencing Factors of Thermal Contact Conductance between TC4/30CrMnSi Interfaces[J]. International Journal of Heat and Mass Transfer, 2015, 86: 694—698.

[9] 陳國學, 胡煒, 耿健. 復雜鍛件凈成形過程溫度場的數值模擬[J]. 塑性工程學報, 1998, 10(4): 62—67.

CHEN Guo-xue, HU Wei, GENG Jian. Numerical Simulation of Temperature Fields in Net Shape Forming Process of Complex Forgings[J]. Journal of Plasticity Engineering, 1998, 10(4): 62—67.

[10] 朱智, 張立文, 顧森東. TC11鈦合金與5CrMnMo模具鋼間接觸換熱實驗研究[J]. 大連理工大學學報, 2012(4): 509—513.

ZHU Zhi, ZHANG Li-wen, GU Sen-dong. Experimental Investigation of Contact Heat Transfer between TC11 and 5CrMnMo Die Steel[J]. Journal of Dalian University of Technology, 2012(4): 509—513.

[11] 梁勛國, 韓會全. 二維顯式有限差分方法研究[J]. 鋼鐵技術, 2012(2): 19—29.

LIANG Xun-guo, HAN Hui-quan. Research on Two-Dimensional Explicit Finite Difference Method[J]. Steel Technology, 2012(2): 19—29.

[12] 陶文銓, 楊世銘. 傳熱學[M]. 北京: 高等教育出版社, 1982: 147—180.

TAO Wen-quan, YANG Shi-ming. Heat Transfer[M]. Beijing: Higher Education Press, 1982: 147—180.

[13] 陳超超, 邵健, 何安瑞. 熱軋帶鋼溫度場在線計算方法研究[J]. 機械工程學報, 2014(14): 135—142.

CHEN Chao-chao, SHAO Jian, HE An-rui. Research on Online Calculation Methods of Temperature Field of Hot Strip[J]. Journal of Mechanical Engineering, 2014(14): 135—142.

[14] 譚浩強. C程序設計(第四版)[M]. 北京: 清華大學出版社, 2010: 85—165.

TAN Hao-qiang. C Programming (Fourth Edition)[M]. Beijing: 2010: 86—165.

[15] 李世蕓, 張曙紅, 張代明. 雙金屬復合帶材軋制過程有限元模擬[J]. 中國有色金屬學報, 2001, 11(6): 1075.

LI Shi-yun, ZHANG Shu-hong, ZHANG Dai-ming. Finite Element Simulation of the Rolling Process of Bimetallic Composite Strip[J]. The Chinese Journal of Nonferrous Metals, 2001, 11(6): 1075.

Prediction of Temperature Distribution of Metal Composite Plate during Cooling Process Based on Finite Difference Method

LI Ya-guan1a,1b, WANG Tao1a,1b,2, WU Yue1b, LI Zhi-qiang1a,1b, MA Geng-sheng1a,1b

(1. a. College of Mechanical and Vehicle Engineering; b. Engineering Research Center of Advanced Metal Composites Forming Technology and Equipment, Taiyuan University of Technology, Taiyuan 030024, China; 2. Taiyuan Heavy Machinery (Group) Co., Ltd., Taiyuan 030027, China)

The work aims to study the temperature change law of metal composite plate during cooling and the distribution law of surface and inside temperature after cooling. The two-dimensional finite difference method was used to analyze the law of temperature change of metal composite plate during cooling, and the difference equation for solving the temperature by equal-step node method was theoretically derived. Reasonable boundary conditions were set to solve the heat transfer problem of the interaction between the metal composite plate substrate and the contact interface of the composite plate.Through the finite difference method with equal-step node, the law of temperature change of the metal composite plate during cooling and the distribution of surface and inside temperature after cooling were calculated. By comparing the simulation results of finite element software with those of finite difference program, a conclusion was drawn. The interface temperature is high, but the temperature closer to both sides is lower. Compared with the simulation calculation by finite element software, the accuracy of the difference method is verified.

composite plate; contact; cooling; FDM; temperature field

10.3969/j.issn.1674-6457.2021.06.008

TG335.81

A

1674-6457(2021)06-0064-06

2021-07-01

國家自然科學基金（51905372）

李亞冠（1995—），男，碩士生，主要研究方向為復合板軋制工藝。

王濤（1985—），男，博士，教授，主要研究方向為軋制工藝與智能裝備。