抗差在GPS/BDS 組合定位中的作用分析

韓澎濤 丁新展 施佳慧

（1、泰山科技學院，山東泰安 271000 2、沈陽市勘察測繪研究院有限公司，遼寧沈陽 110000）

精密單點定位（Precise Point Positioning, PPP）作為新興起的定位方式被廣泛的應用于各種實際問題當中，例如工程測量、變形監測和衛星定軌等[1-2]。在日常應用中所測得的數據難免伴隨著各種誤差，為了控制誤差對定位結果的影響，學者們提出了多種有效的抗差方法，從最初的數據探測法到后續的Huber 法、丹麥法和IGG 法，所有抗差方法存在共性，便都是計算等價權矩陣。

本文針對城市環境下，定位結果受噪聲影響嚴重情況進行研究。主要利用實測數據在雙頻無電離層組合模型下進行PPP，并對數據探測法和IGG III 模型的抗差能力進行研究。

1 數據處理原理

1.1 雙頻無電離層組合定位模型

1.2 抗差模型

數據探測法于1968 年被荷蘭學者巴爾達（Baarda）教授提出。假定一個平差系統僅存在一個粗差是數據探測法的核心思想，通過統計檢驗的方法剔除該粗差，在剔除第一個粗差后進行循環迭代剔除下一個粗差，直至認定該系統不存在粗差后再進行平差。

相較于數據探測法IGG 抗差模型應用更廣，將觀測數據分劃為三類，通過三段式函數進行定權[6]。將觀測值分置三個區域，分別是拒絕區、降權區和保權區。目前由國內學者提出的IGG III 方案應用最為廣泛，相比于傳統IGG 法具備有界、分段、高效和連續的特性。可以充分的利用到準確觀測值和可疑觀測值，并達到抑制異常值對結果造成影響的作用，可以起到顯著的抗差效果。改進后的IGG III 權函數為：

式中，vi為標準化殘差；pi和pi分別為等價權矩陣和原始權矩陣；c0和c1為調和系數，一般c0取1.0～1.5，c1取2.0～3.0。

2 數據源與處理策略

本文抗差實驗涉及到靜態和動態兩個部分，分別在小區廣場一側（gcyc）、“T”型路口（txlk）和橋邊（ylqb）處采集了靜態觀測數據。將接收機安置在手推車上，并在運動場上進行動態數據采集，數據處理中所需的精密數據均從IGS 數據中心下載。數據具體處理策略如表1 所示。

表1 算法策略

3 實驗結果分析

首先，利用gcyc、txlk 和ylqb 測站觀測數據分別在不抗差、數據探測法抗差和利用IGG III 模型抗差三種策略下進行GPS/BDS 組合靜態PPP 解算。以gcyc 測站定位結果為例，三種情況下的定位誤差如圖1 所示。

通過圖1 可明顯看出，當利用gcyc 測站觀測數據進行靜態PPP 時，若不考慮異常觀測值帶來的影響，定位精度受到嚴重影響；當利用數據探測法或IGG III 進行抗差時，定位精度均得到巨大提升。以0.15 m 為定位誤差收斂標準的閾值，將各測站的收斂時間與定位精度進行統計如表2 所示。

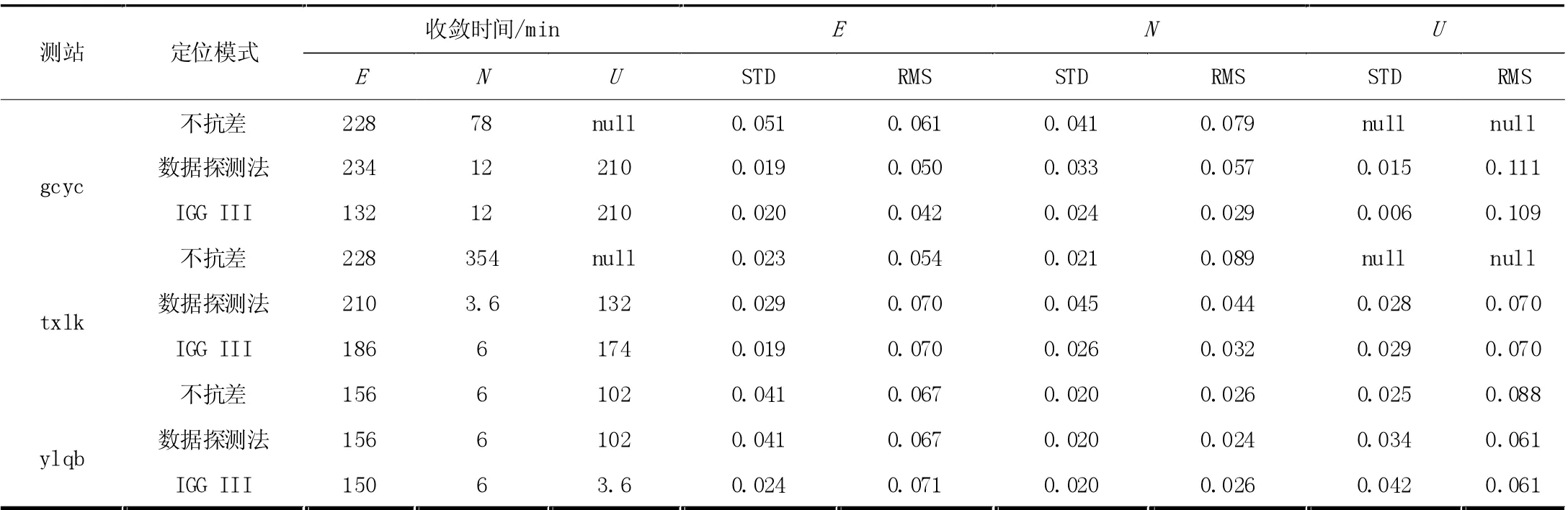
表2 不同抗差模式下定位誤差統計

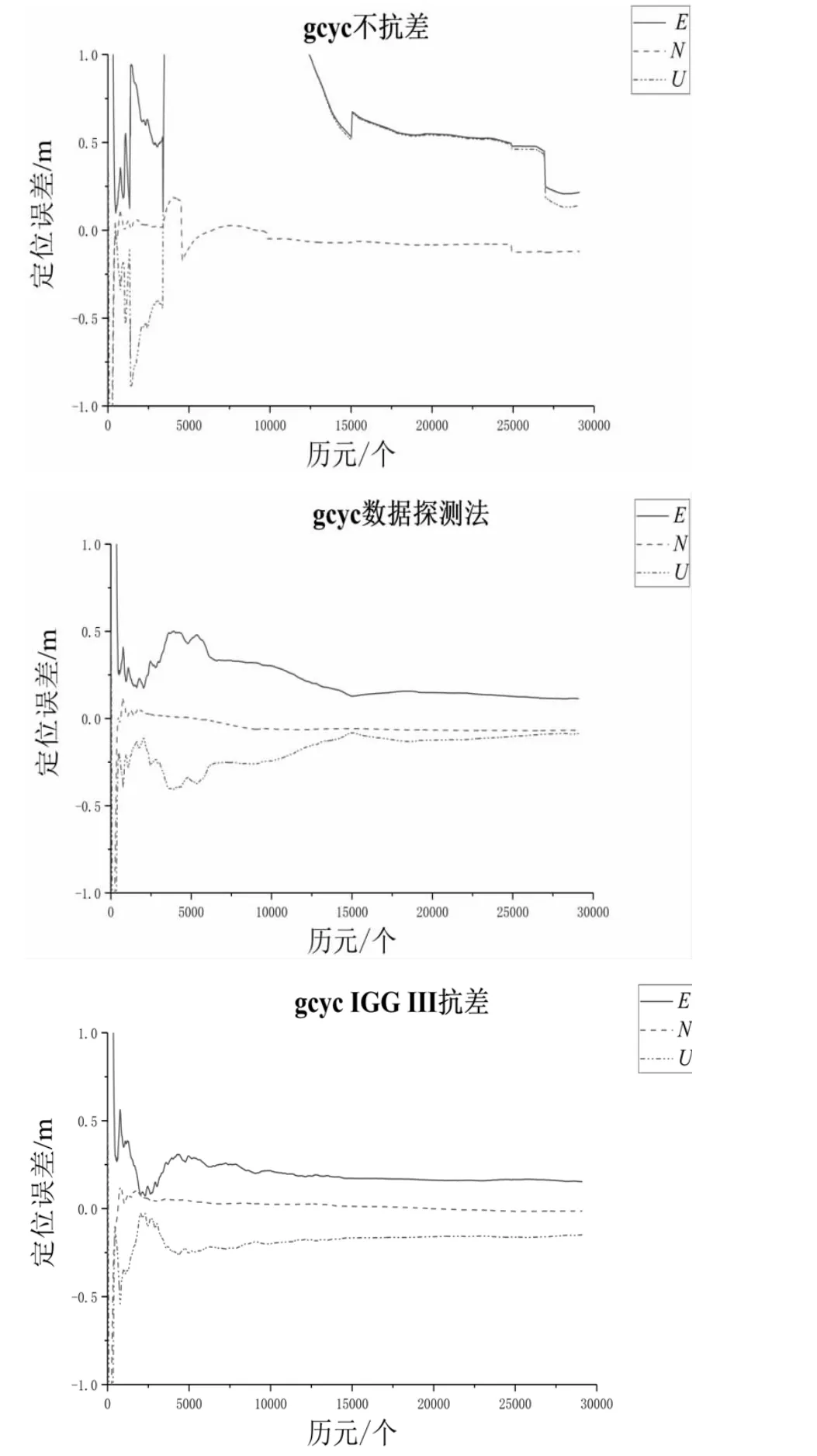
圖1 gcyc 測站不同抗差模式下定位誤差對比

就測站環境而言，三個測站當中gcyc 測站環境差，DOP 值為2.5，多路徑RMS 為0.31 m，從定位結果上更易展現出抗差策略差異。通過表1 對該測站在不同抗差模式下定位結果進行統計分析，發現gcyc 測站在IGG III 策略下E 方向收斂時間較數據探測法策略下縮短43.5%，N 與U 方向收斂時間基本一致；收斂后IGG III 策略下N 和U 方向定位誤差的STD 較數據探測法分別減小了27%和60%，E 方向定位精度基本一致；E 和N方向定位誤差的RMS 分別減小了16%和49.1%，U 方向基本保持一致。txlk 與ylqb 測站均在IGG III 抗差模式下收斂時間最短定位精度最高。綜上所述，在定位解算時必須考慮粗差對定位結果的影響，尤其是城市環境下實測數據。若不考慮異常觀測值帶來的影響將導致收斂時間較長，定位精度較差。數據探測法與IGG III 均能滿足導航定位中抗差需求，但IGG III 策略使得正常觀測值與異常觀測值均得到有效利用，該策略下收斂速度更快定位精度更高，與數據探測法相比IGG III 更適用于靜態PPP 解算。

為體現IGG III 在動態定位中的能力，現利用實測動態測站tcl1 的觀測數據進行GPS/BDS 組合動態PPP 實驗，將兩種方案下E、N 和U 方向定位誤差進行對應統計繪圖，結果如圖2 所示。

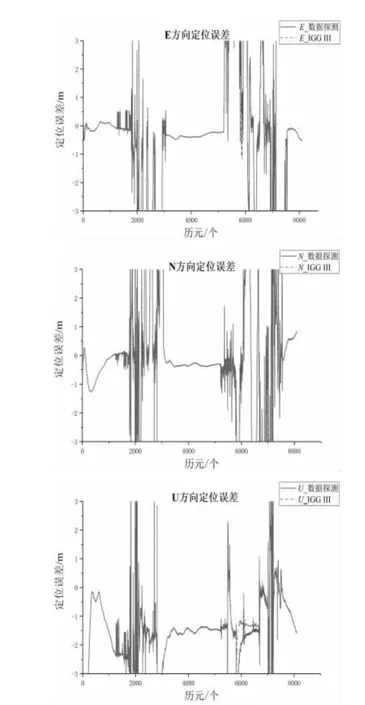
圖2 tcl1 測站不同抗差模式下動態定位結果

從圖2 中可以看出利用兩種抗差模型后，E 和N 方向上的定位誤差基本一致，經定位結果統計發現兩種策略下E 和N 方向定位誤差相差不足1%；U 方向定位精度在IGG III 策略下有所提升，U 方向定位誤差的STD 和RMS 分別減小了3.8%和2.2%。從圖2 中看出U 方向定位精度提升主要體現在6000 至7000 歷元之間，對該時段內可觀測到衛星數和殘差進行統計分析，發現該時段內可觀測到衛星數較少，平均每個歷元僅能觀測到7 顆衛星，且觀測數據質量不佳存在粗差，利用IGG III 策略抗差時對觀測質量不佳的衛星進行降權處理，而數據探測法對此類衛星直接剔除，致使可用衛星數更少，空間幾何構型更差。因此在IGG III 策略下定位精度得到提升。綜上所述，無論是靜態定位還是動態定位，數據探測法和IGG III 均能起到抗差提升定位精度的作用，且利用IGG III 后定位精度和收斂速度均高于數據探測法，主要在于IGG III 對異常觀測值的合理利用；同時證實了IGG III 在現代導航定位中應用較廣的原因。

4 結論

經過實驗發現，與數據探測法這種剔除含有粗差的衛星抗差策略相比，IGG III 抗差模型采用分段思想，其具有有界、分段、高效和連續的特性，無論是靜態定位還是動態定位，均表現出更高的應用價值。