L波段雷達高度差報警閾值的研究與建議

沈 曄，徐志剛，馬瑋駿

(1.95871部隊探空教研室，衡陽 421001；2.南京金水尚陽信息技術有限公司，南京 210046)

0 引言

高空氣象探測雷達在探測過程中，可以得到探空儀上升過程中的實時高度，該高度一方面代表氣象要素值所在高度，另一方面作為氣球升速、風向風速、氣球下沉段、球炸時間等的計算參數或參考指標，因此高空氣象探測雷達所探測高度的準確性直接影響高空氣象探測資料的質量[1，2]。

就L波段雷達綜合探測而言，每秒可以得到兩個高度值：一是利用探空儀所采集的溫度、氣壓、濕度數據，通過壓高公式計算出高度值，簡稱氣壓高度；二是基于雷達所測仰角和距離數據，通過三角函數計算1個高度值，簡稱雷達高度[3，4]。氣壓高度與雷達高度本質上都是指探空儀所在高度，然而由于機械誤差、傳感器誤差、計算公式誤差等的存在，這兩個高度與探空儀所在高度的真值存在誤差。業務探測過程中，為了評價這兩個高度與探空儀高度真值的逼近程度，引入了高度差值的概念[5，6]。

當前高空氣象探測業務中，理論上在雷達出現大仰角時，會出現高度差報警閾值過大，失去報警意義；實際探測中，高度差報警閾值在探測中期會出現極大值，即高度差報警閾值并不隨探測高度而單調變化。針對該問題，文章分析了高空氣象探測中雷達高度、氣壓高度以及兩者之間的異同，其次說明了雷達高度差值的來源，并深入探討了高度差值報警的原理，結合實際探測業務分析了高度差報警閾值的應用案例，最后給出了L波段雷達高度差值報警的改進建議。

1 相關定義

1.1 雷達高度

已知地面雷達海拔高度、探空儀與地面雷達的距離(又稱斜距)以及探空儀相對于地面雷達的仰角，通過三角函數可以計算出探空儀距地面雷達所在平面的垂直高度，從而得到探空儀的海拔高度，即通過雷達測量探空儀的海拔高度，簡稱雷達高度。

取極坐標系，如圖1所示，O表示雷達天線(即測站)所在位置，A為探空儀在某一時刻的空間位置，C為探空儀所在空中位置P的水平投影點，δ為OA與OC的夾角，R為探空儀所在空中位置A距測站O的直線距離(即斜距)，ON為正北方向，那么探空儀距測站的垂直高度Z表示為：

Z=R·sinδ

(1)

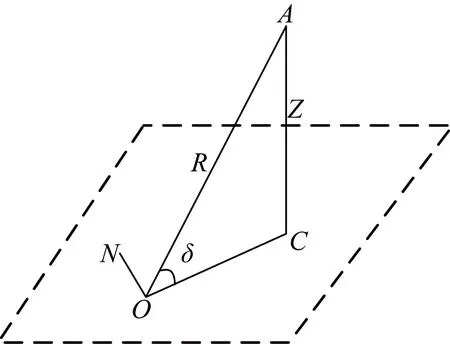
圖1 雷達高度示意圖

假設測站海拔高度為Ho，那么探空儀的海拔高度HA表示為：

HA=Ho+Z=Ho+R·sinδ

(2)

由公式(2)可知，探空儀的海拔高度HA是通過雷達所測得仰角δ、斜距R、測站的海拔高度Ho計算得到，因此HA也稱為探空儀的雷達高度。

公式(2)僅是計算雷達高度的核心公式，在實際應用過程中，需要注意的是：

1)由于大氣折射率的存在，公式(2)中的雷達所測仰角δ與斜距R，均應該進行大氣折射修正；

2)雷達所測斜距R，其量值是幾何長度的“米”，在提供給天氣學和氣候學時，需要轉換為與測站重力加速度相關的位勢高度；

3)探空儀雷達高度是基于雷達天線旋轉中心所在站心坐標平面的，在計算探空儀位勢高度時，需要將其轉換成地心坐標上。

1.2 氣壓高度

根據《常規高空氣象觀測業務規范》中計算位勢高度的公式(即“氣壓-高度公式”，也簡稱“壓高公式”)，可以計算出各相鄰兩氣壓層之間的厚度，將逐層厚度累計，得到的累計厚度，即氣壓高度，計算公式如式(3)所示：

(3)

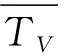
由公式(3)可知，探空儀的氣壓高度是通過計算逐層厚度(通常前后兩組探空數據的厚度為一層)，然后將逐層厚度累加而得，因此在使用過程中需要注意以下幾點：

1)同一位置探空儀，由于探空數據異常、刪除等原因，其氣壓高度可能存在較小偏差；

2)探空儀測得的溫度、濕度也是計算氣壓高度的因子，但對氣壓高度的數值影響較小。

1.3 雷達高度與氣壓高度的異同

1)相同點

①雷達高度和氣壓高度均可以表征探空儀與地面之間的距離；

②雷達高度和氣壓高度均是通過公式間接計算而來，不是直接測量值；

③雷達高度和氣壓高度不一定等于探空儀高度的真值。

2)差異點

①雷達高度是通過幾何公式計算得出，單位：m；而氣壓高度是基于大氣靜力學方程推導而來，其單位是位勢米，因此兩者需要統一量綱后才能對比。

②雷達高度的準確度取決于雷達所測探空儀的方位角、仰角以及雷達與探空儀之間斜距是否準確；而氣壓高度的準確度取決于探空儀所測得的氣壓、溫度和濕度是否準確。

2 高度差值

2.1 高度差值定義

如圖2所示，假設O為雷達天線所在位置，其海平面高度為Ho，某一時刻，雷達所測探空儀的雷達高度的位置為A，氣壓高度位置為B，A、B在水平面上的投影均為C(實際上，空間位置B在水平面上的投影不一定是C，為了便于描述，在保持B高度不變的情況下，將B水平位移到C的垂直上方)，此時斜距|AO|為R(R≥0)，雷達仰角∠AOC為α(0≤α≤90°)，氣壓高度位置的仰角∠BOC為β(0≤β≤90°)，兩者之間的角度差∠BOA的值為γ，其計算公式如下：

(4)

而高度差值的計算公式為：

(5)

圖2 雷達高度差值示意圖

2.2 高度差報警原理

高空氣象探測業務所述雷達高度差大，即公式(5)中ΔH的絕對值大于閾值ΔHmax(ΔHmax>0)，導致放球軟件高度差報警[7]。然而，目前高空氣象探測雷達終端軟件判斷雷達高度差大小是根據夾角γ來判斷的：當|γ|≤1°時，判斷為雷達高度差值正常，終端軟件顯示雷達高度差不報警，而當|γ|>1°時，則認為雷達高度差過大，終端軟件顯示雷達高度差報警。

然而實際工作中，探測人員對γ的閾值并不敏感，也不直觀，因此文章對公式(5)做進一步推導：

(6)

分析公式(6)可知，在高度差值不報警的前提下，當γ取極值-1°或1°時，雷達高度差值ΔH的絕對值也取極值ΔHmax，ΔHmax只與斜距L、仰角α有關，換而言之，報警閾值ΔHmax是一個變量。

為了直觀表示ΔHmax的變化情況，分別給出γ=1°和γ=-1°時，報警閾值ΔHmax隨斜距L、仰角α的變化關系如下：

1)當γ=1°，高度差值ΔH的極值隨著仰角α的增大而增大；

2)當γ=-1°，高度差值ΔH的極值隨著仰角α的增大而減小；

3)隨著仰角α的增大，高度差值ΔH極值增大或減小的幅度越來越大。

特別地，當仰角α≥70°時，報警閾值ΔHmax變化特別大，甚至達到了2000 m以上，報警閾值ΔHmax越大表明高度差值報警條件越寬松，就實際工作而言，以該報警閾值(如大于2000 m)作為判斷雷達高差過大的標準，若ΔHmax過大，則失去了高度差報警的目的。

3 報警閾值應用分析

3.1 資料來源

文章選取邵東氣象臺不同季節的4份探空資料球坐標數據，分析報警閾值在實際應用過程中的變化規律，所選取的探空資料已經通過了質量控制，且終止原因均為球體破裂，4份資料的具體信息如表1所示。

表1 邵東氣象臺所選資料信息

3.2 應用分析

基于表1的4份探測資料，分別計算在探空儀上升過程中的實際仰角、斜距，繪制出高度差報警閾值的變化情況。

通過分析4份資料的報警閾值可知：

1)在整個探測過程中，報警閾值總體呈倒三角形。

2)施放時間越長，探空儀高度越高，報警閾值也越大。這主要是由于高空雷達保持了一個較小的仰角，報警閾值主要隨斜距的增大而逐漸增大。

3)在斜距變化不是特別大的時候，隨著仰角出現先增大后減小的變化趨勢，報警閾值也出現先增大后減小的變化趨勢。

綜上，具體探測業務中，在探空儀上升過程中目前L波段雷達終端軟件的報警閾值并不是單調變化的，而是與實際的仰角和斜距有關。

4 結束語

4.1 報警閾值存在的問題

在高空氣象探測業務中引入高度差，其目的是通過計算兩個高度的非真值(即雷達高度和氣壓高度)之間的逼近度，間接證明雷達高度和氣壓高度的可信度，以確保探空儀高度測量的準確性，然而由于間接計算高度無法避免測量誤差，且當前氣象資料使用者(氣象預報員或保障決策者等)只需要得到符合氣象保障任務的高度準確度值即可，是允許高度存在一定程度的誤差，因此如何將“一定程度的誤差”進行量化，需要進一步探討。

當前L波段雷達終端軟件是通過約束公式(4)中夾角γ的范圍來確保高度測量的準確性，這種方法存在以下3方面問題：

1)理論上，高仰角(如大于70°)時的高度差報警閾值會很大(如大于2000 m)，從而失去報警意義；

2)在實際探測業務中，報警閾值在探測中期會出現極大值，并不隨探空儀高度增大而單調變化；

3)當前高度差報警閾值的設置依據是基于氣壓敏感元件和雷達裝備自身的測量誤差而得，不是根據氣象資料使用者的允許誤差而得，因此這種方法得出的高度差報警閾值與氣象資料使用者能接受的高度差允許閾值不同，從資料應用角度而言，也就不具備參考性。

4.2 建議

《常規高空氣象觀測業務規范》中明確“0～20 min，每1 min為1個計算層風，20～40 min，每隔2 min為1個計算層風，40 min以上，每隔4 min為1個計算層風”，可得出不同施放時間段內計算層風的厚度是不相同的；進一步，在相同的可信度下，計算層風的厚度愈大，表明其可“容忍”的高度偏差也愈大。因此，下一步可以根據不同施放時間段，設置不同的報警閾值，這樣從高度差值的應用角度而言更符合實際需求[8]。